
EFFICIENT 3D DATA COMPRESSION THROUGH
PARAMETERIZATION OF FREE-FORM SURFACE PATCHES
Marcos A. Rodrigues, Alan Robinson and A. Osman
Geometric Modelling and Pattern Recognition Research Group, Sheffield Hallam University, Sheffield, U.K.
Keywords:
3D data compression, Surface parameterization, 3D reconstruction.
Abstract:
This paper presents a new method for 3D data compression based on parameterization of surface patches.
The technique is applied to data that can be defined as single valued functions; this is the case for 3D patches
obtained using standard 3D scanners. The method defines a number of mesh cutting planes and the intersection
of planes on the mesh defines a set of sampling points. These points contain an explicit structure that allows us
to define parametrically both x and y coordinates. The z values are interpolated using high degree polynomials
and results show that compressions over 99% are achieved while preserving the quality of the mesh.
1 INTRODUCTION
Cheap storage and secure transmission of 3D data
bring advantages to a number of applications in se-
curity, engineering, CAD/CAM collaborative design,
medical visualization, entertainment and e-commerce
among others. We have developed and demonstrated
original methods and algorithms for fast 3D scanning
for a number of applications with particular focus on
security (Robinson, 2004), (Brink, 2008), (Rodrigues,
2008), (Rodrigues, 2009). Our algorithms can per-
form 3D reconstruction in 40ms and recognition in
near real-time, in just over one second per subject.
This paper is concerned with compression of 3D
data for fast transmission over the Internet. A re-
alistic scenario we are exploring involves 3D facial
biometric verification at airports. The method is
non-intrusive and aims at minimal disruption and is
based on our past experience with 3D biometrics at
Heathrow Airport (London, UK) in 2005. An enroll-
ment shot is taken and reconstructed in 3D at an au-
tomated check-in desk, where a new database is cre-
ated for each flight. At the gate, before boarding the
plane another 3D shot is taken for verification. The
created databases are transmitted to the local Police
who would perform a search against their records. If
the Police find no information to warrant keeping the
data for longer, all data must be erased after a time
lapse, normally within 24 hours. For international
flights and where no mechanisms for sharing infor-
mation between Police Forces are available, the data
can be transmitted to the destination Police authorities
before the flight actually arrives at the destination.
A significant constraint of this scenario is that 3D
files are very large; a high definition 3D model of a
person’s face is around 20MB. For a flight with 400
passengers, this would mean to dispatch 8GB of data.
If we consider the number of daily flights in a medium
sized airport, we soon conclude that this may be un-
workable. It is clear that methods to compress 3D data
would be beneficial to the scenario considered here
but, more importantly, would represent an enabling
technology for a potential large number of other ap-
plications.
Although some standards exist for 3D compres-
sion such as Java 3D and MPEG4, the compression
rates are still low for general sharing of files over the
Internet. In general there are three methods one can
use to share 3D data. The first method is based on im-
age compression where each snapshot of a 3D scene
is compressed as a 2D image. The second method is
based on hierarchical refinement of a 3D structure for
transmission, where a coarse mesh is followed by in-
creasing refinements until the original, full 3D model
is reconstructed at the other end. The third method
is based on mesh compression where algorithms tra-
verse the mesh for local compression of polygonal re-
lationships.
Compression methods are focused on represent-
ing the connectivity of the vertices in the triangu-
lated mesh. Examples include the Edgebreaker al-
gorithm (Szymczak, 2000) and (Szymczak, 2002).
Products also exist in the market that claim a 95%
lossless file reduction such as from 3D Compression
130
Rodrigues M., Robinson A. and Osman A. (2010).
EFFICIENT 3D DATA COMPRESSION THROUGH PARAMETERIZATION OF FREE-FORM SURFACE PATCHES.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 130-135
Copyright
c
SciTePress

Technologies Inc (3DCT, 2010) for regular geomet-
ric shapes. Other techniques for triangulated models
include the work of (Shikhare, 2002) and vector quan-
tization based methods (Hollinger, 2010) where rates
of over 80:1 have been achieved.
The 3D compression method proposed in this pa-
per was devised from our research on fast 3D acquisi-
tion using light structured methods (Robinson, 2004),
(Rodrigues, 2008), (Brink, 2008), (Rodrigues, 2009).
The 3D scanning method is based on splitting the pro-
jection pattern into light planes. Each plane hits the
target object as a straight line and the apparent bend-
ing of the light due to the position of the camera in
relation to the projection allows us to calculate the
depth of any point along the projected light plane.
Taking full advantage of such properties, our method
is closer to polygonal mesh compression but with sig-
nificant differences as it does not depend on search-
ing for local relationships that are most susceptible to
compression. We have achieved compression rates of
free-form surface patches that drastically reduce the
original 3D data by over 99% to a plain text file. Once
in plain text, it can be encrypted and securely trans-
mitted over the network and reconstructed at the other
end.
This paper is organized as follows. Section 2
presents the method and Section 3 describes the in-
stantiation of the method to surface patches. The data
are compressed and reconstructed and a comparative
analysis of polynomials of various degrees is pro-
vided. Finally a conclusion is presented in Section 4.
2 METHOD
2.1 The Surface Patch as an Explicit
Function of Two Variables
The method presented here applies to surface patches
acquired by standard 3D scanning techniques. Any
such patch can be described as a single valued shape
in one dimension where their values are represented
as an explicit function of two independent variables.
The height of a point is represented by their z-value
and we can say that the height of a function (x, y)
is some function f (x,y). The advantage of a single-
valued function is that it has a simple parametric form,
P(u,v) = (u,v, f (u,v)) (1)
with normal vector n(u, v) = (−δ f /δu, −δ f /δv, 1).
Both u and v are the dependent variables for the func-
tion and u-contours lie in planes of constant x, and
v-contours lie in planes of constant y. When such
patch is visualized in 3D using quads, each edge of
the polygons is a trace of of the surface cut by a plane
with x = k
1
and y = k
2
for some values of k
1
and k
2
.
2.2 Sampling and Reconstruction
Given a randomly oriented surface patch described in
relation to a global coordinate system, it is necessary
to orient the surface using the properties of its bound-
ing box. Geometric algorithms exist to approximate
a minimum bounding box of a 3D object defined by
a set of points, e.g. (Lahanas, 2010). The patch must
be rotated until its minimum bounding box edges are
aligned with the x-, y-, and z-axes of the global coor-
dinate system. Normally, the smallest dimension of
the bounding box is aligned with the z-axis. The pro-
posed method is based on sampling surface points at
the intersection of horizontal and vertical mesh cut-
ting planes.
Horizontal and vertical planes are defined as par-
allel to one of the x or y-axes with normal vectors
(1,0,0) and (0, 1, 0) respectively. The intersection of
any two planes defines a line, and the points where
such lines intersect the mesh are sampled. A problem
here is that we cannot guarantee that the intersection
of two planes on the mesh will rest on a vertex. More
likely, it will intersect somewhere on a polygon’s face
somewhere between vertices. A good approximation
is to find the three vertices on the mesh that are the
nearest to the intersection line. Such vertices define
a plane and it then becomes straightforward to deter-
mine the intersection point. Assume that the line has a
starting point S and direction c. The intersection line
is given by
L(t) = S +ct (2)
The solution only involves finding the intersection
point with the generic plane (Hill, 2001). The generic
plane is the xy-plane or z = 0. The line S + ct inter-
sects the generic plane when S
z
+c
z
t
i
= 0 where t
i
is t
“intersection”:
t
i
= −
S
z
c
z
(3)
From equation (2), the line hits the plane at point P
i
:
P
i
= S − c(
S
z
c
z
) (4)
The vector of all points on the mesh belonging to a
particular plane is a sub-set of the sampled points.
Depending on the characteristics of the surface patch,
either the set of points lying in the horizontal or ver-
tical planes can be selected. If the selected points
lye in planes with normal vector (1,0,0), the distance
between each sampled point is the distance between
planes with normal (0, 1, 0) and vice-versa. Calling
EFFICIENT 3D DATA COMPRESSION THROUGH PARAMETERIZATION OF FREE-FORM SURFACE PATCHES
131

these distances D
1
and D
2
, the x and y coordinates of
any sampled point can be recovered for all planes k:
x
r
= {rD
1
,|r = 1,2,...,k
1
} (5)
y
c
= {cD
2
,|c = 1,2, . . .,k
2
} (6)
where (r, c) are the indices of the planes. This is a
significant outcome of the proposed method, as it is
not necessary to save the actual values (x,y) of each
vertex; instead, only D
1
,D
2
,k
1
and k
2
are kept. This
allows us to discard 2/3 of the data. To illustrate
the compactness of this representation, a mesh with
100,000 vertices means that we have to keep 300,000
values for the set (x, y,z). We instantly eliminated
200,000 values replacing them by 4 numbers only.
We now turn our attention to the z-values. These
can be expressed as in equation (1) as a single valued
function and estimated using equation (4) for each
combination of (x
r
,y
c
). If we choose to represent
these as the set of points belonging to planes with
normal (1, 0, 0) this is reduced to a 2D case in which
on the horizontal axis we have exactly k
2
points with
constant step of D
2
and on the vertical axis we have
their corresponding z-values. This can be expressed
as an n-th-degree polynomial in z
a
0
+ a
1
z + a
2
z
2
+ · · · + a
n
z
n
(7)
A high degree polynomial fitting is performed on each
of such curves using the z-values as “control points”.
The desired outcome is a polynomial that passes ex-
actly through each control point. The coefficients of
the polynomial are saved for each curve together with
the indices of the k planes for the first and last valid
vertices. This is so because we may have several
plane intersections that do not intersect the mesh and
such combination of indices (k
r
,k
c
) must be marked
as invalid vertices.
The reduction in data is substantial: using the ear-
lier example of 100,000 vertices, if we cut the mesh
with 100 planes we need to keep a set of 100 polyno-
mial coefficients together with the first and last valid
vertex indices. Assuming that we are using a polyno-
mial of degree 25, we need to keep 28 numbers for
each plane: 26 coefficients plus 2 vertex indices. This
is a reduction from 100,000 to 2,800 numbers. To re-
construct the original mesh, the polynomials used in
equation (7) are evaluated for each plane within their
boundaries (first and last valid vertices), and the (x,y)
values are evaluated for each combination of (r,c)
plane indices through equations (5) and (6).
3 RESULTS
In this section we describe a step by step application
of the method described in Section 2 with compara-
tive analysis of interpolation using various high de-
gree polynomials.
3.1 Data Compression
The steps and the parameters used for data compres-
sion are as follows.
1. A given triangulated surface patch acquired using
a structured light scanner is aligned to the global
coordinate system where the smallest dimension
of its bounding box is aligned with the z-axis (Fig-
ure 1).
2. A number k
1
of horizontal planes with normal n =
(1,0, 0)
T
cut the mesh as shown in Figure 2 (only
3 planes are shown). These planes are parallel to
the Y-Z plane of the coordinate system in Figure
1.
3. A number k
2
of vertical planes with normal n =
(0,1, 0)
T
cut the mesh as shown in Figure 3 (only
3 planes are shown). These planes are parallel to
the X-Z plane of the coordinate system.
4. The intersection of each plane k
r
with plane k
c
de-
fines a line. For each line determine the point P
r,c
where the line intersects the mesh through equa-
tion (4). These are the heights of the single-valued
function.
5. For each plane k
r
,k
c
make a list of the intersection
points P
r,c
.
6. The distance between each horizontal plane is de-
fined as a constant D
1
and the distance between
vertical planes is defined as a constant D
2
.
7. Perform polynomial interpolation and save the co-
efficients and the plane indices of the first and last
valid points.
Figure 1: Original 3D mesh with 48,672 vertices and 78,043
faces. The size of the file (OBJ format) is 4.83MB with
texture mapping and 4.0MB with no texture.
Figure 4 depicts the intersection of all horizontal
and vertical planes where each intersection is marked
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
132

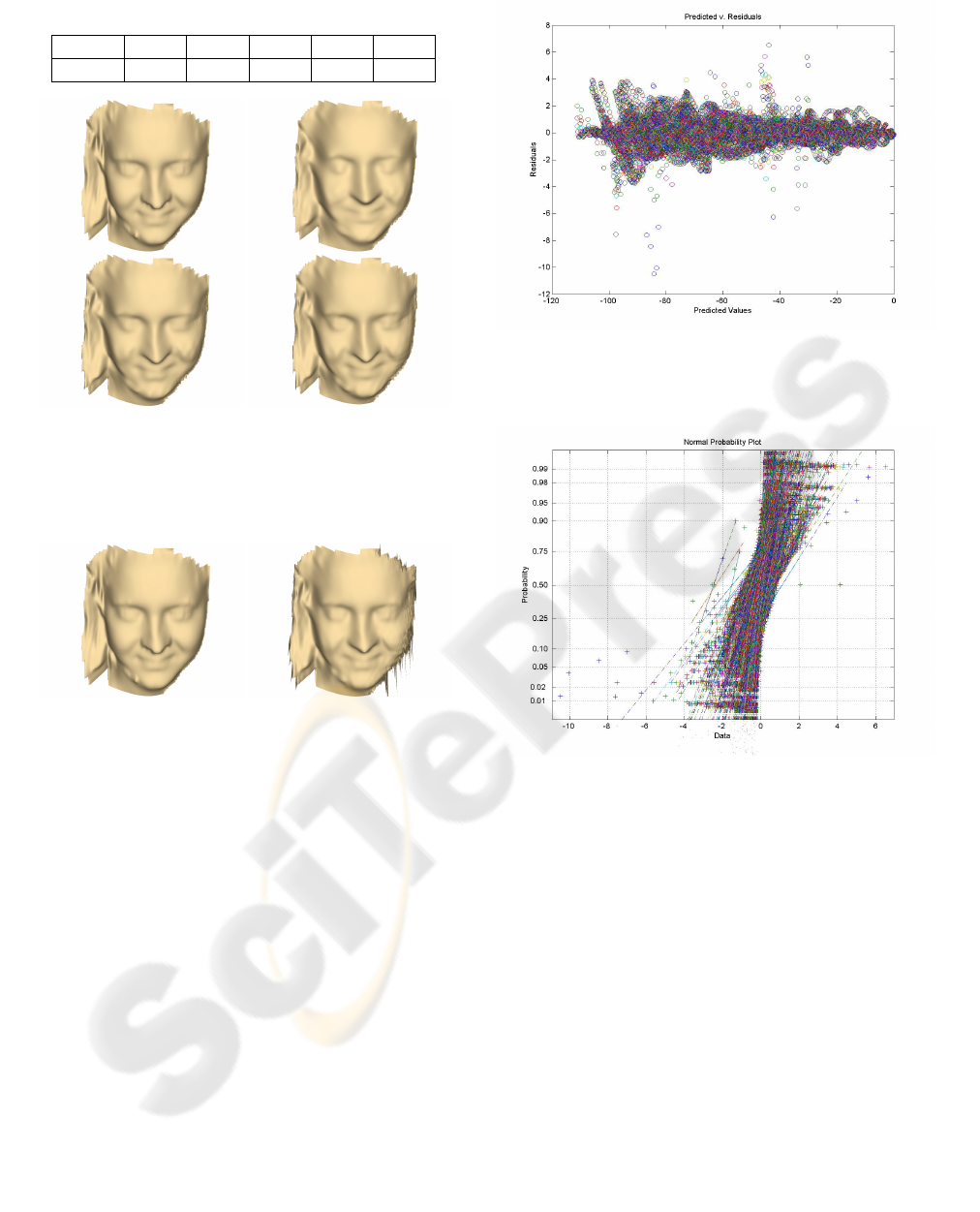
Table 1: Compression rates in percentage.
Degree 20 30 40 50 80
Rate 99.35 99.07 98.79 98.53 97.66
Figure 5: Top row: the original face model is shown on the
left with file size of 4MB; right, with polynomial interpo-
lation of degree 20 reducing the file size to 26KB. Bottom
row: left, polynomial interpolation of degree 30 reducing
the file size to 37.2KB; right, degree 40 reducing to 48.5KB.
Figure 6: Left, the original face model; right, interpolation
with polynomial degree 80. It is noted that the model be-
comes unstable.
3.3 Evaluating the Fit
Determining the quality of a polynomial regression or
how well the recovered data points fit the original data
can involve a number of tests including statistics sum-
maries. By far the most meaningful way is by plotting
the original and regression data sets and visually as-
sess its quality. By visually analyzing the models of
Figure 5, it is suggested that a polynomial interpola-
tion of degrees 20 to 40 describes well the data and
can be well-suited for most applications.
Another way of assessing quality is to look at the
residuals and plot them against the predicted values.
Figure 7 shows the plot for data interpolated with a
polynomial of degree 30. For a good fit, the plot
should display no patterns and no trends. The scatter
plot shows what looks like random noise which is a
good measure of the quality of the fit. Alternatively, if
the fit is good, a normal-probability plot of the resid-
Figure 7: Scatter plot of Predicted Values against Residuals.
For a good fit, it should show no patterns and no trends. The
plot shows what looks like random noise indicating a good
fit.
Figure 8: The normal-probability plot of the residuals. A
good fit should describe a straight line for each polynomial
curve which is verified by the plot indicating a good fit.
uals should display a straight line. The plot depicted
in Figure 8 shows that for most polynomials evalu-
ated at each plane, indeed they describe a straight line
indicating a good fit.
There are a number of statistical measures to as-
sess the quality or the appropriateness of a model such
as the coefficient of determination also known as R
2
that indicates the percent of the variation in the data
that is explained by the model. This can be estimated
by first calculating the deviation of the original data
set which gives a measure of the spread. While the to-
tal variation to be accounted for (SST) is given by the
sum of deviation squared, the variation that is not ac-
counted for is the sum of the residuals squared (SSE).
The variation in the data explained by the model is
given by
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
134

R
2
= 1 −
SSE
SST
(8)
expressed as percentage. The R
2
values for some in-
terpolated models are described in Table 2. The ta-
ble shows a trend of increasing R
2
as the polynomial
degree increases, peaking at around degree 30. For
higher degrees, R
2
decreases monotonically, and this
is also confirmed by visual inspection of the 3D re-
constructed models whose quality deteriorates as they
become unstable for high degree polynomials.
Table 2: The coefficients of determination R
2
for polyno-
mial fits of degrees 20–80 for the given data.
Degree 20 30 40 50 80
R
2
0.9995 0.9996 0.9995 0.9994 0.9909
4 CONCLUSIONS
We have presented a new method of data compres-
sion applied to surface patches that can be defined as a
single valued function. This is the case of 3D data ac-
quired using standard 3D scanning technologies. The
method was described based on mesh cutting planes
oriented with the global coordinate system with con-
stant step. The points where the plane intersections
intersect the mesh are sampled and this automatically
allows the recovery of all (x, y) coordinates for all
vertices. The z-values are subject to polynomial in-
terpolation of various degrees. Results demonstrate
that the method is effective and can reduce the mesh
over 99%. Both close visual inspection and statisti-
cal measures demonstrate that optimal performance is
achieved for polynomials of degree between 20 to 40
– it seems that the optimal value is around 30, but this
obviously depends on the characteristics of the data.
There seems to be intrinsic limitations using poly-
nomials to approximate complex real world surface
patches. In the future we will investigate the use of
splines as it is possible to get more accurate results
than with polynomials but the price we pay is that it
will generate larger files as we need to keep the coef-
ficients of all polynomials between the control points.
A more promising approach is to investigate the use of
PDEs and research is under way and will be reported
in the near future.
REFERENCES
3DCT (2010). 3D Compression Technologies Inc. available
at http://www.3dcompress.com/web/default.asp
Brink, W., A. Robinson, and M. Rodrigues (2008). Indexing
Uncoded Stripe Patterns in Structured Light Systems
by Maximum Spanning Trees, British Machine Vision
Conference BMVC 2008, Leeds, UK, 1–4 Sep 2008
Hill, F. S. Jr (2001). Computer Graphics Using OpenGL,
2nd edition, Prentice-Hall Inc, 922pp.
Hollinger, S. Q., A. B. Williams, and D. Manak (2010).
3D data compression of hyperspectral imagery using
vectorquantization with NDVI-based multiple code-
books, available at http://sciencestage.com
Lahanas, M. (2010). Optimal Oriented Bounding Boxes,
http://www.mlahanas.de/CompGeom/opt bbox.htm,
last accessed April 2010.
Rodrigues, M. A. and A. Robinson (2010). Novel Methods
for Real-Time 3D Face Recognition, 6th Annual In-
ternational Conference on Computer Science and In-
formation Systems, 25–28 June 2009, Athens, Greece.
Rodrigues, M. A., A. Robinson, and W. Brink (2008). Fast
3D Reconstruction and Recognition, in New Aspects
of Signal Processing, Computational Geometry and
Artificial Vision, 8th WSEAS ISCGAV, Rhodes, 2008,
p15–21.
Robinson, A., L. Alboul and M. A. Rodrigues (2004). Meth-
ods for Indexing Stripes in Uncoded Structured Light
Scanning Systems, Journal of WSCG, 12(3), 2004, pp
371–378.
Szymczak, A., D. King and J. Rossignac (2000). An
Edgebreaker-Based Efficient Compression Scheme
for Regular Meshes, 12th Canadian Conference on
Computational Geometry, pp 257–265.
Szymczak, A., J. Rossignac, and D. King (2002), Piecewise
Regular Meshes, Graphical Models 64(3-4), 2002,
183–198.
Shikhare, D., S. V. Babji, and S. P. Mudur (2002). Com-
pression techniques for distributed use of 3D data: an
emerging media type on the internet, 15th interna-
tional conference on Computer communication, India,
pp 676–696.
EFFICIENT 3D DATA COMPRESSION THROUGH PARAMETERIZATION OF FREE-FORM SURFACE PATCHES
135
