Computation Independent Models: Bridging Problem

and Solution Domains

Erika Asnina and Janis Osis

Department of Applied Computer Science, Institute of Applied Computer Systems

Faculty of Computer Science and Information Technology, Riga Technical University

LV-1048, Riga, Latvia

Abstract. Compliance between a problem and a solution domain(s) is a well-

known issue in software development. A usual way of development is focusing

on the solution, and adapting the solution to the problem domain only in case of

occurred issues. Sometimes, the cost of such adaptation is very high, and then

the cheapest way is to change operation of the problem domain. Certainly, such

ways cannot satisfy a client. This paper considers a computation independent

model as a place where overcoming of the gap must occur. It discusses ways for

overcoming a gap between a problem domain and a solution domain(s) that are

proposed within CIMs, and suggests a mathematical mechanism, continuous

mapping, provided by a topological functioning model together with its other

topological and functional properties as a formal bridge between those domains.

This mechanism is explained by an example.

1 Introduction

Software development begins from analyzing a problem and finding a solution or

solutions. In practice, developers design the solution without proper investigation of

the problem as they consider that the required solution is this problem mentioned.

Therefore, the question about what domain must be modeled at first, the domain of

today reality (“system-as-is”) or the domain of customer expected reality (“system-to-

be”), still is open.

The answer on this question is not new. [17] pointed out that the first step should

be evaluating of client’s current situation, and only after that developers should define

what the new product will be able to do. He stated that the primary goal of the

requirement phase is to notify what client needs. The same thought is repeated in [19]

and Jackson’s work [9] at problem frames used for problem analysis. System

requirements themselves are only constraints hung on real world phenomena, not vice

versa [15].

There are two ways of problem domain analysis. The first one is when developers

explore the problem domain by parts, at the beginning trying to understand each

fragment of the problem domain and only after that trying to join those fragments

together in the joined and more formal representation. The second one is the so called

system thinking, where the problem is analyzed at the whole, and only then its

fragments are separated and refined.

Asnina E. and Osis J. (2010).

Computation Independent Models: Bridging Problem and Solution Domains.

In Proceedings of the 2nd International Workshop on Model-Driven Architecture and Modeling Theory-Driven Development, pages 23-32

DOI: 10.5220/0003043200230032

 SciTePress

In both cases mappings between the problem domain and the solution (or

solutions) must be determined. System thinking facilitates this issue as the problem

domain is analyzed the first, and the solution is defined in accordance with the

understood problem. Unfortunately, there is a lack of formal ways to map knowledge

about the problem domain into the software development process. However, if we

develop this software for some purposes in the real world, we must know how it will

affect it. It has critical importance for business, mechatronic and embedded systems,

where the cost of the fail could be human lives or vast damages.

Object Management Group’s Model Driven Architecture proposes three models for

system specification, namely, a Computation Independent Model (CIM), a Platform

Independent Model (PIM), and a Platform Specific Model (PSM). PIMs and PSMs

are dedicated for specification of solutions, i.e., systems-to-be. This paper will discuss

the first model mentioned, the CIM, where the specification domain (domains) is not

so explicit. The CIM describes system requirements and the way the system works

within its environment. Details of the application structure and realization are

assumed to be hidden or as yet undetermined. The CIM is sometimes called a domain

model and a domain vocabulary. However, domains that can be reflected by CIMs are

not clearly stated in the specification of MDA [12].

In broad sense we may assume that both problem domain and solution domain can

be specified by the computation independent model. And this assumption is correct as

it will be shown in this paper. Thus, it is interesting to understand where and how this

“gap” between the problem domain and the solution domain can be overcome and by

what means.

The paper is organized as follows. Section 2 overviews other authors’ research on

CIMs, and analyzes ways of the gap overcoming. Section 3 introduces a formal

holistic CIM, i.e., a Topological Functioning Model (TFM) in brief. Section 4

discusses a formal mechanism provided by the TFM and illustrated by an example for

overcoming the gap mentioned above. Conclusion summarizes main results of the

research.

2 Computation Independent Models

By analyzing scientific publications described below, we have recognized that

scientists distinguish three parts or layers within the CIM, namely, CIM – Knowledge

Model, CIM – Business Model, and CIM – Business Requirements for the System.

Let us consider those proposed models in more detail.

The idea of CIM–Knowledge Model proposed by [5] relates to the highest level of

the CIM model levels. This model reflects an enterprise from the holistic point of

view, thus providing the general vision of the enterprise with focus on enterprise

knowledge. The CIM–Knowledge Model may include three types of diagrams,

namely, block, ontological and knowledge diagrams.

Che, Wang, Wen and Ren [3] proposed the similar viewpoint on this level, but they

called this model by Global Model. It describes function requirements of every

enterprise domain and information transmission relationships between those

requirements as well as the whole business logic and information transmission

relationships, based on which CIMs at the detailed levels could be composed. Jeary,

Fouad and Phalp [10] discussed a pre-CIM level, where business managers can create

informal models of department processes. The pre-CIM may include organizational

hierarchies, informal documentation, private process views, details of responsibilities,

any requirements relevant information, very informal concept models, etc. In other

words, the pre-CIM should hold business domain knowledge, while CIMs holds

business process models, and only after that requirements are defined. Garrido,

Noguera, González, Hurtado and Rodríguez [4] presented ontology-based CIMs.

The idea of CIM–Business Model proposed by Grangel et al.[5] and Hendryx, [6]

is a “pure” business model that is focused on the business scope and goals as well as

terminology, resources, facts, roles, policies, rules, organizations, locations and events

of concern to the business. However, it does not reflect system considerations. The

scope of the Business Model in the CIM must, at a minimum, include business

functions served by the system.

Authors in Grangel et al., Kanyaru, Coles, Jeary and Phalp [5, 11], and Garrido et

al., [4] defined three possible types of models within the CIM–Business Model. The

Organizational Model can be described in terms of goals, organizational structure,

analysis diagrams and business rule diagrams. The Structural Model includes product

and resource diagrams, and the Behavior Model includes process and service

diagrams. Authors in [8] refined them to Organization Model, Process Model, Data

Model, System Model, and Service Model. In essence, these models also can be

reduced to those three models described previously.

The CIM–Business Requirements for the System proposed in [6] contains the

contract between the business and IT about what the business people expect the IS

will automate. This model is built on and refers to the CIM–Business Model. Authors

in [7] and [18] stated that in case of ISs each requirement is a system’s obligation to

execute a business rule or rules. Hence, requirements for the system must be in

consistency with the environment where they will be implemented and as complete as

possible. Cao, Miao and Chen [2] proposed a use of feature models for developing

CIMs. In turn, Trujillo, Soler, Fernández-Medina and Piattini [20] proposed the CIM

for requirements analysis for data warehouse modeling based on an extension of the i

framework that deals only with functional requirements at the business level.

2.1 Overcoming the “Gap” between the Problem and Solution

There are two possible kinds of representing systems. The first and wide-used is

fragmental representation. This means that in order to overcome complexity of the

system under consideration, developers divide specification of the system from a

certain viewpoint into several fragments as in case of use cases, where multiple use

cases (fragments) and intuitively and weakly defined dependencies among them

constitute this entire view on the system.

The second kind is holistic representation. Holistic representation may be

described either as a single indivisible (or formally refined) model or as a view on the

system on the whole from different aspects. The latter means that there are formally

defined dependencies among elements in aspects.

We believe that only holistic models are able to overcome the gap between the

problem domain and solution domains completely. Moreover, such models must be

able to represent both domains in order to formally define relationships among them.

In order to overcome the gap between the problem domain and solution domains,

requirements must be in conformity with a business model that describes the problem

domain. The assisting model should be a business model that specifies the solution

domain and is composed in accordance with compliant requirements and reality

specified in the business model of the problem domain. In most of the propositions

discussed business requirements are stated in accordance with the business model that

reflects the solution domain.

Propositions in [5, 10], and [8] have a relation with the business model of the

problem domain. In [5] this relation is obtained by selecting those business functions

from the “pure” business model of the problem domain that are to be served by the

system, and composing corresponding structural and behavioural models. In [10] this

relating node is the business process model of the problem domain that is created

based on the Pre-CIM (an informal model of business processes, organizational

hierachies, informal documentation and very informal concept model) and on which

business reqirements for the system are grounded. In [8] the joining element is the

business context and business requirements for the enterprise integration system. This

context defines existing organization, services, processes and datas, and specifies

requirements for the integration system.

Summarizing, the proposed ways of overcoming the gap mentioned before are

rather intuitive then formal. Even if functions of the solution domain are obtained by

selection from functions of the problem domain, it is not clear how new functions

must be handled in order to keep conformity among two domains or how exclusion of

problem domain functions in the solution domain will affect enterprise operation.

In our paper we present the Topological Functioning Model (TFM), which is a

formal mathematical model for holistic (single indivisible) representation of both

problem and solution domains and provides a mathematical mechanism for

overcoming the gap between a problem and a solution.

3 The Formal Holistic CIM - Business Model: Topological

Functioning Model

A Topological Functioning Model (TFM) is developed at Riga Technical University

by Janis Osis [13]. The topological model of problem domain is the advantage for

analysis and decomposition of complex systems as described in [14].

The TFM is a mathematically formal model that describes a topology among

systems functional properties from the computation independent viewpoint. It is

independent of any modeling and implementation technique. It comes about through

the acquisition of the experts' knowledge about the complex system, verbal

description, and other documents concerning the structure and functioning.

TFM formalism is based on assumption that a complex system can be described in

abstract terms as a topological space (X, Q), where X is a finite set of functional

features and Q is a topology, given in the form of a digraph (oriented graph).

A functional feature is a characteristic of the system (in its general sense) that is

designed for achieving some system’s goal. The functional features are activities that

help the system to realize its functionality. These activities can be considered as

(specialized) functional features [13], i.e., functional features, whose further

expansion is not necessary at this stage. Functional features can be joined in a

functional feature set, representing a certain business function. Therefore, a set of

specialized functional features can be correlated with the appropriate business

function and corresponding business process.

Cause-and-effect relations among functional features (or topology) must be set. It

is assumed that a cause-and-effect relation between two functional features of the

system exists if the appearance of one feature is caused by the appearance of the other

feature without participation of any third (intermediary) feature.

The TFM has topological and functional properties [13]. The topological properties

are connectedness, closure, neighborhood and continuous mapping. The functional

properties are cause-effect relations, cycle structure, inputs and outputs.

4 Continuous Mapping: The Bridge between Problem Domain and

Solution Domain Models

This paper highlights one of TFM topological properties, namely, continuous

mapping, which together with other TFM topological and functional properties allows

overcoming the gap between the problem and solution.

Fig. 1 illustrates a use of the topological functioning model in software

development. First, a model of the problem domain is constructed by analyzing

knowledge of the system-as-is. Simultaneously client’s requirements (or desires) are

gathered. They are checked up for compliance with the constructed TFM and mapped

onto its functional features. The result is a topological functioning model of the

solution domain that implements continuous mapping into the TFM of the problem

domain. However, we should note that this is a model of the solution domain at the

business level not at the application level. The application level is specified in the

CIM – Business Requirements for the System that is a behavior model in this case.

4.1 Mathematical Foundations of the Continuous Mapping

According to the statement and corollaries of continuous mapping defined in [13], the

model with any complexity can be abstracted to the simpler one and vice verse. This

means that continuous mapping of topological models is realized. Continuous

mapping states that direction of topological model arcs must be kept as in a refined as

in a simplified model. Moreover, a lack of knowledge about the system can be filled

up with knowledge that is obtained from the continuous mapping of the same type

model to the system model under consideration.

Statement: If some more detailed functioning system is formed by substitution of a

subset of specialized properties for some functional property, then continuous

mapping exists between a detailed model and a simplified parent topological model of

the same system.

Proof: The continuous mapping of the topological space of the detailed system T*

into the topological space of the simple parent system T will take place, if

neighborhoods of T* will map into neighborhoods of T.

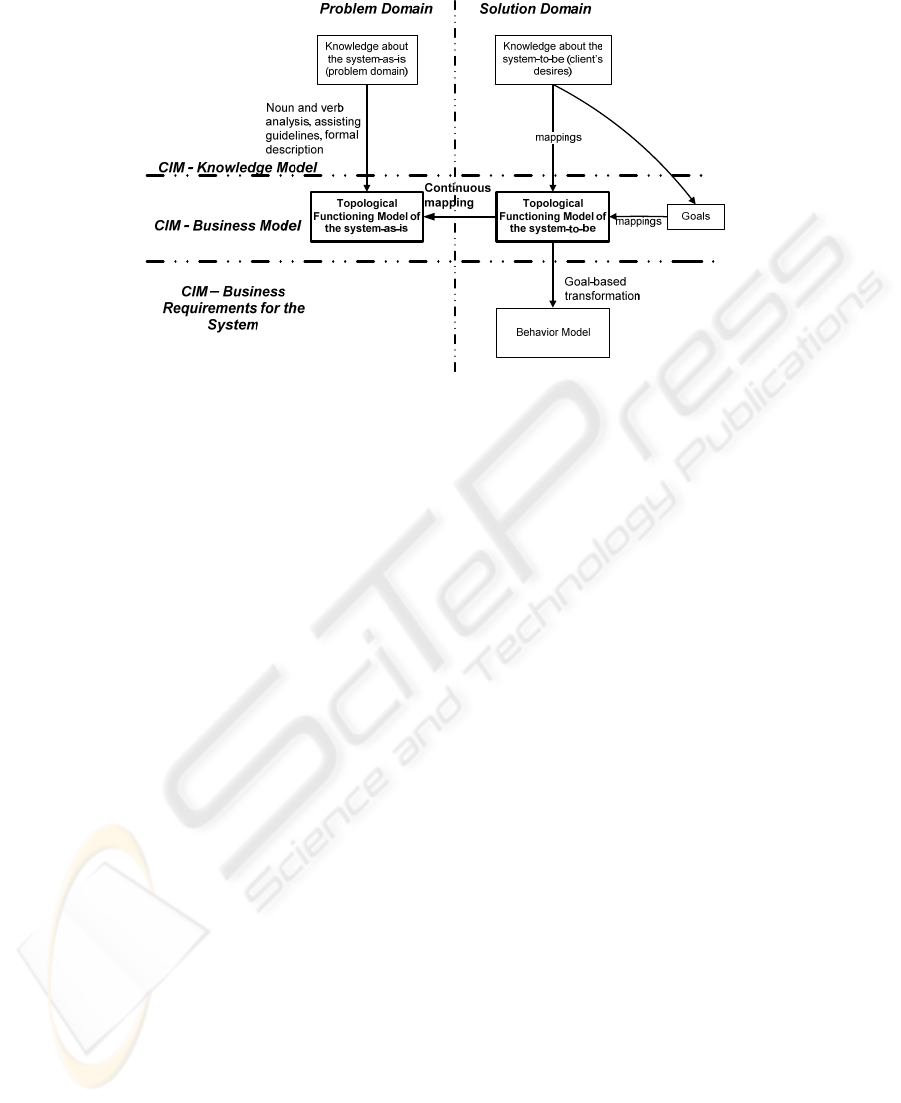
Fig. 1. The place of the topological functioning model in software development.

Let us assume that the contrary is the case, i.e., that neighborhoods of T* are not

mapped into neighborhoods of T. This means that T* possesses other essential

topological properties. Therefore, either the mode of functioning of the detailed

system will be different, or the detailed system will cease to exist at all. It follows that

new essential functional features are being added but it contradicts to the premise of

the statement. It’s easy to prove also the converse statement.

4.2 Discussion

Let us explain and demonstrate the theoretical foundations mentioned above by an

example of a library.

Let us assume that we have the following description of the problem domain, i.e. a

fragment of operation “as is” of this small enterprise: “The library invites people to

come. The Advertising Company gives the informational support for the library.

When a reader comes, he is serviced by a librarian. Each month and after taking back

the librarian evaluates the condition of used prints. If a print is damaged, then it is

either restored by the Restoration Company or removed by the Liquidating Company.

The removed prints are liquidated by the Liquidating Company, while the library

continues to use the restored prints. Library’s Fund Company gives the financial

support that is based on annual library’s reports. The Library’s Fund Company itself

is credited by its partners. Library’s fund gets this financial support. The library

distribute the obtained income among paying salaries to employees, restoring prints,

removing damaged prints and purchasing prints. Each three months the library

purchases prints which are published by publishing houses in order to service their

readers. Before each purchase, the library evaluates readers’ requirements as well the

condition of library’s prints. The library gives the information support by fee.”

The topological functioning model of this library illustrated in Fig. 2-a is

constructed in accordance with a method that is described in detail in [16].

Description of functional features that is a simplified form of the description in [1] is

the following <label: name, preconditions, postconditions>: a: Publishing a print; b:

Coming a reader; c: Purchasing a print; d: Servicing a reader, postcondition

“income”; e: Evaluating the condition of a print, precondition “each month and after

tacking back a print”, postcondition “damaged OR undamaged condition”; f:

Evaluating the requirements of a reader, postcondition “reader’s requirements”; g:

Restoring a print, precondition “if a print is damaged”; h: Distributing income; i:

Removing a damaged print, precondition “if a print is damaged”; j: Giving financial

support, precondition “if it is a review of library’s annual report”, postcondition

“income”; k: Paying the salary to an employee; l: Giving informational support; m:

Creating a report, precondition “if it is a deadline of annual report submission”; o:

Inviting a man; and p: Crediting library’s fund company

Let us assume that a client wants to receive an information system (IS) that

supports functions dedicated to servicing readers, i.e. the following functional

requirements for the IS are set - F1: The system shall provide servicing readers

(functional feature d); F2: The system shall provide evaluating print conditions

(functional feature e); F3: The system shall provide restoring a print (functional

feature g); and F4: The system shall provide paying for print damages.

Here, F1 completely corresponds to functional feature “d: Servicing a reader,

postcondition {income}”; F2 completely corresponds to functional feature “e:

Evaluating the condition of a print, precondition {each month}, postcondition

{damaged OR undamaged condition}”; and F3 completely corresponds to functional

feature “g: Restoring a print, precondition {if a print is damaged}”.

In turn, F4 does not correspond to any existing functional feature in the TFM of the

problem domain. This means that this requirement will introduce new functionality as

in the solution domain (the IS itself) as in the problem domain (operation of the

library as an enterprise). This case requires careful investigation of cause and effect

relations among the existing functional features in the problem domain and this new

one.

In order to introduce this new function into the TFM of the problem domain, we

have created new functional feature “r: Paying for the damage of a print, precondition

{if a print is damaged}”. By analyzing existing functionality, we can assume that the

cause is functional feature e, and an effect is functional feature d. If the cause is

evident, then the effect is implicitly stated. We may assume that if a reader has not

paid for damages done, then he/she will not be able to get library’s services next time

(Fig. 2-b).

The IS to be implemented is a subsystem of the library system. Hence, we can

separate the topological functioning model of the IS from the model of the library.

Accordingly to the rules of separation of the topological model from the topological

space that is illustrated in detail in [16], after the closuring operation we have

obtained the topological functioning model of library’s IS (Fig. 2-c).

Functionality described by functional features d, e, and g that are specified for

implementation already exists in the library as an enterprise (Fig. 2-a). But the

function that supports paying for damaged prints and that will be implemented in the

IS modifies operation of this enterprise by introducing this new responsibility,

functional feature r, as it is shown in the TFM in Fig. 2-b and Fig. 2-c.

Continuous mapping from the TFM of the information system to the TFM of the

library with the IS (“to be”) to the TFM if the library without the IS (“as is”) is

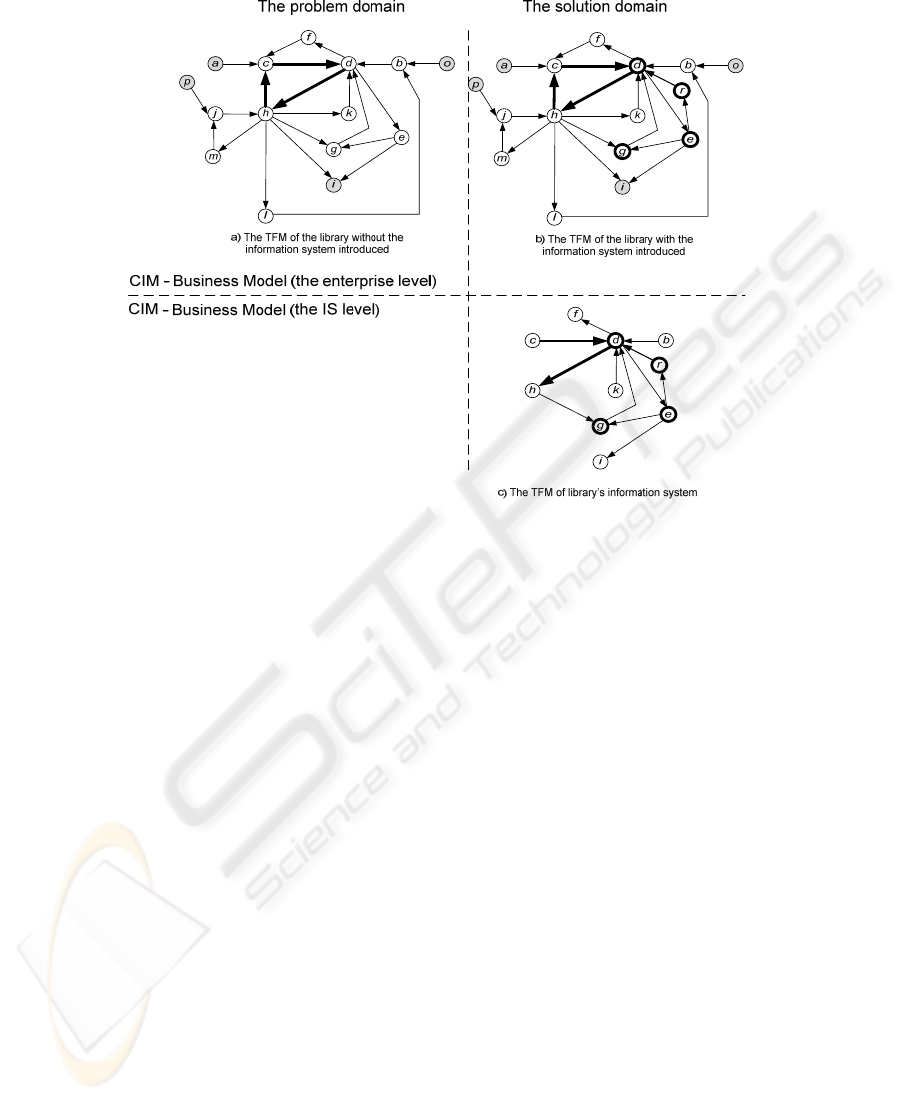
Fig. 2. The topological functioning model of the library in the problem domain without IS’s

support (a), with support of the IS (b), and library’s IS in the solution domain (c).

mathematically proved by mappings of the neighborhoods of the system functional

features, where X

** is a neighborhood of the functional feature of the IS (Fig. 2-c),

* is a neighborhood of the functional feature of the library with the IS (Fig. 2-b),

and X

is a neighborhood of the functional feature of the library without the IS (Fig. 2-

a):

X**

={b, d} → X*

={b, d} → X

={b, d}

X**

={c, d} → X*

={c, d} → X

={c, d}

X**

={d, f, h, e} → X*

={d, f, h, e} → X

={d, f, h, e}

X**

={e, r, i, g} → X*

={e, r, i, g} → X

={e, i, g}

X**

={h, g} → X*

={h, g, k, c, i, l, m} →X

={h, g, k, c, i, l, m}

X**

={g, d} → X*

={g, d} → X

={g, d}

X**

={k, d} → X*

={k, d} → X

={k, d}

X**

={r, d} → X*

={r, d} → Ø

The mappings between the neighborhoods explicitly demonstrate that functional

feature r is not continuously mapped to the initial TFM of the library (the system “as

is”), because it is a new function for the library. However, it is continuously mapped

from the model of the information system to the modified TFM of the library, thus the

solution is in compliance with the problem domain.

5 Conclusions

Discovering gaps between the problem domain and the solution domain is an open

issue in software development. The CIM is the only model within model-driven

development that can specify both these domains and should show such issues

explicitly. Analysis of the existing proposition of CIMs shown that even if both

domains are modeled in the CIM, the relation among them is rather intuitive then

formally defined and specified. This is a cause of future issues with solution’s

inadequacy to the enterprise operation.

This paper illustrated the mathematical mechanism for such inadequacy

identification and handling. The mechanism is TFM topological and functional

properties that support continuous mapping between the system and its subsystems,

and the system and its modifications. Discovered gaps between domains are explicit

and mathematically proved, and possible changes in the system functionality are done

taking onto account already existing interrelationships among system functions. This

mechanism is planned to be implemented in the modeling tool to be developed.

References

1. Asnina, E. (2006). The Formal Approach to Problem Domain Modelling Within Model

Driven Architecture. Proceedings of the 9th International Conference “ISs Implementation

and Modelling” (ISIM’06), April 25-26, 2006, Přerov, Czech Republic, 1st edn. (pp. 97-

104). Ostrava: Jan Štefan MARQ.

2. Cao, X.-x., Miao, H.-k. and Chen, Y.-h. (2008). Transformation from computation

independent model to platform independent model with pattern. Journal of Shanghai

University (English Edition) , 12(6), 515-523.

3. Che, Y., Wang, G., Wen, X. and Ren, B. (2009). Research on Computational Independent

Model in the Enterprise IS Development Mode Based on Model Driven and Software

Component. International Conference on Interoperability for Enterprise Software and

Applications China, 2009. IESA '09. (pp. 85 - 89). IEEE.

4. Garrido, J. L., Noguera, M., González, M., Hurtado, M. V. and Rodríguez, M. L. (2006).

Definition and use of Computation Independent Models in an MDA-based groupware

development process. Science of Computer Programming, 66(1), Special Issue on the 5th

International Workshop on System/Software Architectures (IWSSA’06) (pp. 25-43).

Elsevier B.V.

5. Grangel, R., Chalmeta, R. and Campos, C. (2007). Using UML Profiles for Enterprise

Knowledge Modelling. Proceedings of the 26th International Conference on Conceptual

Modeling (ER 2007), the 3rd International Workshop on Foundations and Practices of

UML (FP-UML 2007), LNCS, Computer Science, Theory & Methods (pp. 125-132). Berlin:

Springer Verlag.

6. Hendryx, S. (2003). Integrating Computation Independent Business Modeling Languages

into the MDA with UML 2. Retrieved from: http://www.omg.org/docs/ad/03-01-32.doc

7. Hendryx, S. (2005, September). Are System Requirements Business Rules? Retrieved from

Business Rules Journal, 6(9). Retrieved from: http://www.BRCommunity.com/a2005/

b249.html

8. Huang, S. and Fan, Y. (2007). Model Driven and Service Oriented Enterprise Integration -

The Method, Framework and Platform. Proceedings of the Sixth International Conference

on Advanced Language Processing and Web Information Technology (ALPIT 2007) (pp.

504-509). Washington, DC, USA: IEEE Computer Society.

9. Jackson, M. (2005). Problem Frames and Software Engineering. The Open University.

Retrieved (n.d.) from: http://mcs.open.ac.uk/mj665/PFrame7.pdf

10. Jeary, S., Fouad, A. and Phalp, K. (2008, July 3). Extending the Model Driven Architecture

with a pre-CIM level. Proceedings of the 1st International Workshop on Business Support

for MDA co-located with TOOLS EUROPE 2008. Retrieved from:

http://ftp.informatik.rwth-aachen.de/Publications/CEUR-WS/Vol-376/

11. Kanyaru, J. M., Coles, M., Jeary, S. and Phalp, K. (2008, July 3). Using visualisation to

elicit domain information as part of the Model Driven Architecture (MDA) approach.

Proceedings of the 1st International Workshop on Business Support for MDA co-located

with TOOLS EUROPE 2008. Retrieved from: http://ftp.informatik.rwth-

aachen.de/Publications/CEUR-WS/Vol-376/

12. Miller, J. and Mukerji, J. (2001). Model Driven Architecture (MDA). Architecture Board

ORMSC, ormsc/2001-07-01. The OMG. Retrieved from: www.omg.org/mda/

13. Osis, J. (1969). Topological Model of System Functioning (in Russian). Automatics and

Computer Science, J. of Acad. of Sc, Riga, Latvia, #6 , 44-50.

14. Osis, J. (1997). Development of Object-Oriented Methods for Hybrid System Analysis and

Design. Proc. of the 23rd Conference of the Association of Simula Users (ASU), (pp. 162-

170). Stara Lesna, Slovakia.

15. Osis, J. (2004). Software Development with Topological Model in the Framework of MDA.

In: Proceedings of the 9

CaiSE/IFIP8.1/EUNO International Workshop on Evaluation of

Modeling Methods in Systems Analysis and Design (EMMSAD’2004) in connection with

the CaiSE’2004 (Vol. 1, pp. 211-220). Riga: RTU.

16. Osis, J., Asnina, E., and Grave, A. (2008). Formal Problem Domain Modeling within

MDA. In: Communications in Computer and Information Science (CCIS) (Vol. 22 (III), pp.

387-398). Berlin: Springer Verlag.

17. Schach, St. R. (1999). Classical and Object-Oriented Software Engineering with UML and

Java. International edition. 4

edn. WCB/McGraw-Hill.

18. Sowa, J. and Zahman, J. (1992). Extending and formalizing the framework for ISs

architecture. IBM Systems Journal , 31(3), 590-616.

19. Tkach, D., Fang, W., and So, A. (1996). Visual Modeling Technique: Object Technology

Using Visual Programming. Addison-Wesley.

20. Trujillo, J., Soler, E., Fernández-Medina, E. and Piattini, M. (2009). A UML 2.0 profile to

define security requirements for Data Warehouses. Computer Standards & Interfaces 31 ,

969–983.