Model Checking Veriﬁcation of Web Services

Composition

Abdallah Missaoui

, Zohra Sba

and Kamel Barkaoui

Ecole Nationale d’Ing

enieurs de Tunis, BP. 37 Le Belv

ere, 1002 Tunis, Tunisia

Conservatoire National des Arts et M

etiers, Rue Saint Martin, 75141 Paris, France

Abstract. Web services composition is becoming very important in today’s ser-

vice oriented business environment. Different services frequently have semantic

inconsistencies which may lead to the failure of the services composition. In order

to verify the correctness of the Web Services composition, we present a method

for analyzing and verifying interactions among web services. We model web ser-

vice composition based on special class of Petri nets: open workﬂow nets. We

translate this composition to Promela, a source language of SPIN model checker,

designed to describe communicating distributed services. At the requirements

level, model checking is used to validate the speciﬁcation against a set of formu-

lae speciﬁed into LTL which are used to verify constraints satisfaction of web

services composition.

1 Introduction

Founded on standard protocols, Web service is a kind of software interface and plat-

form, which is described, published and invoked through the Internet. Web services

have the capability of implementing distributed applications. Recently, integrating var-

ious services distributed becomes a valuable issue in current research on Web services.

The behaviour of a service composite may become very complex due to the com-

plex of the communication between partners. The tasks that are performed within a

service generally depend strongly on the interaction that has taken place. Thus, it is

very important to decide whether all services interact properly. At present, many indus-

try and academia researchers are paying attention to ﬁnd some methods to detect these

behaviour problems such deadlock.

Model checking is a veriﬁcation technique that explores all possible system states

in a brute-force manner. A model checker, the software tool that performs the model

checking, examines all possible system scenarios in a systematic manner. In this way,

it can be shown that a given system model truly satisﬁes a certain property. There are

many powerful model checkers such as NuSMV [4], BLAST [5] and SPIN [6, 7].

This paper proposes to use the software model checking techniques for the veriﬁca-

tion of web services composition. We adapt Petri nets to describe services interaction

and use SPIN model checker as a veriﬁcation engine. First, a composed system model

is written in Promela (PROcess MEta LAnguage) that describes the behaviour of the

web services composition. Then, correctness properties that express requirements on

Missaoui A., Sbaï Z. and Barkaoui K. (2010).

Model Checking Veriﬁcation of Web Services Composition.

In Proceedings of the 4th International Workshop on Architectures, Concepts and Technologies for Service Oriented Computing, pages 114-126

DOI: 10.5220/0003051501140126

 SciTePress

the system’s behaviour are speciﬁed in Linear Temporal Logic (LTL). By efﬁcient ex-

ploration of the complete set of states generated from the Promela speciﬁcation, SPIN

verify LTL formulae corresponding to properties of web service composition.

The rest of this paper is organized as follows. Section 2 presents preliminaries.

Section 3 focuses on Petri net model of web service composition as well as our Promela

implementation of this composition. In section 4, We formulate in LTL some soundness

properties to be veriﬁed by SPIN. In section 5, we study an example of web service

composition. We discuss in section 6 some related work. Section 7 concludes the paper.

2 Preliminaries

2.1 Workﬂow Process Modelling

Petri nets are a well founded process modeling technique that have formal semantics.

They are one of the best known techniques for specifying business processes in a formal

and abstract way. The semantics of process instances ensuing from process models

described in Petri nets are well deﬁned and not ambiguous.

We choose to adopt open workﬂow nets [17] for web service modelling. Open work-

ﬂow nets result from the application of Petri nets to workﬂow management. In fact,

Petri nets have been used for their formal semantics, graphical nature, expressiveness,

analysis techniques and tools.

In the rest of this section, we present ﬁrst the basic deﬁnitions and notations of Petri

nets [2] used in this work. Then we highlight the notion of open workﬂow nets.

Petri Nets

A Petri net is a 4-tuple N = (P, T, F, W ) where P and T are two ﬁnite non-empty sets

of places and transitions respectively, P ∩ T = ∅ , F ⊆ (P × T ) ∪ (T × P ) is the

ﬂow relation, and W : (P × T ) ∪ (T × P ) → N is the weight function of N satisfying

W (x, y) = 0 ⇔ (x, y) /∈ F .

If W (u) = 1 ∀u ∈ F then N is said to be ordinary net and it is denoted by N =

(P, T, F ).

For all x ∈ P ∪ T , the preset of x is

•

x = {y |(y, x) ∈ F } and the postset of x is

•

= {y|(x, y) ∈ F }.

A marking of a Petri net N is a function M : P → N. The initial marking of N is

denoted by M

A transition t ∈ T is enabled in a marking M (denoted by M[ti) if and only if ∀p ∈

•

t : M (p) ≥ W (p, t). If transition t is enabled in marking M, it can be ﬁred, leading to

a new marking M

such that: ∀p ∈ P : M

(p) = M (p) − W (p, t) + W (t, p).

The ﬁring is denoted by M[tiM

. The set of all markings reachable from a marking M

is denoted by [Mi.

For a place p of P, we denote by M

the marking given by M

(p) = 1 and M

) = 0

∀p

6= p.

Petri nets are represented as follows: places are represented by circles, transitions by

boxes, the ﬂow relation is represented by drawing an arc between x and y whenever

(x, y) is in the relation, and the weight function labels the arcs whenever their weights

are greater than 1. A marking M of a Petri net is represented by drawing M(p) black

tokens into the circle representing the place p.

Open Workﬂow Nets (oWF-nets)

In this paper, we choose to adopt a special class of Petri-nets which is open workﬂow-

nets (oWF-net), for web service modeling. It generalized the classical workﬂow nets

[1] by introducing an interface for asynchronous messages with partners. A petri net

N = (P, T, F ) is called an oWF-net, if:

i. P is composed from disjoint sets: internal places P

, input places P

and output

places P

;

ii. For all transition t ∈ T : p ∈ P

(resp. p ∈ P

) implies (t, p) 6∈ F (resp. (p, t) 6∈

F );

iii. F does not contain cycles.

In all examples in this paper, an oWF-net are initially one token in start place (no

tokens in other places including the interface places).

Open workﬂow nets allow diverse analysis methods of business process. Moreover,

the explicit modeling of interface allows the veriﬁcation and behaviour analysis of web

service composition.

2.2 Model Checking Techniques

Model checking is a veriﬁcation technique that explores all possible system states in a

brute-force manner. Similar to a computer chess program that checks possible moves,

a model checker, the software tool that performs the model checking, examines all

possible system scenarios in a systematic manner. In this way, it can be shown that a

given system model truly satisﬁes a certain property. It is a real challenge to examine

the largest possible state spaces that can be treated with current means, i.e., processors

and memories.

There are many powerful model checkers such as NuSMV, BLAST and SPIN.

The SPIN model checker is a system that can verify models of computerized sys-

tems. The name SPIN was originally chosen as an acronym for Simple Promela INter-

preter. It can be used in two basic modes: as a simulator and as a veriﬁer. In simulation

mode, SPIN can be used to get a quick impression of the types of behavior that are cap-

tured by a system model, as it is being built. Some optimization techniques, e.g., partial

order reduction and graph encoding, are available to help reduce the usage of CPU time

or memory space.

2.3 Linear Temporal Logic

SPIN checks properties formulated with Liner Temporal Logic. An LTL formula f

may contain any lowercase propositional symbol p, combined with unary or binary,

Boolean and/or temporal operators. Propositional and temporal operators are presented

in ﬁgure 1.

The semantics of a formula is given in terms of computations and the states of a

computation. The atomic propositions of temporal logic can be evaluated in a single

state independently of a computation.

Propositional Operators

&& conjunction k disjunction

− > implication ! Negation

Temporal Operators

[] always  eventually

until

Fig. 1. Propositional and Temporal Operators.

3 Web Services Composition

In this section, we begin with a speciﬁcation of services in terms of open Workﬂow net

and Promela language. Then, we model the composition of web services and we give a

veriﬁcation method by means of model checking techniques.

The formalism of open Workﬂow net is meant to model complex, distributed com-

puting systems with well deﬁned semantics. Web services composition can be checked

against requirements such as the mentioned above. The properties that are to be checked

need to be formulated based on temporal logic, relate to the Promela speciﬁcation of

workﬂow representation of web service composition. SPIN Model checker will evaluate

these LTL formulae.

3.1 Modeling Web Service Composition

Using oWF-nets, we can model business process. We can furthermore compose two or

many oWF-nets and describe the web services interaction with partners.

The communication between two oWF-nets is based on interface places (unidirec-

tional). Given two oWF-nets N1 and N2, their composition is the result of merging one

or many input places of one oWF-net with suitable output net of the other place and

vice versa. Each oWF-net shares only interface places with other oWF-nets.

Fig 2.a shows the composition of two oWF-nets: Producer and Consumer. Each

of which has one input place and one output place. Shared places which model the

interfaces are represented by dashed lines. The consumer of the left side sends an order

message to the producer in order to execute its task. In the right side, the producer

executes the task and then sends a response to consumer.

3.2 Promela Implementation

Like structured programming languages, in Promela we can use variables and subrou-

tines such as proctype. The proctype construct is used for the declaration. It can be

used to declare process behavior is to be executed completely deterministically. Each

process behavior must be declared before process instantiation. This instantiation can

be done either with the run operator, or with the preﬁx active that can be used at

the time of declaration. The types of variables are sets of integer in order to guarantee

that the program has ﬁnite state space. This section presents a method to use the SPIN

model checker for the representation of the web services composition and analysis. The

basic idea is just to translate a composition of oWF-nets into Promela source program.

web services models communicate through interface places modeled by variables. We

adopt an approach of oWF-net introduced by [17] to model web services composition.

Workﬂow module deﬁnes its internal behaviour without interface places that are used

to represent message ﬂow between partners.

Based on the deﬁnition of workﬂow module, we present a web service speciﬁcation

in Promela language. This speciﬁcation is described in terms of the marking of places

and the ﬁring count of transitions. Hence, we use the following conventions:

– Places are represented by an array P L of integers with length equal to the number

of places. This array contains initially zero in each element.

– Transitions are modelled by an array TR of integers (initialized to zero) with length

equal to the number of transitions.

The behaviour of a web service can be described in terms of system states and their

changes. A marking is initialized to M

and it is changed according to the following

transition rule: A transition t is enabled if each input place p of t is marked. Moreover,

an enabled transition t may or may not ﬁre, and a ﬁring of t removes one token from

all p ∈

•

t and adds one token to each output place of t. These concepts are translated

in the corresponding Promela description of a workﬂow module as follows: The ﬁring

of a transition consists on decreasing by 1 the integer corresponding to each place p ∈

•

t in the array P L and increasing by 1 the elements of P L corresponding to the output

places (p ∈ t

•

). Although, we increase by 1 the element of T R corresponding to the

transition t to mark that t is ﬁred once.

These modiﬁcations are made by the macro add1, add2, ..,addS, remove1, remove2,

.., and removeK where S is the maximum number of possible input places and K is

the maximum number of possible output places.

To ﬁre a transition t which has I input places and J output places, we call these

macros with the appropriate arguments in order to achieve the following actions:

1. removeI(p

, p

, .., p

) destructs one token from each input place. It tests if these

input places are marked (PL[index of p

] > 0, 1 ≤ j ≤ I) and if this condition is

satisﬁed, it removes one token from each of its parameters.

2. We increase the element corresponding to t in T R.

3. And ﬁnally addJ(p

, p

, .., p

) creates one token in each output place.

Complex inter-organizational business processes are structured as a set of commu-

nicating elementary services. A service represents a self contained software unit that

offers an encapsulated functionality over a well deﬁned interface.

Several languages, such as BPEL [3], are used to describe the composition of services.

The behaviour of a service composite may become very complex due to the nature of

the communication between partners. The tasks that are performed within a service

generally depend strongly on the interaction that has taken place. Thus, analyzing the

behaviour of a service on the one hand and the veriﬁcation of its interaction with part-

ners on the other hand are very important to perform and improve inter-organizational

business processes.

Web services composition is modeled based on oWF-nets. Interface places are repre-

sented, in our speciﬁcation, by an array I of integers with length equal to the number

of places in web services composite. Each element of this array, that initialized to zero,

perform the communication between services partners, and for each place, when one

service increment element of I (add token in interface place), another partner consume

a token and decrement this element by 1. Figure 2.a shows an example of web service

# d e f i n e PLACEC 3

# d e f i n e TRANSITIONC 2

# d e f i n e PLACEP 3

# d e f i n e TRANSITIONP 2

# d e f i n e INTERFACE 2

# d e f i n e re mo ve 1 ( x1 ) ( x1>0)−>x1−−

# d e f i n e re mo ve 2 ( x1 , x2 )

( x1>0 && x2>0)−>x1−−; x2−−

# d e f i n e a dd 1 ( x 1 ) x1 ++

# d e f i n e a dd 2 ( x1 , x2 ) x1 ++ ; x2++

i n t M2[ PLACEC ] ; i n t X2 [ TRANSITIONC ] ;

i n t M1[ PLACEP ] ; i n t X1[ TRANSITIONP ] ;

i n t I [INTERFACE]

p ro c t y p e Con sum er ( )

{M2 [ 0 ] = 1 ;

: : a tom i c{r em ov e1 (M2[0])−>X2[ 0 ] + + ;

ad d2 (M2[ 1 ] , I [ 0 ] ) }

: : a tom i c{r em ov e2 (M2 [ 1 ] , I [1])−> X2 [ 1 ] + + ;

ad d1 (M2[ 2 ] ) }

}

p ro c t y p e P r o d u c e r ( )

{M1 [ 0 ] = 1 ;

: : a tom i c{r em ov e2 (M1 [ 0 ] , I [0])−>X1 [ 0 ] + + ;

ad d1 (M1[ 1 ] ) }

: : a tom i c{r em ov e1 (M1[1])−>X1[ 1 ] + + ;

ad d2 (M1[ 2 ] , I [ 1 ] ) }

}

i n i t

{

at o mi c{

run Co nsum er ( ) ;

run P r o d u c e r ( ) ;

}

(a) (b)

Fig. 2. The process with two services.

composition based on two oWF-nets. The consumer communicates with producer by

means of two interface places. The ﬁgure 2.b represents the Promela description of this

composed system.

4 Veriﬁcation

SPIN allows Promela systems to be simulated, either step-by-step or randomly. Addi-

tionally, it is possible to execute an exhaustive simulation by generating the complete

state-space of the system. This allows us to verify if the system requirements are satis-

ﬁed.

In web service architecture, by composing various services, complex activities (e.

g., inter-organizational business processes) can be realized. Hence, the correct interplay

of distributed services is crucial to accomplish a common goal. The ﬂow should have

safety properties such as deadlock freedom. At the same time, the ﬂow should satisfy

some properties since it is executed in an environment.

In this section, we discuss how to verify a given composed oWF-net speciﬁcation

using the SPIN model checher. The input language of SPIN is Promela, which is a lan-

guage for modeling web services composition. SPIN verify LTL properties of Promela

speciﬁcation. We implement the veriﬁcation process in three steps : (1)we model the

composed web services based on oWF-net; (2)we translate this composed system to

Promela processes with communication based on an interface array; (3)we deﬁne prop-

erties in LTL and we check if the system satisﬁes or not these properties.

The requierement needs to be formulated as LTL formulas. All logical variables

used in the formula must be deﬁned by def ine macro. Using logical variables inte-

grated in TLT formulae, all properties are veriﬁed on the ﬂy. It is not necessary to

generate the whole state space to detect errors. However, to verify that properties are

satisﬁed, the whole state space may be generated.

4.1 Termination

Several Technologies [9–11] have been proposed in order to automatically compose

Web services to perform some desired task. Regardless of how the compositions orig-

inated, we are interested here in describing and verifying properties of these services

by simulating their executions under different input conditions. Deadlock is a condition

which states that the composed system is deadlocked, i.e. it is neither terminated nor

more activities could be executed.

The language source used by SPIN (Promela) describe the behaviour of a web ser-

vices composition based on interactions between the service and its partners. SPIN can

simulate and validate a model in Promela language and it can accept constraints de-

scribed in LTL formulae.

Never−c l a i m :

n e v e r { /∗ !(<>p ) ∗/

a c c e p t

i n i t :

T 0 i n i t :

i f

: : ( ! ( ( p ) ) ) −> g o t o T 0 i n i t

f i ;

}

Fig. 3. Never-claim corresponding to F .

The formula F : ♦p ( p is declared in Promela source as (M1[index of f 1] ≥ 1

&& M2[index of f 2] ≥ 1)) allows us to check if the process, given in ﬁgure 2,

completes successfully. First, SPIN translates a negative form of formula into a never-

claim statement. Second, SPIN validates the model S with this statement. The never-

claim (generated by SPIN) corresponding to formula F is given in ﬁgure 3.

Never claim is the Promela model of the B

uchi automaton(ﬁgure 4) corresponding

to the LTL formula F . It is used to represent a property that should never be satisﬁed

during the execution of a model. Then, if S contains an acceptance cycle then a counter-

example to F exists and this proves that the model does not satisfy the property.

4.2 Soundness

Composing web services and guarantying the correctness of the design is an important

and challenging problem in web services.

An oWF-net is a more suitable model for analysis and veriﬁcation of web services

composition. Several Correctness criteria, like liveness and termination, should be valid

for single process and for the combined model. In this section, we give a method to

verify some properties of web services composition. For each of them, we deﬁne the

property of the composed oWF-nets. We also give an LTL formula that allows to verify

it based on corresponding Promela speciﬁcation of web services composition.

A workﬂow process is sound if, for any case, termination is guaranteed, there are

no dangling references, and deadlocks and livelocks are absent. This dynamic property

is decidable and it can be checked in polynomial time. Soundness property is proved

in [18] equivalent to liveness and boundedness, thus it can be veriﬁed by standard Petri

net methods.

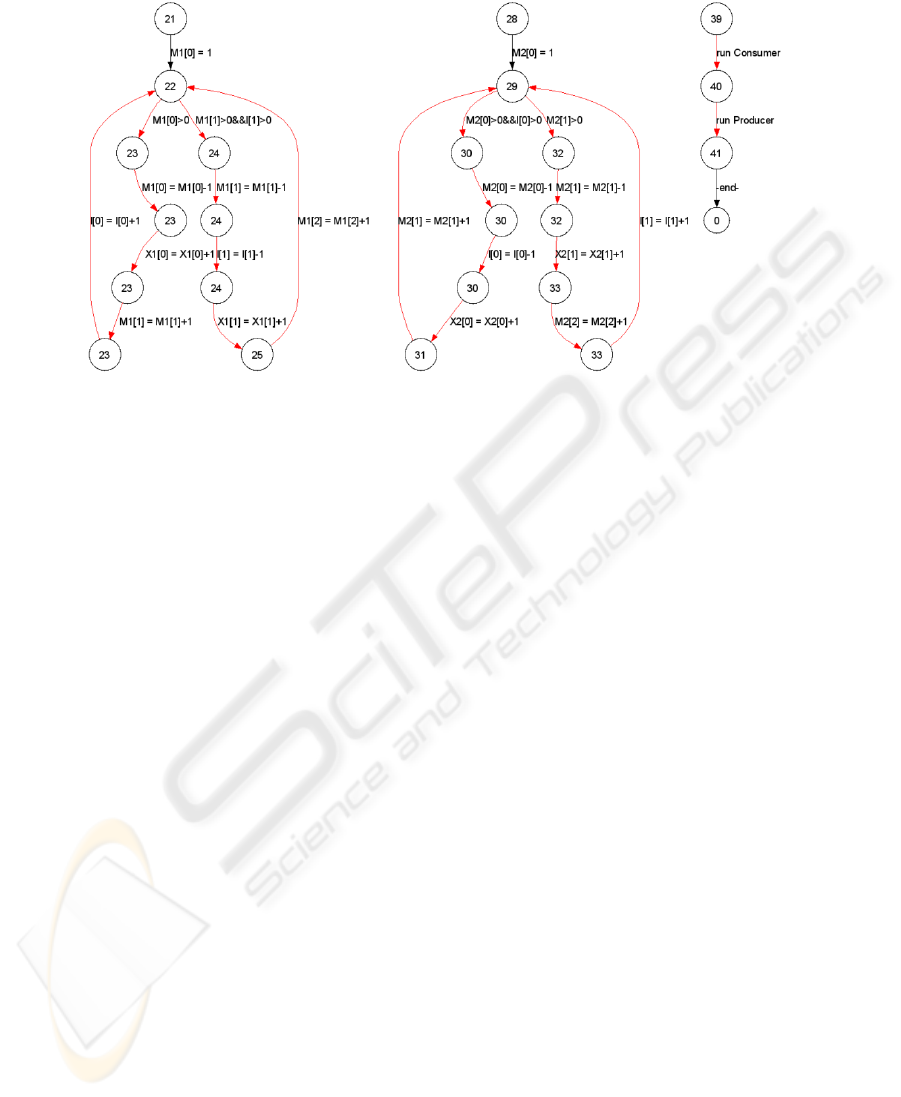
Fig. 4. A b

uchi automata.

The extension of this soundness deﬁnition in the context of web service composi-

tion via oWF-nets is given in the following deﬁnition 1. The overall net describing the

composition can be seen as a classical petri net with a speciﬁc initial marking and its

soundness is given in terms of states evolution and transitions ﬁring. Thus the veriﬁca-

tion of this property is decidable.

Deﬁnition 1. (Soundness)

Let N

= (P

, T

, F

), N

= (P

, T

, F

),..., and N

= (P

, T

, F

) be x oWF-net.

The composed oWF-nets W C = (P, T, F ) from N1, N2 and Nx, is called sound if

and only if the following three requirements are satisﬁed:

i Termination: For each reachable marking (reachable from M

= [i

, i

, .., i

], )

the ﬁnal marking M

= [f

, f

, .., f

] is reachable;

ii Proper completion: For each reachable marking, if M ≥ M

holds then M = M

;

iii No dead transition: It makes certain that starting from the initial state (just one

token in every initial place), it is always possible to reach the state with one token

in every ﬁnal place.

We can deﬁne LTL formulae based soundness of web service composition by study-

ing the three sub-properties: Completion, Proper Completion and Deadlock-freedom:

i ♦(

i=x

i=1

M[index of f

] ≥ 1)

ii (

i=x

i=1

M[index of f

] ≥ 1) ⇒ (M = [f

, f

, .., f

])

iii ¬(( k

t∈T

X[index of t] == 0))

To verify soundness of web service composition, we have to check the three preceding

formulae.

Weak soundness properties are introduced by Martens [8] in the context of web

service composition. We can allow service that exhibits a proper behaviour but not

all tasks. The overall Composed system is weak sound, because the ﬁnal state can be

reached from each state reachable from the initial state, and when the ﬁnal state M

reached, no other token remains in the net.

Using Petri nets notation, we give the following deﬁnition of weak soundness.

Deﬁnition 2. (weak soundness)

a composed system N = (P, T, F ) is called weak sound if and only if:

i. For each reachable marking (reachable from M

) the ﬁnal marking f is reachable.

ii. For each reachable marking, if M ≥ M

holds then M = M

Based on LTL formulae, corresponding to Termination and Proper Completion, de-

ﬁned in this section, we can verify weak soundness properties of the web service com-

position.

5 Case Study

Figure 5 presents an example of web service composition. The overall ﬂow of this ex-

ample is as follows: A traveler will plan her trip. When the traveler is ﬁnished with

specifying the details of the trip plan, she sends this information together with the pre-

pared details (example of details concern the list of participants) to the travel agent.

Next, the traveler will await the submission of the electronic tickets as well as the ﬁnal

itinerary for the trip. When the agent receives the traveler’s trip order, he will determine

the legs for each of the stages, which includes an initial seat reservation for each of the

participants as well as the rate chosen. To actually make the corresponding ticket orders

the agent submits these legs together with the information about the credit card to be

charged to the airline company.

Then, the agent will wait for the conﬁrmation of the ﬂights, which especially in-

cludes the actual seats reserved for each of the participants. This information is com-

pleted into an itinerary, which is then sent to the traveler.

When the airline receives the ticket order submitted by the agent, the requested

seats will be checked. After that, the credit card will be charged, and the updated leg

information is sent back to the agent as conﬁrmation of the ﬂights. After that, the airline

sends the electronic tickets (by e-mail) to the traveler. Information about the recipient

of the tickets is passed to the agent as well as to the airline.

In this example, we propose to draw its Promela model as follows: we begin with

specifying each process as a single process deﬁned by proctype construct. The pro-

cesses describing the work of the traveler, the agent and the airline are given respec-

tively in the following source code.

Fig. 5. Travel Plan Example.

p ro c t y p e T r a v e le r ( )

{PL1 [ 0 ] = 1 ;

: : a t om i c{i n p 1 ( PL1 [ 0 ] ) −> TR1 [ 0 ] + + ; o u t 1 ( PL1 [ 1 ] ) }

: : a t om i c{i n p 1 ( PL1 [ 1 ] ) −> TR1 [ 1 ] + + ; o u t 3 ( PL1 [ 2 ] , PL1 [ 3 ] , I [ 0 ] ) }

: : a t om i c{i n p 2 ( PL1 [ 2 ] , I [ 4 ] ) −> TR1 [ 2 ] + + ; o u t 1 ( PL1 [ 4 ] ) }

: : a t om i c{i n p 2 ( PL1 [ 3 ] , I [ 1 ] ) −> TR1 [ 3 ] + + ; o u t 1 ( PL1 [ 5 ] ) }

: : a t om i c{i n p 2 ( PL1 [ 4 ] , PL1 [ 5 ] ) −> TR1 [ 4 ] + + ; o u t 1 ( PL1 [ 6 ] ) }

od }

p ro c t y p e A ge nt ( )

{PL2 [ 0 ] = 1 ;

: : a tom i c{i n p 2 ( PL2 [ 0 ] , I [ 0 ] ) −> TR2 [ 0 ] + + ; o u t 1 ( PL2 [ 1 ] ) }

: : a tom i c{i n p 1 ( PL2 [ 1 ] ) −> TR2 [ 1 ] + + ; o u t 1 ( PL2 [ 2 ] ) }

: : a tom i c{i n p 1 ( PL2 [ 2 ] ) −> TR2 [ 2 ] + + ; o u t 2 ( PL2 [ 3 ] , I [ 2 ] ) }

: : a tom i c{i n p 2 ( PL2 [ 3 ] , I [ 3 ] ) −> TR2 [ 3 ] + + ; o u t 1 ( PL2 [ 4 ] ) }

: : a tom i c{i n p 1 ( PL2 [ 4 ] ) −> TR2 [ 4 ] + + ; o u t 1 ( PL2 [ 5 ] ) }

: : a tom i c{i n p 1 ( PL2 [ 5 ] ) −> TR2 [ 5 ] + + ; o u t 2 ( PL2 [ 6 ] , I [ 1 ] ) }

od }

p ro c t y p e A i r l i n e ( )

{PL3 [ 0 ] = 1 ;

: : a tom i c{i n p 2 ( PL3 [ 0 ] , I [ 2 ] ) −> TR3 [ 0 ] + + ; o u t 1 ( PL3 [ 1 ] ) }

: : a tom i c{i n p 1 ( PL3 [ 1 ] ) −> TR3 [ 1 ] + + ; o u t 1 ( PL3 [ 2 ] ) }

: : a tom i c{i n p 1 ( PL3 [ 2 ] ) −> TR3 [ 2 ] + + ; o u t 1 ( PL3 [ 3 ] ) }

: : a tom i c{i n p 1 ( PL3 [ 3 ] ) −> TR3 [ 3 ] + + ; o u t 2 ( PL3 [ 4 ] , I [ 3 ] ) }

: : a tom i c{i n p 1 ( PL3 [ 4 ] ) −> TR3 [ 4 ] + + ; o u t 2 ( PL3 [ 5 ] , I [ 4 ] ) }

od }

Note that in each process, the ﬁring of a transition leads to add tokens not only in

its own places but also in interface ones. The interface places are modelled by an ar-

ray called I of ni elements with ni is the number of these places. The initial process,

declared by init, initializes global variables, and instantiates processes via the run

statement. This statement is used as a unary operator that takes the name of a process

type. An executing process disappears again when it terminates (i.e., reaches the end

of the body of its process type declaration), but not before all processes that it started

have terminated. The sequence of composed processes has to be executed as one indi-

visible unit, non-interleaved with any other processes. Hence, we preﬁx the sequence

of processes instantiations by atomic.

i n i t

{

at o mi c {

run T r a v e l e r ( ) ;

run A gent ( ) ;

run A i r l i n e ( )

}

To verify soundness of web services composition, three requirements need to be for-

mulated as LTL formula. We introduce logical variables that take part from the LTL

formula in the source code. Using the Promela source and the logical variable deﬁni-

tions, SPIN evaluates the LTL formula. The web service composition presented in ﬁg

5 is sound because it satisﬁes the three formulae (termination, proper completion and

deadlock-freedom).

For example, the evaluation of a formula F (<> p) of termination (p: P L1[6] >

0 && P L2[6] > 0 && P L3[5] > 0 ) have resulted in positive answers given that the

number of errors returned by SPIN is 0. This positive result guarantees that the Promela

model meets this requirement. All states have been explored by SPIN and the result

generated shows that the number of states explored is 24.

6 Related Works

Many works such as [8, 16, 15] introduce formal method based on Petri nets for describ-

ing and verifying web service composition. In [15], semantics of Petri nets is deﬁned by

mapping BPEL process to a Petri net. A formal model of BPEL can be generated and

allows the veriﬁcation techniques developed for Petri nets to be exploited in the context

of BPEL processes. Lohmann [16] focuses on the problem of analyzing the interaction

between WS-BPEL processes. A BPEL process is seen as an open workﬂow net by an

interface specifying the interactional behaviour of this process with its partners. The

framework developed in this context allows the generation of compact Petri net models

and gives a formal analysis of processes behaviour and a veriﬁcation of controllability.

Some research efforts have already been proposed to use model-checking tech-

niques for web service veriﬁcation. Nakajima [12] describes a method based on model

checking to verify web service ﬂow description. The language adopted to describe web

service composition is Web Services Flow Language (WSFL). The model checker used

in their veriﬁcation engine is SPIN. This paper presents means to translate WSFL prim-

itives into PROMELA. In [13], Nakajima proposed to extract behaviour speciﬁcation

from BPEL processes to a variant of Extended Finite-state Automaton. Then, Automa-

ton model is translated to PROMELA and is analyzed by SPIN model checker. Never-

theless, not all BPEL processes can be analyzed i.e. it does not deal with the semantics

of handlers such as exception or compensation.

Bao [14] provides a model checking method to Verify BPEL4People processes that

can detect deadlocks and validate constraints based on LTL. A tool is developed to

translate BPEL4People process to promela automatically but it didn’t support all feature

activities.

7 Conclusions

In this paper, we have presented a speciﬁcation and veriﬁcation method of web services

composition based on model checking. The interactions among the partners participat-

ing to a web services composition are modeled by Open WorkFlow nets (OWF-nets),

where the communication is ensured by interface places. Hence, we begun with convert-

ing OWF-nets to Promela: the model speciﬁcation language used to deﬁne the relevant

aspects of the system needed to verify it.

The formal model presented in this paper captures and checks the control ﬂow and

the dynamic behaviour based on Promela speciﬁcation that describes the behaviour

of the web services composition. After this step, we have speciﬁed in Linear Temporal

Logic (LTL) correctness properties that express requirements on the system’s behaviour.

Especially, we have deﬁned the soundness properties of the web service composition in

terms of LTL formulae.

Once the formal model and the correctness properties are deﬁned, SPIN model

checker veriﬁes LTL formulae corresponding to properties of web service composition,

by efﬁcient exploration of the set of states generated from the Promela speciﬁcation.

We propose to extend this work by deﬁning additional veriﬁcation criteria which

are suitable for the composition of web services such as controllability.

References

1. van der Aalst, W.M.P.: The Application of Petri Nets to Workﬂow Management. The Journal

of Circuits, Systems and Computers, vol. 8, (1998) 21-66

2. Barkaoui, K., Ben Ayed, R., Sba

ı, Z.: Workﬂow Soundness Veriﬁcation based on Structure

Theory of Petri Nets. International Journal of Computing and Information Sciences (IJCIS),

Vol. 5(1), (2007) 51–61

3. Lohmann, N., Massuthe, P., Stahl, C., Weinberg, D.: Analyzing interacting WSBPEL pro-

cesses using ﬂexible model generation. DKE 64(1), (2008) 3854

4. Cimatti, A., Clarke, E. M., Giunchiglia, E., Giunchiglia, F., Pistore, M., Roveri, M., Sebas-

tiani, R. and Tacchella, A.: NuSMV 2: An OpenSource Tool for Symbolic Model Checking.

In Proceeding of International Conference on Computer-Aided Veriﬁcation, (2002)

5. Henzinger, T. A., Jhala, R., Majumdar, R. and Sutre, G.: Software Veriﬁcation with Blast.

In Proceedings of the 10th SPIN Workshop on Model Checking Software (SPIN), Lecture

Notes in Computer Science 2648, Springer-Verlag, (2003) 235-239

6. Holzmann, G. J.: The SPIN Model Checker, Primer and Reference Manual. Addison-Wesley,

(2003)

7. Holzmann, G. J.: The Model Checker SPIN. IEEE Transactions on software engineering,

vol.23, no.5, (1997)

8. Martens, A.: Analyzing web service based business processes. In Proceeding of International

Conference on Fundamental Approaches to Software Engineering, Part of the European Joint

Conferences on Theory and Practice of Software, Lecture Notes in Computer Science vol.

3442, Springer-Verlag, (2005)

9. Leymann, F.: Web Services Flow Language (WSFL 1.0). IBM Corporation, May 2001.

10. Business Process Execution Language for Web Services (BPEL), Version 1.1, http://www-

128.ibm.com/developerworks/library/ speciﬁcation/ws-bpel. (2002)

11. Thatte, S.: XLANG: Web Services For Business Process Design, Microsoft Corporation,

(2001), (http://www.gotdotnet.com/team/xml wsspecs/xlang-c/default.htm)

12. Nakajima, S.: Veriﬁcation of Web service ﬂows with model-checking techniques, presented

at First International Symposium on Cyber Worlds, (2002)

13. Nakajima, S.: Model-Checking Behavioral Speciﬁcation of BPEL Applications. Electronic

Notes in Theoretical Computer Science 151 (2006) 89105

14. Bao, F., Zhang, L.: A Model Checking Method to Verify BPEL4People Processes. on The

IEEE Symposium Advanced Management of Information for Globalized Enterprises. (2008)

15. Hinz, S., Schmidt, K., Stahl, C.: Transforming BPEL to Petri nets. Business Process Man-

agement, LNCS, vol. 3649, (2005) 220235.

16. Lohmann, N., Massuthe, P., Stahl, C. and Weinberg, D.: Analyzing interacting WS-BPEL

processes using ﬂexible model generation, Data and Knowledge Engineering 64 (2008) 3854

17. Massuthe, P., Reisig, W., Schmidt, K.: An operating guideline approach to the SOA, Annals

of Mathematics, Computing and Teleinformatics 1 (3) (2005) 3543

18. van der Aalst, V.M.P.: Structural characterization of sound workﬂow nets, Computing Sci-

ence Report 96/23, Eindhoven University of Technology, (1996)