AUTOMATIC ONTOLOGY CONSTRUCTION

FOR MANUFACTURING KNOWLEDGE

AND INFORMATION MANAGEMENT

X. Hou, W. J. Liu

School of Mechatronics Engineering, Harbin Institute of Technology, 150001, Harbin, China

S. K. Ong, A. Y. C. Nee

National University of Singapore, 9 Engineering Drive 1, 117576, Singapore, Singapore

Keywords: Knowledge management, Information management, Ontology.

Abstract: Domain ontology is a natural approach for representing manufacturing domain knowledge. A large amount

of manufacturing domain knowledge, entities and their properties is embodied in documents. Automatic

construction of ontology from these documents is therefore essential for knowledge and information

management. A graph-based approach to automate ontology construction for fixture design is presented.

Each document in a collection is represented by a graph. The information contained in a term is estimated

from both local and global perspectives. Methods are proposed to disambiguate terms with different

meanings and group similar terms to produce concepts, and find arbitrary latent relations among them.

1 INTRODUCTION

Domain ontology provides a common and

unambiguous understanding of the domain for both

the users and the system to communicate and share

knowledge and information with each other in an

enterprise (Studer, Benjamins and Fensel, 1998;

Kjellberg et al., 2009). Most knowledge concerning

domain entities, e.g., properties and relationships, is

embodied in document collections. Extracting

ontology from these documents is an important

means of ontology construction. Manual ontology

construction is the current dominant means to

acquire domain knowledge. However, it is a difficult

and time-consuming task that involves domain

modellers and knowledge engineers (Navigli,

Velardi and Gangemi, 2003). Present techniques for

domain ontology construction from unstructured or

structured natural language documents have a few

drawbacks (Weng et al., 2006). Concepts extraction

still mainly depends on heuristic rules provided by

the domain corpus and dictionary although the

information may not be explicitly available for some

domains. Hierarchical and taxonomic relationships

are the main objects extracted from the concepts,

although other types of relationships, e.g.,

chronological, are also essential for modelling a

domain. It is difficult to ensure that the ontology

obtained is correct, complete and meets the needs of

an application as the document collection used for

ontology construction may not encompass a domain.

This paper presents a graph-based automatic

ontology construction approach for knowledge and

information management. To the best of the authors’

knowledge, this is the first work that addresses

ontology construction using graph-based methods.

2 GRAPH-BASED ONTOLOGY

CONSTRUCTION ALGORITHM

Figure 1 shows the proposed graph-based approach

for automatic construction of domain ontology.

Document pre-processing converts domain

documents into the correct format that can be used in

the subsequent steps in ontology construction. It

removes stop words that are irrelevant to the text

meanings, reduces inflected words to their stems,

tags part of a speech for each remaining term

(Toutanova and Manning, 2000), and counts the

331

Hou X., Liu W., Ong S. and Nee A..

AUTOMATIC ONTOLOGY CONSTRUCTION FOR MANUFACTURING KNOWLEDGE AND INFORMATION MANAGEMENT.

DOI: 10.5220/0003053903310334

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 331-334

ISBN: 978-989-8425-29-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

frequency and adjacency information of the terms

and the term units, which are the basis for further

operation. This step results in the extraction of terms

with their frequency information and adjacency

information. They reflect how important a term or

term unit is to the documents to some degrees.

Structural information is captured by the structures

of the document graphs created based on the

adjacency information obtained.

The normalized frequency representation (Chow,

Zhang and Rahman, 2009) is adapted and used to

generate a graph for each document. An undirected

weighted graph with the vertices and edges

describing meaningful terms and connections

between the terms is used. Each vertex is labelled

with the term it represents, and only one vertex is

created regardless of the number of times it appears

in a document. The edge connecting two terms

indicates that they are adjacent in a document, and it

is labelled with the labels of both vertices connected

by it. Every vertex and edge is labelled with a

frequency measure that represents the total number

of occurrences (vertices) and co-occurrences

(edges). The frequency of a vertex or edge in a

large-size document will be larger than the same one

in a small-size document, even if the importance of

this term or relation is almost identical for both

documents. Therefore, the frequency is normalized

to reflect the actual importance of a term or relation

to the document size, by dividing each vertex

frequency either by the maximum vertex frequency

that occurs in the graph or the total frequencies of all

the vertices in the graph; a similar procedure is

performed for the edges.

Concept extraction consists of two steps, namely,

weighting terms based on random walks to measure

how informative a term is to the domain corpus and

using the Markov Clustering (MCL) algorithm

(Dongen, 2000) to cluster the weighted terms so as

to extract the candidate concepts.

In the random walk weighting process, the score

of each vertex is updated in each iteration with

regards to the new weights that its adjacent vertices

have accumulated, until all the vertices converge at a

pre-defined threshold. Since an undirected graph is

used, the score of each vertex (node) is calculated

using Equation (1) to estimate the importance of a

term to the domain corpus. After this step, the

weights of the nodes represent the estimates of how

informative the terms are to the domain corpus.

Neighbour( )

eighbour( )

() (1 ) ()

i j

VN V

WS V d d WS V



 



(1)

From Equation (1), it should be noted that the

edges incident to the vertices are used to derive the

similarity measures for the vertices using the

adjacency information. The vertex similarity is

estimated based on the structural properties of the

graph. Thus, it is domain independent and no further

knowledge is needed during this term weighting

step, making this ontology construction approach

suitable for other domains.

Figure 1: Graph-based ontology construction.

To cluster nodes, an edge should be weighted

with regards to the vertices it is connected. Equation

(2) assesses an edge based on the nodes that it is

connected, where

V and

V are two nodes connected

e . The edge weight is within the interval [0, 1].

() ()

()

() ()

WS V WS V

WE e

WS V WS V







(2)

Next, the MCL algorithm is used to cluster the

nodes of the graph with the new weights, and only

single-word terms are considered as candidate

concepts. However, there exist many multi-word

concepts in reality. Hence, after the candidate

concepts have been extracted, a post-processing step

is used to reconstruct the adjacent terms into multi-

word concepts. During post-processing, all candidate

concepts are marked on the nodes of the graph. If a

path exists that connects a sequence of adjacent

nodes, the candidate concepts represented by these

nodes are collapsed into a multi-word concept.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

332

Intuitively, a general and important relation in a

domain would appear frequently in the documents of

this domain, and this corresponds to a frequent sub-

structure of the graphs representing the documents.

Therefore, relation extraction for domain ontology

construction can be converted into discovering

frequent subgraphs within graphs describing the

domain-related corpus. Semantics should be

considered during the mining procedure since

relations discovered should have practical meanings,

rather than just combinations of terms. Thus, relation

extraction in this research is formulated as: given a

dataset of labelled-graph representations (each graph

representation corresponds to a document), a

taxonomy of concepts (concepts are outcomes of the

concept extraction step), a mapping from the labels

to the concepts, and a minimum support threshold,

find all the frequent informative subgraphs and

interpret them as relations.

The gSpan algorithm is used to discover the

frequent subgraphs (Yan and Han, 2002). An

information function defined in Equation (3) to

estimate the information contained in the subgraphs

is integrated into the gSpan algorithm to determine

the importance of the subgraphs.



is the frequency

that the subgraph g appears in the graph database.

The factor

()

g of the information related to the

subgraph g is the sum of the information carried by

the vertex

()vVg of weight

()

and the edge

()eEg of weight ()

we:

:( , ) ( )

ir r

sg Ig





(3)

() ()

() () ()

vV g eEg

givie







(4)

Information associated with a vertex or edge

weight are given in Equations (5) and (6)

respectively.

{| ,()()}

dDvdlv lv



   and

{| ,()()}

d D e dle le

  

  

are the subsets of graph

database D respectively.

()

() log

()





















(5)

()

() log

()

 



















(6)

Besides the information function, three

constraints are considered in relation extraction,

namely, (1) the concepts obtained from the prior step

are used to determine whether the current vertex

should be discovered as an element of one relation

when mining the frequent subgraphs; (2) for relation

extraction, the part-of-speech attribute of a term is

considered, i.e., each subgraph discovered must

contain at least one noun and one verb or adjective;

and (3) if the subgraphs mined contain vertices that

are not in the list of concepts, these vertices can be

added as concepts with respect to their term weights,

which can be regarded as the feedback from the

relations to the concepts.

After the frequent subgraph mining, the

subgraphs obtained will be interpreted as relations

between the concepts. A relation is described as a

triple {concept1, relation, concept2}. A general way

is to first locate the node labelled with a verb, and

find the adjacent nodes. If both adjacent nodes are

labelled with a noun, a relation between these three

terms is established. If one or both nodes are

labelled with a verb, these nodes are connected to

form a new node labelled with the union of the verb

labels. The new node will be used as the middle

word for the next iteration. This process is iterated

until two nodes labelled with a noun are connected

by a node labelled with a verb. Next, the two nouns

and the verb are interpreted as concept1 and

concept2 and the relation, respectively. This process

is applicable to a few nouns that are adjacent. A few

typical situations encountered in subgraph

interpretation are illustrated in Figure 2. It should be

noted that more than one relation may be extracted

from one subgraph; the number of relations

extracted from one subgraph depends on the number

of verb concepts in this subgraph as the core of a

relation is a verb term. Figure 3 shows an example

of frequent subgraph mining and the interpretation

of a subgraph as relations.

3 CONSTRUCTION OF FIXTURE

DESIGN ONTOLOGY

This section presents the construction of fixture

design ontology using the proposed approach. A

snippet of the ontology on “fixture design” is shown

in Figure 4. The new ontology created is compared

with a fixture design ontology FIXON to

demonstrate the validity of the proposed method.

Since the sources from which the two ontologies are

constructed are different, only the common parts of

the two ontologies are compared. From Table 1, the

performance of the proposed method as compared

with FIXON is as follows: the concept precision is

70.8%, the concept-location precision is 71.4%, and

the concept recall is 76.8%.

AUTOMATIC ONTOLOGY CONSTRUCTION FOR MANUFACTURING KNOWLEDGE AND INFORMATION

MANAGEMENT

333

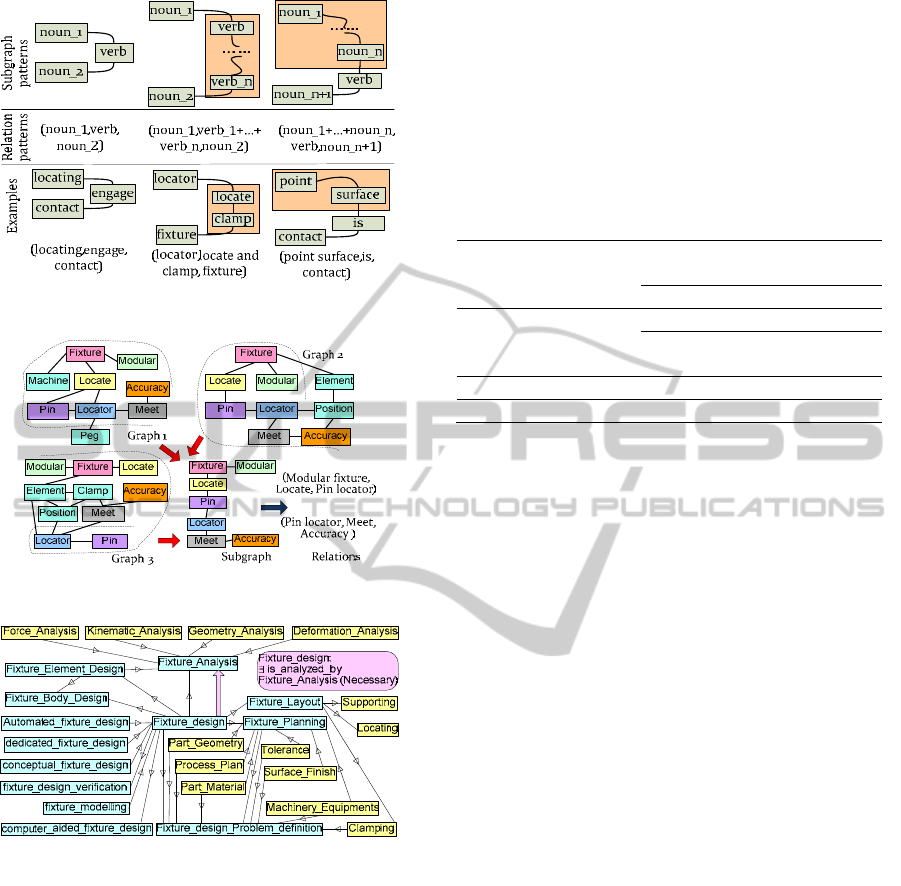
Figure 2: Mapping between subgraphs and relations.

Figure 3: Two relations extracted from a subgraph.



Figure 4: Fixture design ontology on “fixture design”.

4 CONCLUSIONS

A graph-based approach is proposed for automatic

construction of domain ontology for knowledge and

information management. The graph-based approach

simultaneously considers the frequency and

structural information of the domain corpus. The

major contributions are (1) a graph-based document

representation, where an ordered and structural

description that can preserve the inherent structure

of the original document can be obtained for concept

and relation extraction; (2) a concept extraction

method based on the random walk term weighting

scheme and graph clustering; (3) an arbitrary

relation extraction method based on frequent

informative subgraph mining instead of only

extracting predefined or hierarchical relations; and

(4) this proposed approach is unsupervised, flexible

and highly portable to different domains, genres, or

languages. In future work, abstract relations and

individual relations will be categorized to build up a

more complete relation hierarchy.

Table 1: Performance of proposed approach.

Concepts/relations (C/R)

extracted

Concepts/relations benchmark

(BK)

defined not defined

produced by approach 63 26

in right

relation

in wrong

relation

47 16

not produced by approach 19

REFERENCES

Studer, R., Benjamins, V. R., Fensel, D., 1998.

Knowledge Engineering: Principles and methods.

Data & Knowledge Engineering, vol. 25, no. 1-2, pp.

161-197.

Kjellberg, T., von Euler-Chelpin, A., Hedlind, M.,

Lundgren, M., Sivard, G., Chen, D., 2009. The

machine tool model – A core part of the digital

factory. Annals of CIRP, vol. 58, no. 1, pp. 425-428.

Navigli, R., Velardi, P., Gangemi, A., 2003. Ontology

learning and its application to automated terminology

translation. Intelligent Systems, vol. 18, no. 1, pp. 22-

31.

Weng, S. S., Tsai, H. J., Liu, S. C., Hsu, C. H., 2006.

Ontology construction for information classification.

Expert Systems with Applications, vol. 31, no. 1, pp. 1-

12.

Toutanova, K., Manning, C. D., 2000. Enriching the

knowledge sources used in a maximum entropy part-

of-speech tagger. In Proceedings of Joint SIGDAT

Conference on Empirical Methods in Natural

Language Processing and Very Large Corpora, pp.

63-70.

Chow, T. W. S., Zhang, H., Rahman, M. K. M., 2009. A

new document representation using term frequency

and vectorized graph connectionists with application

to document retrieval. Expert Systems with

Application, vol. 36, no. 1, pp. 12023-12035.

Dongen, S. V., 2000. A Cluster Algorithm for graphs.

Technical Report INS-R0010, National Research

Institute for Mathematics and Computer Science in the

Netherlands, Amsterdam.

Yan, X. F., Han, J. W., 2002. gSpan: Graph-based

substructure pattern mining. In Proceedings of

International Conference on Data Mining, pp 721-

724.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

334