REASONING WITH THE FUZZY DESCRIPTION LOGIC f

Jidi Zhao

, Harold Boley

and Weichang Du

Faculty of Computer Science, University of New Brunswick, 540 Windsor Street, Fredericton, Canada

Institute for Information Technology, National Research Council of Canada, 46 Dineen Drive, Fredericton, Canada

Keywords:

Semantic web, Uncertain knowledge, Description logic, Fuzzy logic, Linear programming.

Abstract:

While applications in different areas have shown the necessity of dealing with uncertain knowledge, Semantic

Web techniques based on standard Description Logics do not have such a capability. Motivated by this discrep-

ancy, we introduce an expressive fuzzy description logic, f

SI , which extends the classic Description Logic

SI to deal with uncertain knowledge about concepts and roles as well as instances of concepts and roles. In the

family of Fuzzy Logics it is semantically based on Zadeh Logic, which naturally interprets uncertain knowl-

edge about concepts and roles as fuzzy sets and fuzzy relations, and interprets uncertain knowledge about

instances as elements with degrees of membership. The paper focuses on several reasoning methods for the

main reasoning problems in f

SI , including consistency checking, instance range entailment, and f-retrieval

problems.

1 INTRODUCTION

The Semantic Web initiative aims at creating an ex-

tension to the current World Wide Web by develop-

ing logic-based standards and technologies that en-

able machines to understand the information on the

Web, so that they can support richer knowledge infer-

ence and automate the performance of various tasks

for human beings (Berners-Lee et al., 2001).

The current W3C standard for Semantic Web on-

tology languages, Web Ontology Language (OWL),

is designed for use by applications that need to pro-

cess the content of information instead of just pre-

senting information to humans (McGuinness and van

Harmelen, 2004). It facilitates greater machine in-

terpretability of Web content than that supported by

other Web languages such as XML, RDF, and RDF

Schema (RDFS). This ability of OWL is enabled by

its underlying knowledge representation formalism of

Description Logics (DLs). DLs (Baader et al., 2003;

Horrocks and Sattler, 1999) are a family of logic-

based formalisms designed to represent and reason

about the conceptual knowledge of arbitrary domains.

Elementary descriptions of DLs are atomic concepts

and atomic roles. Complex concept descriptions and

role descriptions can be built from the elementary de-

scriptions according to construction rules. Different

description languages of DLs are distinguished by the

kind of concept and role constructors (such as conjun-

ction, disjunction, and exists restriction) allowed in

their description language and the kinds of axioms al-

lowed in their terminologies. The basic proposition-

ally closed DL is ALC in which the letters AL stand

for attributive language and the letter C for comple-

ment (negation of arbitrary concepts). Besides ALC,

other letters are used to indicate various DL exten-

sions. For example, in the Description Logic S I (Hor-

rocks and Sattler, 1999), S is used for ALC extended

with transitive roles (R

), and I for inverse roles. DLs

have a model-theoretic semantics, which is deﬁned by

interpreting concepts as sets of individuals and roles

as sets of pairs of individuals. An interpretation I is

a pair I = (∆

,·

) consisting of a domain ∆

which is

a non empty set and of an interpretation function ·

which maps each individual x into an element of ∆

(x ∈ ∆

), each concept C into a subset of ∆

⊆ ∆

)

and each role R into a subset of ∆

×∆

⊆ ∆

×∆

The semantics of complex concept and role descrip-

tions can be found in (Baader et al., 2003; Horrocks

and Sattler, 1999). Furthermore, a knowledge base

(KB) in DLs consists of two parts: the terminological

box (TBox T ) and the assertional box (ABox A).

Uncertainty is an intrinsic feature of real-world

knowledge, which is also reﬂected in the World Wide

Web and the Semantic Web. Many concepts needed in

knowledge modeling lack well-deﬁned boundaries or,

precisely deﬁned criteria. Examples are the concepts

of young, tall, and cold. The Uncertainty Reason-

Zhao J., Boley H. and Du W..

REASONING WITH THE FUZZY DESCRIPTION LOGIC fZSI.

DOI: 10.5220/0003054700210030

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICFC-2010), pages

21-30

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

ing for the World Wide Web (URW3) Incubator Group

deﬁned the challenge of representing and reasoning

with uncertain information on the Web. According

to the latest URW3 draft report, uncertainty is a term

intended to encompass different forms of uncertain

knowledge, including incompleteness, inconclusive-

ness, vagueness, ambiguity, and others (Laskey et al.,

2008). The need to model and reason with uncer-

tainty has been found in many different Semantic

Web contexts, such as matchmaking in Web services

(Martin-Recuerda and Robertson, 2005), classiﬁca-

tion of genes in bioinformatics (Stevens et al., 2007),

multimedia annotation (Stamou et al., 2006), and on-

tology learning (Haase and V

olker, 2005).

Fuzzy Set Theory was ﬁrst introduced by Zadeh

(Zadeh, 1965) as an extension to the classic notion of

a set to capture inherent vagueness (the lack of crisp

boundaries of sets). Fuzzy Logic is a form of multi-

valued logic derived from Fuzzy Set Theory to deal

with reasoning that is approximate rather than precise.

In Fuzzy Logic, the degree of truth of a statement can

range between 0 and 1, and is not constrained to the

two truth values {0,1} or { f alse,true} as in classic

predicate logic. Formally, a fuzzy set A with respect

to a set of elements Ω (also called a universe) is char-

acterized by a membership function µ

(x) which as-

signs a value in the real unit interval [0,1] to each ele-

ment x in Ω (x ∈ Ω), notated as µ

: Ω → [0,1]. µ

(x),

often written as A(x), gives the degree of an element x

belonging to the set A. Such degrees can be computed

based on a membership function. A fuzzy relation R

over two fuzzy sets A and B is similarly deﬁned by a

function R : Ω × Ω → [0, 1].

Fuzzy Logic extends the Boolean operations de-

ﬁned on crisp sets and relations for fuzzy sets and

fuzzy relations. These operations, e.g. complement,

union, and intersection, are interpreted as mathemat-

ical functions over the unit interval [0,1]. In the fol-

lowing, η,θ deﬁne the truth degrees of sets and re-

lations, ranging between 0 and 1. The mathemati-

cal functions for fuzzy intersection are usually called

t-norms (t(η,θ)); those for fuzzy union are called

s-norms (s(η,θ), a.k.a. t-conorms); and those for

the fuzzy set complement are called negations (¬η);

These functions usually satisfy certain mathematical

properties. The most widely known operations in the

Fuzzy Logic family are Zadeh Logic, Lukasiewicz

Logic, Product Logic, and G

odel Logic.

To deal with the ‘crisp limitation’ of classic DLs,

considerable work has been carried out on integrating

uncertain knowledge into DLs in recent years. The

current literature generally follows two approaches.

One is Probabilistic Logic based on Probability The-

ory; for example the work in (Jaeger, 1994; Koller

et al., 1997; Lukasiewicz, 2008). The other is Fuzzy

Logic and Fuzzy Sets; for example the work in (Yen,

1991; Straccia, 2001; Zhao and Boley, 2010). A re-

view and comparison of these works can be found in

(Zhao, 2010). We presented a Norm-Parameterized

Fuzzy Description Logic fALC N and addressed the

consistency checking problem in (Zhao and Boley,

2010). We use f

DL to denote a Fuzzy Descrip-

tion Logic fDL with norm parameter N. Omitting

the index N means the fDL is norm-parameterized.

In the current paper, we follow the Fuzzy Sets and

Fuzzy Logic approach and present the fuzzy Descrip-

tion Logic f

SI . We call this fuzzy Description Logic

SI as S I is the underlying Description Logic and Z

ﬁxes the norms to Zadeh Logic. This paper is differ-

ent from previous work due to the following features.

First, the underlying classic DL S I is a more expres-

sive Description Logic which deals with fuzzy transi-

tive roles and fuzzy inverse roles. Second, we com-

bine Description Logic, Fuzzy Logic, and Linear Pro-

gramming methods in the reasoning procedure. Last

but not least, f

SI supports both fuzzy axioms and

fuzzy assertions for uncertain knowledge representa-

tion and reasoning.

2 THE FUZZY DL f

SI extends the f

ALC N DL with inverse roles,

and transitive roles but excludes number restrictions.

Due to space limitations, we refer interested readers

to (Zhao and Boley, 2010) for the syntax and seman-

tics of complex concept descriptions as well as ax-

ioms and assertions for f

ALC by specializing the

t-norm to min and the s-norm to max. Here we sim-

ply list them in Tables 1 and 2, and then explain the

expressiveness beyond f

ALC . A fuzzy knowledge

base in f

SI consists of two parts: the fuzzy termino-

logical box consisting of a ﬁnite set of fuzzy axioms

(TBox T ) and the fuzzy assertional box consisting of

a ﬁnite set of fuzzy assertions (ABox A). As shown

in Table 2, a fuzzy axiom or fuzzy assertion is of the

form α [l,u] with 0 ≤ l ≤ u ≤ 1, which is equivalent to

the two inequalities α ≥ l and α ≤ u. In what follows,

we use these expressions as needed.

In classic DLs, a role R is symmetric iff for all

x,y ∈ 4

, (Inv(R))

(y,x) = R

(x,y), where the role

function Inv(R) deﬁnes the inverse of a role. The

same property holds for a fuzzy symmetric role. For

example, the role hasPart is the inverse of the role

isPartOf.

In classic DLs, a role R is transitive iff for all

x,y,z ∈ 4

, R

(x,y) and R

(y,z) imply R

(x,z). While

in Fuzzy Logic, a fuzzy role R is transitive iff for all

ICFC 2010 - International Conference on Fuzzy Computation

Table 1: Syntax and semantics of f

SI constructors.

Constructor Syntax Semantics

top concept > >

= 1

bottom

concept

⊥ ⊥

= 0

atomic

negation

¬A (¬A)

(x) = 1 − A

(x)

concept

conjunction

C uD (C u D)

= min(C

(x),D

(x))

concept

disjunction

C tD (C t D)

= max(C

(x),D

(x))

exists

restriction

∃R.C (∃R.C)

(x) =

sup

y∈∆

{min(R

(x,y),C

(y))}

value

restriction

∀R.C (∀R.C)

(x) = inf

y∈∆

{max(1 −

(x,y),C

(y))}

inverse role Inv(R) (Inv(R))

(y,x) = R

(x,y)

Table 2: Syntax and semantics of f

SI axioms.

Axioms Syntax Semantics

concept

inclusion

A v C ∀x ∈ ∆

(x) ≤ C

(x)

concept

deﬁnition

A ≡ C ∀x ∈ ∆

(x) = C

(x)

concept

implica-

tion

A →

C [l,u]

∀x ∈ ∆

(x) ∈

min(A

(x),[l,u])

transitive

role

Trans(R) R

(a,c) ≥

sup

b∈4

min(R

(a,b),R

(b,c))

concept

assertion

C(a) [l,u] l ≤ C

(a) ≤ u

role asser-

tion

R(a,b) [l, u] l ≤ R

(a,b) ≤ u

individual

inequality

a 6= b a

6= b

x,y,z ∈ 4

, it satisﬁes the following inequality (D

ıaz

et al., 2010):

(x,z) ≥ sup

y∈4

t(R

(x,y),R

(y,z)) (1)

where t(η,θ) denotes a general t-norm. Thus, in the

case of Zadeh Logic, a transitive role satisﬁes:

(x,z) ≥ sup

y∈4

min(R

(x,y),R

(y,z)) (2)

In order to make the following explanations eas-

ier, we introduce the role function Trans(R) which

speciﬁes that R is transitive or Inv(R) is transitive.

Now, we use some mathematical properties of

Zadeh Logic to show that the following property

is satisﬁed by a role value restriction ∀R.C with

Trans(R).

Lemma 1. Under Zadeh Logic, if (∀R.C)

(x) ≥ l (l ∈

[0,1]) and R is transitive, then (∀R.(∀R.C))

(x) ≥ l

holds.

Proof. (∀R.C)

(x) ≥ l

De f inition o f semantics

−−−−−−−−−−−−−−→

inf

z∈∆

{max(¬R

(x,z),C

(z))} ≥ l

Equation 1

−−−−−−→

inf

z∈∆

inf

y∈∆

{max(¬(min(R

(x,y),R

(y,z))),C

(z))} ≥ l

De Morgan

s Law

−−−−−−−−−−→

inf

z∈∆

inf

y∈∆

{max(max(¬R

(x,y),¬R

(y,z)),C

(z))} ≥ l

Associativity

−−−−−−−→

inf

z∈∆

inf

y∈∆

{max(¬R

(x,y),max(¬R

(y,z),C

(z)))} ≥ l

Commutativity

−−−−−−−−→

inf

y∈∆

{max(¬R

(x,y),inf

z∈∆

max(¬R

(y,z),C

(z)))} ≥ l

De f inition o f semantics

−−−−−−−−−−−−−−→

inf

y∈∆

{max(¬R

(x,y),(∀R.C)

(y))} ≥ l

De f inition o f semantics

−−−−−−−−−−−−−−→ (∀R.(∀R.C))

(x) ≥ l

However, in the cases of ≤, we cannot derive such

a property for (∀R.C)(x) and Trans(R).

Under Zadeh Logic, by applying the semantics of

∃R.C and negation, it is easy to see that the following

equivalence rules hold:

∀a,b ∈ ∆

¬¬C ≡ C , (3)

¬∃R.C ≡ ∀R.¬C , (4)

¬∀R.C ≡ ∃R.¬C (5)

Then, (∃R.C)

(x) ≤ u

Monotonicity

−−−−−−−→ ¬((∃R.C)

(x)) ≥ 1 − u

Equilvalence 4

−−−−−−−−→ (∀R.(¬C))

(x)) ≥ 1 − u

Lemma 1

−−−−−→ (∀R.(∀R.(¬C)))

(x)) ≥ 1 − u

Monotonicity

−−−−−−−→ ¬(∀R.(∀R.(¬C))

(x)) ≤ u

Equilvalence 5

−−−−−−−−→ (∃R.¬(∀R.(¬C)))

(x) ≤ u

Equilvalence 5 and 3

−−−−−−−−−−−−→ (∃R.(∃R.C))

(x) ≤ u

Therefore, the following property is satisﬁed with

respect to a role exists restriction ∃R.C and Trans(R).

Such a property cannot be inferred from the cases of

≥.

Lemma 2. Under Zadeh Logic, if (∃R.C)

(x) ≤ u and

R is transitive, then (∃R.(∃R.C))

(x) ≤ u holds.

Although we can show that such properties also

hold under Product Logic and other logics, we ne-

glect it here, as it is out of scope. We will soon see

that these properties will be embodied in the fuzzy

completion rules for the f

SI reasoning algorithm.

REASONING WITH THE FUZZY DESCRIPTION LOGIC fZSI

3 REASONING ALGORITHM

FOR BUILDING A FUZZY

TABLEAU OF f

The reasoning algorithm that we will present is a

fuzzy extension to the tableau method and tests the

consistency of a knowledge base KB =< T , A > by

trying to construct a model of KB. A model of KB

in our Fuzzy Description Logic f

SI is a fuzzy in-

terpretation I = (4

,·

). Similar to the classic DL,

such a model has the shape of a forest, i.e., a col-

lection of trees, with nodes corresponding to indi-

viduals, root nodes corresponding to named individ-

uals, and edges corresponding to roles between indi-

viduals. Each node has a node label L(individual),

but different from classic DLs, each node in a f

tableau is labeled with a set of f

SI -concepts. Each

element in the set consists of a pair of elements

{concept,constraint}. The sets for all nodes are re-

stricted to subsets of sub(A), where sub(A) is the

set of sub-concepts of concepts that appear within an

ABox A. Furthermore, each edge is associated with

an edge label L(individual

, individual

) which con-

sists of a pair of elements {role,constraint}.

In (Zhao and Boley, 2010), we explained the TBox

processing procedure which consists of some prepro-

cessing steps to deal with the fuzzy TBox before ap-

plying the reasoning algorithm. Those steps are appli-

cable to the f

SI knowledge base. Therefore, we can

assume all concepts C occurring in KB to be in nega-

tion normal form (NNF) and we only deal with un-

foldable TBox after those preprocessing steps. How-

ever, due to the properties of a f

SI knowledge base,

the TBox processing procedure should include a cou-

ple of other steps. First, the TBox processing proce-

dure transforms all the assertions in the fuzzy ABox

and the fuzzy implication axioms in the fuzzy TBox

with the form α

[l, u] into two expressions: α

≥ l

and α

≤ u. In order to keep our presentation simple

and compact, in what follows, we use a general form

α op n where op ∈ {≥, ≤} and n ∈ [0,1] whenever

applicable. Second, an f

SI knowledge base may

contain transitive role axioms and inverse roles. We

know that if a role R is transitive, the inverse role of R

is also transitive. Therefore, for each pair of Trans(R)

and Inv(R), the procedure should also add an axiom

Trans(Inv(R)). After the application of the TBox pro-

cessing procedure, in what follows, we only have to

consider a knowledge base in f

SI only consists of

fuzzy ABox assertions, a set of transitive role axioms,

and a ﬁnite set of fuzzy implication axioms.

Next, we ﬁrst present the deﬁnitions of fuzzy

tableau, clash, and clash-free, and then prove the rela-

tion between the consistency of a fuzzy knowledge

base KB =< T ,A > and the existence of a fuzzy

tableau T for KB.

Deﬁnition 1. If KB =< T ,A > is an f

SI knowledge

base, R

is the set of roles occurring in A, together

with their Inv(R)s, a fuzzy tableau T for KB is deﬁned

to be a quadruple (S, L, ε,C ) such that: S is a set of

individuals, L : S × sub(A) → [0,1] maps each indi-

vidual and a concept which is a subset of sub(A) to

the membership degree of the individual to that con-

cept, ε : R

×S ×S → [0, 1] maps each role in R

and

a pair of individuals to the membership degree of the

pair to the role, and C is a set of constraints must be

satisﬁed. For all x,y ∈ S, A,C,D ∈ sub(A), R ∈ R

and n ∈ [0, 1], it holds that:

1. For any x ∈ S, {x : ⊥ = 0} and {x : > = 1} ∈ L(x).

2. If {x : ¬(A) op n} ∈ L(x), then {x : A op 1 − n} ∈

L(x).

3. If {x : C uD ≥ n} ∈ L(x), then {x : C ≥ n} ∈ L(x)

and {x : D ≥ n} ∈ L(x).

4. If {x : C tD ≤ n} ∈ L(x), then {x : C ≤ n} ∈ L(x)

and {x : D ≤ n} ∈ L(x).

5. If {x : C u D ≤ n} ∈ L(x), then {x : C ≤ n

} ∈

L(x), {x : D ≤ n

} ∈ L(x), and n = min(n

)

for some n

6. If {x : C t D ≥ n} ∈ L(x), then {x : C ≥ n

} ∈

L(x), {x : D ≥ n

} ∈ L(x), and n = max(n

)

for some n

7. If {x : ∃R.C ≥ n} ∈ L(x), then there exists y ∈ S

such that {< x, y >: R ≥ n} ∈ ε(R) and {y : C ≥

n} ∈ L(y).

8. If {x : ∀R.C ≤ n} ∈ L(x), then there exists y ∈ S

such that {< x, y >: R ≥ 1 − n} ∈ ε(R) and {y :

C ≤ n} ∈ L(y).

9. If {x : ∃R.C ≤ n} ∈ L(x), then {< x,y >: R ≤

} ∈ ε(R), {y : C ≤ n

} ∈ L(y), and n =

min(n

) for some n

10. If {x : ∀R.C ≥ n} ∈ L(x), then {< x,y >: R ≤ 1 −

} ∈ ε(R), {y : C ≥ n

} ∈ L(y), and n = max(1−

) for some n

11. {< x, y >: R op n} ∈ ε(R) iff {< y,x >:

Inv(R) op n} ∈ ε(R).

12. If {x : ∀R.C ≥ n} ∈ L(x) and Trans(R), then

{< x,y >: R ≤ 1 − n

} ∈ ε(R), {y : ∀R.C ≥ n

} ∈

L(y), and n = max(1 − n

) for some n

13. If {x : ∃R.C ≤ n} ∈ L(x) and Trans(R), then {<

x,y >: R ≤ n

} ∈ ε(R), {y : ∃R.C ≤ n

} ∈ L(y),

and n = min(n

) for some n

14. If {A → C ≥ n} ∈ T and {x : A ≥ n

} ∈ L(x),

then {x : C ≥ n

} ∈ L(x) and n

= min(n,n

for any x ∈ S.

ICFC 2010 - International Conference on Fuzzy Computation

15. If {A → C ≤ n} ∈ T and {x : A ≤ n

} ∈ L(x),

then {x : C ≤ n

} ∈ L(x) and n

= min(n,n

for any x ∈ S.

In (Zhao and Boley, 2010), we deﬁned the se-

mantics (C u D)

as t(C

(x),D

(x)) for various t-

norms. For the case of Zadeh Logic, we have that

if (C u D)

(x) ≥ n, then C

(x) = n

, D

(x) = n

, and

min(n

) ≥ n. In this deﬁnition, we can draw a

further conclusion based on the properties of the min

norm that C

(x) = n

≥ n and D

(x) = n

≥ n. Sim-

ilar extensions are conducted on other f

SI concepts

and roles.

Deﬁnition 2. Let A be an extended f

SI ABox, A

contains a clash if only if one of the following situa-

tions occurs:

1. {⊥(a) 6= 0} ⊆ A

2. {>(a) 6= 1} ⊆ A

3. {α ≤ n

,α ≥ n

} ⊆ A and n

< n

4. there is no solution for the constraint system of

inequations C

A is called clash-free if it does not contain any clash.

Lemma 3. An f

SI knowledge base KB =< T ,A >

is consistent iff there exists a clash-free fuzzy tableau

for KB.

Proof. For the if direction, if T=(S,L,ε) is a clash-

free fuzzy tableau for a fuzzy knowledge base KB, a

fuzzy interpretation I=(∆

,·

) can be constructed as:

∆

= S

={x : > = 1} ∈ L(x) for any x in S

⊥

={x : ⊥ = 0} ∈ L(x) for any x in S

={x : A op n} ∈ L(x) for all concept names A in

sub(A)

(

ε(R)

i f Trans(R)

ε(R) otherwise

where ε(R)

denotes the fuzzy sup-min transitive

closure of ε(R) (Lee, 2001; Mitsuishi and Bancerek,

2003).

To prove that I is a model of KB, we show by

induction on the structure of concepts that, if {x :

E op n} ∈ L(x), then E

(x) op n for any x in S. With-

out loss of generality, we only show in the following

the cases with {x : E ≥ n} ∈ L(x).

1. If E the > or ⊥ concept, and {x : ⊥ = 0} and

{x : > = 1} ∈ L(x), then by deﬁnition, >

(x) = 1

or ⊥

(x) = 0.

2. If E is a concept name other than > and ⊥, and

{x : E ≥ n} ∈ L(x), then E

(x) ≥ n by deﬁnition.

3. If E = ¬(C) and {x : ¬(C) ≥ n} ∈ L(x), then {x :

C ≤ 1−n} ∈ L(x) (due to Property 2 in Deﬁnition

1), so we have C

(x) ≤ 1− n by induction. Hence,

(¬C)

(x) ≥ 1 − (1 − n) = n, i.e., E

(x) ≥ n.

4. If E = (C

) and {x : C

≥ n} ∈ L(x), then

{x : C

≥ n} ∈ L(x) and {x : C

≥ n} ∈ L(x), so by

induction (C

)

(x) ≥ n and (C

)

(x) ≥ n. Hence,

)

(x) = min((C

)

(x),(C

)

(x)) ≥ n.

5. If E = (C

t C

) and {x : C

t C

≥ n} ∈ L(x),

since the tableau is clash free, we can ﬁnd some

so that {x : C

≥ n

} ∈ L(x), {x : C

≥

} ∈ L(x) and n = max(n

). By induc-

tion (C

)

(x) ≥ n

, (C

)

(x) ≥ n

. Hence, (C

)

(x) = max((C

)

(x),(C

)

(x)) ≥ n.

6. If E = (∃S.C) and {x : ∃S.C ≥ n} ∈ L(x), then

there exists y ∈ S such that {< x,y >: S ≥ n} ∈

ε(S) and {y : C ≥ n} ∈ L(y), so by induction

(x,y) ≥ n and C

(y) ≥ n. Hence (∃S.C)

(x) =

sup

y∈∆

min(S

(x,y),C

(y)) ≥ n.

7. If E = (∀S.C), {x : ∀S.C ≥ n} ∈ L(x), and

(x,y) = m, then it would be either of the fol-

lowing two cases.

• {< x, y >: S = m} ∈ ε(S): if m > 1 − n, then

{y : C ≥ n} ∈ L(y) (due to Property 10 in Def-

inition 1), so we have S

(x,y) > 1 − n and

(y) ≥ n, hence, (∀S.C)

(x) = in f

y∈∆

max(1−

(x,y),C

(y)) ≥ n; if m <= 1 − n, then 1 −

(x,y) = 1 − m ≥ n, hence (∀S.C)

(x) =

in f

y∈∆

max(1 − S

(x,y),C

(y)) ≥ n.

• {< x, y >: S = m} /∈ ε(S) and there exist l paths

(l ≥ 1) such that in each path, {< x,x

>: S =

} ∈ ε(S), {< x

>: S = m

} ∈ ε(S), · ··,

{< x

,y >: S = m

l(n+1)

} ∈ ε(S) and Trans(R).

Thus, the truth degree of < x,y > to the tran-

sitive closure of S, m, would be equal to the

supremum value among all the minimum val-

ues of each path. In this case: if m > 1 − n,

then there exists at least one path k, {< x, x

S = m

} ∈ ε(S), {< x

>: S = m

} ∈

ε(S), ·· ·, {< x

,y >: S = m

k(n+1)

} ∈ ε(S), we

have m

> m > 1 − n (1 ≤ i ≤ (n + 1)) (as

m is the minimum value of the path), {x

(∀S.C) ≥ n} ∈ L(x

) (1 ≤ i ≤ n), and {y :

(∀S.C) ≥ n} ∈ L(y) (due to Property 12 in Def-

inition 1), so, inducted from {< x, x

>: S >

1 − n} ∈ ε(S) and {x

: (∀S.C) ≥ n} ∈ L(x

we have S

(x,x

) > 1 − n and (∀S.C)

) ≥

n, and thus C

) ≥ n, hence (∀S.C)

(x) =

in f

y∈∆

max(1 − S

(x,x

),C

)) ≥ n; if

m <= 1 − n, then we have max(1−m,C

(y)) ≥

n, hence (∀S.C)

(x) ≥ n.

The cases for the ≤ inequalities can be proved in

a similar way.

For the converse, if I=(∆

,·

) is a model of A, then

a fuzzy tableau T=(S,L,ε) can be deﬁned as:

S = ∆

REASONING WITH THE FUZZY DESCRIPTION LOGIC fZSI

ε(R) = R

L(x) = {x : C op n} for all x ∈ S and C ∈ sub(A)

To prove that T is a fuzzy tableau of KB, we show

that, based on I, all the properties in Deﬁnition 1 are

satisﬁed.

1. T satisﬁes Property 1 - 12, 14, and 15 as a di-

rect consequence of the semantics of f

SI con-

cepts. For example, let {x : C u D ≥ n} ∈ L(x),

the semantics of fuzzy concept conjunction im-

plies that (C u D)

(x) = min(C

(x),D

(x)) ≥ n,

thus we have D

(x) ≥ n and D

(x) ≥ n, that is,

{x : C ≥ n} ∈ L(x) and {x : D ≥ n} ∈ L(x), hence

Property 3 is satisﬁed. For similar reasons, other

properties hold.

2. Property 12 of Deﬁnition 1 is satisﬁed as a re-

sult of the semantics and the properties of tran-

sitive roles and value restrictions that have been

investigated in Section 2. Hence, if (∀R.C)

(x) ≥

n, Trans(R) then (∀R.(∀R.C))

(x) ≥ n, thus

(s,t) ≤ 1 − n

, (∀R.C)

(t) ≥ n

and n =

max(1 − n

) hold.

3. Similarly, Property 13 is satisﬁed as a result of

the semantics and the properties of transitive roles

and role exists restrictions.

From Lemma 3, an algorithm that constructs a

fuzzy tableau for an f

SI knowledge base can be used

as a decision procedure for the consistency checking

problem.

Similar to the tableau algorithm presented by Hor-

rocks et al. (Horrocks et al., 2000), our algorithm

works on building a fuzzy tableau for an f

SI knowl-

edge base which may be a completion-forest since

the ABox might contain several named individuals

with arbitrary edges connecting them. Each node x

is labeled with a set L(x) = {{x : C

op n

},·· · ,{x :

op n

}} (m ≥ 1) and a constraint set C (x) =

{{x

op n

},·,{x

op n

}}, where C

∈ sub(A),

∈ [0,1], 1 ≤ i ≤ m, and op ∈ {≥,≤}. Each edge

< x,y > is labeled with a set L(x,y) = {[x,y] : R op n}

and a constraint in the set C (x, y) = {x

op n}, where

R are roles occurring in A.

We adapt the conjugation concept in (Straccia,

2001) to represent pairs of fuzzy assertions that form

a contradiction. Let α be a SI assertion, two fuzzy as-

sertions (α ≥ n

and α ≤ n

) conjugate with each

other if n

> n

. For a given fuzzy assertion, its conju-

gated assertion is not unique, and in fact, inﬁnite. For

example, both {[x,y] : R ≤ 0.5} and {[x,y] : R ≤ 0.3}

conjugate with the fuzzy assertion {[x,y] : R ≥ 0.6}.

Let us recall some notations used in (Horrocks

and Sattler, 1999). If nodes x and y are connected

by an edge < x,y > with {R op n} ∈ L(x,y), then y

is called an R

-successor of x and x is called an R

predecessor of y. Ancestor is the transitive closure of

predecessor. If y is an R

-successor or an (Inv(R))

predecessor of x, then y is called an R

-neighbor of

x. An expressive DL such as f

SI which allows tran-

sitive roles and inverse roles may lead to nontermina-

tion as the fuzzy completion rules can introduce new

concepts that are the same size as the decomposed

concept. Our algorithm for the consistency check-

ing of an f

SI knowledge base follows the dynamic

blocking presented in (Horrocks and Sattler, 1999)

and uses it to guarantee the termination of the reason-

ing algorithm. In dynamic blocking, blocked nodes

are allowed to be dynamically established and broken

as the expansion progresses, and expand role value re-

striction and role exists restriction concepts. This dy-

namic blocking strategy is crucial in the presence of

inverse roles since information might be propagated

up the completion-forest and affect other branches.

For example, consider the nodes x, y and z, the edges

< x,y > and < x, z >. Suppose x blocks y. In the

presence of inverse roles it is possible that z adds in-

formation to node x, although z is a successor of x.

In that case the block on y must be broken. A node

x is blocked if for some ancestor y, y is blocked or

L(x) = L(y). Dynamic blocking uses the notions of

directly blocked and indirectly blocked nodes. If a

blocked node x’s predecessor is blocked, x is called

indirectly blocked. A blocked node x is called di-

rectly blocked if it has a unique ancestor y such that

L(x) = L(y).

Now, for an expanded f

SI ABox A with a set of

transitive role axioms and a set of fuzzy implication

axioms, the algorithm initializes a forest to contain

(1)root nodes, for each individual x occurring in A,

the root node x is labeled with L(x) = {x : C op n}

and C (x) = {x

op n} for each assertion of the form

C(x) op n in A, and (2)edges, each edge hx, yi cor-

responds to an assertion R(x,y) op n in A with R be

an atomic role or an inverse role and is labeled with

L(x, y) = {[x,y] : R op n} and C (x,y) = {x

op n}. If

an assertion is of the form Inv(P)(x,y) op n, the cor-

responding edge is also labeled with L(x,y) = {[y, x] :

P op n} and C(x,y) = {x

op n}. The completion for-

est is then expanded by repeatedly applying the fol-

lowing fuzzy completion rules in Table 3. The com-

pletion forest is complete when a clash is detected, or

none of the fuzzy completion rules are applicable.

ICFC 2010 - International Conference on Fuzzy Computation

Table 3: Fuzzy Completion Rules for f

SI Fuzzy Completion Rules

≥

-rule

Condition: {x : (¬A) ≥ n} ∈ L(x) and {x : A ≤ 1 − n} /∈ L(x)

Action: L(x) −→ L(x) ∪ {{x : A ≤ 1 − n}} and C (x) −→ C (x) ∪ {x

≤ (1 − n)}

≤

-rule

Condition: {x : (¬A) ≤ n} ∈ L(x) and {x : A ≥ 1 − n} /∈ L(x)

Action: L(x) −→ L(x) ∪ {{x : A ≥ 1 − n}} and C (x) −→ C (x) ∪ {x

≥ (1 − n)}

≥

-rule

Condition: {x : (C

) ≥ n} ∈ L(x), x is not indirectly blocked, and {{x : C

≥ n},{x : C

≥ n}} * L(x)

Action: L(x) −→ L(x) ∪ {{x : C

≥ n},{x : C

≥ n}} and C (x) −→ C(x) ∪ {x

≥ n,x

≥ n}

≤

-rule

Condition: {x : (C

) ≤ n} ∈ L(x), x is not indirectly blocked, and {{x : C

≤ n},{x : C

≤ n}} ∩ L(x) = ∅

Action: L(x) −→ L(x) ∪ {{x : C

≤ x

},{x : C

≤ x

}} and C (x) −→ C(x) ∪ {x

≤ x

+ x

= 1 + n,x

≥ y,x

≥ 1 − y, y ∈ {0,1},x

∈

[0,1],x

∈ [0,1]}

≥

-rule

Condition: {x : (C

) ≥ n} ∈ L(x), x is not indirectly blocked, and {{x : C

≥ n},{x : C

≥ n}} ∩ L(x) = ∅

Action: L(x) −→ L(x) ∪{{x : C

≥ x

},{x : C

≥ x

}} and C(x) −→ C (x) ∪ {x

≥ x

= n, x

≤ y,x

≤ 1 − y, y ∈ {0, 1},x

∈ [0, 1], x

∈

[0,1]}

≤

-rule

Condition: {x : (C

) ≤ n} ∈ L(x), x is not indirectly blocked, and {{x : C

≤ n},{x : C

≤ n}} * L(x)

Action: L(x) −→ L(x) ∪ {{x : C

≤ n},{x : C

≤ n}} and C (x) −→ C(x) ∪ {x

≤ n,x

≤ n}

∃

≥

-rule

Condition: {x : (∃R.C) ≥ n} ∈ L(x), x is not blocked, and x has no R

-neighbor y

Action: create a new node y with L(x,y) = {{[x,y] : R ≥ n}}, L(y) = {{y : C ≥ n}}, C (x,y) = {x

≥ n}, and C(y) = {x

≥ n}

∃

≤

-rule

Condition: {x : (∃R.C) ≤ n} ∈ L(x), x is not indirectly blocked, and x has an R

-neighbor y with {[x,y] : R op n1} ∈ L(x,y) and {y : C ≤ n} /∈ L(y).

Action: L(y) −→ L(y) ∪ {{y : C ≤ n}}, if {[x,y] : R op n1} conjugates with {[x,y] : R ≤ n}, then C (y) −→ C (y) ∪ {x

≤ n}, else C(y) −→ C (y) ∪{x

≤

n,n

> n}

∀

≥

-rule

Condition: {x : (∀R.C) ≥ n} ∈ L(x), x is not indirectly blocked and x has an R

-neighbor y with {y : C ≥ n} /∈ L(y)

Action: L(y) −→ L(y) ∪ {{y : C ≥ n}}, if {[x,y] : R op n1} conjugates with {[x,y] : R ≤ (1 − n)}, then C (y) −→ C (y) ∪ {x

≥ n}, else C(y) −→

C (y) ∪ {x

≥ n,n1 > 1 − n}

∀

≤

-rule

Condition: {x : (∀R.C) ≤ n} ∈ L(x), x is not blocked, x has no R

-neighbor y, and {y : C ≤ n} ∈ L(y)

Action: create a new node y with L(x,y) = {{[x,y] : R ≥ (1 − n)}}, L(y) = {{y : C ≤ n}}, C (x,y) = {x

≥ (1 − n)}, and C (y) = {x

≤ n}

∃

≤,+

-rule

Condition: {x : (∃R.C) ≤ n} ∈ L(x), Trans(R), x is not indirectly blocked, and x has an R

-neighbor y with {y : (∃R.C) ≤ n} /∈ L(y)

Action: L(y) −→ L(y) ∪ {{y : (∃R.C) ≤ n}}, if {[x, y] : R op n1} conjugates with {[x, y] : R ≤ n}, then C (y) −→ C (y) ∪ {x

∃R.C

≤ n}, else C (y) −→

C (y) ∪ {x

∃R.C

≤ n,n1 > n}

∀

≥,+

-rule

Condition: {x : (∀R.C) ≥ n} ∈ L(x), Trans(R), x is not indirectly blocked, and x has an R

-neighbor y with {y : (∀R.C) ≥ n} /∈ L(y)

Action: L(y) −→ L(y) ∪ {{y : (∀R.C) ≥ n}}, if {[x,y] : R op n1} conjugates with {[x, y] : R ≤ (1 − n)}, then C (y) −→ C (y) ∪ {x

∀R.C

≥ n}, else C (y) −→

C (y) ∪ {x

∀R.C

≥ n,n1 > 1 − n}

→

≥

-rule

Condition: {A → C ≥ n} ∈ T , {x : A ≥ n

} ∈ L(x)

Action: L(x) −→ L(x) ∪ {{x : D ≥ n

}} and C (x) −→ C(x) ∪ {x

≥ n

= min(n,n

)}

→

≤

-rule

Condition: {A → C ≤ n} ∈ T , {x : A ≤ n

} ∈ L(x)

Action: L(x) −→ L(x) ∪ {{x : D ≤ n

}} and C (x) −→ C(x) ∪ {x

≤ n

= min(n,n

)}

REASONING WITH THE FUZZY DESCRIPTION LOGIC fZSI

The algorithm stops when a clash occurs; KB is

consistent iff the completion rules can be applied in

such a way that they yield a complete and clash-free

completion forest, and KB is inconsistent otherwise.

Example 1. Consider a fuzzy knowledge base

KB = { CP → ∃hP.CP [0.5,1], CP(P002) [0.6,1],

(∃hP.CP)(P002) [0,0.4]} where we abbreviate the

concept CancerPatient and the role hasFirstDe-

greeRelatives by CP and hP, respectively. The knowl-

edge base describes that the truth degree for a ﬁrst-

degree relative of a cancer patient also being a cancer

patient is greater than or equal to 0.5. Person P002 is

a cancer patient with certainty greater than 0.6 and

the possibility that one of P002’s ﬁrst-degree relative

is also a cancer patient is less than or equal to 0.4.

The query is that whether KB is consistent or not.

First, because of the fuzzy concept implica-

tion axiom, {∃hP.CP(P002) [0.5,1]} is added to

A. Next, we can initialize the fuzzy tableau

by creating a node P002 and label it with

L(P002) = {{P002 : CP ≥ 0.6},{P002 : ∃hP.CP ≥

0.5},{P002 : ∃hP.CP ≤ 0.4}} and C(P002) = {x

≥

0.6,x

∃hP.CP

≥ 0.5, x

∃hP.CP

≤ 0.4}}. Since both {P002 :

∃hP.CP ≥ 0.5} and {P002 : ∃hP.CP ≤ 0.4} are con-

tained in the fuzzy tableau, the reasoning algorithm

obviously detects a clash. Therefore, it stops the ap-

plication of any fuzzy completion rule and returns that

KB is inconsistent.

Next, let us look at an example for the ∀

≥,+

-rule.

Example 2. Consider there are two as-

sertions in a fuzzy knowledge base:

(∀hasFriend.Student)(John) [0.75,1] and

hasFriend(John, Mary) [0.7,1] where hasFriend is a

transitive role.

Following the preprocessing steps, we have

{John : (∀hasFriend.Student) ≥ 0.75} ∈ L(John)

and {[John,Mary] : hasFriend ≥ 0.7}. Since

{[John, Mary] : hasFriend ≥ 0.7} conjugates with

{[John, Mary] : hasFriend ≤ 0.25}, the ∀

≥,+

-rule

is applicable, thus {Mary : (∀hasFriend.Student) ≥

0.75} is added to L(Mary).

We can see from Table 3 that all these fuzzy com-

pletion rules are based on the properties and the se-

mantics of f

SI concepts. Notice that since we as-

sume all concepts to be in their negation normal form,

the fuzzy concept negation rule only applies to con-

cept names.

Let us take a second look at the t

≥

-rule and the

≤

-rule. The t

≥

-rule generates several new con-

straints {x

= n, x

≤ y, x

≤ 1 −y, y ∈ {0, 1},x

∈

[0,1],x

∈ [0,1]}. We can see that y is an integer vari-

able with value of 0 or 1. When y = 0, we have

= 0, x

= n, and thus {x

≥ 0,x

≥ n}; while

y = 1, we have x

= n, x

= 0, and thus {x

≥ n,x

≥

0}. These two cases are actually representing the or-

branch of the concept disjunction rule in classic DL.

That is, the {0,1} integer variable y enable the sim-

ulation of or-branching. Furthermore, by the intro-

duction of the variable y, we also transform the non-

linear constraint max(x

) ≥ n into a set of linear

constraints. Similar conclusions can be drawn on the

≤

-rule. Now we can see that all the fuzzy comple-

tion rules in Table 3 generate only linear constraints,

therefore, the resulted constraint set for any node or

edge is a linear constraint set. Such a property makes

it possible for the reasoning algorithm to call some

external Linear Programming solver to solve the con-

straint set.

Here is another example to explain how the rea-

soning algorithm determines the consistency of a

knowledge base.

Example 3. Consider the following fuzzy knowledge

base KB = {Trans(R), C(a) [0.7,1], D(b) [0.8,1],

R(a,b) [0.6,1], R(b,c) [0.7,1], (∃Inv(R).C u

∃Inv(R).D)(c) [0,0.5]}. We want to check the

consistency of the knowledge base.

With Trans(R) and Inv(R), we have

Trans(Inv(R)). The fuzzy tableau is initialized

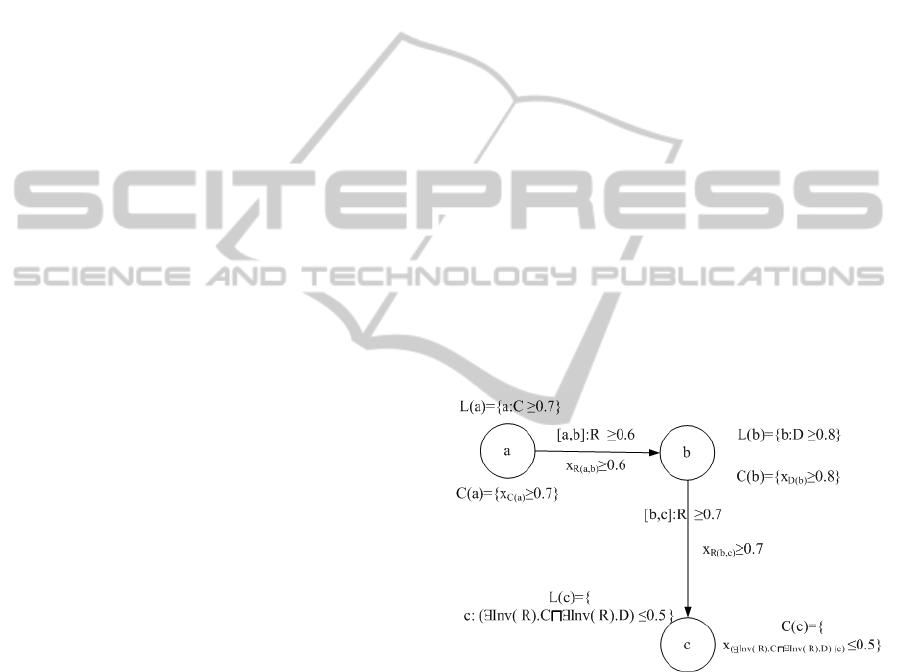
as shown in Figure 1.

Figure 1: The initial fuzzy tableau of example 3.

Next, since {c : (∃Inv(R).C u∃Inv(R).D) ≤ 0.5} ∈

L(c), the u

≤

-rule is triggered, the reasoning al-

gorithm adds {c : (∃Inv(R).C) ≤ x

} and {c :

(∃Inv(R).D) ≤ x

} to L(c), adds {x

(∃Inv(R).C)(c)

≤

(∃Inv(R).D)(c)

≤ x

+ x

= 1 + 0.5, x

≥ y,x

≥

1 − y,y ∈ {0,1},x

∈ [0, 1],x

∈ [0, 1]} to C (c).

Next, since {c : (∃Inv(R).C) ≤ x

} ∈ L(c), {c :

(∃Inv(R).D) ≤ x

} ∈ L(c), and we have [b,c] : R ≥

0.7, the ∃

≤

-rule is applicable, thus the reasoning al-

gorithm adds {b : C ≤ x

} and {b : D ≤ x

} to L(b),

adds {x

C(b)

≤ x

D(b)

≤ x

< 0.7,x

< 0.7} to

C (b). Note that the constraints x

< 0.7 and x

< 0.7

are added because of conjugation.

ICFC 2010 - International Conference on Fuzzy Computation

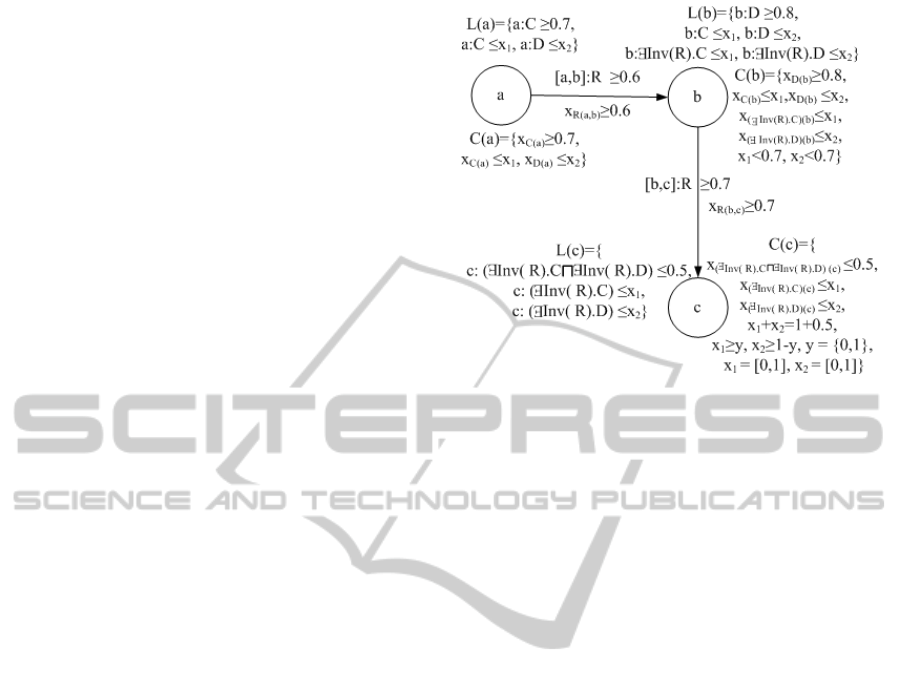
Next, since {c : (∃Inv(R).C) ≤ x

} ∈ L(c), {c :

(∃Inv(R).D) ≤ x

} ∈ L(c), we have [b,c] : R ≥

0.7 and Trans(Inv(R)), the ∃

≤,+

-rule is also ap-

plicable, thus the reasoning algorithm adds {b :

(∃Inv(R).C) ≤ x

} and {b : (∃Inv(R).D) ≤ x

} to

L(b), adds {x

(∃Inv(R).C)(b)

≤ x

(∃Inv(R).D)(b)

≤ x

} to

C (b).

Next, since {b : (∃Inv(R).C) ≤ x

} ∈ L(b), {b :

(∃Inv(R).D) ≤ x

} ∈ L(b), and we have [a,b] : R ≥

0.6, the ∃

≤

-rule is also applicable, thus the reason-

ing algorithm adds {a : C ≤ x

} and {a : D ≤ x

} to

L(a), adds {x

C(b)

≤ x

D(b)

≤ x

< 0.6,x

< 0.6}

to C (a).

Now the fuzzy tableau is shown in Figure 2.

Together with the default variable constraints, the

reasoning algorithm forms the following constraint

set:

subject to











C(a)

≥ 0.7,x

D(b)

≥ 0.8

R(a,b)

≥ 0.6,x

R(b,c)

≥ 0.7

(∃Inv(R).Cu∃Inv(R).D)(c)

≤ 0.5

(∃Inv(R).C)(c)

≤ x

(∃Inv(R).D)(c)

≤ x

+ x

= 1 + 0.5

≥ y,x

≥ 1 − y

C(b)

≤ x

D(b)

≤ x

< 0.7,x

< 0.7

C(a)

≤ x

D(a)

≤ x

< 0.6,x

< 0.6

(∃Inv(R).C)(b)

≤ x

(∃Inv(R).D)(b)

≤ x

C(a)

D(b)

R(a,b)

R(b,c)

∈ [0,1]

(∃Inv(R).Cu∃Inv(R).D)(c)

∈ [0,1]

(∃Inv(R).C)(c)

(∃Inv(R).D)(c)

∈ [0,1]

y ∈ {0, 1}

C(b)

D(b)

∈ [0,1]

(∃Inv(R).C)(b)

(∃Inv(R).D)(b)

∈ [0,1]

Using a Linear Programming solver, e.g., the

GLPK solver (GLPK, 2008), it is easy to show that

the constraint set is unsolvable. Therefore, the fuzzy

knowledge base is inconsistent.

Through this example, it is shown that the consis-

tency check of a knowledge base can be reduced to a

problem of constraints solving in linear programming.

The constraints solving can be processed either at the

end of the reasoning procedure when no further fuzzy

completion rules are applicable, or after each applica-

tion of a completion rule. The advantage of the later

case is that, in some situations, the computation effort

could be saved when the constraints solver can iden-

tify unsolvable constraints sets earlier in the reasoning

process. However, in other situations, since calling an

external solver is time consuming, frequent calls will

severely affect the overall performance. In the former

case, we only have to call the external solver once. In

Figure 2: The extended fuzzy tableau of example 3.

addition, we can apply some optimization strategies

such as trivial clash detection and individual groups

to improve the performance.

It is well known that there is always the trade-

off issue between the expressive power of a DL and

its computational complexity. The more expressive a

DL is, the higher its computational complexity. Hor-

rocks et. al presented an optimized version of the

tableau algorithm for classic SI in (Horrocks et al.,

1998), which generates completion trees whose depth

is polynomially bounded by the size of sub(A). It is

an interesting problem to investigate the applicability

of the optimization to the fuzzy case.

4 CONCLUSIONS

In this paper, we address the fuzzy instance entail-

ment problem with respect to a fuzzy knowledge base

and then present a fuzzy extension to the expressive

Description Logic SI based on Zadeh Logic and the

residual R-implication.

For real-world applications where a knowledge

base is considered as a means to store information

(both precise and imprecise) about individuals, usu-

ally more complex inferences other than consistency

checking are required. For example, users may want

to pose a query like “Given a knowledge base, what’s

the certainty of an assertion?”. Another kind of query

can be “How many individuals belong to a given con-

cept description with a conﬁdence greater than 0.5,

and what are they?” We describe the former query as

an instance range entailment problem and the later as

an f-retrieval problem. However, due to space limi-

tations, the reasoning methods for these problems are

REASONING WITH THE FUZZY DESCRIPTION LOGIC fZSI

omitted in this paper.

A prototype reasoner using SWI-Prolog and

GLPK has been under implementation based on the

ALC reasoner ALCAS (Spencer, 2006). It currently

supports functionalities to check consistency, fuzzy

instance entailment and f-retrieval of a fuzzy f

ALC

knowledge base. Part of our ongoing work considers

further development of the reasoner to support other

reasoning problems as well as more expressivity in

the fuzzy knowledge base.

As we pointed out in Section 2, the properties for

transitive roles and value restrictions also hold under

Product Logic. Therefore, another direction of future

work is to investigate the reasoning algorithms for ex-

pressive fuzzy Description Logics under norms from

other logics in the family of Fuzzy Logics.

REFERENCES

Baader, F., Calvanese, D., McGuinness, D. L., Nardi, D.,

and Patel-Schneider, P. F. (2003). The Description

Logic Handbook: Theory, Implementation and Ap-

plications. Cambridge University Press, Cambridge,

MA.

Berners-Lee, T., Hendler, J., and Lassila, O. (2001). The

semantic web. Scientiﬁc American, 284(5):34–44.

ıaz, S., De Baets, B., and Montes, S. (2010). General

results on the decomposition of transitive fuzzy re-

lations. Fuzzy Optimization and Decision Making,

9(1):1–29.

GLPK (2008). GNU linear programming kit. Technical

Report http://gnuwin32.sourceforge.net/packages/

glpk.htm.

Haase, P. and V

olker, J. (2005). Ontology learning and rea-

soning - dealing with uncertainty and inconsistency.

In Proceedings of Uncertainty Reasoning for the Se-

mantic Web, pages 45–55.

Horrocks, I. and Sattler, U. (1999). A description logic with

transitive and inverse roles and role hierarchies. J. of

Logic and Computation, 9(3):385–410.

Horrocks, I., Sattler, U., and Tobies, S. (1998). A PSPACE-

algorithm for deciding ALC I

-satisﬁability. LTCS-

Report 98-08, LuFg Theoretical Computer Science,

RWTH Aachen, Germany.

Horrocks, I., Sattler, U., and Tobies, S. (2000). Reasoning

with individuals for the description logic S H I Q . In

McAllester, D., editor, Proc. of the 17th Int. Conf. on

Automated Deduction (CADE 2000), volume 1831 of

Lecture Notes in Computer Science, pages 482–496.

Springer.

Jaeger, M. (1994). Probabilistic reasoning in terminological

logics. In Proc. of the 4th Int. Conf. on the Principles

of Knowledge Representation and Reasoning (KR94),

pages 305–316.

Koller, D., Levy, A., and Pfeffer, A. (1997). P-classic: A

tractable probabilistic description logic. In Proceed-

ings of the Fourteenth National Conference on Artiﬁ-

cial Intelligence (AAAI-97), pages 390–397.

Laskey, K. J., Laskey, K. B., Costa, P. C. G., Kokar,

M. M., Martin, T., and Lukasiewicz, T. (05 March,

2008). W3C incubator group report. Technical Re-

port http://www.w3.org/2005/Incubator/urw3, W3C.

Lee, H.-S. (2001). An optimal algorithm for computing the

maxmin transitive closure of a fuzzy similarity matrix.

Fuzzy Sets and Systems, 123(1):129–136.

Lukasiewicz, T. (2008). Fuzzy description logic programs

under the answer set semantics for the semantic web.

Fundamenta Informaticae, 82(3):289–310.

Martin-Recuerda, F. and Robertson, D. (2005). Discovery

and uncertainty in semantic web services. In Proceed-

ings of Uncertainty Reasoning for the Semantic Web,

page 188.

McGuinness, D. L. and van Harmelen, F. (2004).

Owl web ontology language overview.

http://www.w3.org/TR/owl-features/.

Mitsuishi, T. and Bancerek, G. (2003). Transitive closure of

fuzzy relations. Journal of Formalized Mathematics,

15.

Spencer, B. (2006). ALCAS: An ALC Reasoner for CAS.

http://www.cs.unb.ca/ bspencer/cs6795swt/alcas.prolog.

Stamou, G., van Ossenbruggen, J., Pan, J. Z., and Schreiber,

G. (2006). Multimedia annotations on the semantic

web. IEEE MultiMedia, 13:86–90.

Stevens, R., Aranguren, M. E., Wolstencroft, K., Sattlera,

U., Drummond, N., Horridge, M., and Rectora, A.

(2007). Using owl to model biological knowledge.

International Journal of Human-Computer Studies,

65(7):583–594.

Straccia, U. (2001). Reasoning within fuzzy description

logics. Journal of Artiﬁcial Intelligence Research,

14:137–166.

Yen, J. (1991). Generalizing term subsumption languages

to fuzzy logic. In Proc. of the 12th Int. Joint Conf. on

Artiﬁcial Intelligence (IJCAI’91), pages 472–477.

Zadeh, L. A. (1965). Fuzzy sets. Information and Control,

8(3):338–353.

Zhao, J. (2010). Uncertainty and Rule Extensions to De-

scription Logics and Semantic Web Ontologies, chap-

ter 1, pages 1–22. Advances in Semantic Computing.

Technomathematics Research Foundation. accepted.

Zhao, J. and Boley, H. (2010). Knowledge Representa-

tion and Reasoning in Norm-Parameterized Fuzzy De-

scription Logics. Canadian Semantic Web: Technolo-

gies and Applications. Springer.

ICFC 2010 - International Conference on Fuzzy Computation