SVM-BASED HUMAN DETECTION COMBINING SELF-QUOTIENT
ε-FILTER AND HISTOGRAMS OF ORIENTED GRADIENTS
Mitsuharu Matsumoto
The University of Electro-Communications, 1-5-1, Chofugaoka, Chofu-shi, Tokyo, 182-8585, Japan
Keywords:
Human detection, Self-quotient ε-filter, Histograms of oriented gradients, Feature extraction, Noise corrupted
image.
Abstract:
This paper describes a noise robust SVM-based human detection combining self-quotient ε-filter (SQEF) and
histograms of oriented gradients (HOG). Although human detection combining HOG and SVM is a powerful
approach, as it uses local intensity gradients, it is difficult to handle noise corrupted images. To handle noise
corrupted images, we introduce self-quotient ε-filter (SQEF), and implement it in human detection combining
HOG and SVM. SQEF is an advanced self-quotient filter (SQF), and can clearly extract features from the
images not only when they have illumination variations but also when they are corrupted with noise. The new
approach gives a robust human detection from noise corrupted images using the data trained by intact images
without noise.
1 INTRODUCTION
Detecting human from images is a challenging task
in owing to their variable appearance and the wide
range of poses that they can adopt. The important re-
quirement is to extract the feature from the images
clearly, even in backgrounds under different illumina-
tion. Histogram of Oriented Gradients (HOG) algo-
rithm is a useful approach to match this requirement
(Dalal and Triggs, 2005). It can extract the feature
clearly compared to other existing feature sets includ-
ing wavelets (Mohan et al., 2001; Viola et al., 2003).
The approach is related to edge orientation (Freeman
and Roth, 1995; Freeman et al., 1996), SIFT descrip-
tors (Lowe, 2004) and shape contexts (Belongie et al.,
2001). Although locally normalized HOG detectors
are attractive approaches to detect the human from
the image, it is difficult to detect them from the noise
corrupted images because it uses local intensity gra-
dients.
To handle the problems, this paper introduces self-
quotient ε-filter (SQEF), which is an advanced noise
robust self-quotient filter (SQF) and propose a noise
robust SVM-based human detection combiningSQEF
and HOG. Self-quotient filter (SQF) is a simple non-
linear filter and can extract the feature from an image
with light variation (Wang et al., 2004a; Wang et al.,
2004b). It needs only an image, and can extract in-
trinsic lighting invariant property of an image, while
removing extrinsic factor corresponding to the light-
ing. Feature extraction using SQF is simpler than that
using multi-scale smoothing (Gooch et al., 2004). It
can extract the outline of the objects independent of
shadow region. However, it is difficult to extract the
shape and texture when the noise damages the im-
age as SQF assumes that the image does not include
noise. The noise influence becomes large due to the
self-quotient effect of SQF.
Self-quotient ε-filter (SQEF) (Matsumoto, 2010)
is a nonlinear filter combining the idea of SQF and
ε-filter (Arakawa and Okada, 2005). Although many
studies have been reported to reduce the small ampli-
tude noise while preserving the edge (Himayat and
Kassam, 1993; Tomasi and Manduchi, 1998), it is
considered that ε-filter is a promising approach due
to its simple design. It does not need to have the sig-
nal and noise models in advance. It is easy to be de-
signed and the calculation cost is small because it re-
quires only switching and linear operation. We can
clearly extract the feature from noise corrupted im-
age images by defining SQEF as the ratio of two dif-
ferent ε-filters. In this paper, we aim to reduce the
noise influence by employing SQEF as preprocessing
of HOG.
This paper is organized as follows. In section
2, we briefy introduce SQEF, and discuss the mer-
its of SQEF compared to SQF. We also describe the
algorithm of SVM-based human detection combining
241
Matsumoto M..
SVM-BASED HUMAN DETECTION COMBINING SELF-QUOTIENT -FILTER AND HISTOGRAMS OF ORIENTED GRADIENTS.
DOI: 10.5220/0003055002410245
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
241-245
ISBN: 978-989-8425-32-4
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

Input
image
Normalized
Gamma and Color
Self quotient
ε
-filter
Compute
gradients
SVM
Person /
Non-person
Classification
Weighted vote into
space & orientation
cells
Contrast normalized
over detection
window
Collect HOG's
over detection
window
Figure 1: An overview of our feature extraction and object
detect chain.
SQEF and HOG. Experimental results are shown to
clarify the effectiveness of the proposed method for
human detection from noise corrupted images com-
pared to other approaches in section 3. A libsvm
(Chang and Lin, 2001), MIT pedestrian test set (Oren
et al., 1997; Papageorgiou et al., 1998; Mohan et al.,
2001; Papageorgiou and Poggio, 2000) and standard
image database (SIDBA) are used as a SVM classifier,
positive sample images and negative sample images,
respectively throughout the experiments. Conclusion
is given in section 4.
2 PROPOSED ALGORITHM
In this section, we describe the proposed algorithm.
Figure 1 shows the procedure of our approaches. In
the proposed method, we first extract the feature from
the noise corrupted image by using self-quotient ε-
filter (SQEF) to eliminate not only illumination vari-
ations but also noise influence. Some examples are
shown to clarify the difference between self-quotient
filter (SQF) (Wang et al., 2004a; Wang et al., 2004b)
and SQEF. Figure 2 shows the examples of filter out-
put of SQEF to show its robustfeature extraction from
noise corrupted images. We also show the filter output
of self-quotient filter (SQF). Fig.2(a) shows a sam-
ple image from MIT pedestrian database (Oren et al.,
1997; Papageorgiou et al., 1998; Mohan et al., 2001;
Papageorgiou and Poggio, 2000). Figs.2(b) and 2(c)
show the filter outputs of SQF and SQEF, respectively
when we used the original image. On the other hand,
Fig.2(d) shows the sample image corrupted with 40%
impulse noise. Figs.2(e) and 2(f) show the filter out-
puts of SQF and SQEF, respectively when we used the
impulse noise corrupted image. As shown in Fig.2,
both SQF and SQEF can extract the feature from the
original image. However, SQF cannot extract its fea-
ture from the impulse noise corrupted image, while
SQEF can extract the feature from the impulse noise
corrupted image.
Let x(i
1
, i
2
) be the image intensity at the point i =
(i
1
, i
2
) in the image. The aim of SQF is to separate
the intrinsic property and the extrinsic factor, and to
remove the extrinsic factor. To handle the problem,
SQF assumes that a smoothed version of an image has
approximately the same illumination as the original
(a) A sample image
from MIT pedestrian
database (file name:
per00008.pgm)
(b) Filter output of
SQF when we used
original image
(c) Filter output of
SQEF when we used
original image
(d) Impulse noise
corrupted image (40%
impulse noise)
(e) Filter output
of SQF when we
used impulse noise
corrupted image
(f) Filter output
of SQEF when we
used impulse noise
corrupted image
Figure 2: Self-quotient image and self-quotient ε-filter from
original image and impulse noise corrupted image
one. In SQF, we first calculate the following equation:
y(i
1
, i
2
) =
x(i
1
, i
2
)
F[x(i
1
, i
2
)]
, (1)
where x(i
1
, i
2
) is the original image and F is the
smoothing function. Due to the process of Eq.1, the
texture and edge can be extracted because the origi-
nal image is divided by the smoothed image. How-
ever, SQF assumes that the image does not include
the noise. When we consider the noise corrupted
image, the noise is reduced in the smoothed images
F[x(i
1
, i
2
)], while the original image x(i
1
, i
2
) includes
the noise. As a result, the influence from the noise in
SQF is emphasized very much as shown in Fig.2 due
to the self-quotient effect of SQF in Eq.1.
A simple idea to solve the noise influence in SQF
is to use two smoothed filters instead of original im-
age as follows:
y(i
1
, i
2
) =
F
1
[x(i
1
, i
2
)]
F
2
[x(i
1
, i
2
)]
. (2)
F
1
and F
2
should be different because the output al-
ways becomes 1 if F
1
and F
2
are the same smoothed
ICFC 2010 - International Conference on Fuzzy Computation
242

filter.
However, even if we design SQF by using two dif-
ferent smoothed filters, not only the noise is smoothed
but also the texture and shape are blurred. As the blur
level of one smoothed filter is different from the other,
it is also difficult to handle impulsive noise. Hence,
we need to employ alternative filters, which can re-
duce the small amplitude noise effectively, while pre-
serving the texture and shape information instead of
simple smoothed filter. The alternative filters should
be simple to keep the simplicity of SQF.
Based on the aboveprospects, self-quotientε-filter
(SQEF) is designed as follows:
y(i
1
, i
2
) =
Φ
ε
1
[x(i
1
, i
2
)]
Φ
ε
2
[x(i
1
, i
2
)]
, (3)
where Φ
ε
represents ε-filter described as follows:
z(i
1
, i
2
) =
Φ
ε
[x(i
1
, i
2
)] = x(i
1
, i
2
) + (4)
K
∑
j
1
=−K
K
∑
j
2
=−K
a( j
1
, j
2
)F(x(i
1
+ j
1
, i
2
+ j
2
) − x(i
1
, i
2
)),
where a( j
1
, j
2
) represents the filter coefficient.
a( j
1
, j
2
) is usually constrained as follows:
K
∑
j
1
=−K
K
∑
j
2
=−K
a( j
1
, j
2
) = 1. (5)
F(x) is the nonlinear function described as follows:
|F(x)| ≤ ε : −∞ ≤ x ≤ ∞, (6)
where ε is a constant number constrained as follows.
0 ≤ ε. (7)
It should be noted that calculation cost of ε-filter is
small because it requires only switching and linear
operation. See the references (Arakawa and Okada,
2005) if the reader would like to know the details
about ε-filter.
When we apply SQEF to impulse noise corrupted
image, it is considered that both ε-filters in SQEF
keep the impulse noise in the image unlike when two
smoothed filters are employed. Hence, when one fil-
ter output in SQEF is divided by the other filter in
SQEF, the impulse noise effect is reduced by the self-
quotient effects.
We next apply HOG procedure to SQEF output.
Figure 3 shows the procedure of HOG from SQEF
outputs. The method is based on evaluating well-
normalized local histograms of image gradient orien-
tations in a dense grid. As local object appearance and
shape are kept in SQEF output, the gradient intensity
and the gradient direction of SQEF are calculated for
all the pixels as follows:
f
i
1
(i
1
, i
2
) = y(i
1
+ 1, i
2
) − y(i
1
− 1, i
2
) (8)
⋅⋅⋅
FrequencyGradient calculation
Filter output of SQEF
⋅⋅⋅
Frequency
Feature vector
Cell
sliding
Connection Voting
Figure 3: Procedure of Histogram of Oriented Gradients
(HOG) from SQEF output.
f
i
2
(i
1
, i
2
) = y(i
1
, i
2
+ 1) − y(i
1
, i
2
− 1) (9)
m(i
1
, i
2
) =
q
f
2
i
1
+ f
2
i
2
(10)
θ(i
1
, i
2
) = arctan
f
i
2
f
i
1
(11)
The basic idea of HOG is that local object ap-
pearance and shape can often be characterized rather
well by the distribution of local intensity gradients or
edge directions, even without precise knowledge of
the corresponding gradient or edge positions (Dalal
and Triggs, 2005). In practice, this is implemented
by dividing the filter output into small spatial re-
gions (“cells”), for each cell accumulating a local 1-
D histogram of gradient directions or edge orienta-
tions over the pixels of cell. The obtained direction
θ (0
◦
≤ θ ≤ 180
◦
) is divided with 20
◦
intervals. 9
dimensional feature vector is generated by adding the
gradient intensity m(i
1
, i
2
). We then regard 3 × 3 cells
as “Block” and generate many blocks by sliding on a
pixel to pixel basis. The feature vector is finally ob-
tained by combining all the feature vector. The ob-
tained feature vector is adopted to SVM.
3 EXPERIMENTS
We conducted the recognition experiments using im-
pulse noise corrupted images to show the effective-
ness of the proposed method.
MIT pedestrian database and SIDBA were em-
ployed as image database. MIT pedestrian database
contains 900 images. The size is 64 pixel × 128 pixel.
Some non person images were selected from standard
image database (SIDBA). 900 64 pixel × 128 pixel
SVM-BASED HUMAN DETECTION COMBINING SELF-QUOTIENT W-FILTER AND HISTOGRAMS OF
ORIENTED GRADIENTS
243

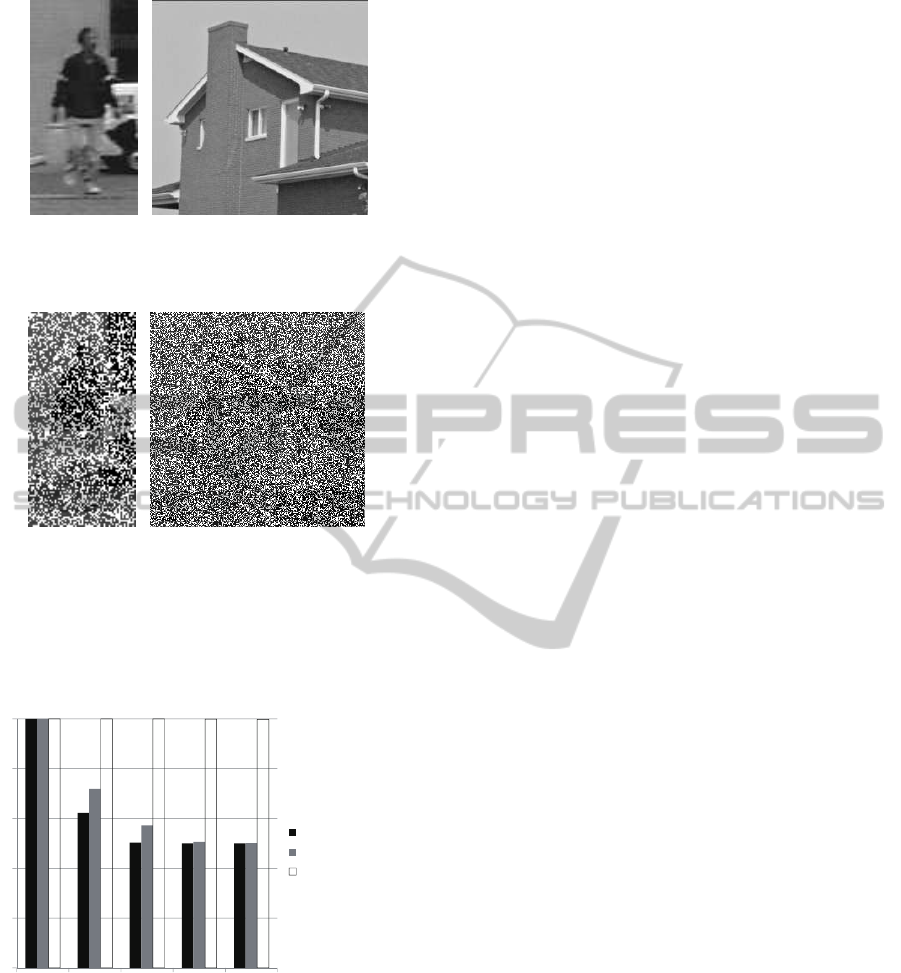
(a) Person im-
age from MIT
pedestrian database
(per00001.pgm)
(b) Non-person image from SIDBA
(Airplane)
(c) Person image
from MIT pedestrian
database with 40%
impulse image
(per00001.pgm)
(d) non-person image from SIDBA
with 40% impulse noise (Airplane)
Figure 4: Sample images of person image and non-person
image (Original and noise corrupted images).
0
0.2
0.4
0.6
0.8
1
0% 10% 20% 30% 40%
Original image
Self-quotient filter
Self-quotient ε-filter
Figure 5: Experimental results of human detection from im-
pulse noise corrupted image.
images were cut from them. We also prepared im-
pulsive noise corrupted images by adding the impulse
noise to the above 1800 images. Noise percentage
changed from 10% to 40% with 10% intervals. Figure
4 shows original person / non-person images and its
noise-corrupted version. Our aim is to detect human
from these types of noise corrupted images not by us-
ing the data trained by the impulse noise corrupted
image but by using the data trained by intact images
without noise. As a SVM tool, we used libsvm, a
library for support vector machines (Chang and Lin,
2001), and employed default setting and parameters
throughout the experiments for simplicity.
In the experiments, we used original 450 pedes-
trian images from MIT pedestrian database and 450
non-person images from SIDBA. We tried to clas-
sify the impulse noise corrupted image by using the
training data. The test images are the remaining 450
pedestrian images from MIT pedestrian database and
the remaining 450 non-person images from SIDBA
with impulse noise, which are different from the train-
ing images. For comparison, we also tested to classify
them using the method combining HOG and SVM,
and the method combining SQF, HOG and SVM. Fig-
ure 5 shows the recognition results. As shown in
Fig.5, it was difficult to classify the images using the
method combining HOG and SVM when the image
was corrupted with the impulse noise. The results
were still bad even when we used the method com-
bining SQF, HOG and SVM. On the other hand, the
proposed approach could detect human from noise
corrupted images over 90% using training data with
intact images without noise.
4 CONCLUSIONS
This paper proposed a noise robust SVM-based hu-
man detection combining self-quotient ε-filter and
histogram of oriented gradients. We compared the re-
sults of our approach to the results of HOG and SVM,
and the results of SQF, HOG and SVM. Throughout
the experiments, the proposed method could robustly
detect pedestrians from noise corrupted images using
the training data with the clean image without noise,
while it is difficult to detect pedestrians using other
approaches. Future works include the applications of
our method to robot vision. Detailed study of effects
of the parameters should also be required. We also
would like to apply the proposed method to medical
images to detect disease site from noise corrupted im-
ages.
ACKNOWLEDGEMENTS
This research was supported by the research grant
of Support Center for Advanced Telecommunications
Technology Research (SCAT), by the research grant
of Foundation for the Fusion of Science and Tech-
nology, by Special Coordination Funds for Promoting
ICFC 2010 - International Conference on Fuzzy Computation
244

Science and Technology, and by the Ministry of Edu-
cation, Science, Sports and Culture, Grant-in-Aid for
Young Scientists (B), 20700168, 2008.
REFERENCES
Arakawa, K. and Okada, T. (2005). ε-separating nonlinear
filter bank and its application to face image beautifica-
tion. In IEICE Transactions on Fundamentals, pages
1216–1225. IEICE.
Belongie, S., Malik, J., and Puzicha, J. (2001). Matching
shapes. In Proc. of Int’l Conf. on Computer Vision,
pages 454–461. IEEE.
Chang, C.-C. and Lin, C.-J. (2001). LIBSVM:
a library for support vector machines. In
http://www.csie.ntu.edu.tw/ cjlin/libsvm.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In Proc. of Int’l Conf.
on Computer Vision and Pattern Recognition., pages
886–893. IEEE.
Freeman, W. T. and Roth, M. (1995). Orientation his-
tograms for hand gesture recognition. In Proc. of Int’l
Workshop on Automatic Face and Gesture Recogni-
tion, pages 296–301. IEEE.
Freeman, W. T., Tanaka, K., Ohta, J., and Kyuma, K.
(1996). Computer vision for computer games. In
Proc. of Int’l Conf. on Automatic Face and Gesture
Recognition, pages 100–105. IEEE.
Gooch, B., Reinhard, E., and Gooch, A. (2004). Human fa-
cial illustrations: Creations and psychological evalua-
tion. In ACM transactions on Graphics, pages 27–44.
ACM.
Himayat, N. and Kassam, S. (1993). Approximate per-
formance analysis of edge preserving filters. In
IEEE Trans. on Signal Processing., pages 2764–2777.
IEEE.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. In Int’l Journal of Computer Vi-
sion, volume 60, pages 91–110. Springer.
Matsumoto, M. (2010). Feature extraction from noisy face
image using self-quotient ε-filter. Proc. of Int’l Conf.
on Computer Engineering and Technology, pages
395–399.
Mohan, A., Papageorgiou, C., and Poggio, T. (2001).
Example-based object detection in images by compo-
nents. In IEEE Trans. on PAMI., volume 23, pages
349–361. IEEE.
Oren, M., Papageorgiou, C., Sinha, P., Osuna, E., and Pog-
gio, T. (1997). Pedestrian detection using wavelet
templates. In Proc. of IEEE Conf. on Computer Vi-
sion and Pattern Recognition, pages 193–199. IEEE.
Papageorgiou, C., Oren, M., and Poggio, T. (1998). A gen-
eral framework for object detection. In Proc. of Int’l
Conf. on Computer Vision, pages 555–562. IEEE.
Papageorgiou, C. and Poggio, T. (2000). A trainable sys-
tem for object detection. In Int’l Journal of Computer
Vision, volume 38, pages 15–33. Springer.
Tomasi, C. and Manduchi, R. (1998). Bilateral filtering for
gray and color images. In Proc. of Int’l Conf. on Com-
puter Vision. IEEE.
Viola, P., Jones, M. J., and Snow, D. (2003). Detecting
pedestrians using patterns of motion and appearance.
In Proc. of Int’l Conf. on Computer Vision, volume 1,
pages 734–741. IEEE.
Wang, H., Li., S. Z., and Wang, Y. (2004a). Face recogni-
tion under varying lighting conditions using self quo-
tient image. In Proc. of Int’l Conf. on Automation Face
and Gesture Recognition. IEEE.
Wang, H., Zhang, J. J., Li., S. Z., and Wang, Y. (2004b).
Shape and texture preserved non-photorealistic ren-
dering. In Computer animation and virtual worlds,
pages 453–461. John Wiley and Sons, Ltd.
SVM-BASED HUMAN DETECTION COMBINING SELF-QUOTIENT W-FILTER AND HISTOGRAMS OF
ORIENTED GRADIENTS
245