
FAULT DIAGNOSIS IN ROTATING MACHINERY
USING FUZZY MEASURES AND FUZZY INTEGRALS
Masahiro Tsunoyama, Kensuke Masumori
Niigata Institute of Technology, 1719 Fujihashi, Kashiwazaki, Niigata 945-1195, Japan
Hayato Hori, Hirokazu Jinno, Masayuki Ogawa, Tatsuo Sato
Niigata-Worthington Co., Ltd. 1-32 Shinbashi, Kashiwazaki, Niigata 945-0056, Japan
Keywords: Fault diagnosis, Fuzzy measure, Fuzzy integral, Vibration diagnosis.
Abstract: In the fault diagnosis of rotating machinery using fuzzy measures and fuzzy integrals, the optimization of
membership functions and identification of fuzzy measures are important for accurate diagnosis. Herein, a
method for optimizing membership functions is proposed based on the statistical properties of vibration
spectra and identifying fuzzy measures based on interaction levels using partial correlation coefficients
between spectra. The possibility of a given fault is obtained from fuzzy integrals using membership degrees
determined by the membership function, and the fuzzy measures for the set of spectra. The method is also
evaluated using the example of diagnosis of misalignment and unbalance faults.
1 INTRODUCTION
Due to the widespread use of rotating machinery and
the growing demand for reliability and cost
efficiency, condition based maintenance (CBM) is
being more widely used in many industries. CBM
has proved effective in accurately diagnosing faulty
machinery. Vibration based diagnosis is often used
in CBM because it requires less expensive
equipment, can diagnose a variety of faults, and
vibration data may easily be obtained. However, the
technique requires highly skilled engineers to make
an accurate diagnosis.
Several diagnostic techniques have been
proposed (Liu 2007) for automatic diagnosis or to
aid diagnostic engineers. Some of the techniques use
fuzzy measures and fuzzy integrals to encompass the
existing knowledge of skilled engineers (Tsunoyama
2008). However, constructing a membership
function and identifying fuzzy measures is difficult
and time consuming.
A method for diagnosis of rotating machinery
based on fuzzy measures and fuzzy integrals is
proposed herein. In this method, first the
membership function is optimized using the
statistical properties of the vibration spectra. Then
fuzzy measures are identified using the partial
correlation coefficients of the spectra and
importance factors identified by skilled engineers.
The possibility of a fault existing in the machinery is
determined by fuzzy integrals using the membership
degrees of the vibration spectra and fuzzy measures.
2 VIBRATION SPECTRA AND
MEMBERSHIP FUNCTION
2.1 Faults in Rotating Machinery and
Associated Vibration Spectra
Several kinds of faults occur in rotating machinery
including abnormal vibration and fluid leaks. As a
large number of these faults are accompanied by
vibration, the method proposed herein focuses on the
diagnosis of such faults through analysis of the
associated vibrations.
Vibration diagnosis uses membership degrees for
spectra determined from the root-mean-square
(RMS) values. However, the RMS values of spectra
associated with a fault may vary depending on the
position of the fault or the degree of damage. Herein,
the normal probability distribution for the RMS
values of spectra is based on the statistical properties.
120
Tsunoyama M., Masumori K., Hori H., Jinno H., Ogawa M. and Sato T..
FAULT DIAGNOSIS IN ROTATING MACHINERY USING FUZZY MEASURES AND FUZZY INTEGRALS .
DOI: 10.5220/0003056001200124
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICFC-2010), pages
120-124
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)
The parameters,
and
are average and standard
deviation of the normal probability distribution,
respectively.
2.2 Membership Function and its
Optimization
Several types of membership functions exist such as
triangular, exponential, and trapezoidal. Herein, the
trapezoidal type is used.
In fault diagnosis, diagnosed results are
classified into four cases, shown in Table 1.
Table 1: Diagnoses.
Case Cause of fault Diagnosed result
1Not Fα
2F
α
3Fα
4
Not F
α
F
α
F
β
When
F
is diagnosed, Cases 2 and 4 are correct but
Cases 1 and 3 are not. Moreover, Cases 1 and 2 are
exclusive, and Cases 3 and 4 are also exclusive.
Therefore, the membership function is optimized by
maximizing the mean value of the membership
degree for Case 2 and minimizing that for Case 3.
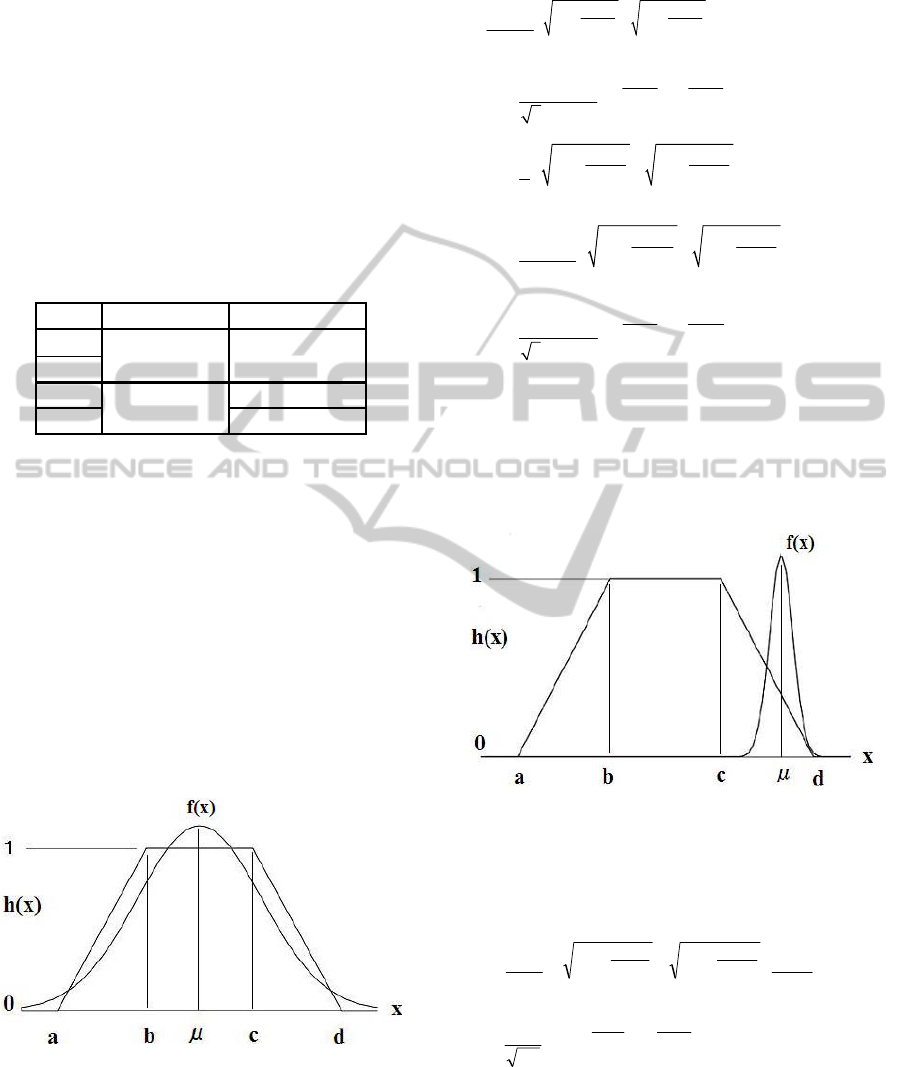
Figure 1 shows the membership function and normal
distribution for
F
for Case 2. In the figure, h(x) is
the trapezoidal membership function and f(x) is the
normal probability distribution for
F
. The optimum
values of the parameters are obtained by solving Eq.
(1). These equations are obtained by the integral of
the normal distribution and the membership function.
Figure 1: Membership function and probability
distribution for Case 2.
22
22
22
11
2
dbcd
aabc
ab
hxdFx hxdFx hxdFx hxdFx
a
ee
ba
22
22
22
22
22
22
22
22
22
22
22
22
2
1
11
2
11
2
2
ab
bc
dc
cd
ee
ba
ee
d
ee
dc
ee
dc
(1)
Subsequently, the mean value of the membership
degree is minimized for Case 3. Figure 2 shows the
membership function and the normal probability
distribution for
F
for Case 3 when
of the normal
distribution for
F
is larger than the average of
F
.
Figure 2: Membership function and probability
distribution for Case 3.
The mean value of the membership degree is:
2
2
2
2
22
22
22
2
2
2
11
1
dc
dc
d
c
ee
d
ee
cd
xdFxhxdFxh
(2)
Conversely, when
of
F
is less than the average of
F
, the mean value of the membership degree is:
FAULT DIAGNOSIS IN ROTATING MACHINERY USING FUZZY MEASURES AND FUZZY INTEGRALS
121

22
2
2
2
2
22
22
11
2
2
2
1
ba
da
b
a
ee
a
ee
ab
xdFxhxdFxh
(3)
3 FUZZY MEASURE AND FUZZY
INTEGRAL
3.1 Fuzzy Measure for the Spectra and
the Fuzzy Integral
A fuzzy measure
g
is a set function on X satisfying
the following conditions:
,0)(],1,0[2:
gg
X
(4)
)()( BgAgXBA
},,,{
21 n
sssX
The fuzzy measure can cope with the following
three interactions between the sets A and B.
(1) No interaction between A and B.
(2) Positive synergy between A and B.
(3) Negative synergy between A and B.
Several fuzzy integrals have been proposed such as
Sugeno’s and Choquet integrals(Grabisch 2000). In
this paper, the Choquet integral is used. The
Choquet integral of a non-negative function h on
},,,{
21 n
sssX
with respect to
g
is defined:
).()]()([)()(
1
1 i
X
n
i
ii
AgshshdgshC
(5)
},,,{
1 niii
sssA
In the definition, it may be assumed, without loss of
generality, that
12
() () ().
n
hs hs hs£ £⋅⋅⋅ £
3.2 Identification of the Fuzzy Measure
3.2.1 Fuzzy Measure based on Interaction
Level
Several methods for fuzzy measure identification
have been proposed (Wang 1992). However, they
are difficult to apply fault diagnosis of rotating
machinery, since several parameters must be
assigned experimentally before identification. In this
paper, the fuzzy measure based on interaction
level(Taya 2006) is used and is defined:
0 , 0 , 0
0
0
np
AnApA
Ag
(6)
jiij
ji
Iji
k
A
Ii
iA
wwkw
A
ijA
,
,
0
min ,
jiij
ji
Iji
k
A
wwk
A
ij
,
,
0
min
AsiI
iA
|
n
wwwW ,,,
21
1
1
n
i
i
w
where:
np
,,
0
are the coefficients for interaction;
)1( niw
i
are importance factors of the spectra,
as identified by skilled engineers; coefficient
ji
k
,
is a
partial correlation coefficient between
i
s and
j
s excluding the effects of other spectra (Sipley
2000).
3.2.2 Determining
np
,,
0
Let
)1( nish
i
satisfy
i
shsh
1
n
sh
. Then the fuzzy measure must satisfy the
conditions:
11 ,
1
1
1
niAgAg
Ag
ii
npo
(7)
where:
.,,
1
nii
ssA
XA
We can obtain
np
,,
0
by maximizing
Z
in Eq.
(8) under the conditions in Eq.(7) using linear
programming such as the Simplex method.
np
Z
(8)
4 EXAMPLE DIAGNOSIS
In this example, we evaluate the proposed method
by looking at the possibility of a Case 2 or Case 3
fault (Table 1). Here, fault
F
is misalignment and
ICFC 2010 - International Conference on Fuzzy Computation
122

F
is imbalance. The spectra used for fault diagnosis
of misalignment are 1N, 2N, and 3MN where 1N,
2N, and 3MN are the fundamental frequency, second
harmonic, and third harmonic and over, respectively.
The importance factors given by skilled engineers
for the spectra are:
1.0,6.0,3.0
321
MNNN
www
The RMS values and membership degrees obtained
from the optimized membership function are shown
in Table 2.
Table 2: RMS value and membership degree for
misalignment and unbalance.
Misalign-
ment
Unbalance
1N 0.457 0.911
2N 0.457 0.019
3MN 0.037 0.013
1N 0.8 0.6
2N 1.0 0.2
3MN 0.7 0.3
RMS value
Membership
degree
The partial correlation coefficients of vibration
spectra obtained from field data are:
24.0,41.0,73.0
3,13,22,1
MNNMNNNN
kkk
4.1 Fuzzy Measure
The conditions for a fuzzy measure for misalignment
are:
NNNpNN
wkwwAgAg
12,121021
)()(,1)(
N
wAg
103
)(
)()()(
321
AgAgAg
Maximizing Eq. (8) under the above conditions, we
obtain:
.0,78.0
0
np
The fuzzy measures are composed for the above
value and the importance factors for the spectra. The
fuzzy measures for misalignment are:
87.0)()(
,1)(
12,12102
1
NNNpNN
wkwwAg
Ag
23.0)(
103
N
wAg
The fuzzy measures for imbalance are:
33.0)()(
,1)(
33,1310
'
2
1
MNMNNpMNN
wkwwAg
Ag
24.0)(
10
'
3
N
wAg
4.2 Fuzzy Integral
The fuzzy integral for misalignment is obtained
using the fuzzy measures and membership degree
using the following equation:
88.0)())1()2((
)())3()1(()()3(
)()]()([)()(
3
21
1
1
AgNhNh
AgMNhNhAgMNh
AgshshdgshC
i
X
n
i
ii
The fuzzy integral for imbalance is obtained in the
same manner:
30.0)())3()1((
)())2()3(()()2(
)()]()([)()(
'
3
'
21
1
1
AgMNhNh
AgNhMNhAgNh
AgshshdgshC
i
X
n
i
ii
From the above fuzzy integrals, the possibility of
misalignment (Case 2 in Table 1) was determined as
0.88 and the possibility of imbalance (Case3 in
Table 1) was determined as 0.3.
5 CONCLUSIONS
Herein, a method for diagnosing faults in rotating
machinery using fuzzy measures and fuzzy integrals
is proposed. The membership function giving the
membership degree of the spectra is optimized based
on the statistical properties. The fuzzy measures are
based on the interaction level using the importance
factor of the spectra and partial correlation
coefficients between spectra.
The results of the evaluation show that
misalignment (correct result) is about three times
more probable than imbalance (wrong result). In
future work, the authors will apply this method to
other fault diagnoses and evaluate the method using
extensive field data.
REFERENCES
Liu, X., Ma, L. and Mathew, J., 2007. Rotating machinery
fault diagnosis on fuzzy data fusion techniques, 2nd
World Congress on Engineering Asset Management
and the 4th International Conference on Condition
Monitoring, pp. 1309-1318, Harrogate England.
Tsunoyama, M., Jinno, H., Ogawa M. and Sato, T., 2008.
An Application of Fuzzy Measure and Integral for
Diagnosing Faults in Rotating Machines, Tools and
Applications with Artificial Intelligence, pp. 121-133,
Springer Berlin.
FAULT DIAGNOSIS IN ROTATING MACHINERY USING FUZZY MEASURES AND FUZZY INTEGRALS
123

Taya, M. and Murofushi, T., 2006. Fuzzy measure
identification for bootstrapped Choquet integral model
in multicriteria decision making. International
Conference on Soft Computing and Intelligent Systems
and International Symposium on advanced Intelligent
Systems 2006, pp.1402-1407, Tokyo, Japan.
Sipley, B., 2000. Cause and correlation in Biology.
Cambridge University Press.
Grabisch, M., Murofushi, T. and Sugeno, M., 2000. Fuzzy
Measures and Integrals: Theory and Applications,
Springer.
Wang, Z. and Klir, G. J., 1992. Fuzzy Measure Theory,
Plenum Press.
ICFC 2010 - International Conference on Fuzzy Computation
124
