
ACO FOR OPTIMAL SENSOR LAYOUT
Stefka Fidanova
1
, Pencho Marinov
1
and Enrique Alba
2
1
Institute for Parallel Processing, Bulgarian Academy of Science, Acad. G. Bonchev str. bl.25A, 1113 Sofia, Bulgaria
2
E.T.S.I. Informatica, Grupo GISUM (NEO), University of Malaga, Malaga, Spain
Keywords:
ACO, Wireless sensor networks.
Abstract:
Metaheuristic methods have frequently been applied to telecommunication problems in the last years. One of
these problems is Wireless Sensor Network (WSN) layout, which is an NP-hard optimization problem. The
sensors sent their sensing results to a special station called the High Energy Communication Node (HECN).
The sensing area of the WSN is the union of the individual sensing areas of the nodes. When deploying
a WSN, the major objective is to achieve full coverage of the terrain (sensor field). Another objectives are
also to use a minimum number of sensor nodes and to keep the connectivity of the network. In this paper
we address a WSN layout problem in which full coverage and connectivity are treated as constraints, while
objective function is the number of the sensors. To solve it we propose Ant Colony Optimization (ACO)
algorithm. The terrain is modeled with 500 × 500 points grid and both sensing radius and communication
radius are set to 30. We compare our results with existing evolutionary algorithms.
1 INTRODUCTION
Telecommunications are an important symbol of our
present information society. Telecommunication is a
field in which many open research lines are challeng-
ing the research community. Nowadays, the trend in
telecommunication networks is having highly decen-
tralized, multi-node networks. From small, geograph-
ically close, size-limited local area networks the evo-
lution has led to the huge worldwide Internet. This
same path is followed by wireless communications,
where we can already see wireless telephony reach-
ing virtually any city in the world. In this context
WSN have recently become a hot topic in research.
A WSN allows an administrator to automatically and
remotely monitor almost any phenomenon with a pre-
cision unseen to the date. The use of multiple small
cooperative devices yields a brand new horizon of
possibilities yet offers a great amount of new prob-
lems to be solved. WSN have so far been employed
in military activities such es reconnaissance, surveil-
lance, and target acquisition (Deb et al., 2000), en-
vironmental activities such as forest fire prevention,
geophysical activities such as volcano eruptions study
(Werner-Allen et al., 2006), biomedical purposes such
as health data monitoring (Yuce et al., 2007) or civil
engineering (Paek et al., 2004).
When deploying a WSN, the positioning of the
sensor nodes becomes one of the major concerns. The
coverage obtained with the network and the economic
cost of the network depend directly of it. Since many
WSN can have large numbers of nodes, the task of
selecting the geographical positions of the nodes for
an optimally designed network can be very complex.
Therefore, metaheuristics seem an interesting option
to solve this problem.
In this paper we propose a solution method for
the WSN layout problem using ACO. We focus on
minimizing the number of nodes, while the full cov-
erage of the network and connectivity are considered
as constraints.
Jourdan (Jourdan, 2000) solved an instance of
WSN layout using a multiobjectivegenetic algorithm.
In there formulation a fixed number of sensors had
to be placed in order to maximize the coverage. In
(Molina et al., 2008) are proposed several evolution-
ary algorithms to solve the problem.
For solving the WSN layout problem, the cover-
age has to satisfied some restrictions and the biggest
possible coverage will be preferred: the number of
sensor nodes should be kept low for economical rea-
sons and the network needs to be connected.
The rest of the paper is organized as follows. In
Section 2 the WSN is described and the layout prob-
lem is formulated. Section 3 presents the ACO algo-
rithm. In Section 4 the experimental results obtained
5
Fidanova S., Marinov P. and Alba E..
ACO FOR OPTIMAL SENSOR LAYOUT.
DOI: 10.5220/0003057600050009
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 5-9
ISBN: 978-989-8425-31-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

are shown. Finally, several conclusions are drown in
Section 5.
2 PROBLEM FORMULATION
A Wireless Sensor Network is a wireless network
formed by sensor nodes. Each sensor node sens an
area around itself called its sensing area. A parameter
called sensing radius determines the sensitivity range
of the sensor node and thus the sensing area. The
nodes communicate among themselves using wireless
communication links. These links are determined by
a communication radius. A special node in the WSN
called High Energy Communication Node (HECN) is
responsible for external access to the network. There-
fore, every sensor node in the network must have
communication with the HECN. Since the communi-
cation radius is often much smaller than the network
size, direct links are not possible for peripheral nodes.
A multi-hop communication path is then established
for those nodes that do not have the HECN within
their communication range.
The WSN layout problem amounts to deciding the
geographical position of the sensor nodes that form
a WSN. In our formulation, a non-fixed amount of
sensor nodes has to be placed in a terrain providing
full sensitivity coverage. The positions of the nodes
have to be chosen in a way that minimizes the total
number of sensor nodes, while keeps the connectivity
of the network.
The WSN operates by rounds: In a round, ev-
ery node collects the data from its measurements and
sends it to the HECN. Every node transmits the infor-
mation packets to the neighbor that is closest to the
HECN, or the HECN itself if it is within the commu-
nication range. The sensing area of the WSN is the
union of the individual areas of all nodes. The de-
signer wants the network to cover the complete sens-
ing area. On the other hand, the number of sensor
nodes must be kept as low as possible, since using
many nodes represents a high cost of the network,
possibly influences of the environment and also pro-
vokes a probability of detection (when stealth moni-
toring is designed). The objective of this problem is
to minimize the number of sensors deployed while the
area is fully covered and connected.
3 ANT COLONY OPTIMIZATION
FRAMEWORK
Many of the existing solutions to this problem come
from the field of Evolutionary Computation (Alba and
Molina, 2008; Molina et al., 2008). After analyz-
ing them, we noticed that these interesting develop-
ments are quite similar to ACO algorithms. The re-
lation between ACO algorithms and evolutionary al-
gorithms provides a structural way of handling con-
strained problems. They have in common the use of
a probabilistic mechanisms for recombination of in-
dividuals. This leads to algorithms where the popula-
tion statistics are kept in a probability vector. In each
iteration of the algorithm, these probabilities are used
to generate new solutions. The new solutions are then
used to adapt the probability vector.
Real ants foraging for food lay down quantities
of pheromone (chemical cues) marking the path that
they follow. An isolated ant moves essentially guided
by an heuristic function and an ant encountering a
previously laid pheromone will detect and decide to
follow it with high probability thus taking more in-
formed actions based on the experience of previous
ants (and thereby reinforce it with a further quantity
of pheromone). The repetition of the above mecha-
nism represents the auto-catalytic behavior of real ant
colony where the more the ants followa trail, the more
attractive that trail becomes.
The ACO algorithm uses a colony of artificial ants
that behave as cooperative agents in a mathematic
space were they are allowed to search and reinforce
pathways (solutions) in order to find the optimal ones.
The problem is represented by graph and the ants
walk on the graph to construct solutions. The so-
lution is represented by a path in the graph. After
initialization of the pheromone trails, ants construct
feasible solutions, starting from random nodes, then
the pheromone trails are updated. At each step ants
compute a set of feasible moves and select the best
one (according to some probabilistic rules based on a
heuristic guided function) to carry out the rest of the
tour. The structure of ACO algorithm is shown in Fig-
ure 1. The transition probability p
ij
, to chose the node
j when the current node is i, is based on the heuristic
information η
ij
and on the pheromone trail level τ
ij
of the move, where i, j = 1, . . . . ,n.
p
ij
=
τ
α
ij
η
β
ij
∑
k∈allowed
τ
α
ik
η
β
ik
(1)
The higher value of the pheromone and the heuris-
tic information, the more profitable is to select this
ICEC 2010 - International Conference on Evolutionary Computation
6

move. In the beginning, the initial pheromone level
is set to a small positive constant value τ
0
and then
ants update this value after completing the construc-
tion stage (Bonabeau et al., 1999). ACO algorithms
adopt different criteria to update the pheromone level.
Ant Colony Optimization.
Initialize number of ants;
Initialize the ACO parameters;
while not end-condition do
for k=0 to number of ants
ant k starts from a random node;
while solution is not constructed do
ant k selects higher probability node;
end while
end for
Local search procedure;
Update-pheromone-trails;
end while
Figure 1: Pseudocode for ACO.
In our implementation we use MAX-MIN Ant
System (MMAS) (Stutzle and Hoos, 2000), which is
one of the more popular ant approaches. The main
feature of MMAS is using a fixed upper bound τ
max
and a lower bound τ
min
of the pheromone trails. Thus
the accumulation of big amounts of pheromone by
part of the possible movements and repetition of same
solutions is partially prevented. The main features of
MMAS are:
• Strong exploration to the space search of the best
found solution. This can be achieved by only al-
lowing one single ant to add pheromone after each
iteration (the best one).
• Wide exploration of the best solution. After the
first iteration, the pheromone trails are reinitial-
ized to τ
max
. In the next iteration, only the move-
ments that belong to the best solution receive a
pheromone, while the rest pheromone values are
only evaporated.
The aim of using only one solution is to make the
solution components, which frequently occur in the
best found solutions, get a larger reinforcement. The
pheromone trail update rule is given by:
τ
ij
← ρτ
ij
+ ∆τ
ij
, (2)
∆τ
ij
=
1/C(V
best
) if (i, j) ∈ best solution
0 otherwise
,
Where V
best
is the iteration best solution and i, j =
1,...,n, ρ ∈ [0,1] models evaporation in the nature.
To avoid stagnation of the search, the range of pos-
sible pheromone values on each movement is lim-
ited to an interval [τ
min
,τ
max
]. τ
max
is an asymptotic
maximum of τ
ij
and τ
max
= 1/(1 − ρ)C(V
∗
), while
τ
min
= 0.087τ
max
. Where V
∗
is the optimal solution,
but it is unknown, therefore we use V
best
instead of
V
∗
.
The WSN layout problem is represented by graph
as follows: the terrain is modeled by grid G =
{g
ij
}
N×M
; the pheromone is related with location
sites Ph = {ph
ij
}
N×M
, the initial pheromone can be
a small value, for example 1/n
ants
. The central point,
where the HECN is located, is included in the solu-
tions like first point (zero point). Every ant starts to
create the rest of the solution from a random node
which communicates with central one, thus the differ-
ent start of every ant in every iteration is guaranteed.
The ant chooses the next position by the ACO prob-
abilistic rule (equation 1). It choses the point having
the higher probability.
The used heuristic information is
η
ij
(t) = s
ij
l
ij
(1− b
ij
), (3)
where s
ij
is the number of points which the new sen-
sor will cover, and
l
ij
=
1 if communication exists
0 if there is not communication
(4)
b is the solution matrix and the matrix element
b
ij
= 1 when there is sensor on this position other-
wise b
ij
= 0. With s
ij
we try to locally increase the
covered points, with l
ij
we guarantee that all sensors
will be connected; with rule (1 − b
ij
) we guarantee
that the position is not chosen yet. When p
ij
= 0 for
all values of i and j the search stops. Thus, the con-
struction of the solution stops if no more free posi-
tions, or all points are covered or new communication
is impossible.
4 EXPERIMENTAL RESULTS
In this work we solve an WSN problem instance
where a terrain of 500 × 500 meters has to be cov-
ered using nodes with coverage and communication
radii equal to 30 meters. An example of solution that
achieves full coverage of the region is a square grid
formed by the sensors separated by 30 meters.Thus,
the number of sensors is 289 including the HECN.
This result is used for comparison. We apply MAX-
MIN ant algorithm with the following parameters:
ACO FOR OPTIMAL SENSOR LAYOUT
7
α = β = 1, ρ = 0.5, the number of used ants is 3 and
the maximum number of iterations is 10. In Table 1
are reported best found results (minimal number of
sensors) achieved by several metaheuristic methods.
We compare our ACO algorithm results with results
obtained by the evolutionary algorithms in (Molina
et al., 2008) and the symmetric solution.
Table 1: Experimental results.
Algorithm sensors
Symmetric 289
MOEA 260
NSGA-II 262
IBEA
HD
265
ACO 232
We observe that the ACO algorithm outperforms
the symmetric and the evolutionary algorithms. We
perform 30 independent runs of the ACO algorithm
and the achieved numbers of sensors are in the in-
terval [232,247]. The ACO algorithm outperforms
the evolutionary algorithms, because the worst found
number of sensors by ACO is less than the best found
by the evolutionary algorithms.
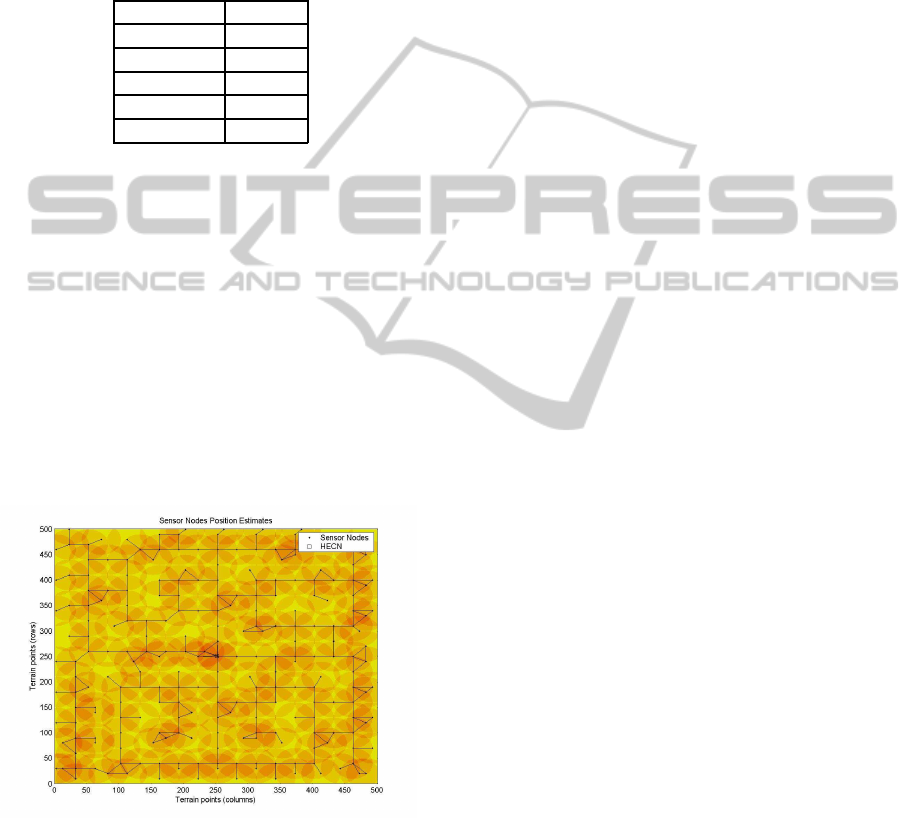
The ACO solution is represented on Figure 2.
With black dots are represented the sensors and with
the rings are represented the coverage and connectiv-
ity area by a sensor. We can observe there the cover-
age of the region, positioning of the sensors and con-
nectivity of the network.
Figure 2: ACO solution.
5 CONCLUSIONS
We have defined a coverage problem for wireless sen-
sor networks with its connectivity constraint. A very
large instance consisting of 500 × 500 square meter
area has to be covered using sensors nodes whose
sensing and communication radii are 30 meters. We
propose ACO algorithm to solve this problem and
we compare it with existing evolutionary algorithms.
The ACO algorithm outperforms the evolutionary al-
gorithms. The worst found solution by ACO is bet-
ter than the best found solution by evolutionary al-
gorithms. In a future work we plane to redefine the
problem so as to be able to solve more complex WSN
layout problem with regions in a sensing area where
to put sensors is forbidden and network problem with
obstacles. Other interesting direction is to study the
robustness of the solutions, to minimize the distur-
bance in the network when single sensor fail and thus
to avid segmentation of the network.
ACKNOWLEDGEMENTS
This work has been partially supported by the Bul-
garian National Scientific Fund under the grants
”Modeling Processes with fixed development rules”
DID 02/29 and ”Effective Monte Carlo Methods
for large-scale scientific problems” DTK 02/44, and
by Spanish Ministry of Science and Innovation
and FEDER under contract TIN2008-06491-C04-
01 (M-project, http://mstar.lcc.uma.es). It has also
been partially funded by the Andalusian Government
under contract P07-TIC-03044 (DIRICOM project,
http://diricom.lcc.uma.es).
REFERENCES
Alba, E. and Molina, G. (2008). Optimal wireless sensor
layout with metaheuristics: Solving a large scale in-
stance. In Large-Scale Scientific Computing, pages
527–535. Springer.
Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999).
Swarm Intelligence:From Natural to Artificial Sys-
tems. Oxford University Press, New York.
Deb, K., Pratap, A., Agrawal, S., and Meyarivan, T. (2000).
A Fast and Elitist Multiobjective Genetic Algorithm:
Nsga-ii.
Jourdan, D. (2000). Wireless Sensor Network Planing with
Application to UWB Localization in GPS-denied En-
vironments. PhD thesis, Masachusets Institut of Tech-
nology.
Molina, G., Alba, E., and Talbi, E.-G. (2008). Opti-
mal sensor network layout using multi-objective meta-
heuristics. Universal Computer Science 14(15), pages
2549–2565.
Paek, J., Kothari, N., Chintalapudi, K., Rangwala, S., and
Govindan, R. (2004). The Performance of a Wireless
Sensor Network for Structural Health Monitoring.
ICEC 2010 - International Conference on Evolutionary Computation
8

Stutzle, T. and Hoos, H. (2000). Max-min ant system. Fu-
ture Generation Computer Systems 16, pages 889–
914.
Werner-Allen, G., Lorinez, K., Welsh, M., Marcillo, O.,
Jonson, J., Ruiz, M., and Lees, J. (2006). Deploying
a wireless sensor network on an active volcano. IEEE
Internet Computing 10(2), pages 18–25.
Yuce, M., Ng, S., Myo, N., Khan, J., and Liu, W. (2007).
Wireless body sensor network using medical implant
band. Medical Systems 31(6), pages 467–474.
ACO FOR OPTIMAL SENSOR LAYOUT
9
