
PROLONGATION RECOGNITION IN DISORDERED SPEECH
USING CWT AND KOHONEN NETWORK
Ireneusz Codello, Wiesława Kuniszyk-Jóźkowiak, Elżbieta Smołka and Adam Kobus
Institute of Computer Science, Maria Curie-Skłodowska University, pl. Marii Curie-Skłodowskiej 1, Lublin, Poland
Keywords: Kohonen network, Automatic prolongation recognition, Waveblaster, Neuron reduction, CWT, Continuous
wavelet transform, Bark scale.
Abstract: Automatic disorder recognition in speech can be very helpful for the therapist while monitoring therapy
progress of the patients with disordered speech. In this article we focus on prolongations. We analyze the
signal using Continuous Wavelet Transform with 22 bark scales, we divide the result into vectors (using
windowing) and then we pass such vectors into Kohonen network. We have increased the recognition ratio
from 54% to 81% by adding a modification into the network learning process as well as into CWT
computation algorithm. All the analysis was performed and the results were obtained using the authors’
program – “WaveBlaster”. It is very important that the recognition ratio above 80% was obtained by a fully
automatic algorithm (without a teacher). The presented problem is part of our research aimed at creating an
automatic prolongation recognition system.
1 INTRODUCTION
Speech recognition is a very important branch of
informatics nowadays – oral communication with a
computer can be helpful in real-time document
writing, language translating or simply in using a
computer. Therefore the issue has been analyzed for
many years by researches, which caused many
algorithms to be created such as Fourier transform,
Linear Prediction, spectral analysis. Disorder
recognition in speech is quite a similar issue – we try
to find where speech is not fluent instead of trying to
understand the speech, therefore the same algorithms
can be used. Automatically generated statistics of
disorders can be used as a support for therapists in
their attempts at an estimation of the therapy
progress.
We have decided to use a relatively new
algorithm – Continuous Wavelet Transform (CWT)
(Akansu and Haddar 2001, Coddello and Kuniszyk-
Jóźkowiak 2007, Nayak 2005), because by using it
we can choose scales (frequencies) which are most
suitable for us (Fourier transform and Linear
Prediction are not so flexible). We have choosen the
bark scales set, which is, besides the Mel scales and
the ERB scales, considered as a perceptually based
approach (Smith and Abel 1999). The CWT result
is divided into fixed-length windows, each one is
converted into a vector and such a vector is passed
into the Kohonen network. Then we use a simple
algorithm on the Kohonen output to determine if this
window contains prolongation or not. This way we
obtain the list of the windows in which
prolongations occurred.
After creating recognition statistics we decided
to add a few algorithm improvements which
signifficantly increased the recognition ratio.
2 CWT
2.1 Mother Wavelet
Mother wavelet is the heart of the Continuous
Wavelet Transform.
t
baba
ttxCWT )()(
,,
(1)
a
bt
a
t
ba
1
)(
,
(2)
where x(t) – input signal, ψ
a,b
(t) – wavelet family,
ψ(t) – mother wavelet, a – scale (multiplicity of
mother wavelet), b – offset in time.
392
Codello I., Kuniszyk-JóÅžkowiak W., Smołka E. and Kobus A..
PROLONGATION RECOGNITION IN DISORDERED SPEECH USING CWT AND KOHONEN NETWORK.
DOI: 10.5220/0003057903920398
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
392-398
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

We used Morlet wavelet of the form
(Goupillaud, Grossmann, Morlet, 1984-1985):
)202cos()(
2/
2
tet
t
(3)
which has center frequency F
C
=20Hz. Mother
wavelets have one significant feature: length of the
wavelet is connected with F
C
which is a restraint for
us. Morlet wavelet is different because we can
choose its length and then set its F
C
by changing the
cosines argument.
2.2 Scales
For frequencies of scales we decided to assume a
perceptually based approach – because it is
considered to be the closest to the human way of
hearing. We choose Hartmut scales (Traunmüller
1990):
53.0
/19601
81.26
f
B
, f – freq. in Hz
(4)
The frequency of each wavelet scale a was
computed from the equation
aFFF
SCa
/ , F
S
– sampling frequency
(5)
Due to the discrete nature of the algorithm, it was
not always possible to match scale a with scale B
perfectly (Table 1).
Table 1: 22 scales a (and scale’s shift b) with
corresponding frequencies f and bark scales B.
a [scale] f [Hz] B [bark] b [samples]
46 9586 21,7 23
57 7736 20,9 29
68 6485 20,1 34
83 5313 19,1 42
100 4410 18 50
119 3705 17 60
140 3150 16 70
163 2705 15 82
190 2321 14 95
220 2004 13 110
256 1722 12 128
297 1484 11 149
347 1270 10 174
408 1080 9 204
479 920 8 240
572 770 7 286
700 630 6 350
864 510 5 432
1102 400 4 551
1470 300 3 735
2205 200 2 1103
4410 100 0,8 2205
2.3 Smoothing Scales
Because CWT values are similarity coefficients
between signal and wavelet, we assumed that the
sign of its value is irrelevant, therefore in all
computations modules are taken – |CWT
a,b
|. We
went one step further and we smoothed the |CWT
a,b
|
by creating a contour (see Figure 2)
1
Figure 1: Cross-section of one CWT
a,b
scale.
1
Figure 2: Cross-section of one |CWT
a,b
| scale and its
contour (smoothed version).
2.4 Windowing
Thus now we have spectrogram consisting of 22
smoothed bark scales vectors. Then we cut the
spectrogram into 23.2ms frames (512 samples when
F
S
=22050Hz), with a 50% frame offset. Because
every scale has its own offset – one window of fixed
width (e.g. 512 samples) will contain different
number of amplitudes (CWT similarity coefficients)
in each scale (see Figure 3), therefore we take the
arithmetic mean of each scale's amplitudes.
Figure 3: One CWT window (512 samples when
F
S
=22050Hz).
From one window we obtain the vector V of the
form:
6
44102205
5746
,...,
,,
CWTmeanCWTmean
CWTmeanCWTmeanV
(6)
Such consecutive vectors are then passed into the
Kohonen network.
3 KOHONEN NETWORK
The Kohonen network (Kohonen T, 2001, Garfield
PROLONGATION RECOGNITION IN DISORDERED SPEECH USING CWT AND KOHONEN NETWORK
393

S. 2001) (or "self-organizing map", or SOM, for
short) was developed by Teuvo Kohonen. The basic
idea behind the Kohonen network is to establish a
structure of interconnected processing units
("neurons") which compete for the signal. While the
structure of the map may be quite arbitrary, we use
rectangular maps.
Let assume that:
Kohonen network has K neurons
n is dimension of each input vector X
each element
Xx
i
is connected to all K
neurons, so we have
nK connections. Every
connection is represented by it’s weight w
ij
,
i=1..n, j=1..K which are adjusted during the
training.
We use the Kohonen network to convert 3-
dimention CWT spectrogram into 2-dimention
winning neuron contour (Szczurowska and
Kuniszyk-Jóźkowiak, 2006, 2007)
3.1 Learning Algorithm
The basic training algorithm is quite simple:
select the input vector from the training set – we
could take consecutive vectors, or take them
randomly
find the neuron which is closest to the given
input vector (i.e. the distance between
niwW
ijj
..1: and X is a minimum). The
metric can be arbitrary, usually Euclidean, where
the distance between the input vector and i-th
neuron is defined:
,
1
2
n
j
ijji
wxd
(7)
adjust the weight vectors of the closest node and
the nodes around it in a way that they move
towards the training data:
jjj
WXWW
(8)
, α is a coefficient factor, usually connected with the
distance from the winning neuron
repeat all steps for a fixed number of repetitions
As a result of such learning, we can say that, in a
Kohonen map, neurons located physically next to
each other will correspond to classes of input vectors
that are likewise next to each other (Figure 4).
Therefore such regions are called maps.
3.2 Learning Algorithm Modification
We added one additional step into the learning
process (Codello and Kuniszyk-Jóźkowiak 2010).
This step is applied after the network has been
trained using the standard algorithm described
previously. The purpose is to reduce each map
(which contains similar neurons) to only one neuron
within one map.
We do the following:
Find two closest neurons k
A
, k
B
(the distance
between neurons weights are measured using
Euclidean metric – equation 7.)
If the distance is less then some threshold
(algorithm’s parameter), fill weights of one of
the neurons with zeros. This way input vectors
that were assigned to k
B
neuron, now will be
assigned to k
A
Repeat steps 1. and 2. until there exists a pair of
neurons closer then the threshold.
The result of the reducing procedure is shown in
Figures 5 and 6. As we can see, such a result is
much clearer and therefore more useful than an
unmodified result.
Figure 4: Input vectors with corresponding maps on
Kohonen network before (top) and after (bottom) "neuron
reduction". Similar vectors are assigned to group of
neurons (top) and to only one neuron (bottom). Other
neurons (white ones) within the maps are cleared.
ICFC 2010 - International Conference on Fuzzy Computation
394
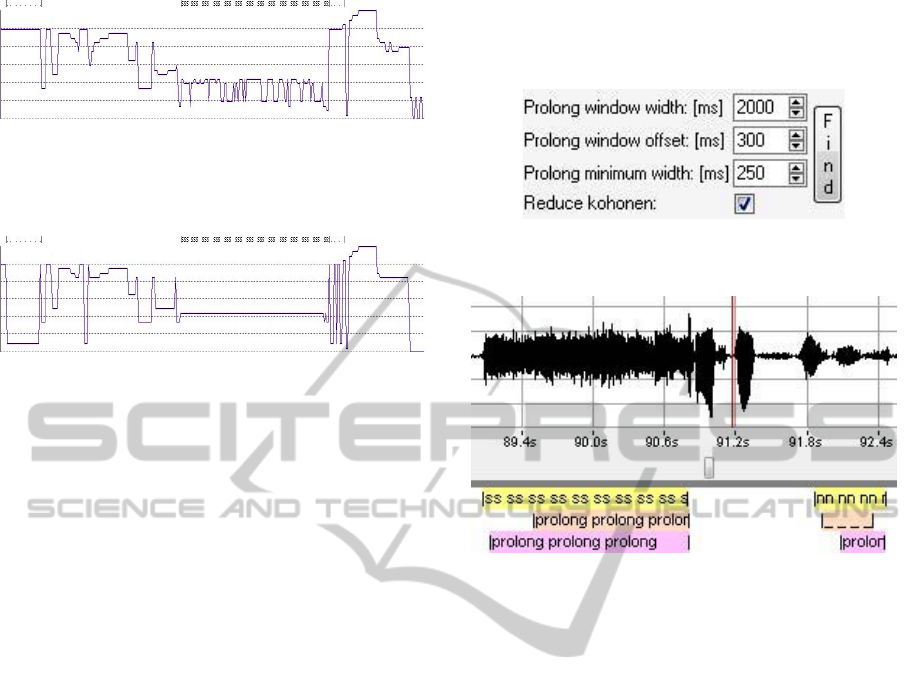
Figure 5: Winning neuron contour of the 2 seconds long
utterance with prolongation “sss”. Kohonen network size:
5x5. Vertical axis: winning neuron number, horizontal
axis: time. Screenshot from program “WaveBlaster”.
Figure 6: Winning neuron contour from Figure 5 after
"neuron reduction". Screenshot from program
“WaveBlaster”.
4 AUTOMATIC PROLONGATION
RECOGNITION
The procedure of finding prolongations in the file is
the following:
Compute CWT spectrogram for the entire file
Divide the spectrogram into ‘small’ windows
(e.g. 23.2 ms) with a certain offset (e.g. 11.6 ms).
By using windowing (see section 2.4 for details)
each ‘small’ window is converted into a set of 22
element vectors (each vector’s element
corresponds to one bark scale)
Divide the result into ‘big’ windows (e.g.
2000ms – first parameter on Figure 7) with a
certain shift (e.g. 300ms – second parameter on
Figure 7)
Each window, which consists of 22-element
vectors, is passed into the Kohonen network.
After the learning process we obtain a winning
neuron graph (Figure 5)
Then we can perform the Kohonen neuron
reduction (fourth option in Figure 7)
If a winning neuron contour (Figure 6) contains a
section longer then a certain parameter (e.g.
250ms – the third parameter in Figure 7) in
which only one neuron wins – then this section is
considered as prolongation
If the section overlaps some other automatically
found prolongation, then the sections are
combined
At the end we manually compare the pattern with
the algorithm output and count the number of
correctly and incorrectly recognized prolongation
(Figure 8)
Figure 7: Automatic prolongation options panel.
Screenshot from program “WaveBlaster”.
Figure 8: Input signal with three sets of patterns (first one
manually created, other two automatically generated by
algorithm with different configuration) – screenshot from
program WaveBlaster.
5 WAVEBLASTER
The presented way of Kohonen post-learning and
CWT smoothing is quite unique, therefore we had to
create our own tool for this purpose. The presented
problem is only part of our research (an automatic
prolongation recognition system) – therefore our
program ’WaveBlaster’ has quite a developed
functionality and set of parameters.
The following algorithms are implemented:
DTF, iDFT, FFT, iFFT
FFT reduced by 1/3 octave filters
Linear Prediction (LP)
Formant tracking (based on LP)
Vocal tract visualization (based on LP)
Signal envelope calculation
DWT, CWT
Kohonen neural network
Automatic
The following graphs are displayed:
DFT, FFT, 1/3 octave FFT, LP, DWT and CWT
PROLONGATION RECOGNITION IN DISORDERED SPEECH USING CWT AND KOHONEN NETWORK
395

2D spectrums and 3D spectrograms
LP parameters and formant paths
3D vocal tract visualization
Kohonen neural network
Wavelets and wavelet scales
All the modules, despite of the numerous
elements, are consistent. The components are
flexibly programmed, enabling the user to easily
change and visualize the data – which is very useful
in research processes during which, when we look
for the answers and some regularity, we need to look
at the same set of data from different perspectives
(enlarging, reducing, shifting, selecting, changing
colors, scales, different analysis). The precise system
of axis scales and variety of quantity measurement is
very helpful in the observation process and finding
even small irregularities in data behavior. All graphs
are connected to each other (enlarging, reducing,
shifting and selecting affects all panels) and
therefore for a particular fragment we can observe
many coefficients simultaneously (oscillogram,
spectrograms, spectrums) – which is also quite
helpful while doing research.
Summarizing – all these features make our
application a very useful research tool. It is focused
only on a particular sort of computation – which is
both an advantage and a disadvantage. All this can
be done by other tools, like MATLAB, but we
would not have been able to do it so quickly and
comprehensively (in the context of our needs).
Therefore we think that despite the effort made to
implement this tool, it was worth it – it will be used
in many situations, facilitating and speeding up the
research.
6 RECOGNITION EFFICIENCY
ANALISYS
6.1 Input Data
We took Polish disordered speech recordings of 6
persons and Polish fluent speech recordings of 4
persons. In the disordered speech recordings we
chose all prolongations with 4 seconds surroundings
and from fluent speech we randomly chose several 4
seconds long sections. We merged all the pieces
together obtaining 15 min 24 s long recording
containing 286 prolongations. The statistics are the
following:
Table 2: Prolongations count.
a
5
s
63
e
2
sz
13
f
10
ś
37
g
1
u
2
h
7
w
32
i
7
y
17
j
1
z
43
m
10
ź
6
n
5
ż
17
o
8
all
286
6.2 Algorithm Parameters
In CWT we used Morlet wavelet (equation 3) with
22 Hartmut bark scales (Table 1).
Vectors for the Kohonen network were created
from CWT spectrogram frames divided into 23.2ms
windows shifted by 50% of frame length (11.6 ms) –
for details see paragraph 2.4.
We used a 5x5 Kohonen network with the
following learning parameters: 100 epochs, learning
coefficient 0.10-0.10, neighbor distance 1.5-0.5,
reducing distance 0.30.
An automatic prolongation recognition algorithm
was run with the following settings: prolongation
window equal 2s, offset equal 300ms and minimum
prolongation equal 250ms.
The recognition ratio was calculated using the
formulas (Barro and Marin 2002):
BP
P
litypredictabi
A
P
ysensitivit
(9)
where P is the number of correctly recognized
prolongations, A is the number of all prolongations
and B is the number of fluent sections mistakenly
recognized as prolongation.
6.3 Results
We wanted to test the following two issues:
how the neuron reducing algorithm (see section
3.2 for details) influences the recognition ratio
how the CWT smoothing algorithm (see section
2.3 for details) influences the recognition ratio
Therefore we performed the following four tests:
CWT smoothing: NO, Kohonen network neuron
reduction: NO
CWT smoothing: NO, Kohonen network neuron
ICFC 2010 - International Conference on Fuzzy Computation
396

reduction: YES
CWT smoothing: YES, Kohonen network neuron
reduction: NO
CWT smoothing: YES, Kohonen network neuron
reduction: YES
The results are presented in Table 3.
Table 3: Automatic prolongation recognition results.
1. CWT smoothing – NO, Kohonen reduction – NO
A P B
sensitivity predictability
286 154 8
54% 95%
2. CWT smoothing – NO, Kohonen reduction – YES
A P B
sensitivity predictability
286 179 12
63% 94%
3. CWT smoothing – YES, Kohonen reduction – NO
A P B
sensitivity predictability
286 213 44
74% 83%
4. CWT smoothing – YES, Kohonen reduction – YES
A P B
sensitivity predictability
286 231 48
81% 83%
7 CONCLUSIONS
As we can see, the CWT smoothing algorithm
increased the recognition ratio from 54% (set 1.) to
74% (set 3.) and from 63% (set 2.) to 81% (set 4.). It
gives us 20% and 18% – that is very good. The
CWT algorithm is too precise – especially in the hi-
frequency scales. For the prolongation finding
purpose such precision it is too high – that is why
smoothing gives such a good ratio improvement.
The disadvantage of this method is that it decreases
predictability by 12% (set 1 and 3) and 11% (set 2
and 4), therefore it needs to be improved.
The Kohonen neuron reduction algorithm is a
little more difficult to interpret. We used such an
algorithm because if a prolongation is long (e.g.
1000ms), then consecutive vectors within that period
are similar to each other – they represent one
phoneme. We observed that when we want to have
only one winning neuron for that phoneme, then
other neurons have to compete for other phonemes,
therefore
A) all input vectors representing the prolongation
have to be almost identical, then no matter how
big the network, only one neuron will win the
competition for the prolongation phoneme or
B) an input signal needs to have a few other pho-
nemes in the window (proportional to the size of
the network) – then every neuron in the network
will compete for a different phoneme
When a given prolongation is short, then usually
there are a few phonemes within the window,
therefore condition B is met, which is good. But if
the prolongation is long, or there is a lot of silence,
then there are not many phonemes in the window.
The Kohonen neurons start to compete for the same
phoneme and they specialize in different variations
of one phoneme, which is bad because we want only
one neuron to win. That is why the CWT smoothing
algorithm works so well – it makes similar vectors
even more similar to each other and then condition A
is met. And that is why the ‘neuron reduction’
algorithm is working – it reduces excessive neurons
(condition B is met).
As we can see, ‘neuron reduction’ increases the
recognition ratio by 9% (set 1 and 2) and by 7% (set
3 and 4), which is significant. What is important is
that it does not reduce predictability – it means that
the algorithm improves recognition without
increasing the number of algorithm mistakes.
The results are promising. Now the main issues
are:
to improve the CWT smoothing algorithm – it
decreases predictability ratio too much
to investigate the Kohonen learning parameters
for better prolongation recognition such as: the
Kohonen network size, Kohonen network
learning and neighbour coefficients, Kohonen
network neuron initialization method, wavelet
scales and scale shifts, decibel threshold. The
research into the parameters is in progress.
REFERENCES
Akansu A.N, Haddad R. A., 2001, Multiresolution signal
decomposition, Academic Press.
Barro S., Marin R., 2002, Fuzzy Logic in Medicine,
Physica-Verlag Heidenberg, New York
Codello I., Kuniszyk-Jóźkowiak W., 2007, Wavelet
analysis of speech signal, Annales UMCS Informatica,
2007, AI 6, Pages 103-115.
Codello I., Kuniszyk-Jóźkowiak W., Kobus A., 2010,
Kohonen network application in speech analysis
algorithm, Annales UMCS Informatica, (Accepted
paper).
Garfield, S., M. Elshaw, and S. Wermter. 2001, Self-
orgazizing networks for classification learning from
normal and aphasic speech. In The 23rd Conference of
the Cognitive Science Society. Edinburgh, Scotland
Gold, B., Morgan, N., 2000. Speech and audio signal
PROLONGATION RECOGNITION IN DISORDERED SPEECH USING CWT AND KOHONEN NETWORK
397

processing, JOHN WILEY & SONS, INC.
Goupillaud P., Grossmann A., Morlet J., 1984-
1985.`Cycle-octave and related transforms in seismic
signal analysis'', Geoexploration, 23, 85-102
Huang, X., Acero, A., 2001. Spoken Language Processing:
A Guide to Theory, Algorithm and System
Development, Prentice-Hall Inc.
Kohonen, T., 2001, Self-Organizing Maps, 34:p.2173-
2179
Nayak J., Bhat P. S., Acharya R., Aithal U. V., 2005,
Classification and analysis of speech abnormalities,
Volume 26, Issues 5-6, Pages 319-327, Elsevier SAS
Smith J., Abel J, 1999, Bark and ERB Bilinear
Transforms, IEEE Transactions on Speech and Audio
Processing, November, 1999.
Szczurowska, I, W. Kuniszyk-Jóźkowiak, and E. Smołka,
2006,The application of Kohonen and Multilayer
Perceptron network in the speech nonfluency analysis.
Archives of Acoustics. 31 (4 (Supplement)): p. 205-
210
Szczurowska, I, W. Kuniszyk-Jóźkowiak, and E. Smołka,
2007, Application of Artificial Neural Networks In
Speech Nonfluency Recognition. Polish Jurnal of
Environmental Studies, 2007 16(4A): p. 335-338.
Traunmüller H., 1990 "Analytical expressions for the
tonotopic sensory scale" J. Acoust. Soc. Am. 88: 97-
100.
ICFC 2010 - International Conference on Fuzzy Computation
398
