ESTIMATION OF QUANTUM TIME LENGTH

FOR

ROUND-ROBIN

SCHEDULING ALGORITHM

USING NEURAL

NETWORKS

Omar AlHeyasat and Randa Herzallah

FET, AL-Balqa’ Applied University, Amman, Jordan

Keywords: Round-robin Scheduling Algorithm, Neural Networks Model, Quantum Time, Length Estimation.

Abstract: The quantum time length is usually taken as a fixed value in all applications that use Round Robin (RR)

scheduling algorithm. The determination of the optimal length of the quantum that results in a small average

turn around time is very complicated because of the unknown nature of the tasks in the ready queue. The

round robin algorithm becomes very similar to the first in first served algorithm if the quantum length is

large. On the other hand, high context switch results for small values of quantum length which might cause

central processing unit (CPU) thrashing. In this paper we propose a new RR scheduling algorithm based on

using neural network models for predicting the optimal quantum length that yields minimum average turn

around time. The quantum length is taken to be a function of the service time of the various jobs available in

the ready queue. This in contrast to the traditional methods of using fixed quantum length is shown to give

better results and to minimize the average turnaround time for almost any collection of jobs in the ready

queue.

1 INTRODUCTION

CPU scheduling is the task of selecting a waiting

process from the ready queue and allocating the

CPU to it. The CPU is allocated to the selected

process by the dispatcher. First-come, first-served

(FCFS) schedul- ing is the simplest, but it can cause

short processes to wait for every long process.

Shortest job-first (SJF) scheduling provably optimal,

providing the shortest average waiting time.

Implementing SJF scheduling is difficult, however,

because predicting the length of the next CPU burst

is difficult. The SJF algorithm is a special case of the

general priority scheduling algorithm, which simply

allocates the CPU to the highest priority process.

Both priority and SJF may suffer from starvation.

Round-robin scheduling is more appropriate for a

time-shared (interactive) system. RR scheduling

allocates the CPU to the first process in the ready

queue for q time units, where q is the time quantum.

After q time units, if the process does not relinquish

the CPU, it is preempted, and then it is put at the tail

of the ready queue. Round Robin scheduling

algorithm is considered the fairness compromise

algorithm among different mechanisms and

disciplines that deal with sharing the CPU time

between processes that resides in the ready queue.

RR, First come first served, high priority, shortest

job first and other algorithms have several

disadvantages when dealing with real-time systems

and deadline limitations. In real-world of time-

sharing systems, RR service (behavior) is widely

used.

Many publications discussed the RR scheduling

algorithm, its efficiency, reliability, and its consis-

tency if it was part of a general system. Ramab-

hadran et al (Ramabhadran and Pasquale, 2006) pre-

sented analytical and simulation results based on RR

algorithm in a manner of a stratified RR scheduler.

Jorge R. et al (Ramos et al., 2006) showed a modi-

fied RR algorithm that predicts potential job depar-

tures and schedules them in advance. John Tsili-

garidis et al (Tsiligaridis and Acharya, 2005) dis-

cussed a very important algorithm that constitutes an

alternative way of defining the most suitable size of

the quantum in RR scheduling algorithm using grad-

ual or direct weight increase mechanisms, and in the

same paper the author strongly stated that this kind

of algorithms can be applied for next generation

internet routers. Seungmin Baek et al (Seungmin et

al, 2004) described a packet filtering-based RR

scheduling scheme for tightly coupled clusters in

253

AlHeyasat O. and Herzallah R..

ESTIMATION OF QUANTUM TIME LENGTH FOR ROUND-ROBIN SCHEDULING ALGORITHM USING NEURAL NETWORKS .

DOI: 10.5220/0003058002530257

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages

253-257

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

terms of throughput and reliability. Rahul Garg et al

(Rahul and Xiaoqiang, 1999) described a scheduling

algorithm named recursive round robin scheduler

(RRR), based on the concept of the construction of

scheduling tree, and showed that the work

conserving scheduler is fair. While in (Salil et al.,

2004), Salil et al used a technique to analytically

derive the latency bound of preordered DDR. Many

other publications described, discussed, and proved

many scheduling algorithms (Philip and Rasch,

1970; Ben et al., 2005; Janche et al., 1994; Amotz et

al., 2004; Andrews and Zhang, 2005; Cooling and

Tweedale, 1997; Srinivasan and Anderson, 2005;

Silberschatz et al., 2000; Chakrabarti et al., 1997).

Almost in all these publications, authors selected

different criteria, like fairness, bounded delay, low

complexity, deadline and other criteria. The

common among almost all works (Tsiligaridis and

Acharya, 2005; Seungmin et al., 2004; Rahul and

Xiaoqiang, 1999; Salil et al., 2004) that discussed

RR scheduling algorithm is that the length of

quantum time is fixed.

The major problem in RR scheduling is the

selection of the time quantum. If the quantum is too

large, RR scheduling degenerates to FCFS

scheduling. If jobs. Figure 1 Shows the block

diagram of the pro- posed RR scheduling algorithm.

Here neural network model is used to estimate and

predict the time quantum based on the service time

of the jobs in the queue. Using neural network

model to estimate the time quantum has the

advantage of varying the time quantum according to

the variation of the service time of the jobs in the

ready queue. Instead of using fixed quantum time,

neural network model estimates and predict the time

quantum that minimizes the average turnaround

time.

Figure 1: The architecture of the proposed scheduling

algorithm.

2 PROBLEM FORMULATION

In RR scheduling algorithm, the average turnaround

time is described by the following equation:

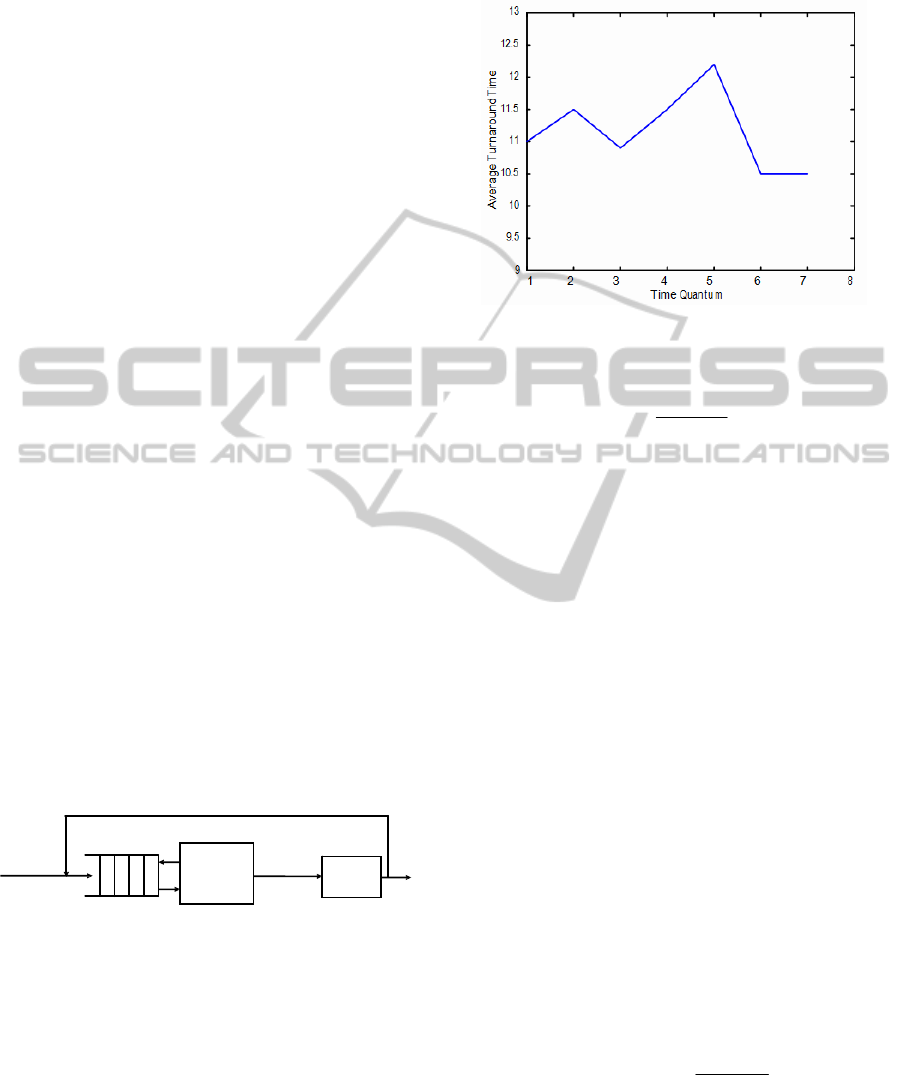
the quantum is too small, scheduling overhead in the

form of context-switch time becomes excessive. In

addition, the turnaround time can varies with

different time quantum. Figure 2 Shows the way in

which turnaround time varies with the time quantum.

Figure 2: The variation of the turnaround time with the

time.

∑

(1)

where T

is the average turnaround time,

is the

service time of job i in the ready

queue,

is the

waiting time of job i in the ready queue, and N is the

number of jobs in the ready queue.

The objective in this paper is to minimize the av-

erage turnaround time by the control of the optimal

quantum time length q. By changing the quantum

time length the average waiting time of the various

jobs in the ready queue will be different. The aver-

age waiting time can be described as a function of the

quantum time length according to the following equa-

tion

(

)

oqNW

(2)

where o is the context time switch. In practical appli-

cations it is desirable to make the context switch neg-

ligible compared to the quantum time length. Taking

this into consideration and substituting Equation (2)

into Equation (1) yields

quantum

In this paper, we will develop a neural network

model that will estimate the time quantum for the

Round-robin scheduling algorithm, in order to min-

imize the turnaround time for any collection of ready

∑

Nqs

(3)

Equation (3) shows that the average turnaround

time highly depends on the value of the selected

quantum length, which in turn is dependent on the

service time of the jobs in the ready queue.

Arrival jobs

Ready Queue

Neural

Network

Model

Quantum

length

CPU

ICFC 2010 - International Conference on Fuzzy Computation

254

Following this, the RR scheduling problem can be

described as follows:

Find the time quantum length q such that the fol

lowing objectives are met:

1. The turnaround time of a set of jobs in the ready

queue is minimized.

2. The number of context switch is kept minimal.

3 NEURAL NETWORK MODEL

The effect of the service time on the length of the

quantum is characterized by high levels of

uncertainty and complexity. Neural network

models are proved to give superior results under

such circumstances. consequently, in this paper we

propose using neural network models to estimate

and predict the optimal length of the time quantum

that will give the minimum turnaround time for

various service times of the jobs in the ready queue.

Neural Network models with nonlinear compo-

nents can be used in nonlinear, complex and uncertain

applications. The inherently parallel nature of the net-

works can make them suitable for solving problems

at high rates. The important result that multi-layer

feed-forward networks with a single hidden layer and

sufficient number of hidden units, are capable of ap-

proximating any continuous function to any degree of

accuracy has been proved in the literature. Therefore,

in this paper, multi layer perceptron neural network

with one hidden layer will be used. The number of

neurons in the input layer are determined by the num-

ber of jobs in the ready queue. Here the output of the

neural network is the quantum length that results into

minimum turnaround time. This architecture is shown

in Figure 3. The hidden layer activation function is

taken to be tanh function and the activation function

of the output layer is taken to be linear function.

The design of a neural network model involves

Two major phases: Training and validation. In the

training phase the weight parameters of the neural

network model are determined using a set of input–

output patterns in the training set. The neural net-

work model is trained such that it minimizes the mean

square error between the estimated quantum value

and the actual one. Scaled conjugate gradient method

is employed in this work to optimize the weight pa-

rameters. To find the network structure that has the

best performance on new data, different structures of

neural network models are firstly trained using the

training set. The performance of the various struc-

tures of the network models is then compared by eval-

uating an error function using an independent

validation set, and the network having the smallest

error with respect to the validation set is selected.

After training and validating the neural network

model, it can be applied on line to predict the quantum

length value that results into the minimum turnaround

time.

To reemphasize, neural network model is pro-

posed in this study to estimate the length of the quan-

tum time that will be used in the RR scheduling al-

gorithm. The neural network model takes the service

time of the jobs in the ready queue as input and esti-

mates the length of the time quantum that gives min-

imum turnaround time. As a result of the dynamic

changes of the quantum, the average turnaround time

for almost all the jobs should be the minimal. Con-

trast to conventional methods of RR scheduling algo-

rithm which use fixed quantum length, the proposed

RR scheduling algorithm is shown to give superior

results and to minimize the turnaround time in almost

all sets of jobs in the ready queue.

Figure 3: A multilayer feedforward neural

network.

4 SIMULATION RESULTS

In this section neural network model is used to pre-

dict the optimal quantum length that gives minimum

turnaround time. The number of jobs in the ready

queue is taken to be ten. The service time of the

jobs are generated randomly to have values between

1.0 and 10.0. Ten thousand samples of the ten jobs

are simulated. Here, for each sample (consisting of

10 jobs) the average turnaround time is calculated for

fifty different values of quantum time length starting

from 0.1 and stepping up to 5.0 at a step of

Multi layer perceptron neural network with the

Quantum length that gives

minimum average

turnaround time

Output

layer

Hidden

layer

Input

layer

Service time of various

jobs in the ready queue

ESTIMATION OF QUANTUM TIME LENGTH FOR ROUND-ROBIN SCHEDULING ALGORITHM USING

NEURAL NETWORKS

255

service time of the ten jobs as input and optimal quan-

tum length as output is used to predict the optimal

quantum length to be used in the RR scheduling

algorithm.

()

10321

,,,, SSSSgq

est

where g is multi layer perceptron neural network and

est

is the predicted quantum length from the neural

network model.

Since the service time of the jobs in the ready

queue ranges between 1.0 and 10.0, normalization for

the input variables has been conducted. Here each

input variable is normalized between 0 and 1 by di-

viding the service time of each job by its maximum

value, which is 10 in this simulation example.

Figure 4: The quantum length network validation result.

10.0

max,

nori

Normalization of the output variable is not necessary

in this study since linear activation function is as-

sumed for the output layer.

The neural network model was trained on the

training set which consisted of 5000 samples of the

collected data. Scaled conjugate gradient method was

implemented to obtain the optimal parameters of the

neural network model. The single optimal structure

of the neural network model found by applying the

cross validation method consisted of 31 neurons in the

hidden layer. In the cross validation method the neu-

ral network model that estimates the optimal quantum

length to be used in the RR scheduling algorithm has

been tested on a validation data set which consisted of

2000 samples that have not been seen in the training

stage. The error function between the optimal quan-

tum length and the estimated quantum length from the

neural network model,

est

qqe −=

, was calculated

for different model structures with different number

of neurons in the hidden layer. the best optimal struc-

ture is then taken to be the model with the minimum

error value in the validation stage. The validation re-

sult is shown in Figure 4.

After training the neural network model that pre-

dicts the optimal quantum value off line, and choosing

the structure of the model, the quantum length net-

work is brought on line and the quantum length is

calculated for each set consisting of ten jobs in the

ready queue. The optimal quantum length value and

the estimated one from the neural network model is

shown in Table 1. Comparing the estimated quantum

length value and the optimal one, it can be seen that

the neural network model was able to predict to a very

good accuracy the optimal quantum length that

minimizes the average turnaround time in almost

most of the cases.

5 CONCLUSIONS

In this paper, we have demonstrated for the first time

the application of neural network models to predict

the optimal quantum length in the RR scheduling al-

gorithm. A major feature of using neural network

models to predict the quantum length is the dynamic

change of the quantum length to be used in the RR

scheduling algorithm.

The proposed method is validated using ten thou-

sands samples consist of ten jobs in the ready queue.

Simulation results proved the capability of the neu-

ral network model to predict the optimal quantum

length value that yields minimum average turnaround

time. Contrast to the conventional RR scheduling al-

gorithm which uses fixed quantum length value re-

gardless the knowledge on the service time of the

jobs in the ready queue, our proposed neural network

based RR scheduling algorithm dynamically changes

the quantum length value based on the service time of

the jobs in the ready queue. This has the benefit of

minimizing the overall average turnaround time for

the different set of jobs that might be presented to the

CPU.

Neural network model is brought on line only

after being trained and validated. This means that

compu- tational time of the cpu is kept the same.

The only added time to the CPU is the computation

of the op timal quantum length value from the

neural network model which needs only one

forward propagation of its input vector.

ICFC 2010 - International Conference on Fuzzy Computation

256

Table 1: Estimated and optimal quantum lengths for several sets of services times of the ten jobs in the ready queue.

Quantum

length (q

)

Quantum

length(q)

Job10



Job9

Job8

Job7

Job6

Job5



Job4



Job3



Job2



Job1



4.9932

5.0001.9004.2008.1008.3004.5009.6003.9005.8004.100

3.8118

4.7

3.5002.5004.0001.0001.0006.4009.3004.6002.2003.800

3.0065

2.9

4.7005.1000.1009.6008.1001.4009.70010.0002.0002.900

4.5457

4.9

8.5007.7004.8006.9001.7003.3009.3000.8002.8009.700

4.0042

3.2

7.5009.0002.8006.3007.8003.1008.6007.2002.9006.000

3.971

4.0

3.9009.0008.9001.8008.0005.3002.8005.9007.8008.000

3.4346

3.7

3.7008.6002.6003.4001.1004.8006.30010.0007.1005.300

3.1378

3.1

3.1002.7007.9005.7005.8005.5007.7008.5005.8005.900

3.8003

2.1

5.6000.8007.9008.8001.6004.1005.8006.2006.7008.600

3.8491

4.3

0.3008.7006.7006.1008.2006.3009.3004.3001.0007.700

4.0545

4.0

3.5003.9008.6009.4001.4005.6005.2006.7002.2004.000

2.1449

2.1

1.1005.3003.6002.1001.4006.0006.1005.6008.5005.000

3.5606

3.3

2.7008.0004.0005.6004.7009.6000.2006.6006.5002.600

3.7999

4.6

8.7005.1006.9006.7000.9006.0000.2001.9004.6007.100

2.4572

0.5

0.4004.3006.3009.0008.4001.4000.4003.0007.3000.300

3.3133

4.2

5.8005.7004.2000.8001.4002.0000.2000.3001.9002.600

1.1836

1.3

4.5003.8001.3000.3001.1005.2007.1008.2006.0001.900

4.1698

4.3

1.6005.3002.9005.3004.3004.2000.9005.4004.2005.100

4.6203

4.9

8.6005.5000.4007.5004.8002.0006.2004.9004.5002.200

4.9653

4.6

0.6004.6002.7003.6008.0002.3001.0003.6004.6003.200

3.4902

3.7

6.7002.1003.7003.2004.8005.5005.8006.7009.8007.100

2.5514

2.3

9.0002.1003.5000.1001.4001.5005.5001.8009.7004.400

3.0072

2.9

2.7000.4001.0008.1009.8009.1005.3002.9008.0001.600

3.2077

2.8

1.4005.0004.8005.1009.1008.7005.6007.2007.4004.900

4.1322

4.1

9.6005.1008.7004.1001.0009.2006.7008.1006.1001.800

4.8429

4.9

8.5005.7004.2004.4001.5009.6004.3004.8007.6001.800

4.677

4.9

7.4004.9007.0006.0005.7008.8004.3008.2004.2007.100

REFERENCES

Amotz, B., Vladimir, D., and Boaz, P. (2004). Efficient

algorithm for periodic scheduling. Computer

Networks, 45:155–173.

Andrews, M. and Zhang, L. (2005). Scheduling over a

time-varying user-dependent channel with applications

to high-speed wireless data. Journal of the ACM,

52(5):809–834.

Ben, G., Richard, J., Lipton, Andrea, L., and F, F. (2005).

Estimating the maximum.Journal of Algorithms,

54:105–114.

Chakrabarti, S., Demmel, J., and Yelick, K. (1997).

Models and scheduling algorithms for mixed data and

task parallel programs. Journal of Parallel and

Distributed Computing, 47:168–184.

Cooling, J. and Tweedale, P. (1997). Task scheduler co-

processor for hard real-time systems. Microprocessors

and Microsystems, 20:553–566.

Janche, S., Ke-hsiung, C., and Vernon, R. (1994). Efficient

algorithm for simulating service diciplines. Simulation

Practice and Theory, 1:223–244.

Philip, J. and Rasch (1970). A queuing theory study of

round-robin scheduling of time-shared computer

systems. Journal of Association for Computing

Machinary, 17(1):131–145.

Rahul, G. and Xiaoqiang, C. (1999). Rrr: recursive round

robin scheduler. Computer Networks, 31:1951–1966.

Ramabhadran, S. and Pasquale, J. (2006). The stratified

round robin scheduler: Design, analysis and imple

mentation. IEEE/ACM Transactions on Networking,

14(6):1362–1373.

Ramos, R. J., Rego, V., and Sang, J. (2006). An efficient

burst-arrival and batch-departure algorithm for round-

robin servicestar. Simulation Modelling Practice and

Theory, 14(1):1–24.

Salil, S., Kanhere, and Sethu, H. (2004). Investigated

socket-based rr scheduling scheme for tightly coupled

clusters providing single-name images. Computer

Communications, 27:667–678.

Seungmin, B., Hwakyung, R., and Sungchun, K. (2004).

Investigated socket-based rr scheduling scheme for

tightly coupled clusters providing single-name im-

ages. Journal of Systems Architecture, 50:299–308.

Silberschatz, A., Galvinand, P. B., and Gagne, G. (2000).

Operating System Concepts. John Wiley and Sons,

Inc., New York. London.

Srinivasan, A. and Anderson, J. (2005). Fair scheduling of

dynamic task systems on multiprocessors. Journal of

Systems and Software, 77:67–80.

Tsiligaridis, J. and Acharya, R. (2005). Three new

approaches for adjustment and improvement of the rr

scheduler in a dynamic resource environment.

Computer Communications, 28:929–946.

ESTIMATION OF QUANTUM TIME LENGTH FOR ROUND-ROBIN SCHEDULING ALGORITHM USING

NEURAL NETWORKS

257