A NOVEL ADAPTIVE CONTROL VIA SIMPLE RULE(S) USING

CHAOTIC DYNAMICS IN A RECURRENT NEURAL NETWORK

MODEL AND ITS HARDWARE IMPLEMENTATION

Ryosuke Yoshinaka

, Masato Kawashima

, Yuta Takamura

, Hitoshi Yamaguchi

Naoya Miyahara

, Kei-ichiro Nabeta

, Yongtao Li

and Shigetoshi Nara

Graduate School of Natural Science and Technology, Okayama University

3-1-1 Tsushima-naka, Kita-ku, Okayama 700-8530, Japan

Research Institute for Electronic Science, Hokkaido University, Kita 12-jyo Nishi 7-chome, Kita-ku, Sapporo, Japan

Keywords:

Dynamics, Adaptive control, Recurrent neural network, Hardware implementation, Autonoumous robot, Neu-

romorphic device, Brainmorphic device.

Abstract:

A novel idea of adaptive control via simple rule(s) using chaotic dynamics in a recurrent neural network model

is proposed. Since chaos in brain was discovered, an important question, what is the functional role of chaos

in brain, has been arising. Standing on a functional viewpoint of chaos, the authors have been proposing that

chaos has complex functional potentialities and have been showing computer experiments to solve many kinds

of ”ill-posed problems”, such as memory search and so on. The key idea is to harness the onset of complex

nonlinear dynamics in dynamical systems. More speciﬁcally, attractor dynamics and chaotic dynamics in a

recurrent neural network model are introduced via changing a system parameter, ”connectivity”, and adaptive

switching between attractor regime and chaotic regime depending surrounding situations is applied to realiz-

ing complex functions via simple rule(s). In this report, we will show (1)Global outline of our idea, (2)Several

computer experiments to solve 2-dimensional maze by an autonomous robot having a neural network, where

the robot can recognize only rough directions of target with uncertainty and the robot has no pre-knowledge

about the conﬁguration of obstacles (ill-posed setting), (3)Hardware implementations of the computer experi-

ments using two-wheel or two-legs robots driven by our neuro chaos simulator. Successful results are shown

not only in computer experiments but also in practical experiments, (4)Making pseudo-neuron device using

semiconductor and opto-electronic technologies, where the device is called ”dynamic self-electro optical effect

devices (DSEED)”. They could be ”neuromorphic devices” or even ”brainmorphic devices”.

1 INTRODUCTION

Since chaos is discovered in many natural phenom-

ena, particularly, chaotic dynamics observed in bi-

ological systems including brain suggest us to con-

sider whether there are certain important relations be-

tween chaotic dynamics and their excellent functions

in both information processing and well-regulated

functioning or controlling. (Skarda and Freeman,

1987)(Tsuda, 2001)(Fujii et al., 1996)(Tokuda et al.,

1997).

On the other hand, the rapid progress of robotics

have brought various robots into our life and indus-

try, however, it is still quite difﬁcult for the robots

to perform tasks adaptively in various environments,

whereas biological systems have excellent functions

in both information processing and well-regulated

functioning in various environments. Conventional

methodologies (decomposing a system into parts and

elements) often fall into difﬁculties to face enor-

mous complexity originating from dynamics in sys-

tems with large but ﬁnite degrees of freedom.

Under these situations, biological information and

control processing has suggested that they could work

under novel dynamical mechanism that cause excel-

lent functions in information processing and/or con-

trolling. Therefore, many dynamical models have

been proposed for approaching the mechanisms by

means of large-scale simulation or heuristic meth-

ods. Our work originates from a novel idea to har-

ness the onset of complex nonlinear dynamics in in-

formation processing or control systems, and mainly

study chaotic dynamics in neural networks from the

functional viewpoint. First, Nara & Davis intro-

145

Yoshinaka R., Kawashima M., Takamura Y., Yamaguchi H., Miyahara N., Nabeta K., Li Y. and Nara S..

A NOVEL ADAPTIVE CONTROL VIA SIMPLE RULE(S) USING CHAOTIC DYNAMICS IN A RECURRENT NEURAL NETWORK MODEL AND ITS

HARDWARE IMPLEMENTATION .

DOI: 10.5220/0003058301450155

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages

145-155

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

duced chaotic dynamics into a recurrent neural net-

work model (RNNM) by adjusting only one system

parameter (connectivity among neurons), and they

proposed that constrained chaos could be potentially

useful dynamics to solve complex problem, such as

ill-posed problems (Nara and Davis, 1992). As one

of functional experiments, chaotic dynamics was ap-

plied to solving a memory search task or image syn-

thesis which is set in an ill-posed context (Nara et al.,

1993)(Nara et al., 1995)(Nara, 2003). Furthermore,

the idea is extended to challenging application of

chaotic dynamics to control. Chaotic dynamics in-

troduced in a recurrent neural network model was

applied to control tasks that an object is requested

to solve a two-dimensional maze for catching a tar-

get (Suemitsu and Nara, 2004), or to capture a tar-

get moving along different trajectories (Li and Nara,

2008). From the results of computer experiments,

we consider that complex dynamics/chaotic dynamics

could be useful not only in solving ill-posed problems

but also in controlling of systems with large but ﬁnite

degrees of freedom.

Therefore, in the present paper, we develope our

idea and propose a quasi-layered RNNM consist-

ing of sensing neurons(upper layer) and driving neu-

rons(lower layer). In both layers, chaotic dynamics

are used. This idea is based on the work of Mikami

and Nara who found that chaos has a sensitive re-

sponse property to external input (Mikami and Nara,

2003). Their idea is applied to practical functional ex-

periments to solve 2-dimensional mazes, as shown in

the later sections. We can ﬁnd a corresponding exam-

ple in biological behaviors. For instance, auditory be-

havior of cricket gives a typical ill-posed problem in

biological systems (Huber and Thorson, 1985). Fur-

ther developments are shown about the following top-

ics. They are:

(a) to apply our idea to a roving robot with two legs;

(b) to apply our idea to an arm robot;

and a network of them, and to evaluate them by

computer experiments;

ductor and opto-electronic technologies.

2 CONTROL SYSTEM

2.1 Construction of Control System

The control system mainly consists of a roving robot

with a micro processor unit (MPU), sensing systems

of sound signal from target and of detecting obsta-

cles, a neural chaos simulator, Bluetooth interface be-

tween the robot and the neural chaos simulator, and

a target emitting a speciﬁed sound signal, which is

like a singing male cricket, shown as Fig.1. The

Figure 1: Block diagram of control system.

robot with sensors is shown as Fig.2. It has two driv-

ing wheels and one castor (2DW1C). The robot has

six sensors which can be divided into two parts. One

is the sensing system of detecting obstacles that con-

sists of two ultrasonic sensors which givethe robot the

ability to detect whether an obstacle does exist in front

of the robot without actually touching it. The other is

the sensing system of sound signal from target that

consists of four sets of directional microphone cir-

cuits, which functions as ears of the robot. Four mi-

crophones are set with directing to the front, the back,

the left and the right of the robot, which is shown as

Fig.2(right). In our study, a loud speaker is employed

as the target, and is emitting 3.6KHz sound signal

like a singing cricket. This sound signal is picked

up by these four ears(microphone) with π/2 detect-

ing angle oriented to four directions. Among them,

a sound signal coming from one side might have a

strongest intensity, or be loudest. These four sound

signals are ampliﬁed, rectiﬁed , digitalized, and trans-

ferred to MPU, respectively. At the preliminary stage,

these signals are used to compare which direction is

the strongest one. In near future, we will try to in-

put them into sensing neurons (upper layer) in quasi-

layered RNNM, but in the present study, we must em-

phasize the two points. One is that, the sensing sys-

tem of sound signal from target does not give accu-

rate directional information of target, but rough di-

rectional information of target with uncertainty. The

other is that, these signals inputted from four micro-

phones are not processed with complex techniques

or methods. These are quite important differences

between our work and other conventional robotics.

Now, the problem is how these sensing signals

are sent to the neural chaos simulator, which works

as the neural network system to make adaptive be-

haviors of the robot. In our study, a computer with

good performance is chosen as the neural chaos simu-

lator, which is programmed in C language and works

in Vine Linux. A wireless communication interface

ICFC 2010 - International Conference on Fuzzy Computation

146

Figure 2: The roving robot with sensors including two ultra-

sonic sensors and four microphones: A photo picture (left)

and a sketch map (right).

between the MPU of the robot and the neural chaos

simulator has been built using a pair of Bluetooth

serial adapter and a group of communication proto-

col. After the sensing signals was sent to the neural

chaos simulator, the simulator performs neural infor-

mation processing, produces adaptive motion signals,

and sends them back to the robot again. And then, the

robot moves one step. At a new position, sensing in-

formation from sensors are checked again. The above

process is repeated. Therefore, this is a close-loop

control system. After the sensing systems and com-

munication interface have worked well, it is the key

point whether the neural simulator enables the robot

to produce adaptive motions in various environment,

such as mazes or moving targets. In next section, we

will introduce it in detail.

2.2 Context Setting of Solving Mazes

In the present study, the context setting of solving

mazes is shown as follows.

1) Set a typical ill-posed problem of solving two-

dimensional mazes.

2) Set obstacles unknown by the robot.

3) Set a target emitting a sound signal.

4) Acquire information for reaching the target.

•Check whether obstacles to preventthe robot from

forward moving exist or not, by ultrasonic sensors for

detection.

• Obtain rough direction of the target by four mi-

crophones.

5) Calculate the motion increments at every time

step of updating neural network activity.

3 NEURAL CHAOS SIMULATOR

The neural chaos simulator is utilized to simulate dy-

namical activities of neural network, and works like

the ”brain” of the robot. In various unknown en-

vironment or mazes, chaotic dynamics generated in

the neural network makes the robot generate complex

motions to adapt environment or avoid obstacles. In

our study, we start from a simple RNNM, and de-

velop it to a quasi-layered RNNM so as to approach

the mechanism of brain nearer.

3.1 Recurrent Neural Network Model

Our study works with a fully interconnected RNNM

consisting of N binary neurons, and the updating rule

is deﬁned by

(t + 1) = sgn



∑

j∈G

(r)

(t)



(1)

sgn(u) =



+1 u ≥0;

−1 u < 0.

• S

(t) = ±1(i = 1 ∼N) : the ﬁring state of a neuron

speciﬁed by index i at time t.

• W

: connection weight from the neuron S

to the

neuron S

, W

is taken to be 0.

• r(0 < r < N): fan-in number for neuron S

, named

connectivity

• G

(r): spatial conﬁguration set of connectivity r

for neuron S

At a certain time t, the state of neurons in the network

can be represented as a N-dimensional state vector

S(t), called as state pattern. The updating rule shows

that time developmentof state pattern S(t) depends on

the connection weight matrix W

and connectivity r.

Therefore, when full connectivityr = N−1, by means

of a kind of orthogonalized learning method (Nara

et al., 1995) , appropriately determiningW

could em-

bed a group of N dimensional state pattern as cyclic

memory attractors in N dimensional state space. At-

tractor patterns consists of (K patterns per cycle)× L

cycles, and each patterns has N neurons. For exam-

ple, in Fig.3, we take K = 6, L = 4,and N = 400. In

this case, the ﬁring states of N = 20×20 = 400 neu-

rons are represented by black pixel or white pixel. As

the network evolves with the updating rule for enough

time steps, randomly initial state pattern will converge

into one of embedded cyclic attractors. Now we

Figure 3: One example of embedded attractor patterns:

when connectivity r = N −1, if S(t) is ξ

, then the output

sequence is ξ

, ξ

,..., ξ

, ξ

,....

A NOVEL ADAPTIVE CONTROL VIA SIMPLE RULE(S) USING CHAOTIC DYNAMICS IN A RECURRENT

NEURAL NETWORK MODEL AND ITS HARDWARE IMPLEMENTATION

147

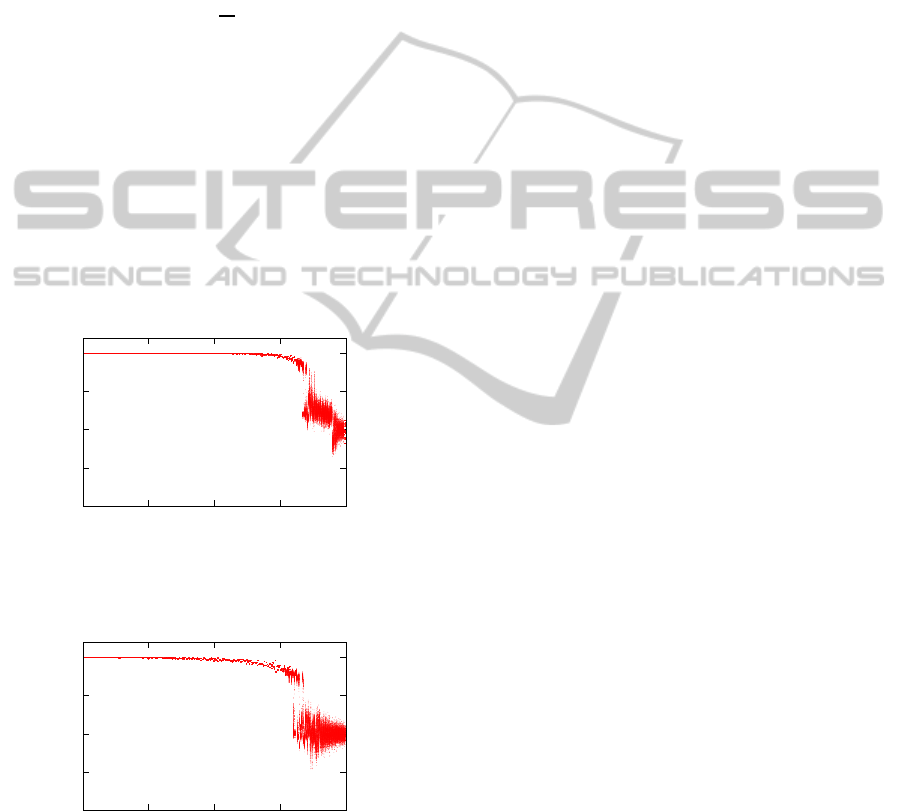
reduce connectivity r by blocking signal transfer from

other neurons, attractors gradually becomes unstable,

and the network state changes from attractor dynam-

ics to chaotic dynamics. In order to analyze the desta-

bilizing process, we have calculated a bifurcation di-

agram of overlap (Fig.4) where overlap means one-

dimensional projection of state pattern S(t) to a cer-

tain reference pattern. Therefore, an overlap m(t) is

deﬁned by

m(t) =

S(0) ·S(t) (2)

t = Kp+ t

(p = 1,2,. . .) (3)

where S(0) is an initial pattern(reference pattern) and

S(t) is the state pattern at time step t. Because m(t) is

a normalized inner product, −1 ≤m(t) ≤ 1. m(t) = 1

means that the present state pattern and the reference

pattern is same. In other words, the reference pattern

repeatedly appears every K=6 steps. In our study, for

the upper layer and the lower layer, we have calcu-

lated the overlap m(t) with respect state pattern S(t)

when it evolves for long time.

-1

-0.5

0.5

0 100 200 300 400

m(t)

Overlap

r(r

u,u

)Connectivity

Figure 4: The long-time behaviours of overlap m(t) at K-

step mappings. The horizontal axis is r(r

u,u

) (0-399).

-1

-0.5

0.5

0 100 200 300 400

l,l

Connectivity

(t)Overlap

Figure 5: The long-time behaviors of overlap m

(t) at K-

step mappings (r

u,l

= 0). The horizontal axis is r

l,l

(0-399).

3.2 Quasi-layered Recurrent Neural

Network Model

A quasi-layered RNNM consists of a upper layer with

N neurons and a lower layer with N neurons. The

upper layer is updated by only self-recurrence. On

the other hand, the lower layer are updated not only

by self-recurrence but also by recurrent outputs of the

upper layer. State pattern S(t) = [x(t),y(t)], where

x(t) = {x

(t) = ±1 | i = 1,2,··· , N} and y(t) =

(t) = ±1 | i = 1, 2,··· ,N}. The updating rules

of two layers are deﬁned by

(t + 1) = sgn



∑

j∈G

)

u−u

(t)



(4)

(t + 1) = sgn



∑

j∈G

)

l−l

(t) +W

u−l

(t)]



,(5)

where u means upper layer, l, lower layer, respec-

tively. W

u−u

is connection weight from neuron x

of upper layer to neuron x

of upper layer, W

u−l

and

l−l

are deﬁned similarly.

In quasi-layered RNNM, if we take sufﬁciently

large connectivity r (r

u,u

≃ N,r

u,l

≃ N,r

l,l

≃ N), by

appropriately determining connection weight W

, a

group of arbitrarily designed state patterns can be em-

bedded as cyclic memory attractors. Certain cyclic

memory attractors are embedded in each layer. Since

three connectivities r

, r

affect the development

of state pattern, for the upper layer and the lower

layer, we have calculated the overlap m(t) with re-

spect state pattern S(t) when it evolves for long time.

The overlap m

(t) of the upper layer as a function of

connectivity r

u,u

is same to Fig.4.

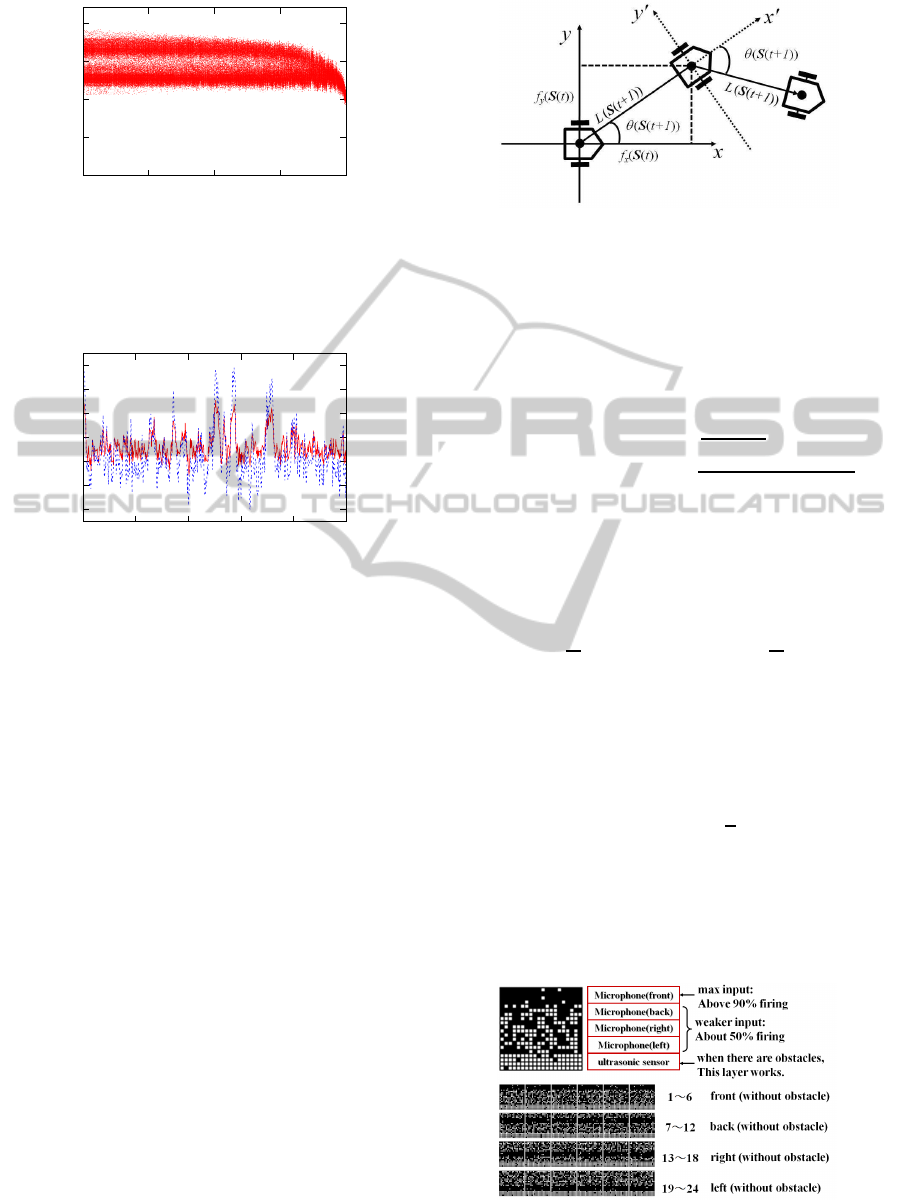
Next, let us show examples about long time be-

haviors of m

(t) for a few cases of connectivities, r

, r

. They are shown in Fig.5 (r

l,l

dependence

when r

u,l

= 0), Fig.6 (r

l,l

+ r

u,l

dependence when

u,l

, 0). About the latter case, let us show an example

of time development of m

(t) and m

(t) in Fig.7 when

u,u

= 40, r

u,l

= 400, r

l,l

= 399, where the lower layer

sensitively responds to the upper layer depending on

what trajectories of the upper layer pass through state

points near the embedded attractors or far from them.

ICFC 2010 - International Conference on Fuzzy Computation

148

-1

-0.5

0.5

0 200 400 600 800

u,l

l,l

Connectivity

(t)Overlap

Figure 6: The long-time behaviors of overlap m

(t) at K-

step mappings (r

u,u

= 40, r

u,l

= 400). The horizontal axis

represents the reduced input connectivity to the lower layer,

0-799.

-0.2

0.2

0.4

0.6

0.8

0 100 200 300 400 500

The number of periodic maping

(t),m

(t)Overlap

Figure 7: The overlap m

(t)(Red solid line) and

(t)(Green broken line) along time axis. The horizontal

axis represents the p-th K-steps, where t = Kp+t

(K = 6

and t

= 1200).

4 DESIGNING ATTRACTORS

FOR CONTROLLING

4.1 Motion Functions

At a certain time t, the robot is assumed to be at

the present origin and orientates 0 (rad), that is, at

any time t, the robot has a local coordinates, which

is shown in Fig.8. Since the robot has two driving

wheels and one castor wheel, when the two driving

wheels rotate with same velocity and reverse direc-

tion, its rotation radius can be regarded as zero if we

do not consider the slippage of the wheels. There-

fore, the motion of the robot at each step includes

two actions. First, the robot rotates with an angle θ(t)

around the present origin. Next, it moves forward for

an distance L(t). In other words, two-dimensional

motions of the robot depend these two time vari-

able θ(t) and L(t). Therefore, in order to realize 2-

dimensional motion of the robot using dynamical be-

havior of the neural network, four hundred dimen-

sional state pattern S(t) is transformed into the rota-

Figure 8: The motion of the robot: at each new position, the

robot has a local coordinates in which x axis always orients

to the front of the robot.

tion angle θ(S(t)) and the moving distance L(S(t)) by

a simple coding, which are called as motion functions

and deﬁned by

θ(S(t)) = tan

−1

(S(t))

(6)

L(S(t)) = πd

(S(t)) + f

(S(t)) (7)

where d is the diameter of the driving wheels, and

(S(t)), f

(S(t)) are the x-axis increment and y-axis

increment in the local coordinates at time t, and are

deﬁned by

(S(t)) =

A·C f

(S(t)) =

B·D (8)

where f

(S(t)) and f

(S(t)) are four N/4 dimen-

sional sub-space vectors of state pattern S(t), which

is shown in Fig.10. The inner products of A·B and

C·D are normalized by 4/N = 100, so f

(S(t)) and

(S(t)) ranges from -1 to +1.Therefore, the rotation

angle θ(S(t)) takes value from −π to π, and the mov-

ing distance L(S(t)), from 0 to

√

2πd.

4.2 Attractors for Controlling

4.2.1 Upper Layer

Figure 9: One of four embedded attractors in upper layer.

A NOVEL ADAPTIVE CONTROL VIA SIMPLE RULE(S) USING CHAOTIC DYNAMICS IN A RECURRENT

NEURAL NETWORK MODEL AND ITS HARDWARE IMPLEMENTATION

149

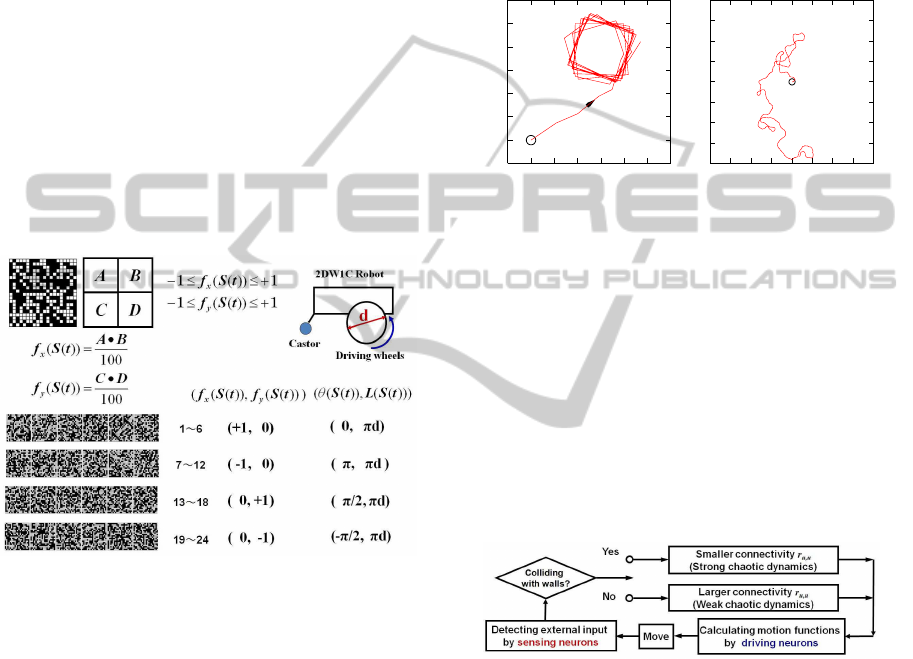
The upper layer for sensing consists of 5 in-

dependent sub-space vectors that corresponds to 5

sensors—four microphones for detecting target direc-

tion and a couple of ultrasonic sensors for detecting

obstacles, shown in Fig.9. Attractors are embedded in

the case that the direction of the maximum signal in-

tensity received by microphones is front, back, right,

or left without obstacles, respectively. As the robot

is moving, the signal intensity of four microphones

changes. Correspondingly,ﬁring state of sensing neu-

rons in the upper layer sensitively responds to exter-

nal signal input and produce adaptive dynamics to act

driving neurons. On the other hand, if there are obsta-

cles to prevent the robot from moving forward, sens-

ing neurons corresponding to ultrasonic sensors are

activated, and cause strong chaotic dynamics in sens-

ing neurons to act driving neurons so as to enable the

robot to perform complex motions.

4.2.2 Lower Layer

Figure 10: Attractor patterns designed for motion control:

Each cyclic memory corresponds to a prototypical simple

motion.

The lower layer for driving consists of four groups

of attractor patterns, shown in Fig.10. Each attrac-

tor pattern consists of four random sub-space vectors

A,B,C and D. A and B are independent random pat-

terns. A group of speciﬁed intra-pattern structure is

given, such as A = C or −C and B = D or −D in the

present study. By the coding of motion functions,

each group of attractor pattern corresponds to one of

stationary motions in two-dimensional space.

5 CONTROL ALGORITHM

The study on RNNM tells that sufﬁciently large or

quite small connectivity r enables the neural network

to generate chaotic dynamics or attractor dynamics

(Nara and Davis, 1992). In quasi-layered RNNM, a

group of connectivity (r

u,u

, r

u,l

, r

l,l

) should be con-

sidered. Here, when r

l,l

is set as 60, and different

u,u

causes chaotic dynamics with different dynam-

ical properties. Correspondingly, by the coding of

motion functions, the robot shows weak (localized)

chaotic motions ( Fig.11(left)), or strong chaotic mo-

tions ( Fig.11(right)). On the other hand, by virtue

-0.1

0.1

0.2

0.3

0.4

0.5

0.6

-0.1 0 0.1 0.2 0.3 0.4 0.5 0.6

START

-8

-6

-4

-2

-8 -6 -4 -2 0 2 4 6 8

START

Figure 11: Examples of motion control (r

u,l

= 400 and

l,l

= 60): (left) larger r

u,u

= 60 generates weak chaotic

dynamics with localized property, (right) smaller r

u,u

= 20

causes strong chaotic dynamics.

of the sensitivity of chaos in quasi-RNNM, once the

best optimized connectivities are appropriately de-

termined, it will work well even when obstacle in-

formation is given to sensing neurons. However, at

the present stage, only rough target directional in-

formation is given to sensing neurons, and adaptive

switching of connectivity r

u,u

is utilized to control the

robot in two-dimensional mazes. The control algo-

rithm is shown in Fig.12. Depending on the sound

Figure 12: Control algorithm of solving 2-dimensional

mazes.

signal intensity from the target caught by four micro-

phones, sensing neurons in the upper layer sensitively

response it. Correspondingly, driving neurons in the

lower layer sensitively responds to sensing neurons

and the robot adaptively turn toward the strongest in-

tensity direction quickly due to sensitivity of chaotic

dynamics. When there are no obstacles in the range

of ultrasonic sensor, the robot moves with larger con-

nectivity r

u,u

. When there is an obstacle, it moves

chaotically with smaller connectivity r

u,u

and trys to

ﬁnd detour to avoid obstacles. Several examples of

computer experiment are shown in Fig.13. In near fu-

ture, switching of connectivity r

u,u

will be replaced

ICFC 2010 - International Conference on Fuzzy Computation

150

with only sensing neurons responding to external in-

put adaptively.

-1

-1 0 1 2 3 4 5 6

START

TARGET

-1

-1 0 1 2 3 4 5 6

START

TARGET

WALL

(a) (b)

Figure 13: Examples of Computer simulation: (a) No obsta-

cle, r

stays at larger one; (b) When obstacles prevent the

robot from moving forward, smaller r

is used to update

the network.

6 EXPERIMENT OF HARDWARE

IMPLEMENTATION

In the present experiment, a loud speaker is set as a

target, which is emitting a speciﬁed sound signal like

calling song of a male cricket. When the robot is mov-

ing like a female cricket in two-dimensional space,

it can catch only rough directional information from

four microphones, which are attached to the front,

the back, the left and the right of the robot. Accord-

ing to the control algorithm shown in Fig.12, several

kinds of typical 2-dimensional mazes have been con-

structed. Using chaotic dynamics, the robot success-

fully avoids obstacles and reaches the target. Fig.14

shows some video snapshots of the robot solving the

above 2-dimensional maze. Now we are devoting our-

self to implement sensing neurons into the robot, and

will report them in near future.

(a) t = 0s (b) t = 408s

Figure 14: Video snapshots of the roving robot walking on a

horizontal ﬂoor where there are obstacles between the robot

and the target. Around the starting point, because the dis-

tance is a little far from the target, the robot shows chaotic

motion (a), chaotically walks for ﬁnding appropriate detour

and reaches the target (b).

7 DEVELOPING HARDWARE

IMPLEMENTATION & DEVICE

FABRICATION

Now, we brieﬂy show our preliminary results about

the further developments based on our idea to use

functional chaos.

7.1 A Roving Humanoid Robot and an

Arm Robot Driven by Chaos

Based on our idea, we show the other examples.

One is the case that the same method of solving 2-

dimensional mazes is applied to a humanoid robot

with two legs as shown in Fig.15. This experiment is

desinged to develope our idea to 3-dimensional con-

ﬁguration of obstacles, whereas the previous example

is to solve 2-dimensional mazes. Thus, the behaviors

necessarily include the actions not only of straddling

or to step over obstacles but also of climbing up and

down obstacles, if they would have appropriate sizes

(see Fig.16). This experment is still under going.

Figure 15: A humanoid robot used in our experiment.

The other experiment is to apply the same idea

to arm motions of animals like humanbeings or mon-

keys. However, it should be noted that we set the sit-

uation in which the robot does not have advanced vi-

sual information processing ability like manmals but

has only poor visual sensing system. The set situation

is that the sensors can detect only rough direction of

target with including uncertainty. The four infrared

light sensors are attached on the arms to realize such

ill-posed situations. (see Fig.17) At present, the ex-

periment succeed only in the case without obstacles.

(see Fig.18).

A NOVEL ADAPTIVE CONTROL VIA SIMPLE RULE(S) USING CHAOTIC DYNAMICS IN A RECURRENT

NEURAL NETWORK MODEL AND ITS HARDWARE IMPLEMENTATION

151

Figure 16: A humanoid robot under the action of climbing

upstairs.

Figure 17: An arm robot used in our experiment.

Figure 18: An arm robot under the action of reaching the

target.

7.2 A Pseudo-neuron Device and a

Diffusively Coupled Network of

them

In this section, we report our study about pseudo-

neuron device fabricated by Self Electro-optic Ef-

fect Device (SEED) and coupled dynamic SEED (D-

SEED).

7.2.1 Self Electro-optic Effect Device (SEED) &

Dynamic SEED

A typical single SEED composed of p-i-n semicon-

ductors is shown in Fig. 19. The primary variable

of this system is photocarrier density n which is gen-

erated by the incident optical power P

, where the

rate equation for photocarrier density n is given later.

The important point is that it indicates a bistable prop-

erty with respect to incident optical power as shown

in Fig.20.

Figure 19: Single SEED.

Input Power [mW]

Photocarrier Density [

×10

-3

]

0 0.2 0.4 0.6

0.25

0.5

Stable

Unstable

Figure 20: Bistability.

Now let us propose a pseudo-neuron device that

consists of two bistable SEED elements optically con-

nected in a series with feedback from one of them to

the power of an incident light beam (Fig. 21). We

called it ”Dynamic SEED (D-SEED)”.

Figure 21: Serially connected SEEDs with feedback.

Coupled rate equations for photocarrier density n

(upper) and n

(lower) are represented as

= −

+ P

)Ω

{ω−ξ

}



Ω



(9)

= −

+ P

−m

)Ω

{ω−ξ

}



Ω



(10)

= ω

−β(V

−R

) (i = 1,2) (11)

= AI

(12)

where τ, α, Ω

, ω, ω

, β, V

, V

, R, η are system pa-

rameter. Note that the primary parameter is P

which

ICFC 2010 - International Conference on Fuzzy Computation

152

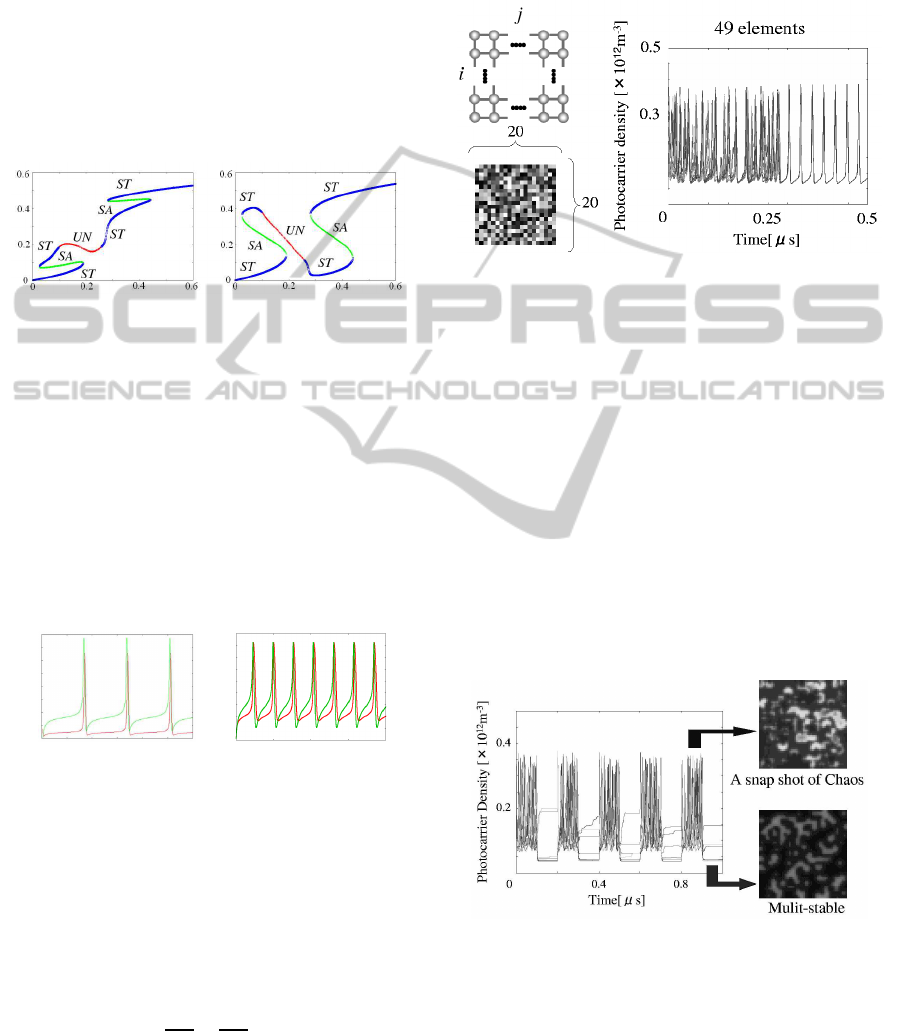
causes many kind of bifurcation phenomena. m is ab-

sorption parameter and A is feedback gain parameter.

The rate equations show that for the upper SEED

feedback light is added to incident light, whereas the

lower SEED received the light decreased by the ab-

sorption in upper SEED. When we choose appropri-

ate parameter values, we can obtain various bifurca-

tion phenomena as shown in Fig. 22. Important bi-

furcations are ”Hopf bifurcation” and ”Saddle-node

bifurcation”.(Ohkawa et al., 2005)

Input Power [mW] Input Power [mW]

Photocarrier Density [

×10

-3

]

Photocarrier Density [

×10

-3

]

Figure 22: Stationary solutions of upper SEED (left) and

lower SEED (right) as a fuction of input light power P

Blue lines, green lines and red lines indicate stable ”ST”,

saddle ”SD” and unstable ”UN” respectively.

The important point of this case is that a saddle-

node bifurcation occurred on the marginal limit cy-

cle, so that, period of limit cycle becomes inﬁnitely

long as light power approaches the saddle-node bifur-

cation point (Fig. 23). Two typical cases of oscillation

are shown in Fig. 23. Now we extend our idea to a

0.20.1

0.2

0.4

Photocarrier Density [×10

-3

]

Time[μs]

0.20.10

0.2

0.4

Photocarrier Density [×10

-3

]

Time[μs]

0.05

0.3

upper

lower

Figure 23: Oscillatory solutions of n

and n

for input light

power, P

= 0.170 (left), 0.220 (right), respectively. Note

that periods become inﬁtely long as they approach edges

of saddle-node bifurcation points around unstable regions

(Fig. 22).

network of D-SEEDs which are diffusively coupled

in two-dimentional array. Coupled rate equations are

written include diffusion term from Eq. (13).



∂

∂x

∂

∂y



 D(n

i−1, j

+ n

i+1, j

+ n

i, j−1

+ n

i, j+1

−4n

i, j

) (13)

Where (i, j) means the position of D-SEEDs in ar-

rays located in lattice points in two-dimensions, as

shown in Fig. 24 (left-up). Under cetain light power,

time-dependence of carrier density shows chaotic dy-

namics and long time behavior converge into syn-

chronaized periodic oscillation (Fig. 24 (right)). We

Figure 24: Two-dimensional square lattice D-SEEDs (left-

up), snapshot of a network state at a certain time step, where

brightness of each cell corresponds to n

i, j

and is represented

in grayscale normalized by maximum value of carrier den-

sity (left-low), and Example of time-dependence carrier

density (chaotic oscillation).

conﬁrmed it in the numerical simulation for vari-

ous initial conditions. We obtained global spatio-

temporal chaotic dynamics if we sufﬁciently increase

the number of D-SEEDs. By varying light power,

we also conﬁrmed multi-stable state. In Fig. 25,

we succeeded to obtain switching between two states,

chaotic state and multi-stable state, by varying inci-

dent light power. Now we try to apply chaos to a novel

control by adaptive switching among chaotic state,

multi-stable state and synchronized periodic state.

Figure 25: Switching between two states by varying light

power and P

=0.160 (Chaos) and 0.110 (Multi-stable).

7.2.2 Complex Control using Pulsed Neuron

Network

In our previous studies, The key idea is adaptive

switching between chaotic dynamics and atractor dy-

namics. Now, it is necessary to develop hardware

A NOVEL ADAPTIVE CONTROL VIA SIMPLE RULE(S) USING CHAOTIC DYNAMICS IN A RECURRENT

NEURAL NETWORK MODEL AND ITS HARDWARE IMPLEMENTATION

153

implementation of artiﬁcial neuron device. As func-

tional examples, let us pick up two cases. One is ap-

plication to motion control and the other is to mem-

ory dynamics using D-SEEDs network (pulsed neu-

ron network). In this paper, only the former is de-

scribed.

Now let us consider to solve two-dimensional

maze as an example of ill-posed problems as shown

in the previous sections. We attempt to solve maze

by adaptive switching between chaotic dynamics and

atractor dynamics with D-SEEDs network. State pat-

tern of the network is represented by 400-dimensional

state vectors, while motion in 2-dimensional space

is only two-dimensional vectors. Therefore, it is

necessary to convert 400-dimensional state to 2-

dimensional motion by coding function. We designed

3 different coding methods to prove effectiveness of

chaos which is caused various methods. Our coding

methods are introduced as follows.

(a) Adaptive switching between chaotic state and

synchronized periodic state.

(b) Adaptive switching between chaotic state and

multi-stable state.

Let us consider these two cases. We calculate 2-

dimensional motion(Fig.26) from 400-dimensional

state by coding function.

Figure 26: 2-dimensional motion.

In the coding method (a), we introduce the cod-

ing but let us discard their detailed description. Next,

coding

0.5

object

Figure 27: Coding method (b)-1.

in the coding method (b), let us propose the two cod-

ing methods. One is shown in Fig.27, and the other

is shown in Fig.28, where the detailed deﬁnition of

motion increments are discarded as well.

Figure 28: Coding method (b)-2.

So it is possible to obtain 4 monotonic motions

which are almost linear motions to 4 quadrants di-

rection and chaotic motion by changing the position.

Now, we solve maze by adaptive switching between

monotonic motion and chaotic motion with a simple

control algorithm shown in Fig. 29. We assume that,

1. An object can acquire only rough direction in

which quadrant it exists.

2. The object does not have pre-knowledgeaboutob-

stacle conﬁgulation.

These context settings give an ill-posed problem.

According to the control algorithm shown in Fig. 29.

Direction of movement

Direction to target

＝

Direction of movement

Direction to target

＝

Direction of movement

Direction to target

＝

Monotonic motion (multi-stable)

YES

Chaotic motion (chaos)

The obstacle exists

in direction of movement

YES

Move

Figure 29: Control algorithm of adaptive switching between

chaotic motion and monotonic motion.

The successful results of computer experiments were

obtained and will be reported in the conference and in

a recent paper as well.

8 CONCLUDING REMARKS

Even from the results of the present preliminary ex-

periment, we can conclude that chaotic dynamics is

useful to solve complex problems, such as mazes, not

only in computer experiments, but also in hardware

implementation of the robot systems. Although detail

consideration should be done from functional aspects,

it is at least an evidence that chaotic dynamics could

play important roles in biological systems including

brain. Therefore, we are sure that those novel func-

tional aspects of chaotic dynamics could be applied to

complex control by simple rule in systems with large

but ﬁnite degrees, and be useful to engineering ap-

plication mimicking excellent functions observed in

biological systems including brain.

ICFC 2010 - International Conference on Fuzzy Computation

154

ACKNOWLEDGEMENTS

This work has been supported by Grants-in-Aid for

Scientiﬁc Research, #19500191 in Japan Society for

the Promotion of Science and #22120509 in the Min-

istry of Education, Culture, Sports, Science & Tech-

nology.

REFERENCES

Fujii, H., Itoh, H., Aihara, K., Ichinose, N., and Tsukada,

M. (1996). Dynamical cell assembly hypothesis-

theoretical possibility of spatio-temporal coding in the

cortex. In Neural Networks. vol. 9, p. 1303.

Huber, F. and Thorson, H. (1985). Cricket auditory com-

munication. In Sci. Amer. vol. 253, pp. 60-68.

Li, Y. and Nara, S. (2008). Novel tracking function of mov-

ing target using chaotic dynamics in a recurrent neural

network model. In Cognitive Neurodynamics. vol. 2,

pp. 39 - 48.

Mikami, S. and Nara, S. (2003). Dynamical responses of

chaotic memory dynamics to weak input in a recurrent

neural network model. In Neural Computing. vol. 11,

pp. 129-136.

Nara, S. (2003). Can potentially useful dynamics to solve

complex problems emerge from constrained chaos

and/or chaotic itinerancy? In Chaos. vol. 13, pp.

1110-1121.

Nara, S. and Davis, P. (1992). Chaotic wandering and search

in a cycle memory neural network. In Progress of The-

oretical Physics. vol. 88, pp. 845-855.

Nara, S., Davis, P., Kawachi, M., and Totuji, H. (1993).

Memory search using complex dynamics in a recur-

rent neural network model. In Neural Networks. vol.

6, pp. 963-973.

Nara, S., Davis, P., Kawachi, M., and Totuji, H. (1995).

Chaotic memory dynamics in a recurrent neural net-

work with cycle memories embedded by pseudo-

inverse method. In Int. J. Bifurcation and Chaos Appl.

Sci. Eng. vol. 5, pp. 1205-1212.

Ohkawa, Y., Yamamoto, T., Nagaya, T., and Nara, S.

(2005). Dynamic behaviors of coulpled self-electro-

optic effec devices. In Appl. Phys. Lett. vol. 86, p.

111107.

Skarda, C. A. and Freeman, W. J. (1987). How brains make

chaos in order to make sense of the world. In Behav-

ioral and Brain Sciences. vol. 10, pp. 161-195.

Suemitsu, Y. and Nara, S. (2004). A solution for two-

dimensional mazes with use of chaotic dynamics in

a recurrent neural network model. In Neural Compu-

tation. vol. 16, pp. 1943-1957.

Tokuda, I., Nagashima, T., and Aihara, K. (1997). Global

bifurcation structure of chaotic neural networks and its

application to traveling salesman problems. In Neural

Networks. vol. 10, pp. 1673-1690.

Tsuda, I. (2001). Towards an interpretaion of dynamic neu-

ral activity in terms of chaotic dynamical systems. In

Behavioral and Brain Sciences. vol. 24, pp. 793-847.

A NOVEL ADAPTIVE CONTROL VIA SIMPLE RULE(S) USING CHAOTIC DYNAMICS IN A RECURRENT

NEURAL NETWORK MODEL AND ITS HARDWARE IMPLEMENTATION

155