TRADINNOVA-FUZ: FUZZY PORTFOLIO INVESTMENT

Dynamic Stock Portfolio Decision-making Assistance Model

based on a Fuzzy Inference System

Isidoro J. Casanova

Department of Informatics and Systems, University of Murcia, Campus de Espinardo, 30100 Murcia, Spain

Keywords:

Finance, Portfolio selection, Trading system, Decision support system, Fuzzy inference system.

Abstract:

This paper describes a decision system based on rules for the management of a stock portfolio using a fuzzy

inference system to select the stocks to be incorporated. This system simulates the intelligent behavior of an

investor, carrying out the buying and selling of stocks, such that during each day the best stocks will be selected

to be incorporated in the portfolio with the use of technical indicators using a fuzzy logic based approach. The

proposed novel fuzzy system only has a simple strict set of rules to decide if a share is bought or not, unlike

other systems that also include rules for the sale and have a lot of complicated rules.

The system has been tested in 3 time periods (1 year, 3 years and 5 years), simulating the purchase/sale of

stocks in the Spanish continuous market and the results have been compared with the revaluations obtained by

the best investment funds operating in Spain.

1 INTRODUCTION

Investment management consists of strategic asset al-

location, tactical asset allocation, and stock picking

three phases (Amenc and Sourd, 2003). Our study is

focus on tactical asset allocation and stock picking.

To perform the tactical asset allocation an intelli-

gent system based on rules that will dynamically in-

vest in shares for a certain period of time is proposed.

This system will simulate the behavior of any rational

investor, so that each day would look if there is any

investment opportunity, buying or not depending on

how much money is available.

The last phase, stock picking, is one of the most

important phases, since it must decide for each day

what shares should be bought to add to the portfo-

lio. A simple rule that could be used to implement

this step could be to invest in the stock that has been

revalued at least a certain percentage in the last days.

Although we could use more sophisticated rules using

technical analysis, like Relative Strength Index (RSI)

or Moving Average, (Murphy, 1999).

Each of the indicators used in technical analysis

has some limitation, and in most cases, the answer

by each of them is not a deﬁnite “yes” or “no”. The

best result could be achieved when combining many

indicators at the same time and evaluating their output

collectively.

Our proposal is to use technical indicators with

fuzzy logic in order to create a strict fuzzy indicator

that only recommends “buy”, when most of the tech-

nical indicators recommend it.

The proposed system will be applied to the Span-

ish stock market, in particular, the IBEX 35

, keep-

ing in mind that we invest all the available money

in stocks without regard to which sector they belong,

and supporting a maximum of 4 % loss per share. We

will compare our investment performance with the in-

dex itself and with the results that have obtained the

better equity funds that invest in the Spanish continu-

ous market in the time limit of 1, 3 and 5 years.

In Section 2, we introduce the concepts of invest-

ment portfolio and how fuzzy inference systems have

been introduced in order to help in ﬁnancial market

analysis. In Section 3, we present the system pro-

posed with all the elements that compose it. In Sec-

tion 4, we show different computational results that

illustrate the behavior of the proposed hybrid intelli-

gent system. Finally, we present the conclusions in

Section 5.

The IBEX 35 (an acronym of Iberia Index) is the

benchmark stock market index of the Bolsa de Madrid,

Spain’s principal stock exchange.

J. Casanova I..

TRADINNOVA-FUZ: FUZZY PORTFOLIO INVESTMENT - Dynamic Stock Portfolio Decision-making Assistance Model based on a Fuzzy Inference

System.

DOI: 10.5220/0003058400670072

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICFC-2010), pages

67-72

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

2 LITERATURE REVIEW

2.1 Investment Portfolio

The concept behind investment portfolio is to com-

bine different investment targets to avoid concentrat-

ing too much risk on any one target with the aim of

dispersing overall investment risk. Any combination

of two or more securities or assets can be termed an

investment portfolio.

On the other hand efﬁcient-markethypothesis is an

idea partly developed in the 1960s by Eugene Fama

and defended by Burton G. Malkiel (Malkiel, 1973)

which asserts that ﬁnancial markets are “information-

ally efﬁcient”, or that prices on traded assets (e.g.,

stocks, bonds, or property) already reﬂect all known

information, and instantly change to reﬂect new in-

formation. Therefore, according to theory, it is im-

possible to consistently outperform the market by us-

ing any information that the market already knows,

except through luck.

2.2 Fuzzy Inference Systems

A fuzzy inference system is a computer paradigm

based on fuzzy set theory, fuzzy if-then-rules and

fuzzy reasoning.

Fuzzy inference systems have been successfully

applied in ﬁelds such as automatic control, data clas-

siﬁcation, decision analysis, expert systems, and com-

puter vision. Because of its multidisciplinary nature,

fuzzy inference systems are associated with a number

of names, such as fuzzy-rule-basedsystems, fuzzy ex-

pert systems, fuzzy modeling, fuzzy associative mem-

ory, fuzzy logic controllers, and simply (and ambigu-

ously) fuzzy systems.

In the ﬁeld of ﬁnancial market analysis, we have

for example, (Dourra and Siy, 2002), which uses

three technical indicators (rate of change, stochastic

momentum and resistance indicator) in a fuzzy con-

trol system with the following modules: convergence

(maps the technical indicators into new inputs), fuzzi-

ﬁcation, fuzzy processing and defuzziﬁcation (using

the center of area method to map the output universe

with four membership functions -low, medium, big

and large- into a nonfuzzy action). Also in (Che-

ung and Kaymak, 2007) the fuzzy trading system

is based on four technical indicators (Moving Av-

erage Convergence/Divergence, Commodity Channel

Index, Relative Strength Index and Bollinger Bands)

and the output of the fuzzy system is a signal on a nor-

malized domain, on which four different fuzzy sets

(strong sell, sell, buy and strong buy) are deﬁned.

On the other hand in (Atsalakis and Valavanis,

2009) use a neuro-fuzzy based methodology to fore-

cast the next day’s trend of chosen stocks. The fore-

casting is based on the rate of change of three-day

stock price moving average.

3 RESEARCH FRAMEWORK

3.1 Intelligent System for Tactical Asset

Allocation

The proposed system for decision making is based on

a policy of buying and selling the stocks that make up

any stock market over a period of time.

This policy of buying and selling is based on that

if we assume a stock market quoted from a start date

(date

start

) until an end date (date

end

), each one of

those days, all their stocks have had an opening price

open

), a maximum price (p

max

), a minimum price

min

) and a closing price (p

If we take a day d between date

start

and date

end

which you have no shares purchased (there is no order

of sale or purchase pending), then we will be able to

select a set of m stocks (S

), using technical analysis

or any other technique, which would be most recom-

mendable to buy, because it expects them to give a

good return.

The technique for selecting stocks should calcu-

late a value for each one of the stocks that make up the

market on that day d, quantifying if it would be advis-

able to buy the shares. Stocks are ordered from most

to least according to this value, and the system will

have to choose the best set of stocks, deﬁning which

minimum value is considered for a stock to belong

to this set of the better stocks, existing the possibility

that one day any stock is not recommended (m = 0),

or that many are recommended because its analysis

has been the sufﬁciently satisfactory for all them.

Once we have this set S

with the selection of the

best stocks for a day d, we might try to buy all or some

of these stocks. To simplify the algorithm we will try

to buy only one of the selected stocks every day, so

that after several days, we could have a portfolio of

n stocks (S

). Thus, to choose the stock to buy we

would have two possibilities, to select the best or well

to select any randomly.

Once we have chosen a stock, we will have to give

the purchase order for the next day. We will limit the

purchase price to any of the prices that has had the

stock during that same day ([p

min

, p

max

]), or choose

the opening p

open

or closing p

price of the next

day. If we use a low purchase price, there are fewer

ICFC 2010 - International Conference on Fuzzy Computation

possibilities to execute the purchase in the following

days, but on the other hand, the stock will be bought

more cheaply.

The next day (d + 1), one sees if the purchase

of the share can be executed, whenever the purchase

price of this day is between p

min

and p

max

. If this

purchase order does not manage to be executed in

W days, then we would eliminate this purchase or-

der, and would give a new purchase order, selecting a

share among the best ones of that day. On this follow-

ing day in which we can already have bought shares, it

is necessary to calculate which of them should be kept

in the portfolio and which should be sold, reason why

a new analysis is performed to select p stocks (S

) so

that using again anyone of the previously commented

techniques would tell us which stocks shall be main-

tained in the portfolio, since it is expected that they

give a good proﬁt value. The technique used must

calculate a value for each of the stocks that make up

the market on that day d + 1, quantifying if it would

be advisable to maintain this share in the portfolio.

In this new day we would check if each one of

the bought stocks continues being among the best that

are recommended to maintain in the portfolio (S

), in

which case we would not do anything or otherwise we

would leave spent M days without the stock among

the best to give a sale order. A sale order is given

when M days have passed without the stock is recom-

mended to keep in the portfolio or when the stock has

had a loss regarding the price of purchase higher than

a certain percentage P%. A sale order will also have

a limited price, as the purchase order. The higher the

sale price more difﬁcult it is to execute the sell or-

der. In case during V days it is not possible to sell at

this price, probably because the stock is in a bearish

period, then we would descend the price of this sale

order.

3.2 Stock Picking based on a Fuzzy

Inference System

For every day d along the investment period it is nec-

essary to look for which are the best shares S

to be

able to introduce them in the decision support sys-

tem dedicated to tactical asset allocation commented

in the previous paragraph, and that this one decides

how it is going to invest in them.

To select the best shares of one day d, we are go-

ing to use technical analysis indicators, although the

most difﬁcult part of technical analysis is to decide

which indicator to use.

We have chosen the following four technical indi-

cators to select stocks:

1. Average Revaluation Period (ARP). Average

revaluation that has had a stock in a given period

of time.

2. Relative Strength Index (RSI). Relative

Strength Index of a stock in a given period of

time.

3. Moving Average (MA). Calculates the revalua-

tion that reaches a stock with respect to the aver-

age value of price in a given period of time.

4. Double Moving Average (DMA). Known also as

double crossover method, uses a combination of

long-term and short-term moving averages. When

the shorter moving average rises above the longer

moving average from below, a buy signal is is-

sued.

The results of applying these indicators to the

stocks are going to be the input variables in the fuzzy

inference system. We have chosen these indicators

because they are basic in the world of technical anal-

ysis, and because they are very easy to understand.

Technical analysis deals with probability and

therefore multiple indicators can be used to improve

the result. In most cases, the answer by each indicator

is not a deﬁnite yes or no answer.

We are going to use technical indicators with

fuzzy logic to create a strict fuzzy indicator that only

recommends to buy a stock when the set of indicators

does it. We will only focus on the purchase recom-

mendations, because the intelligent system discussed

in the preceding section will be in chargeof managing

the portfolio, selling those shares no longer necessary.

Our plan can be summarized as follows:

• To create membership functions, where the inputs

are each one of the ﬁnancial indicators and the

outputs are these indicators “fuzziﬁed”

• To create fuzzy rules that indicate if it is highly

recommendable to buy a share.

• To translate the fuzzy output into a crisp trading

recommendation.

3.2.1 Fuzziﬁcation

The input variables in this fuzzy inference system are

mapped by sets of membership functions, known as

“fuzzy sets”. The process of converting a crisp input

value to a fuzzy real value between 0 and 1 is called

“fuzziﬁcation”. The fuzziﬁcation comprises the pro-

cess of transforming crisp values into grades of mem-

bership for linguistic terms of fuzzy sets. The mem-

bership function is used to associate a grade to each

linguistic term.

Our fuzzy system also have a “ON-OFF” type of

switch for the Double Moving Average input vari-

able, because this input will always have a truth value

TRADINNOVA-FUZ: FUZZY PORTFOLIO INVESTMENT - Dynamic Stock Portfolio Decision-making Assistance

Model based on a Fuzzy Inference System

equal to either 1 or 0, depending if the buy signal has

been issued.

There is yet no ﬁxed, unique, and universal rule

or criterion for selecting a membership function for

a particular “fuzzy subset” in general: a correct and

good membership function is determined by the user

based on his scientiﬁc knowledge, working experi-

ence, and actual need for the particular application in

question.

The criteria followed in the fuzziﬁcation of prof-

itability and RSI are explained below.

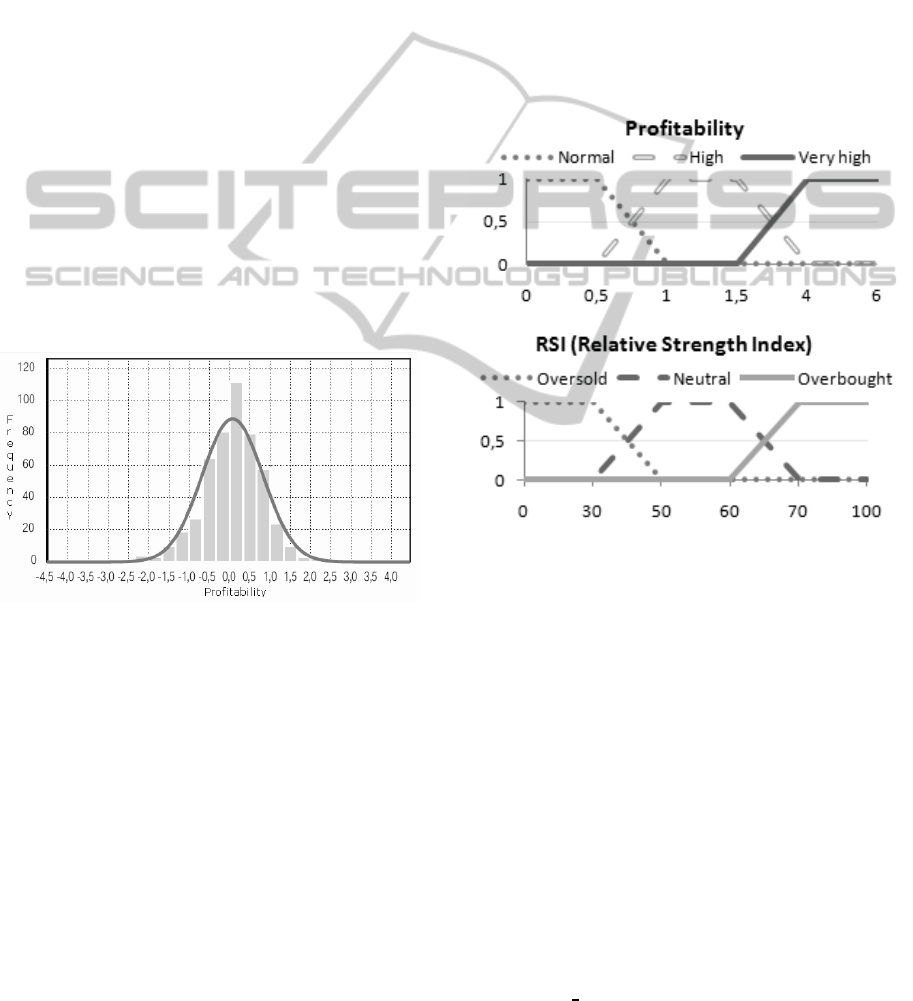
Fuzziﬁcation of Proﬁtability. At the moment of

carrying out the fuzziﬁcation of the daily proﬁt val-

ues, the present fuzzy systems usually assign “low”,

“normal” or “high” proﬁtability values according to

subjective estimations carried out by the writer of the

article.

In this research, in order to perform this fuzzy-

ﬁcation we need to keep in mind that, statistically

(Figure 1), is considered normal proﬁtability between

0% and 0.5%-1%, high proﬁtability between 0.5%-

1% and 1.5%-4%, and very high proﬁtability from

1.5%-4%, (BME, 2009).

Figure 1: Histogram of daily returns on IBEX35 (2003-

2005).

The membership grade functions deﬁned on the

proﬁtability domain are based on trapezoid shapes

(Figure 2). It can be seen that just positive returns

have been considered, since only this type of proﬁt

values will be able to originate recommendations for

purchase.

Fuzziﬁcation of RSI. The Relative Strength Index

(RSI) method, which was developed by J. Welles

Wilder, may be classiﬁed as a momentum oscillator,

measuring the velocity and magnitude of directional

price movements. Momentum is the rate of the rise or

fall in price.

Wilder posited that when price moves up very

rapidly, at some point it is considered overbought.

Likewise, when price falls very rapidly, at some point

it is considered oversold. In either case, Wilder felt a

reaction or reversal is imminent.

As a result, Wilder believed that tops and bottoms

are indicated when RSI goes above 70 or drops below

30. Traditionally, RSI readings greater than the 70

level are considered to be in overbought territory, and

RSI readings lower than the 30 level are considered

to be in oversold territory. In between the 30 and 70

level is considered neutral.

The membership grade functions deﬁned on the

RSI domain (Figure 2) have the following fuzzy sets

(overbought, oversold and neutral) based on a trape-

zoid shape.

Figure 2: Membership functions.

3.2.2 Fuzzy Rule Base

Decisions are made based on fuzzy rules. These rules

are characterized by a collection of fuzzy IF THEN

rules in which the preconditions and post-conditions

involve linguistic variables. This collection of fuzzy

rules characterizes the behavior of the system in a lin-

guistic form that is close to the way human think.

Designing a good fuzzy logic rule base is key to

obtaining a satisfactory controller for a particular ap-

plication. Therefore, when designing the rules, it has

been taken into account that only those rules that de-

ﬁne the purchase of a stock must be deﬁned, and they

should be the easiest possible rules so as to under-

stand its application. Thus, only the linguistic term

associated with the most representative membership

function to make a purchase (“RSI oversold” or “prof-

itability very high”) has been used when setting these

rules, and not other membership functions such as

ICFC 2010 - International Conference on Fuzzy Computation

“proﬁtability high” which are usually used in other

researches.

For simplicity of design we have taken linear

input-output relations (implications) in a SISO sys-

tem. Generally, in multiple-input/multiple-output

(MIMO) fuzzy inference systems, it is difﬁcult to gen-

erate control rules.

Keeping the rules mentioned above in mind, the

rules that we have deﬁned are the following:

1. IF RSI is oversold THEN buy

2. IF DMA is buy signal THEN buy

3. IF MA is very high THEN buy

4. IF ARP is very high THEN buy

5. OTHERWISE not buy

The antecedent (the rules premise) describes to

what degree the rule applies, while the conclusion (the

rules consequent) assigns a membership function to

the output variable.

The output variable “buy” is assigned a range be-

tween 0 and 1. A low value represents that is not a

good idea to buy the stock and a high value represents

an excellent opportunity to buy the stock. There is

an inverse relationship between the output member-

ship functions “buy” and “not buy” so that: buy = 1 -

not buy.

The strength of the ith fuzzy rule is calculated by

evaluating the strength of the precondition i (degree

of truth) on the corresponding output membership.

The ﬁnal value of the output variable will correspond

exactly with the value that reaches the membership

function in the precondition.

3.2.3 Combining Rules and Defuzziﬁcation

As all the rules are activated every day resulting in

different values for the output fuzzy set “buy”, cor-

responding each output value with the value of the

fuzziﬁed input, we are going to perform a combi-

nation of rules additive, (Kosko, 1992), to obtain a

unique ﬁnal value assigning a weight to each rule.

The weight of the combiner can be thought of as

providing degrees of belief to each rule, but we con-

sider that all the rules have the same importance, so

we set all the weights equal to unity.

Defuzzication is a mapping process from a fuzzy

space deﬁned over an output universe of discourse

into a nonfuzzy (crisp) action. It is not a unique oper-

ation as different approaches are possible.

The ﬁnal output of the system (a crisp control sig-

nal) is a value between 0 and 1. A strong buy signal is

generated when the output is close to 1.0 and a strong

not buy signal is generated when the output is close to

zero.

The fuzzy logic and the fuzzy control rules are

considered and are chosen so that the defuzziﬁed out-

put is always a linear function of the inputs to the

fuzzy controller. According to (Sun and Liu, 2002)

the output of multiple input single output fuzzy logic

controller can be represented by the convex linear

combination of the inputs of fuzzy logic controller.

Therefore, to calculate the ﬁnal output of the sys-

tem we calculate the average of the fuzziﬁed values

that have been returned by the selected membership

functions.

4 EXPERIMENTS AND RESULTS

We are going to verify the operation of the system

in 3 periods of time: 5 years (2005-2009), 3 years

(2007-2009) and 1 year (2009). The market where

we will operate will be the Spanish stock market, but

restricted to the shares that conformed the IBEX35 in

the year 2009. The historic prices have been corrected

of dividends, splits and increases in capital. The short

selling is not allowed. The cost of each trade has been

taken into consideration, so that we assume that the

ﬁnancial intermediary charges a fee of 0.2% and we

are going to consider the transaction fees published

by the market of Madrid.

The portfolio will be formed by 14 shares as max-

imum and the rule which is responsible for deﬁning

whether a stock should remain in the portfolio has

been deﬁned so that the Relative Strength Index of

the shares for 28 days must be worth at least 45 for

not give a sale order if the stock has remained in the

portfolio at least 14 days. The maximum loss allowed

to give an immediate sale order is 4%.

In Table 1 are the results obtained in each one

of the three periods and they are compared with the

revaluation of IBEX 35 in that time. Also is the vari-

ance of the daily revaluation throughout each one of

the periods. We can found that the system achieves

a lower variance than produced by the IBEX 35 and

therefore offers less risk. This is because the intelli-

gent system for tactical asset allocation controls the

behavior of the shares, selling for example those that

have lost over 4%.

To evaluate the importance of the results obtained

with this system, we are going to compare them with

the results of a report elaborated by INVERCO (Span-

ish Association of Investment and Pension Funds).

Table 2 shows the ranking (R) by annual equiva-

lent return (APR) in periods of 1, 3 and 5 years of

each one of the best Spanish equity funds (Foncaixa

Bolsa Espa˜na 150, BBVA Bolsa Ibex Quant, Bank-

inter Bolsa Espa˜na 2, CC Borsa 11, Venture Bol.

TRADINNOVA-FUZ: FUZZY PORTFOLIO INVESTMENT - Dynamic Stock Portfolio Decision-making Assistance

Model based on a Fuzzy Inference System

Table 1: Result of the simulation vs. IBEX35 revaluation.

System Period Result Variance

Simulation 2009 42.94% 1.65

IBEX35 2009 26.22% 2.45

Simulation 2007-2009 5.22% 1.42

IBEX35 2007-2009 -16.92% 3.34

Simulation 2005-2009 104.23% 1.12

IBEX35 2005-2009 30.85% 2.23

Espa˜nola), until 31 December 2009.

Table 2: Ranking of funds from Spanish equity investment

(INVERCO, 2009).

2009 2007-2009 2005-2009

Equity funds APR R APR R APR R

Foncaixa 51.9 1 −8.9 79 − −

BBVA 48.7 2 −13.0 86 − −

Bankinter 34.5 32 4.4 1 11.7 1

CC 19.1 88 2.4 2 4.1 72

Venture 34.9 24 0.0 6 10.6 2

Simulation 42.9 5 1.7 3 15.4 1

In this report elaborated by INVERCO we can see

that the most proﬁtable fund in 2009 was the Fon-

caixa Bolsa Espa

na 150, with a 51.9% of revaluation,

although this fund was ranked in the position 79 by

the return of -8.9% APR that obtained in the 3 pre-

vious years. Our system obtains in 2009 a yield of

42.9%, so that if we could participate in this ranking

we would be included in the ﬁfth position by yield to

one year.

To three years view the stock market crisis con-

tinues nevertheless passing bill, since almost all the

funds register red numbers, except the ﬁrst funds, like

Bankinter Bolsa Espa

na 2, that with a 4.4% APR

would remain ﬁrst inside this ranking of the better

investment funds in Spain for 3 years. Our system

achieves a revaluation of 1.7% APR in this period,

therefore we would remain third in the ranking for

proﬁtability for 3 years.

With a horizon of ﬁve years, the situation is dif-

ferent: some funds, as the mentioned Bankinter Bolsa

Espa

na 2 (11.7% APR) or Venture Bol. Espa

nola

(10.6% APR) obtain notable performances, although

our system surpasses all of these funds with a proﬁt

value of 15.4% APR.

5 CONCLUSIONS

This article has proposed a hybrid intelligent system

that solves quite successful investment in shares form-

ing a portfolio. This system has two main parts: the

ﬁrst is responsible for buying and selling shares, man-

aging a portfolio and monitoring the purchased shares

and the second part is responsible for selecting which

are the best shares to incorporate them into the port-

folio.

The part entrusted to realize the tactical asset al-

location, corresponds to a decision system based on

rules and the part entrusted to select shares has been

based on a fuzzy inference system.

In the obtained results the revaluation of the ref-

erence index is surpassed (IBEX35) in all the periods

and even we can place the hybrid intelligent system

in the ﬁrst positions of the ranking by proﬁt value if

it is compared with commercial investment funds that

invest in Spanish equities.

ACKNOWLEDGEMENTS

Supported by the project TIN2008-06872-C04-03 of

the MICINN of Spain and European Fund for Re-

gional Development.

REFERENCES

Amenc, N. and Sourd, V. L. (2003). Portfolio Theory and

Performance Analysis. Wiley Finance.

Atsalakis, G. and Valavanis, K. (2009). Forecasting stock

market short-term trends using a neuro-fuzzy based

methodology. Expert Systems with Applications,

36(7):10696–10707.

BME (2009). Bolsas y Mercados Espa˜noles. Normalidad de

las series ﬁnancieras. http://www.bolsasymercados.es.

Cheung, W. and Kaymak, U. (2007). A fuzzy logic based

trading system. In Proc. on the 3rd European Sympo-

sium on Nature-inspired Smart Information Systems.

Dourra, H. and Siy, P. (2002). Investment using techni-

cal analysis and fuzzy logic. Fuzzy Sets and Systems,

127(2):221–240.

INVERCO (2009). Asociaci´on de Instituciones de Inversi´on

Colectiva y Fondos de Pensiones. Ranking Fondos

Inversi´on a 31-12-2009. http://www.inverco.es.

Kosko, B. (1992). Neural network and Fuzzy systems. A

dynamical systems approach to machine intelligence.

Prentice Hall Press.

Malkiel, B. (1973). A Random Walk Down Wall Street. W.

W. Norton & Company.

Murphy, J. (1999). Technical Analysis of the Financial Mar-

kets: A Comprehensive Guide to Trading Methods and

Applications. Prentice Hall Press.

Sun, H. and Liu, L. (2002). A linear output structure

for fuzzy logic controllers. Fuzzy Sets and Systems,

131(2):265–270.

ICFC 2010 - International Conference on Fuzzy Computation