
CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM
FOR THE SINGLE MACHINE SCHEDULING PROBLEM
WITH SEQUENCE-DEPENDENT SETUP TIMES
Aymen Sioud, Marc Gravel and Caroline Gagn
´
e
D
´
epartement d’Informatique et Math
´
ematique, Universit
´
e du Qu
´
ebec
´
a Chicoutimi
555 Boulevard Universit
´
e, Chicoutimi, Canada
Keywords:
Hybrid crossover, Constrained based scheduling, Total tardiness, Single machine.
Abstract:
This paper presents a hybrid approach based on the integration between Genetic Algorithm (GA) and Con-
straint Based Scheduling (CBS) approaches for solving a scheduling problem. The main contributions are the
integration of the CBS approach in the reproduction and the intensification processes of a GA autonomously.
The proposed methodology is applied to a single machine scheduling problem with sequence-dependent setup
times for the objective of minimizing the total tardiness. A sensitivity analysis of the hybrid methodology
is carried out to compare the performance of the GA and the integrated GA-CBS approaches on different
benchmarks from the literature.
1 INTRODUCTION
Several researches on scheduling problems have been
done under the assumption that setup times are inde-
pendent of job sequence. However, in certain con-
texts, such as the pharmaceutical industry, metallur-
gical production, electronics and automotive manu-
facturing, there are frequently setup times on equip-
ment between two different activities. Production of
good schedules often relies on management of these
setup times (Allahverdi et al., 2008). This present
paper considers the single machine scheduling prob-
lem with sequence dependent setup times with the ob-
jective to minimize total tardiness of the jobs (SMS-
DST). This problem, noted as 1|s
i j
|ΣT
j
in accordance
with the notation of Graham, Lawler, Linstra and Ri-
nooy Kan (1979) , is an NP-hard problem (Du and
Leung, 1990).
The 1|s
i j
|ΣT
j
may be defined as a set of n jobs
available for processing at time zero on a continu-
ously available machine. Each job j has a processing
time p
j
, a due date d
j
, and a setup time s
i j
which is
incurred when job j immediately follows job i. It is
assumed that all the processing times, due dates and
setup times are non-negative integers. A sequence of
the jobs S = [q
0
, q
1
,..., q
n−1
, q
n
] is considered where
q
j
is the subscript of the j
th
job in the sequence. The
due date and the processing time of the j
th
job in se-
quence are denoted as d
q
j
and p
q
j
, respectively. Thus,
the completion time of the j
th
job in sequence will be
expressed as C
q
j
=
∑
j
k=1
(s
q
k−1
q
k
+ p
q
k
) while the tar-
diness of the j
th
job in sequence will be expressed as
T
q
j
= max(0, C
q
j
−d
q
j
). The objective of the schedul-
ing problem studied is to minimize the total tardiness
of all the jobs which will be expressed as
∑
n
j=1
T
q
j
.
In this paper, we present a hybrid approach based
on Genetic Algorithm (GA) and Constraint Based
Scheduling (CBS) to solve this problem. The CBS
approach has become a widely used form for model-
ing and solving scheduling problems using the con-
straint programming approach. The hybridization of
the CBS approach with the GA is done at two levels.
Indeed, the CBS is used in the reproduction and inten-
sification processes of GA separately and this repre-
sents the paper’s main contributions. In fact, the CBS
approach is integrated in a crossover operator and in
the intensification search space process using addi-
tional constraints for both of them. Computational
testing is performed on a set of test problems avail-
able from literature. We report on our experimental
results and conclude with some remarks and future
research directions. As a constraint programming en-
vironment, we use the ILOG IBM CP environment
using ILOG Solver and ILOG Scheduler via the C++
APIs (ILOG, 2003b; ILOG, 2003a). The use of this
kind of platforms has been encouraged by the steady
137
Sioud A., Gravel M. and Gagné C..
CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING PROBLEM WITH SEQUENCE-
DEPENDENT SETUP TIMES.
DOI: 10.5220/0003060601370145
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 137-145
ISBN: 978-989-8425-31-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

improvement of general purpose solvers over the past
decade. Such solvers have become significantly more
effective and robust (Yunes et al., 2010). Also, the
C++ APIs allow users to develop their own strategies
for a particular problem. Moreover, this interface en-
ables a better interaction with other applications than
the OPL interface (ILOG, 2003b).
2 LITERATURE REVIEW
Considering the objective of minimizing the
makespan in the basic single machine problem
without setup times, any permutation of jobs gives
the same makespan. Nevertheless, the addition of
the sequence dependent setup times considerably
complicates the problem (Allahverdi et al., 2008).
This problem with the objective of minimizing the
makespan is equivalent to the Travelling Salesman
Problem (TSP), which is NP-hard. In addition, this
problem is even more difficult when total tardiness
is the performance measure and there has been
relatively little research reported on it. Furthermore,
in presence of sequence dependent setup times, most
of the research has focused on either minimizing the
sum of setup times or minimizing the sum of job
completion times (Allahverdi et al., 2008).
Different approaches have been proposed by a
number of researchers to solve the problem. Rubin
and Ragatz (1995) proposed a Branch and Bound ap-
proach, which quickly showed its limitations. It could
solve to the optimality only small instances of bench-
mark files of 15, 25, 35 and 45 jobs proposed by these
authors. Bigras, Gamache and Savard (2008) solved
to the optimum all instances proposed by Rubin and
Ragatz (1995) using a Branch and Bound approach
with linear programming relaxation bounds. They
also demonstrated and used the problem’s similarity
with the time-dependent traveling salesman problem.
Such Branch and Bound approach solved some of
these instances by more than 7 days. Because this
problem is NP-hard, many researchers used a wide
variety of metaheuristics to solve this problem such
as genetic algorithm (Franca et al., 2001; Sioud et al.,
2009), memetic algorithm (Armentano and Mazzini,
2000; Franca et al., 2001; Rubin and Ragatz, 1995),
simulated annealing (Tan and Narasimhan, 1997),
GRASP (Gupta and Smith, 2006), ant colonies op-
timization (Gagn
´
e et al., 2002; Liao and Juan, 2007)
and Tabu/VNS (Gagn
´
e et al., 2005). Heuristics such
as Random Start Pairwise Interchange (RSPI) (Rubin
and Ragatz, 1995) and Apparent Tardiness Cost with
Setups (ATCS) (Lee et al., 1997) have also been pro-
posed for solving this problem. For their part, Spina,
Galantucci and Dassisti (2003) introduce a hybrid ap-
proach using constraint programming and genetic al-
gorithm sequentially. In this latter case, the authors
have considered a real world problem with a maxi-
mum of ten jobs.
3 THE HYBRID GENETIC
ALGORITHM
In their respective works, Rubin and Ragatz (1995)
and Sioud, Gravel and Gagn
´
e (2009) have shown the
importance of relative and absolute order positions for
the 1|s
i j
|ΣT
j
problem. Thereby, all the used crossover
operators into the genetic algorithms from literature
maintain the absolute position, or the relative posi-
tion or both. Indeed, Rubin and Ragatz (1995) used
a specific operator which alters the conservation of
the absolute and the relative order by generating ran-
dom sub-sequences of jobs separately for each off-
spring. Armentano and Mazzini (2000) modified the
ERX crossover while Franca, Mendes and Moscato
(2001) developed a genetic and a memetic algorithms
using the OX crossover. Sioud et al. (2009) proposed
RMPX, a new crossover operator which takes greater
account of the relative and absolute position job and
gives better results than other crossovers.
To reach good results, the presented hybrid ge-
netic algorithm must ensure the preservation of both
the relative and the absolute order positions while
maintaining diversification during its evolving. In this
context, the genetic algorithm and the two hybridiza-
tion approaches will take this into consideration.
3.1 Genetic Algorithm
Genetic algorithms are methods based upon bio-
logical mechanisms such as the genetic inheritance
laws of Mendel and the natural selection concept of
Charles Darwin, where the best adapted species sur-
vive. The basic concepts of GA have been described
by the investigation carried out by Holland (1992)
who explained how to add intelligence into a program
computing with the crossover exchange of genetic
material and transfer as a source of genetic diversity.
In a GA, a population of individuals or chromosomes
incurs a sequence of transformations by means of ge-
netic operators to form a new population. Two main
operators are used for this purpose : crossover and
mutation. Crossover creates new individuals by com-
bining parts of two individuals and mutation creates
new individuals by a small change in a single individ-
ual.
Based on the GA proposed by Sioud et al. (2009),
ICEC 2010 - International Conference on Evolutionary Computation
138

we redefine a simple genetic algorithm. A solution
is coded as a permutation of the considered jobs. The
population size is set to n to fit with the considered in-
stance size. The initial population is randomly gener-
ated for 60% and also for 20% using a pseudo-random
heuristic which favors setup times and promotes a rel-
ative order for the jobs. The last 20% is generated
using a pseudo-random heuristic which depends on
due dates and promotes an absolute order for the jobs.
A binary tournament selects the chromosomes for the
crossover. The proposed GA uses the OX crossover
(Michalewicz, 1996) to generate 30% of offspring and
the RMPX crossover (Sioud et al., 2009) to generate
the rest of the children population. Both of the OX
and RMPX crossover maintain both of the relative and
the absolute order positions, but the RMPX crossover
seems to give better results. The RMPX crossover can
be described in the following steps : (i) two parents
P1 and P2 are considered and two distinct crossover
points C1 and C2 are selected randomly, as shown in
Figure 1; (ii) an insertion point p
i
is then randomly
chosen in the offspring E as p
i
= random (n – ( C2 –
C1)); (iii) the part [C1, C2] of P1, shaded in Figure 1,
is inserted in the offspring E from p
i
. The insertion is
to be done from the position 2 showing in Figure 1;
and (iv) the rest of the offspring E is completed from
P2 in order of appearance since its first position.
3 7658241P1
P2
C2
C1
8 2461375
7 6135824E
p
i
Figure 1: Illustration of RMPX.
The crossover probability pc is set to 0.8, i.e.
therefore n*0.8 offspring are generated at each gener-
ation in which a mutation is applied with a probability
pm equal to 0.3. The mutation consists of exchanging
the position of two distinct jobs which are randomly
chosen. The replacement is elitist and the duplicates
individuals in the population were replaced by chro-
mosomes which are generated by one of the pseudo-
random heuristics used in the initialization phase. The
stop criterion is set to 3000 generations.
3.2 Constraint based Scheduling
Constraint solving methods such as domain reduc-
tion and constraint propagation have proved to be
well suited for a wide range of industrial applications
(Fromherz, 1999). These methods are increasingly
combined with classical solving techniques from op-
erations research, such as linear, integer, and mixed
integer programming (Talbi, 2002), to yield power-
ful tools for constraint-based scheduling by adopting
them. The most significant advantage of using such
CBS is to separate the model from the algorithms
which solve the scheduling problem. This makes it
possible to change the model without changing the
algorithm used and vice versa.
In the recent years, the CBS has become a widely
used form for modeling and solving scheduling prob-
lems using the constraint programming approach
(Baptiste et al., 2001; Allahverdi et al., 2008). A
scheduling problem is the process of allocating tasks
to resources over time with the goal of optimizing
one or more objectives (Pinedo, 2002). A scheduling
problem can be efficiently encoded like a constraint
satisfaction problem (CSP).
The activities, the resources and the constraints,
which can be temporal or resource related, are the
basis for modeling a scheduling problem in a CBS
problem. Based on representations and techniques
of constraint programming, various types of variables
and constraints have been developed specifically for
scheduling problems. Indeed, the domain variables
may include intervals domains where each value rep-
resents an interval (processing or early start time for
example) and variable resources for many classes of
resources. Similarly, various research techniques and
constraints propagation have been adapted for this
kind of problem.
In Constraint Based Scheduling, the single ma-
chine problem with setup dependent times can be effi-
ciently encoded in terms of variables and constraints
in the following way. Let M be the single resource.
We associate an activity A
j
for each job j. For each
activity A
j
four variables are introduced, start(A
j
),
end(A
j
), proc(A
j
) and dep(A
j
). They represent the
start time, the end time, the processing time and the
departure time of the activity A
j
, respectively. The
departure time represents the needed setup time of an
activity when the latter starts the schedule.
A setup time s
i j
is introduced and it is incurred
when job j immediately follows job i. In our case,
the setup times are activity related and not resource-
related. For this purpose, we assign a type to each ac-
tivity and a lattice to the unary machine. Then, when
we calculate the objective function, it is possible to
CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING
PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES
139

Figure 2: C++ API model for the 1|s
i j
|ΣT
j
problem.
associate the transition times between two distinct
types of activities. The tardiness criterion is repre-
sented by an additional variable Tard. Its value is de-
termined by Tard =
∑
n
A
j
=1
max(end(A
j
) − d
A
j
, 0).
Figure 2 presents the pseudo-code for the 1|s
i j
|ΣT
j
problem modeling with the C++ API of ILOG Sched-
uler 6.0. The main procedure ModelSMSDST calls
the two procedures CreateMachine and CreateJob.
CreateMachine procedure (lines 3 to 6) uses the class
IloUnaryResource. This allows handling unary re-
sources, that is to say, a resource whose capacity is
equal to one. This resource cannot therefore handle
more than one job at a time. The use of the setup times
in CBS and also with ILOG Scheduler 6.0 (ILOG,
2003a) indicates that they are resource-related and not
activity-related such as is the case in our problem. It
is possible to overcome this problem by associating a
type for each activity and creating setup times asso-
ciated with these types. For this purpose, we use the
class IloTransitionParam which is managing and set-
ting setup times. The setup matrix is then associated
to this class which will be related to the unary ma-
chine (line 5). Thus, when we calculate the objective
function, it is possible to associate the setup times be-
tween two distinct types of activities. To model the
total tardiness, we must first define a variable Tard
(line 16). Then we define an array C containing the
completion times C
i
of the different activities times A
i
during the research phase (line 15). When we create
the activities in the model, we add a constraint that
combines the activities A
i
to the corresponding times
C
i
(line 19). After that, we add a constraint which
combines the variable Tard with the sum of the C
i
in
the table C (line 21). Finally, we add a constraint that
minimizes the variable Tard (line 22). Thus, we ob-
tain the objective function which will be added to the
model.
ILOG Solver (2003) provides several predefined
search algorithms named as goals and activity se-
lectors. We used the IloSetTimesForward algorithm
with the IloSelFirstActMinEndMin activity selector.
The IloSetTimesForward algorithm schedules activi-
ties on a single machine forward initializing the start
time of the unscheduled activities. The activity se-
lector defines the heuristic scheduling variables rep-
resenting start times, which chooses the next activ-
ity to schedule. The IloSelFirstActMinEndMin tries
first the activity with the smallest start time and in
case of equality the activity with the smallest end
time. For his part, ILOG Scheduler (2003) provides
four strategies to explore the search tree : the default
Depth-First Search (DFS), the Slice-Based Search
(SBS) (Beck and Perron, 2000), Interleaved Depth-
First Search (IDFS) (Meseguer, 1997) and the Depth-
Bounded Discrepancy Search (DDS) (Walsh, 1997)
which is used in this work.
ICEC 2010 - International Conference on Evolutionary Computation
140

3.3 Hybrid Approach
The hybridization of an exact method such as the
CBS and a metaheuristic such as the GA can be car-
ried out in several ways. Talbi (2002) presents a
taxonomy dealing with the hybrid metaheuristics in
general. Puchinger and Raidl (2005) and Jourdan,
Basseur and Talbi (2009) present a taxonomy for the
exact methods and metaheuristics hybridizing. In
this paper we present two different approaches of hy-
bridization. The first approach is to integrate the CBS
in the GA reproduction phase and more precisely in
a crossover operator, while the second approach is to
use CBS as an intensification process in the GA.
When we handle a basic single machine model,
there is no precedence constraint between activities
as is the case in a flow-shop or job-shop where adding
constraints improves the CBS approach. The main
idea of integrating the CBS in a crossover is to provide
to this latter precedence constraints between activi-
ties when generating offspring. In this work, we con-
sider only the direct constraints during the crossover.
Therefore, the conceived crossover promotes the rel-
ative order positions such as the PPX crossover (Bier-
wirth et al., 1996). The proposed crossover operator is
designated Precedence Constraint Crossover (PCX)
and can be described in the two following steps : (i)
two parents P1 and P2 are considered and the prece-
dence constraints between activities concurrently in
both parents are kept, as shown in Figure 3; and (ii)
the CBS approach tries to solve the problem while
adding the precedence constraints built in the previous
step and an upper bound consisting of the objective
function value of the best parent. The upper bound is
added to discard faster bad solutions when branching
during the solver process. As a reminder, the ILOG
Solver uses a Branch and Bound approach to solve
a problem (ILOG, 2003b). In the case of Figure 3,
the two precedence constraints (4 before 6) and (7 be-
fore 5) are added to the model and will be propagated.
Thus, these two constraints, preserve the relative po-
sitions of the pairs of activities (4,6) and (7,5). E1, E2
and E3 represent three potential offspring where the
two precedence constraints (4 before 6) and (7 before
5) are preserved. Then, if the two selected parents are
”good” solutions, preserving the relative order could
in turn generate also ”good” solutions. Finally, if no
solution is found by the PCX crossover, the offspring
is generated by one of the pseudo-random heuristics
used in the initialization phase. The PCX crossover
will be done under probability p
PCX
.
Integrating an intensification process in a genetic
algorithm has been applied successfully in several
fields. The incorporation of heuristics and/or other
methods, i.e. an exact method such as the CBS ap-
proach, into a genetic algorithm can be done in the
initialization process to generate well-adapted initial
population and/or in the reproduction process to im-
prove the offspring quality fitness. Following this lat-
ter reasoning, the strategy proposed in this paper is
based on the intensification in specific space search
areas. However, we can find in literature only few pa-
pers dealing with such hybridization (Puchinger and
Raidl, 2005; Talbi, 2009).
4 1285736P1
2 5716483P2
7 3126485E1
7 2381645E2
8 1572364E3
Figure 3: Illustration of PCX.
In the same vein of the PCX conservation prece-
dence constraints, an intensification process is applied
by giving a generated offspring to the CBS approach
and fixing a block of α positions. Thus, the abso-
lute order position will be preserved for these fixed
positions while the relative order position will be pre-
served for the other activities. Indeed, the activities
on the left of the fixed block will be scheduled before
this late block, while the activities on the right will
be scheduled after this block. The fixed block size
should be neither too large nor too small : if its size is
too large, the CBS approach will have no effect and if
its size is too small the CBS approach will consume
more time to find a better solution. Thereby, at each
time this intensification is done, α continuous posi-
tions are fixed with 0.2*n ≺ α ≺ 0.4*n. We use to
this end two different procedures based on the CBS
approach. The first one, noted as IP
TARD
, selects a
generated offspring and tries to solve the problem us-
ing the CBS approach which minimizes the total tar-
diness described above while adding an upper bound
consisting of the objective function value of this off-
spring. So as a result, the CBS approach may return a
better solution when scheduling separately the activi-
ties on the left and the right of the fixed block activi-
ties.
CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING
PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES
141
Using the similarity of the studied problem with
the time-dependent traveling salesman problem (Bi-
gras et al., 2008), the second intensification proce-
dure, noted as IP
T SP
, works like IP
TARD
but in this
case the CBS approach minimizes the makespan. The
makespan optimization aims to minimize the setup
times and then, in some specific configurations, will
give promising solutions under total tardiness opti-
mization otherwise explore a different areas search
space. The makespan criterion is represented by an
additional variable Makespan. Its value is determined
by Makespan =
∑
n
A
j
=1
max(end(A
j
)). The model
minimizing the makespan is similar to that in Fig-
ure 2. Indeed, we just delete the declaration of the
array C at line 15 and define an activity Makespan
with time processing equal to 0 at line 16. Then, a
constraint stating that all jobs must be completed be-
fore the Maskespan start time is added in the for loop.
Finally, lines 19 and 21 are removed and line 22 min-
imizes in this case the Makespan end time.
Thereby, an offspring is selected with a tourna-
ment under probability p
IP
and then, one of the two
intensification procedures IP
TARD
and IP
T SP
is chosen
under probability p
cip
to be applied on this offspring.
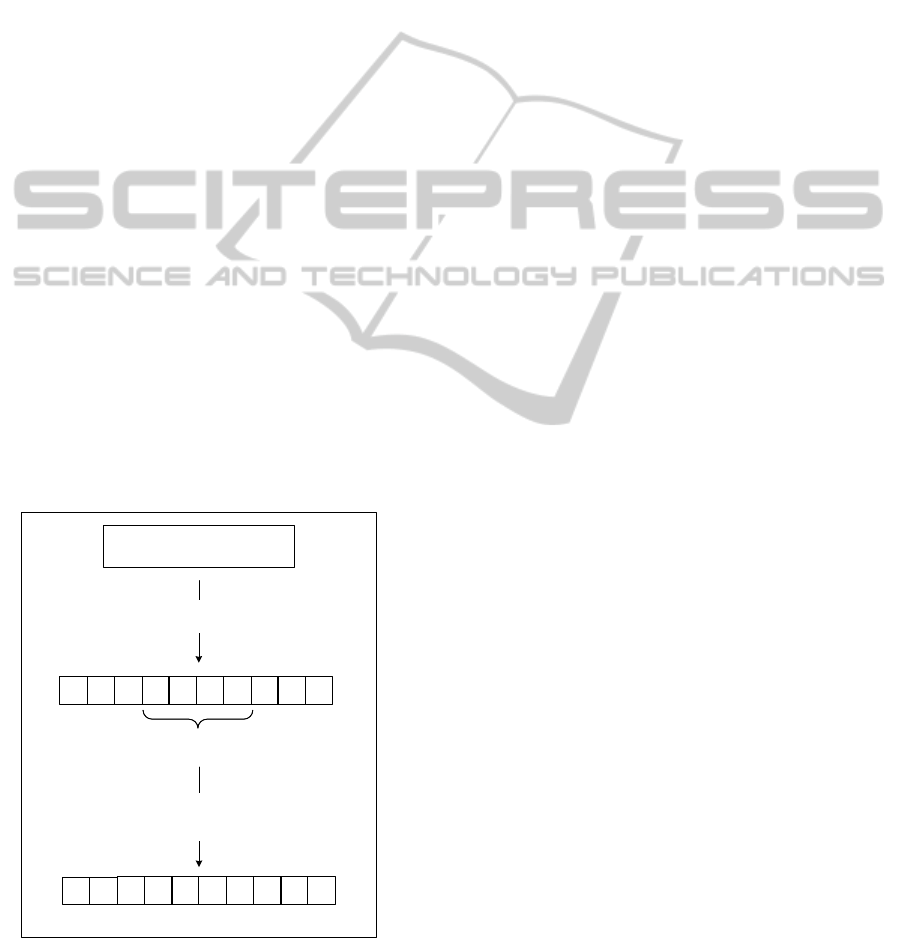
Figure 4 illustrates the intensification process based
on the CBS approach. At each generation, an off-
spring is selected under probability p
IP
with tourna-
ment selection. After fixing α positions and choosing
an intensification procedure, IP
TARD
or IP
T SP
under
probability p
cip
, the solver tries to find a solution. If
no solution is found the offspring is unchanged.
Population (t)
α fixed positions
Tournament selection
under probability p
IP
Final offspring
Choose and apply an intensification
procedure under probability p
cip
Figure 4: The intensification process.
4 COMPUTATIONAL RESULTS
AND DISCUSSION
The benchmark problem set consists of eight in-
stances, each with a number of jobs of 15, 25, 35
and 45 jobs, and it is taken from the work of Ragatz
(1993). These instances are available on the Inter-
net at https://www.msu.edu/˜rubin/files/c&ordata.zip.
The job processing times are normally distributed
with a mean of 100 time units and the setup times
are also uniformly distributed with a mean of 9.5 time
units. Each instance has three factors which have both
high and low levels. These factors are due date range,
processing time variance and tardiness factor. The tar-
diness factor determines the expected proportion of
jobs that will be tardy in a random sequence. All the
experiments were run on an Itanium with a 1.4 GHz
processor and 4 GB RAM. Each instance was exe-
cuted 5 times and the results presented represent the
average deviation with the optimal results of Bigras
et al. (2008) . All the algorithms are coded in C++
language under the ILOG IBM CP constraint environ-
ment using ILOG Solver and Scheduler via the C++
API (ILOG, 2003b; ILOG, 2003a).
Table 1 compares the results of different ap-
proaches. In this table, PRB denotes the instance
names and OPT the optimal solution found by the
B&B of Bigras et al. (2008). These authors have not
given information about the execution time of their
approach. They only said that some instances have
been resolved after more than seven days. The GA
column shows the results average deviation to the op-
timal solution of the genetic algorithm described in
the section 3.1 which gives the best results among all
genetic algorithms in the literature without an inten-
sification process (Sioud et al., 2009). The GA av-
erage CPU time is equal to 13.4 seconds for the 32
instances. The GA generally obtained fairly good re-
sults only for the instances 601, 605, 701 and 705.
These instances are low due date range and large tar-
diness factor. Thus, for this kind of instances, ”good”
solutions may not generate ”good” offspring. Further-
more, considering that the tardy jobs are scheduled at
the end of the sequence, it may be sufficient to sched-
ule the other jobs by minimizing the setup times. It is
the aim of introducing the IP
T SP
intensification pro-
cedures.
The CBS column shows the deviations of the CBS
approach minimizing the total tardiness defined in
Section 3.2. For this approach, the execution time
is limited to 60 minutes. It can be noticed that the
CBS approach results deteriorate with increasing the
instances size and especially for the **4, **5 and **8
instances. The GA
PCX
column shows the average de-
ICEC 2010 - International Conference on Evolutionary Computation
142

Table 1: Comparison of different algorithms.
PRB OPT GA CBS GA
PCX
GA
IP
GA
HY B
401 90 0.0 0.0 0.0 0.0 0.0
402 0 0.0 0.0 0.0 0.0 0.0
403 3418 0.5 0.0 0.0 0.4 0.0
404 1067 0.0 0.0 0.0 0.0 0.0
405 0 0.0 0.0 0.0 0.0 0.0
406 0 0.0 0.0 0.0 0.0 0.0
407 1861 0.0 0.0 0.0 0.0 0.0
408 5660 0.2 0.9 0.0 0.1 0.0
501 261 0.5 0.4 0.0 0.5 0.0
502 0 0.0 0.0 0.0 0.0 0.0
503 3497 0.2 2.5 0.0 0.3 0.0
504 0 0.0 0.0 0.0 0.0 0.0
505 0 0.0 0.0 0.0 0.0 0.0
506 0 0.0 0.0 0.0 0.0 0.0
507 7225 0.7 1.8 0.0 0.7 0.0
508 1915 0.0 35.8 0.0 1.8 0.0
601 12 169.4 41.7 6.7 7.5 3.3
602 0 0.0 0.0 0.0 0.0 0.0
603 17587 1.8 6.5 0.8 1.1 0.2
604 19092 1.8 21.1 1.1 1.3 0.6
605 228 13.0 122.4 2.6 3.5 0.4
606 0 0.0 0.0 0.0 0.0 0.0
607 12969 1.6 17.7 0.7 1.9 0.2
608 4732 1.7 156.6 0.7 1.2 0.0
701 97 30.7 20.6 6.8 8.3 2.1
702 0 0.0 0.0 0.0 0.0 0.0
703 26506 1.9 2.8 1.2 1.8 0.9
704 15206 3.4 94.8 1.6 2.1 0.5
705 200 33.7 72.5 6.1 6.5 2.2
706 0 0.0 0.0 0.0 0.0 0.0
707 23789 2.2 20.4 1.0 1.9 0.3
708 22807 2.8 50.0 1.5 2.1 1.2
viation of the genetic algorithm in which the crossover
operator PCX is integrated. The probability p
PCX
is
equal to 0.2 and the CBS approach execution time is
limited to 15 seconds. The GA
PCX
average time ex-
ecution is equal to 15.2 minutes for the 32 instances.
The first observation is that the GA
PCX
algorithm is
always optimal for 15 and 25 jobs instances. It should
be noted that the integration of the PCX crossover im-
proves all of the GA results and especially for the
instances **1 and **5 where the deviation became
less than 7%. For example, the deviation was re-
duced from 169.4% to 6.7% for the 601 instance. Us-
ing the direct precedence constraints allows the PCX
crossover to enhance both the GA exploration and the
CBS search; and consequently reaching better sched-
ules.
The GA
IP
column shows the average deviation of
the genetic algorithm in which we include the IP
Tard
and IP
T SP
intensification procedures under probabil-
ity p
IP
equal to 0.1. The CBS approach execution
time is limited to 20 seconds for the IP
Tard
and IP
T SP
.
The GA
IP
average time execution is equal to 16.5
minutes for the 32 instances. The GA
IP
improves
most GA results and specially the **1 and **5 in-
stances but gives worse results than the GA
PCX
and
this was expected because in 50% of the cases the in-
tensification procedure minimizes the makespan and
not the total tardiness.
The GA
HY B
column shows the average deviation
of the GA
PCX
algorithm where we include the IP
Tard
and IP
T SP
intensification procedures. The probabil-
ities p
IP
and p
cip
are equal to 0.1 and 0.5 respec-
tively like the GA
IP
. The CBS approach execution
time is also limited to 20 seconds for the IP
Tard
and
IP
T SP
in the GA
HY B
. The GA
HY B
average time exe-
cution is equal to 24.5 minutes for the 32 instances.
This hybrid algorithm improves all the results found
by the GA
PCX
. These improvements are more pro-
CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING
PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES
143

nounced with the integration of local search proce-
dures. The introduction of the two intensification pro-
cedures improves essentially the **1 and the **5 in-
stances. Also, the optimal schedule is always reached
by GA
HY B
for the 608 instance. The GA
HY B
found
the optimal solution for all the instances at least one
time and this was not the case either for GA
PCX
or
GA
IP
.
The convergence of both GA and the GA
PCX
al-
gorithms are similar. Indeed, the average conver-
gence generation is equal to 1837 and 1845 genera-
tions for GA and GA
PCX
, respectively. Concerning
the GA
IP
algorithm, the average convergence gener-
ation is equal to 1325 generations. So, we can con-
clude that the two intensification procedures based
on the CBS approach are permitting a faster genetic
algorithm convergence than the PCX crossover but
achieving worse results. The GA
HY B
average conver-
gence generation is equal to 825 and compared to the
GA
PCX
, the introduction of the intensification proce-
dures speeds up the convergence of the solution with
reaching better results.
Exact methods are well known to be time ex-
pensive. The same applies to their hybridization of
them with metaheuristics. Indeed, times execution in-
creases significantly with such hybridization policies
due to some technicality during the exchange of infor-
mation between the two methods (Talbi, 2009; Talbi,
2002; Puchinger and Raidl, 2005; Jourdan et al.,
2009) and this is what has been observed here. How-
ever, in this paper, the solution quality is our main
concern. So, we concentrated our efforts on it.
5 CONCLUSIONS
In this paper, we describe the hybridization into a
Genetic Algorithm of both a crossover operator and
intensification process based on Constraint Based
Scheduling. The PCX crossover operator uses the
direct precedence constraints to improve the CBS
search and consequently the schedules quality. The
precedence constraints are built from the selected par-
ents information in the reproduction process.
The intensification procedures are based on two
different CBS approaches after fixing a jobs block :
the first minimizes the total tardiness which represents
the considered problem objective function while the
second minimizes the makespan which also enhances
the exploration process and is well adapted to some
instances. These three policies hybridization repre-
sent the main contribution of this paper.
Compared to a simple GA, the use of the PCX
crossover improves all the results but for some in-
stances the difference is still noticeable. The hybrid
algorithm which uses the PCX crossover and the in-
tensification process improves the results and speeds
up the convergence of the solution. These results sug-
gest that the latter model seems to outperform the sin-
gle GA, the genetic algorithm with the hybrid PCX
crossover and the genetic algorithm with the intensi-
fication process.
A possible area of research in the future would
be to improve the precedence constraints quality. In-
deed, it is possible to consider constraints related to
a jobs set or to intervals time and indirect constraint.
Another possible area for further research would be
to employ a chromosome representation based on the
start times of activities. Hence, it will be possible to
get more accurate combination of start times.
REFERENCES
Allahverdi, A., Ng, C., Cheng, T., and Kovalyov, M. Y.
(2008). A survey of scheduling problems with setup
times or costs. European Journal of Operational Re-
search, 187(3):985 – 1032.
Armentano, V. and Mazzini, R. (2000). A genetic algo-
rithm for scheduling on a single machine with setup
times and due dates. Production Planning and Con-
troly, 11(7):713 – 720.
Baptiste, P., LePape, C., and Nuijten, W. (2001).
Constraint-Based Scheduling : Applying Constraint
Programming to Scheduling Problems. Kluwer Aca-
demic Publishers.
Beck, J. C. and Perron, L. (2000). Discrepancy bounded
depth first search. In CP-AI-OR’2000: Fourth Inter-
national Workshop on Integration of AI and OR Tech-
niques in Constraint Programming for Combinatorial
Optimization Problems, pages 7–17.
Bierwirth, C., Mattfeld, D. C., and Kopfer, H. (1996). On
permutation representations for scheduling problems.
In PPSN IV: Proceedings of the 4th International
Conference on Parallel Problem Solving from Nature,
pages 310–318, London, UK. Springer-Verlag.
Bigras, L., Gamache, M., and Savard, G. (2008). The time-
dependent traveling salesman problem and single ma-
chine scheduling problems with sequence dependent
setup times. Discrete Optimization, 5(4):663–762.
Du, J. and Leung, J. Y. T. (1990). Minimizing total tar-
diness on one machine is np-hard. Mathematics and
Operations Researchs, 15:438–495.
Franca, P. M., Mendes, A., and Moscato, P. (2001). A
memetic algorithm for the total tardiness single ma-
chine scheduling problem. European Journal of Op-
erational Research, 132:224–242.
Fromherz, M. P. (1999). Model-based configuration of ma-
chine control software. Technical report, In Configu-
ration Papers from the AAAI Workshop.
ICEC 2010 - International Conference on Evolutionary Computation
144

Gagn
´
e, C., Gravel, M., and Price, W. L. (2005). Using meta-
heuristic compromise programming for the solution of
multiple objective scheduling problems. The Journal
of the Operational Research Society, 56:687–698.
Gagn
´
e, C., Price, W., and Gravel, M. (2002). Comparing an
aco algorithm with other heuristics for the single ma-
chine scheduling problem with sequence-dependent
setup times. Journal of the Operational Research So-
ciety, 53:895–906.
Graham, R. L., Lawler, E. L., Lenstra, J. K., and Kan, A. G.
H. R. (1979). Optimization and approximation in de-
terministic sequencing and scheduling: a survey. An-
nals of Discrete Mathematics, 5:287–326.
Gupta, S. R. and Smith, J. S. (2006). Algorithms for sin-
gle machine total tardiness scheduling with sequence
dependent setups. European Journal of Operational
Research, 175(2):722–739.
Holland, J. H. (1992). Adaptation in natural and artificial
systems. MIT Press, Cambridge, MA, USA.
ILOG (2003a). ILOG Scheduler 6.0. User Manual. ILOG.
ILOG (2003b). ILOG Solver 6.0. User Manual. ILOG.
Jourdan, L., Basseur, M., and Talbi, E.-G. (2009). Hy-
bridizing exact methods and metaheuristics: A tax-
onomy. European Journal of Operational Research,
199(3):620–629.
Lee, Y., Bhaskaram, K., and Pinedo, M. (1997). A
heuristic to minimize the total weighted tardiness with
sequence-dependent setups. IIE Transactions, 29:45–
52.
Liao, C. and Juan, H. (2007). An ant colony opti-
mization for single-machine tardiness scheduling with
sequence-dependent setups. Computers and Opera-
tions Research, 34:1899–1909.
Meseguer, P. (1997). Interleaved depth-first search. In
IJCAI’97: Proceedings of the Fifteenth international
joint conference on Artifical intelligence, pages 1382–
1387, San Francisco, CA, USA. Morgan Kaufmann
Publishers Inc.
Michalewicz, Z. (1996). Genetic algorithms + data struc-
tures = evolution programs (3rd ed.). Springer-Verlag,
London, UK.
Pinedo, M. (2002). Scheduling Theory, Algorithm and Sys-
tems. Prentice-Hall.
Puchinger, J. and Raidl, G. R. (2005). Combining meta-
heuristics and exact algorithms in combinatorial opti-
mization: A survey and classification. In Proceedings
of the First International Work-Conference on the In-
terplay Between Natural and Artificial Computation,
Las Palmas, Spain, LNCS.
Ragatz, G. L. (1993). A branch-and-bound method for
minimumtardiness sequencing on a single processor
with sequence dependent setup times. In Proceedings
twenty-fourth annual meeting of the Decision Sciences
Institute, pages 1375–1377.
Rubin, P. and Ragatz, G. (1995). Scheduling in a sequence-
dependent setup environment with genetic search.
Computers and Operations Research, 22:85–99.
Sioud, A., Gravel, M., and Gagn
´
e, C. (2009). New
crossover operator for the single machine schedul-
ing problem with sequence-dependent setup times. In
GEM’09: The 2009 International Conference on Ge-
netic and Evolutionary Methods.
Spina, R., Galantucci, L., and Dassisti, M. (2003). A hy-
brid approach to the single line scheduling problem
with multiple products and sequence-dependent time.
Computers and Industrial Engineering, 45(4):573 –
583.
Talbi, E. (2002). A taxonomy of hybrid metaheuristics.
Journal of Heuristics, 8:541–564.
Talbi, E.-G. (2009). Metaheuristics : from design to imple-
mentation. John Wiley & Sons.
Tan, K. and Narasimhan, R. (1997). Minimizing tardi-
ness on a single processor with setup-dependent setup
times: a simulated annealing approach. Omega,
25:619 – 634.
Walsh, T. (1997). Depth-bounded discrepancy search. In
IJCAI’97: Proceedings of the Fifteenth international
joint conference on Artifical intelligence, pages 1388–
1393, San Francisco, CA, USA. Morgan Kaufmann
Publishers Inc.
Yunes, T., Aron, I. D., and Hooker, J. N. (2010). An Inte-
grated Solver for Optimization Problems. Operations
Resaearch, 58(2):342–356.
CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING
PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES
145
