
IMPLICIT SEQUENCE LEARNING
A Case Study with a 4–2–4 Encoder Simple Recurrent Network
Stefan Gl¨uge, Ronald B¨ock and Andreas Wendemuth
Faculty of Electrical Engineering and Information Technology - Cognitive Systems
Otto von Guericke University Magdeburg, Universit¨atsplatz 2, 39106 Magdeburg, Germany
Keywords:
Implicit sequence learning, Temporal order in associative learning, Elman network, Simple recurrent network.
Abstract:
Without any doubt the temporal order inherent in a task is an important issue during human learning. Re-
current neural networks are known to be a useful tool to model implicit sequence learning. In terms of the
psychology of learning, recurrent networks might be suitable to build a model to reproduce the data obtained
from experiments with human subjects. Such model should not just reproduce the data but also explain it and
further make verifiable predictions. Therefore, one basic requirement is an understanding of the processes in
the network during learning. In this paper, we investigate how (implicitly learned) temporal information is
stored/represented in a simple recurrent network. To be able to study detailed effects we use a small network
and a standard encoding task for this study.
1 INTRODUCTION
Temporal order plays an important role in human
learning, e.g. humans tend to use the serial order in
free recall (Mandler and Dean, 1969). Even if the
temporal component is learned implicitly it helps us
to solve the task. Arthur Reber investigated the phe-
nomenon of implicit learning using finite state gram-
mars. In sequential reaction time tasks he could show
that test persons learn the rules of an underlying gram-
mar implicitly (Reber, 1989).
Axel Cleeremans provides a formal model for im-
plicit sequence learning based on connectionist the-
ory. The model applies a simple recurrent network
(SRN), also known as Elman network, and fits the
network’s behaviour to the experimental data of Re-
ber (Cleeremans, 1993).
A SRN is very similar to a common multilayer
feedforward network. It involves additional recurrent
links to provide the network with a dynamic memory.
Therefore it is able to recognise the temporal proper-
ties of a sequential input (Elman, 1990).
The prediction capabilities of the SRN were eval-
uated by Lalit Gupta and Mark McAvoy (Gupta and
McAvoy, 2000). They focus on the prediction of non–
orthogonal vector components of real temporal se-
quences. This leads to a number of applications in
the field of signal classification (
¨
Ubeyli and
¨
Ubeyli,
2008). Another area for the application of SRNs is
autonomous robot control (Sluˇsn´y et al., 2007).
Up to now, it is little known about the mechanisms
of implicit sequence learning in SRNs. Using the ex-
ample of a biologically inspired classification task we
showed that the network’s learning performance de-
pends on the presence of a temporal order in the input
sequence (Gl¨uge et al., 2010).
In terms of the psychology of learning and biolog-
ical plausibility there is no doubt about the need for
models based on recurrent networks since biological
neural networks are recurrent. SRNs might be suit-
able to reproduce the data obtained from experiments
to study the effect of temporal order on associative
learning by humans (Hamid et al., 2010). Such model
should not just reproduce the data but also explain it
and further make verifiable predictions. Therefore,
one basic requirement is an understanding of the pro-
cesses in the network during learning/training.
In (Heskes and Kappen, 1991; Heskes and Kap-
pen, 1993) the learning process and the learning dy-
namics of neural networks were investigated from a
general point of view.
In this paper, the focus is not on the learn-
ing process in the SRN. But rather we investi-
gate how (implicitly learned) temporal information is
stored/represented in a SRN. Further, the influence of
the sequential input during training and testing is ex-
amined.
After training the network is tested on different
279
Glüge S., Böck R. and Wendemuth A..
IMPLICIT SEQUENCE LEARNING - A Case Study with a 4–2–4 Encoder Simple Recurrent Network.
DOI: 10.5220/0003061402790288
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
279-288
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)
input sequences under different conditions, e.g. with
and without working memory. To be able to study
detailed effects we use a small network and a standard
encoding task for this study.
2 THE 4–2–4 ENCODER SRN
Figure 1 shows a conceptual diagram of a SRN. Com-
pared to a feedforward network the SRN has an addi-
tional context layer. Each hidden unit is connected to
one corresponding context unit. The weights of these
recurrent connections are fixed to 1. Thereby, each
context unit stores a copy of the output of the cor-
responding hidden unit. At the next time step each
context unit feeds its copy back to all hidden layer
units. Due to the time delay and the feedback loop in
the information processing flow the network is able to
memorise earlier internal states. Therefore, the out-
put of the hidden layer depends on the actual input
and implicitly on input from all previous time steps.
Figure 1: Conceptual Diagram of a SRN.
2.1 Learning Task
The encoding task is the conversion of four 1−of−4
coded input vectors into a binary representation and
vice versa. For the network, the task is first to find
a mapping for the 1−of−4 coded input into a binary
code. The second part is the retrieval of the binary
coded input into a 1−of−4 coded output. Table 1
shows one possible solution for the problem.
Table 1: 4–2–4 encoding.
Input Binary Code Output
0001 00 0001
0010 01 0010
0100 10 0100
1000 11 1000
Attention should be paid to the fact that the encod-
ing is independent of the sequence of input vectors.
The network learns a direct mapping between input
and output. Nevertheless, we will see that the SRN
implicitly learns a temporal relation between inputs
and uses this as an advantage for memorising.
2.2 Network Configuration
If we denote y
(0)
(t), y
(1)
(t) and y
(2)
(t) as output vec-
tors of the input, hidden, and output layer at time t,
a
(l)
(t) with l = 1, 2 as network activation vectors of
the hidden and output layer, and w
(l,l
′
)
as weight ma-
trices between layer l and l
′
, the forward pass of the
4–2–4 encoder SRN (Fig. 2) with activation function
f can be written as:
a
(1)
i
(t) =
∑
j
w
(1,0)
ij
y
(0)
j
(t) +
∑
j
w
(1,1)
ij
y
(1)
j
(t −1), (1)
y
(1)
i
(t) = f (a
(1)
i
(t)), (2)
a
(2)
i
(t) =
∑
j
w
(2,1)
ij
y
(1)
j
(t), (3)
y
(2)
i
(t) = f (a
(2)
i
(t)) . (4)
Figure 2: 4–2–4 SRN.
The input layer consists of 4 input units which simply
excite or not, given the coding of the input vector. The
hidden layer has the hyperbolic tangent as activation
function. Hence, the output of the hidden layer is
y
i
(1)
(a
i
(1)
) = tanh(a
i
(1)
) . (5)
Each hidden layer unit is connected to one corre-
sponding unit in the context layer. The connection
weights are fixed to 1. The context units are fully con-
nected to the hidden layer providing it with the hidden
layer output from the previous time step. Four differ-
ent input vectors can be represented by two bit. Since
we want the network to code the input vectors into a
binary representation the number of units in the hid-
den layer is set to two. Furthermore, the two hidden
units are fully connected to four output units. This
corresponds to the retrieval of the binary coded input
into a 1−of−4 coded output. As the output units shall
generate values between 0 and 1 their activation func-
tion is the logistic function. The network output is
y
i
(2)
(a
i
(2)
) =
1
1+ e
−a
i
(2)
. (6)
Note that the hyperbolic tangent at the hidden layer
produces values between −1 and 1. The internal rep-
resentation for the input will consist of values in the
ICFC 2010 - International Conference on Fuzzy Computation
280

interval (−1, 1) and not of 0 and 1 as in Table 1. It
is still required that the internal representation be ’bi-
nary’ in the sense that the hidden layer has to produce
coding values for a uniquely distinguishable mapping
at the output layer. The input and output is presented
to the network as shown in Table 1.
The SRN can be seen as a feedforward network
with additional inputs from the context layer and any
algorithm for feedforward networks can be used to
train it (Elman, 1990).
2.3 Network Training
We use the backpropagation algorithm to train the
SRN. To do so, two constraints have to be fulfilled.
1. The context units must be initialised with some
activation for the forward propagation of the first
training vector. Commonly, these initial values
are zero.
2. The activation levels of the hidden layer must be
stored in the context layer after each back propa-
gation phase. Hence, the context layer shows the
state of the hidden layer delayed by one time step.
After each input the network output is compared to
the desired output and the mean square error is prop-
agated back through the network. The weights are
updated with the constant learning rate ε = 0.1. Since
each output is evaluated right away, the process cor-
responds to online learning.
The weights are initialised with uniformly dis-
tributed random values in the interval [−0.3, 0.3]
(apart from the fixed hidden–to–context layer
weights). The learning rate and weight initialisation
interval are chosen according to preliminary tests. We
use the combination that yielded best training results
after 1000 training cycles.
3 SIMULATIONS
The above described network was implemented in
Matlab. Since we are interested in the network’s abil-
ity in terms of implicit sequence learning we present
the training input in two different ways, a sequential
and a random one.
One training cycle consists of a presentation of all
four input vectors that are shown to the network one
after another. For the case of a deterministic order
the first cycle is repeated for the whole training. This
implies a strong temporal relationship between the in-
put vectors since each one has a fixed successor. For
the case of a random order in each cycle the temporal
correlation between the input vectors is very weak.
If we denote the input vectors with the numbers
from one to four we can describe the two types of
sequences as follows:
det. sequence . . . |
cycle n
z }| {
1 2 3 4 |
cycle n+1
z }| {
1 2 3 4|. . .
random sequence . . . |
cycle n
z }| {
4 3 1 2 |
cycle n+1
z }| {
2 1 3 4|. . .
The network is trained for 1000 cycles. Hence, every
input vector is shown 1000 times to the network. This
results in 4000 training steps or rather 4000 weight
updates.
3.1 Training
3.1.1 Success of the Training
To measure the success of the network we evaluate
the output according to the winner–take–all principle.
The unit with the highest activation is counted as 1 the
remaining as 0. Thus, the network’s output is always
mapped onto a corresponding target vector.
We evaluate the network output in terms of the
probability of success (P
S
) for each training cycle.
When training starts the probability to excite the cor-
rect output is one out of four (P
S
= 0.25). At the end
of training the network should have learned the cod-
ing and always deliver the target vector, therefore we
expect P
S
= 1.
Since the weights are initialised randomly the
learning curves for single networks may differ consid-
erably. As we want to compare the general behaviour
of the network we train 100 networks on each type
of input sequence. Afterwards we calculate the mean
probability of success over the 100 networks (P
S
) for
the two test cases. In Figure 3 P
S
is plotted against the
number of training cycles. In general, the networks
perform better on a deterministic input sequence than
on a random one. In both cases, however, the ex-
pected P
S
= 1 is not reached, which we will explain
in the following.
Figure 4 shows the distribution of P
S
for the 100 net-
works after training. We plot the number of networks
n against the final probability of success P
S
. Trained
with a deterministic sequence one half of the networks
(n = 51) learned the encoding completely (P
S
= 1 by
the end of the training). On the other hand, only 23
networks could succeed if trained with a random se-
quence.
In summary it is more likely that a network trained
with a deterministic sequence is able to learn the task
IMPLICIT SEQUENCE LEARNING - A Case Study with a 4-2-4 Encoder Simple Recurrent Network
281
200 400 600 800 1000
0
0.2
0.4
0.6
0.8
1
P
S
cycle
det. sequence
random sequence
Figure 3: Success of training for the deterministic and ran-
dom sequence.
0 0.25 0.5 0.75 1
0
20
40
60
80
P
S
n
det. sequence
random sequence
Figure 4: Distribution of final probability of success after
training of 100 nets.
in the training. The reason is the temporal correla-
tion between the input vectors. This extra informa-
tion, which is only provided in the deterministic se-
quence, raises the probability of the SRN to learn the
task.
3.1.2 Unstable Solutions and Training
Algorithm
Apparently, the learning task is quite demanding,
since a high percentage of the networks could not find
an optimal solution. Those networks that did not suc-
ceed in training learned an unstable solution.
Figure 5 exemplarily shows the activation of the
two hidden units during training for a network that
did not find a distinct encoding. Each input vector
is presented once per training cycle. We plotted the
activation of each hidden unit for one specific input.
The combination for the units’ activation represents
the network state and therefore, the coding of the in-
put vector. At the beginning of the training all inputs
are represented by activations around zero. At the end
of the training one can see that input vector 2 and 4
are well distinguishable while the inputs 1 and 3 re-
0 500 1000
−1
−0.5
0
0.5
1
0 500 1000
−0.5
0
0.5
1
0 500 1000
−1
−0.5
0
0.5
1
0 500 1000
−1
−0.5
0
0.5
1
cyclecycle
cyclecycle
units’ activation units’ activation
hidden layer: input vector 1 hidden layer: input vector 2
hidden layer: input vector 3
hidden layer: input vector 4
unit 1
unit 2
Figure 5: Hidden layer output during training for the four
inputs of a network that did not succeed in training.
sult in a nearly identical activation. The network did
not learn to distinguish these input vectors.
Table 2 shows the exact numerical values for the acti-
vations caused by each input vector at the end of the
training.
Table 2: Final hidden layer activations of a network that did
not succeed in training (input 1 and 3 hardly distinguish-
able).
Input Vector Unit 1 Unit 2
1 −0.8770 0.3435
2 0.9999 0.5431
3 −0.7429 0.2746
4 0.6793 −0.9983
It might be possible to avoid such unsuccessful train-
ing results by a more sophisticated training algorithm
(e.g. a variable learning rate, a better measure for
the network error etc.). Nevertheless, some networks
learned to solve the task with the simple learning al-
gorithm we used. Figure 6 shows the activation of the
two hidden units during training for a network that
found a distinct encoding. Again, we plotted the acti-
vation of each hidden unit for one specific input vec-
tor.
Table 3 shows the exact numerical values for the acti-
vations caused by each input at the end of the training.
Table 3: Final hidden layer activations of a network that
succeeded in training (all inputs distinguishable).
Input Vector Unit 1 Unit 2
1 0.2384 0.9794
2 −0.9999 0.9876
3 −0.9988 −0.9872
4 0.9993 −0.9068
Since we are only interested in the influence of the
temporal context in the input sequence and the role of
ICFC 2010 - International Conference on Fuzzy Computation
282
0 500 1000
−1
−0.5
0
0.5
1
0 500 1000
−1
−0.5
0
0.5
0 500 1000
−1
−0.5
0
0.5
1
0 500 1000
0
0.5
1
cycle
cyclecycle
cycle
units’ activation
units’ activation
hidden layer: input vector 1
hidden layer: input vector 2
hidden layer: input vector 3
hidden layer: input vector 4
unit 1
unit 2
Figure 6: Hidden layer output during training for the four
inputs of a network that succeeded in training.
the context layer we did not optimise the learning al-
gorithm. By that, we have the opportunity to compare
the results of the training while the only difference is
the sequence of training inputs. An optimal learning
algorithm for the given task is not in the focus of our
study.
3.1.3 Weights of the Context Layer
The success of the training shows that the networks
use the temporal relations of the input vectors. The
question is, how is this represented in the network?
The answer lies in the weights of the network since
this is the only parameter that is changed during train-
ing. Further, the key component to sequence learning
is the context layer, thus we investigate the develop-
ment of the weights of this layer.
Two context units are fully connected to two hid-
den units. This results in four weights in the context
weight matrix, w
(1,1)
ij
with i, j = {1, 2} (cf. Eq. 1).
Figure 7 exemplarily shows the weights of the con-
text layer during training. We plotted the four context
weights of two networks that solved the task (P
S
= 1
at the end of the training). Each training cycle con-
sists of four input vectors. A training of 1000 cycles
results in 4000 weight updates. The red lines show the
weights of a network trained with a random sequence.
The blue lines those of a network trained with a deter-
ministic sequence. Each line shows one weight of the
weight matrix.
For a deterministic sequence the weights take a value
between −2.5 and 2.5. Longer training would result
in higher weights, since the network tries to generate
exactly 1 at the output. This value is never reached
by the activation functions of the hidden and output
units.
The random sequence leads to vanishing context
weights. The network learns that there is no temporal
0 1000 2000 3000 4000
−2
−1
0
1
2
3
training step
weight
weights det. sequence
weights random sequence
Figure 7: Development of weights in context layer.
dependency in the input. This leads to the remarkable
result that the SRN turns into a standard feedforward
network and omits all context information.
3.2 Testing
For testing, we chose the networks that solved the task
at least in the last training cycle (P
S
= 1). As we will
see this criterion does not ensure that the solution the
network found is stable. We got 51 networks trained
with the deterministic sequence and 23 trained with
the random sequence for the test. The two sequence
types were presented to this networks again for 1000
cycles.
3.2.1 Test with the Deterministic Sequence
Networks Trained with the Deterministic Se-
quence should also produce comparable results
during testing. In our case 3 of the 51 networks per-
formed worse in the test run (P
S
= 0.25 or 0.5). An
analysis of these networks showed that two of them
did not learn a distinct encoding in the hidden layer.
In fact, the two networks did not provide a binary cod-
ing but a mixed coding or fuzzy coding which was
unstable.
The third had learned a clear encoding in the hid-
den layer but produced poor results in the test run.
Further investigation of the network showed that the
strange behaviour in the test run results from the miss-
ing context information at the initial test input. When
testing starts, the output of the context layer is set to
zero. Therefore, the first test input is processed at
the hidden layer without contextual information. This
gap in the flow of information from the context to the
hidden layer was sufficient to cause “confusion” in
the network which lead to the poor results. In other
words, the network based the decision, which input
vector to code, primarily on the context of an input
then on the input itself.
IMPLICIT SEQUENCE LEARNING - A Case Study with a 4-2-4 Encoder Simple Recurrent Network
283
The mean probability of success of the 51 net-
works during testing is constant P
S
= 0.9657.
Networks Trained with the Random Sequence
turned into feedforward networks by setting the con-
text weights to zero. The encoding is based solely on
the current input. Therefore, we expect that it does not
matter whether the networks are tested with a random
or deterministic sequence. In case of the random se-
quence 5 of the 23 networks showed an oscillating be-
haviour with a success rate between 75% and 100%.
Apparently the 5 outliers learned an unstable solution
during training. The remaining networks solved the
task in testing as in training to 100%.
The mean probability of success of the 23 net-
works during testing is constant P
S
= 0.9457.
3.2.2 Test with the Random Sequence
Networks Trained with the Deterministic Se-
quence did not learn just the input itself but also
the temporal correlation between inputs. Tested on a
random sequence this temporal information is miss-
ing. Further the temporal correlation that was learned
during training can be misleading. For instance if the
network learned that input vector 1 is followed by 2
but in the next step vector 3 is presented. Then the
network has to process two conflicting informations.
The input layer indicates vector 3 to the hidden layer
but the context at the present time–step indicats vector
2 to the hidden layer.
This results in a poor overall performance in the
test run. Figure 8 shows the mean probability of suc-
cess of the 51 networks during testing. The spiky
character of the curve can be explained with the fact
that parts of the random sequence may be equal to the
deterministic sequence.
Networks Trained with the Random Sequence
keep the high performance during testing. The mean
probability of success of the 23 networks during test-
ing is about P
S
≈0.95 (Fig. 8). This can be explained
by the pure feedforward processing of these networks.
The training with the random sequence turned them
into feedforward networks, thus the learned mapping
between input and output is independent of the tem-
poral context of the input.
3.2.3 Summary of the Test Results
Table 4 shows the mean probability of success of the
tested networks for the four combinations of training
and testing.
200 400 600 800 1000
0
0.2
0.4
0.6
0.8
1
P
S
cycle
networks trained with det. sequence
networks trained with random sequence
Figure 8: Probability of success during testing with the ran-
dom sequence.
Table 4: Results of Testing.
training
P
S
det. seq. random seq.
testing det. seq. 0.9657 0.9457
random seq. ≈0.5 ≈ 0.95
Networks tested with their training sequence unsur-
prisingly perform very well in the test run. Those who
did not succeed in the test learned an unstable solution
during training.
We saw that networks trained with the determin-
istic input sequence performed very poor in the test
with a random sequence. The networks learned the
coding based on the actual input plus contextual infor-
mation. The test result shows that this contextual in-
formation is not just some add on but absolutely nec-
essary for the networks to solve the new task. Since
the networks saw just one type of input sequence they
do not generalise to other types of sequences.
The networks that were trained with a random
sequence turned into feedforward networks during
training (cf. Sec. 3.1.3). Therefore, they could deal
with any kind of input sequence since the encoding of
an input is independent of the input sequence.
3.3 Test Without Context Layer
The result of the test run with the random sequence
shows that networks trained with the deterministic se-
quence heavily rely on the temporal structure of the
input. To investigate the influence of the context layer
we tested the networks again. This time we take
the trained networks and set their context weights to
zero. Thereby networks trained with a deterministic
sequence lose the previously learned temporal corre-
lation between input vectors.
Those networks trained with a random sequence
have zero context weights already thus, the replace-
ment by zero should have no effect to them.
ICFC 2010 - International Conference on Fuzzy Computation
284
We test the modified networks with the determin-
istic sequence for 1000 cycles. Table 5 shows the
mean probability of success in this test. The perfor-
mance of the networks trained with a deterministic
sequence drops dramatically while those trained with
a random sequence still perform very well (cf. Tab. 4).
Table 5: Results of Testing without context layer.
training
P
S
det. seq. random seq.
testing det. seq. 0.5196 0.9257
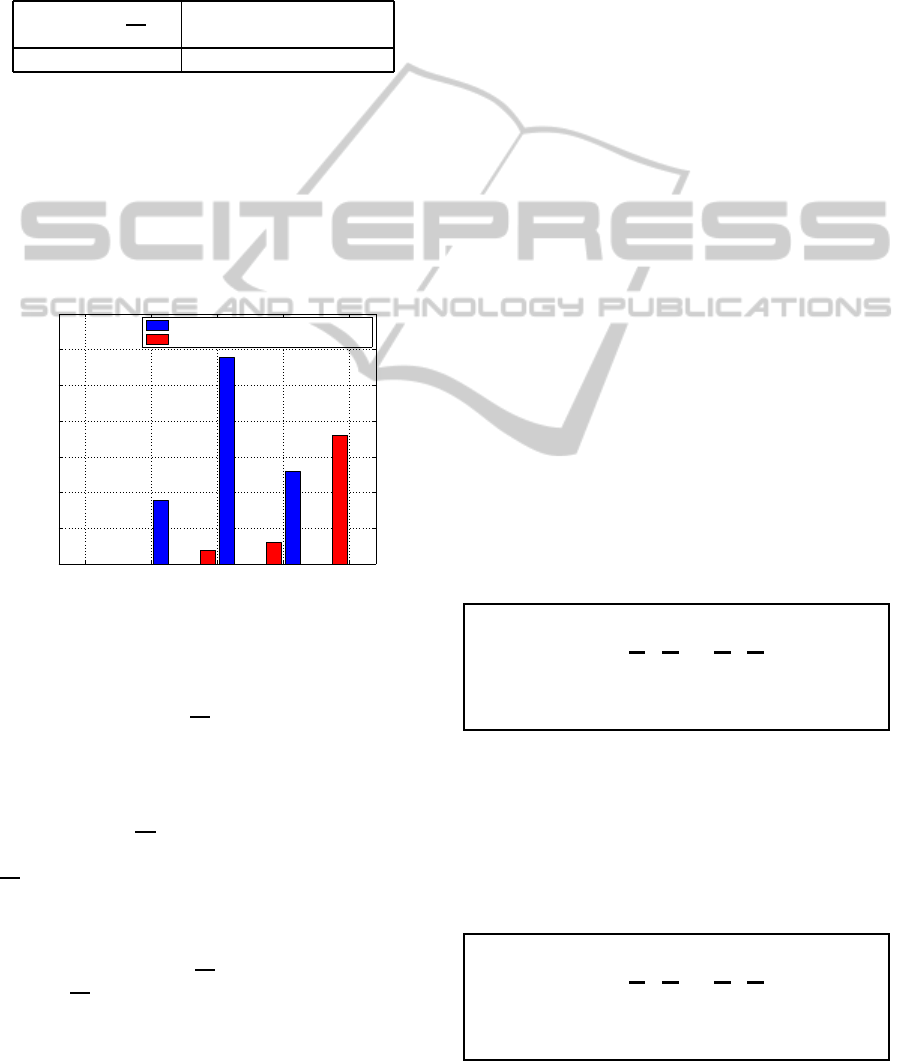
Figure 9 shows the distribution of P
S
for the 51 net-
works trained with the deterministic sequence. Not
all networks rely on the context layer to the same ex-
tend. The majority of the networks (n = 29) achieve
P
S
= 0.5 in the test run. For 13 networks the context
layer was less significant. They obtain a probability
of success above average, P
S
= 0.75. Further, 9 net-
works rely on the context layer to a greater extent and
therefore perform below average, P
S
= 0.25.
0 0.25 0.5 0.75 1
0
5
10
15
20
25
30
35
P
S
n
networks trained with det. sequence
networks trained with random sequence
Figure 9: Distribution of success for testing without context
layer.
The 23 networks trained with a random sequence
have zero context weights already. Their probability
of success remains high,
P
S
= 0.9239. Figure 9 shows
that 18 networks succeeded the test run. Another 5
networks achieved only a probability of success of
50% or 75%. This does not imply an importance of
the context layer to these networks. The mean prob-
ability of success P
S
= 0.9239 is comparable to those
achieved in the test with context layer in Section 3.2.1
(P
S
= 0.9457).
All in all, the test shows the relevance of the con-
text layer for networks trained with the deterministic
sequence. After removalof this layer the performance
in this test drops from P
S
= 0.9657 (with context
layer) to P
S
= 0.5196 (without context layer). Fur-
ther, Figure 9 points out that the influence of the con-
text layer may differ from network to network even if
the networks are trained in the same manner.
For networks trained with a random sequence the
context layer is of little importance as expected.
3.4 Output Sequences and their
Characteristics
3.4.1 Sequence Generation
Recurrent networks tend to oscillate, even if the input
is zero the networks produce an activation in the out-
put layer. Networks trained with a random sequence
do not oscillate since the feedback connections are
zero. We presented one initial input followed by ze-
ros for the duration of 1000 cycles and observed the
sequences that are generated. The networks trained
with a deterministic sequence produce a variety of
sequences. We observed four classes of sequences
after evaluation of the behaviour of the 51 networks
that succeeded the training with the deterministic se-
quence. The types of sequences are:
1. full cycle oscillation,
2. half cycle oscillation,
3. constant after transient oscillation,
4. others.
This distinction is not universally valid but seems to
be most adequate in terms of evaluation of the ob-
served data.
Full Cycle Oscillation (FCO): is a sequence that
reproduces the trained input sequence completely,
e.g. . . . |
cycle n
z }| {
1 2 3 4 |
cycle n+1
z }| {
1 2 3 4|. . . ,
or . . . | 2 3 4 1 | 2 3 4 1 |. . . .
In every cycle all four training inputs appear in the
order of the deterministic sequence (1, 2, 3, 4) but the
cycle does not necessarily start with “1”.
Half Cycle Oscillation (HCO): is a sequence that
reproduces some part of the trained input sequence
with the period of a half cycle,
e.g. . . . |
cycle n
z }| {
1 4 1 4 |
cycle n+1
z }| {
1 4 1 4|. . . ,
or . . . | 2 3 2 3 | 2 3 2 3 |. . . .
IMPLICIT SEQUENCE LEARNING - A Case Study with a 4-2-4 Encoder Simple Recurrent Network
285
Two input pattern appear alternating two times per cy-
cle.
Constant after Transient Oscillation (CTO): is a
sequence that takes a constant value after a transient
oscillation of about two cycles,
e.g.
cycle 1
z }| {
1 1 1 4 |
cycle 2
z }| {
2 2 2 2|
cycle 3
z }| {
2 2 2 2|. . . ,
or 4 3 4 3 | 4 3 4 3 |1 2 2 2 |. . . .
Others: are the sequences that do not fit into the
three classes above. For instance, sequences that re-
produce the trained input with a blemish or sequences
that produce an oscillation with a period that spans
over several cycles,
e.g. . . . |
cycle n
z }| {
1 3 3 4 |
cycle n+1
z }| {
1 3 3 4|
cycle n+2
z }| {
1 3 3 4|. . . ,
or . . . | 1 1 2 2 |2 3 3 3 |4 4 1 1 |. . . .
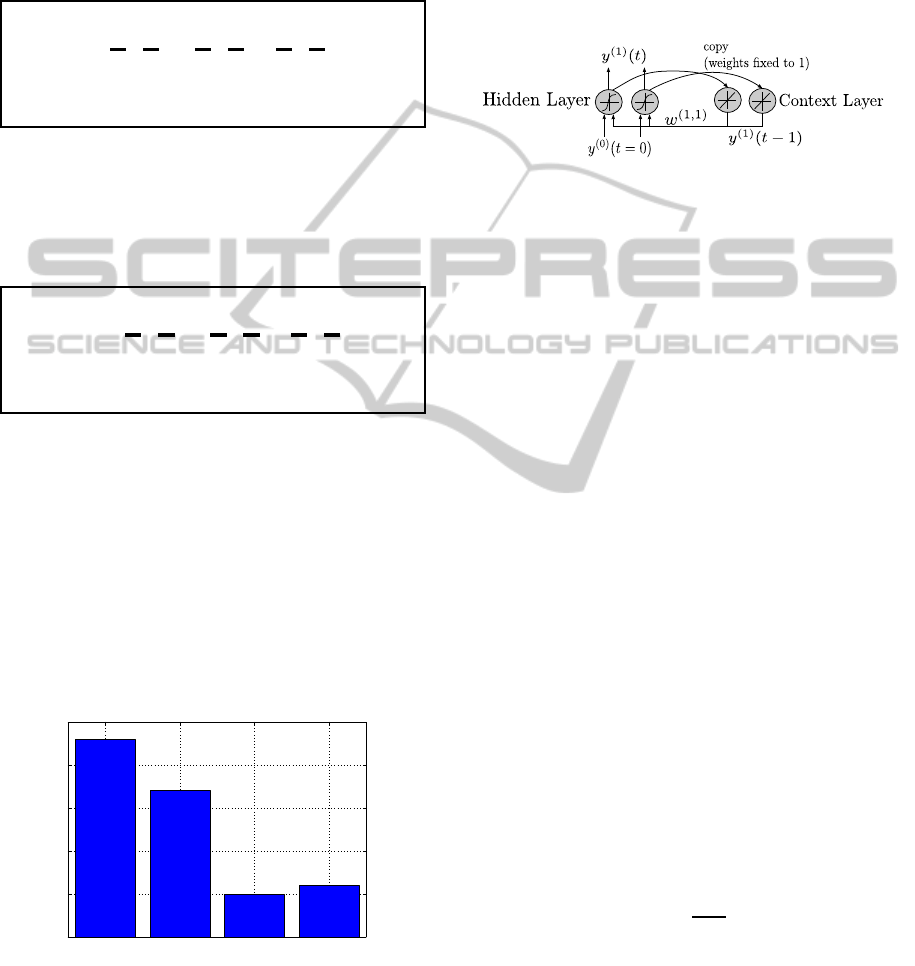
Figure 10 shows the distribution of the generated se-
quences over the classes of sequences. Most of the
networks (n = 23) generate the sequence presented
during training after activation with one single input
pattern. In terms of sequence learning these networks
performed best. Another group of networks (n = 17)
has an oscillating behaviour with the period of a half
cycle. This can be interpreted as a clock signal with
two pulses/beats per cycle. A constant output is pro-
duced by 5 networks after a short transient oscillation.
The remaining networks (n = 6) produced some oscil-
lation that does not fit into the aforementioned class.
FCO HCO CTO others
0
5
10
15
20
25
n
Figure 10: Distribution of sequences generated by 51 net-
works trained with deterministic sequence over classes of
sequences.
The key component to the generation of an oscilla-
tion by the network is the weight matrix of the context
layer. After one initial input, the input layer makes
no further contribution to the processing in the net-
work. The output layer provides the encoding from
the binary representation of the network state into the
1–of–4 coded representation at the output. The se-
quence of network states is solely generated by the
interplay of the hidden and context layer. Figure 11
shows the mentioned part of the SRN.
Figure 11: Interaction of Hidden and Context Layer.
The process of sequence generation can be described
by
y
(1)
1
(t) = tanh(w
(1,1)
11
y
(1)
1
(t −1) + w
(1,1)
12
y
(1)
2
(t −1)),
(7)
y
(1)
2
(t) = tanh(w
(1,1)
21
y
(1)
1
(t −1) + w
(1,1)
22
y
(1)
2
(t −1)),
with initialisation
y
(1)
i
(t = 0) = tanh(
∑
j
w
(1,0)
ij
y
(0)
j
(t = 0)). (8)
After the initial input, the network state y
(1)
(t) de-
pends only on the last state y
(1)
(t −1). The transition
of one state to another is controlled by the context
weight matrix w
(1,1)
. From this follows, that the prop-
erties of w
(1,1)
determine which sequence the network
generates or in other words, which sequence the net-
work learned during training.
3.4.2 Properties of the Context Matrix
By polar decomposition of a matrix it is possible to
separate the matrix into a component that stretches
the space along a set of orthogonal axes and a rota-
tion (Conway, 1990). The polar decomposition of a
complex matrix A has the form
A = RS (9)
where R is a unitary matrix and S is positive-
semidefinite. The matrix S represents the component
that stretches the space while R represents the rota-
tion. The matrix S is given by
S =
√
A
∗
A (10)
where A
∗
denotes the conjugate transpose of A. If A
is invertible, then the matrix R is given by
R = AS
−1
. (11)
We used the polar decomposition to extract some
properties of the context matrix that are related to the
generation of the specific types of sequences.
ICFC 2010 - International Conference on Fuzzy Computation
286

Full Cycle Oscillation. The component of the con-
text matrix w
(1,1)
that represents the rotation, takes
the form of a rotation matrix that acts as a rotation in
Euclidean space. For example
R
(1,1)
=
cos(Θ) −sin(Θ)
sin(Θ) cos(Θ)
. (12)
By that the generation of a sequence (7) turns into
y
(1)
1
(t) = tanh(R
(1,1)
11
y
(1)
1
(t −1) + R
(1,1)
12
y
(1)
2
(t −1)),
(13)
y
(1)
2
(t) = tanh(R
(1,1)
21
y
(1)
1
(t −1) + R
(1,1)
22
y
(1)
2
(t −1)),
which is a rotation of vector y
(1)
in the y
1
y
2
–plane
(counter)clockwise by an angle of Θ. This view
neglects the effect of the component of w
(1,1)
that
stretches the space. This is possible since the hyper-
bolic tangent always maps y
(1)
on values between −1
and 1. For the observed context matrices the angle Θ
lies between 78 and 100 degree. Figure 12 illustrates
the process of the sequence generation. At every time
Figure 12: Rotation of y
(1)
by the context matrix w
(1,1)
.
step the context matrix rotates y
(1)
into a newquadrant
where the hyperbolic tangent maps the single compo-
nents of the rotated vector onto the nearest 1 or −1.
By that y
(1)
passes all four quadrants and therefore
we observe all four training inputs at the output of the
network.
Half Cycle Oscillation. For networks that generate
a HCO the component of w
(1,1)
that represents the ro-
tation takes the form of a reflection matrix. A reflec-
tion matrix is orthogonal with determinant −1. The
eigenvalues are λ
1
= 1 and λ
2
= −1. In terms of a
geometric interpretation w
(1,1)
reflects y
(1)
from one
quadrant into another and reverse. Hence, y
(1)
passes
two quadrants and therefore, we observe only two of
the training inputs at the output of the network.
Constant after Transient Oscillation and Other.
For these types we found no property in the context
matrix that is shared by all observed matrices by now.
A deeper investigation of the relation between proper-
ties of the contextmatrix and these sequences remains
future work. Further the influence of the initial input
on the whole process needs to be analysed.
4 CONCLUSIONS
The learning task was constructed in a way such that
the sequential order of the input was not needed for
the solution. In this sense one can speak aboutimplicit
sequence learning, since the network was never ex-
plicitly trained to reproduce or predict the sequence.
During training (cf. Section 3.1) the sequential or-
der results in a higher learning performance. Nearly
twice as many networks learned the coding if trained
with a deterministic sequence than with a random one
(cf. Figure 4).
The observation of the weights in the context layer
shows the influence of this network layer in the pro-
cess of implicit sequence learning. A random input
sequence provides no sequential information and a
network trained with such input learns to reject the
information provided by the context layer. This re-
sults in vanishing context weights (cf. Figure 7). By
that the network turns into a standard feedforwardnet-
work.
The testing of the trained networks in Section 3.2
shows the importance of a previously learned sequen-
tial correlation between single inputs. The perfor-
mance of the networks trained with a deterministic
sequence heavily depends on the presence of the tem-
poral context in the input (cf. Figure 8 and Table 4).
The relevance of the context layer for the net-
works trained with the deterministic sequence was in-
vestigated by a test without this layer in Section 3.3.
The overall performance drops dramatically after this
change (cf. Table 4 and Table 5) but not all networks
rely on the context layer to the same extent (cf. Fig-
ure 9).
There is no sequence learning without a context
layer that provides the network with some memory.
On the other hand, there is no guarantee that the net-
work learns exactly the presented sequence in this
layer. In fact, the input sequence often can only be re-
produced in combination with an activation from the
input layer. Section 3.4 clearly shows this fact. The
variety of generated sequences (cf. Figure 10) points
out that the networks find different representations of
the sequential information. The context weight matrix
is the determining factor in this process.
IMPLICIT SEQUENCE LEARNING - A Case Study with a 4-2-4 Encoder Simple Recurrent Network
287

ACKNOWLEDGEMENTS
The authors acknowledge the support provided
by the federal state Sachsen-Anhalt with the
Graduiertenf¨orderung (LGFG scholarship).
REFERENCES
Cleeremans, A. (1993). Mechanisms of implicit learning:
connectionist models of sequence processing. MIT
Press, Cambridge, MA, USA.
Conway, J. (1990). A Course in Functional Analysis (Grad-
uate texts in mathematics). Springer.
Elman, J. L. (1990). Finding structure in time. Cognitive
Science, 14:179–211.
Gl¨uge, S., Hamid, O., and Wendemuth, A. (2010). Influence
of the temporal context on a simple recurrent network
in a classification task. In 7th International Sympo-
sium on Neural Networks (ISNN 2010).
Gupta, L. and McAvoy, M. (2000). Investigating the pre-
diction capabilities of the simple recurrent neural net-
work on real temporal sequences. Pattern Recogni-
tion, 33(12):2075 – 2081.
Hamid, O., Wendemuth, A., and Braun, J. (2010). Tempo-
ral context and conditional associative learning. BMC
Neuroscience, 11(1):45.
Heskes, T. M. and Kappen, B. (1991). Learning processes
in neural networks. Phys. Rev. A, 44(4):2718–2726.
Heskes, T. M. and Kappen, B. (1993). Mathematical ap-
proaches to neural networks, chapter On-line learn-
ing processes in artificial neural networks, pages 199–
233. Elsevier Science Publishers B. V.
Mandler, G. and Dean, P. J. (1969). Seriation: Development
of serial order in free recall. Journal of Experimental
Psychology, 81(2):207–215.
Reber, A. S. (1989). Implicit learning and tacit knowl-
edge. Journal of Experimental Psychology: General,
118(3):219–235.
Sluˇsn´y, S., Vidnerov´a, P., and Neruda, R. (2007). Behav-
ior emergence in autonomous robot control by means
of feedforward and recurrent neural networks. Pro-
ceedings of the World Congress on Engineering and
Computer Science 2007 WCECS 2007, October 24-
26, 2007, San Francisco, USA.
¨
Ubeyli, E. D. and
¨
Ubeyli, M. (2008). Recurrent Neural Net-
works, chapter Case Studies for Applications of El-
man Recurrent Neural Networks. InTech, Croatia.
ICFC 2010 - International Conference on Fuzzy Computation
288
