
PROBABILISTIC NEURAL NETWORKS FOR CREDIT RATING
MODELLING
Petr Hájek
Institute of System Engineering and Informatics, Faculty of Economics and Administration, University of Pardubice
Studenstká 84, Pardubice, Czech Republic
Keywords: Credit rating, Probabilistic neural networks.
Abstract: This paper presents the modelling possibilities of probabilistic neural networks to a complex real-world
problem, i.e. credit rating modelling. First, current approaches in credit rating modelling are introduced.
Then, probabilistic neural networks are designed to classify US companies and municipalities into rating
classes. The input variables are extracted from financial statements and statistical reports in line with
previous studies. These variables represent the inputs of probabilistic neural networks, while the rating
classes from Standard&Poor’s and Moody’s rating agencies stand for the outputs. Classification accuracies,
misclassification costs, and the contributions of input variables are studied for probabilistic neural networks
compared to other neural networks models. The results show that the rating classes assigned to bond issuers
can be classified accurately with probabilistic neural networks using a limited subset of input variables.
1 INTRODUCTION
Credit rating can be defined as an independent
evaluation in which the aim is to determine the
capability and willingness of an object to meet its
payable obligations. This is based specifically on
complex analysis of all the known risk factors of the
assessed object. The assessment is realized by a
rating agency. Credit rating is a result of a credit
rating process. It is represented by the j-th rating
class ω
j
Ω, Ω={AAA,AA, ... ,D}, where Ω is a
rating scale. The rating class ω
j
Ω is assigned to
assessed objects. Credit ratings are used by bond
investors, debt issuers, and governmental officers as
a measure of the risk of an object. Bankers and
companies considering providing credit rely on
credit ratings to make important investment
decisions. Credit ratings are costly to obtain due to
the large amount of time and human resources
invested by rating agencies to perform the credit
rating process. There is a great deal of effort made to
simulate the credit rating process of rating agencies
through statistical (Hwang and Cheng, 2008), and
artificial intelligence (AI) methods (e.g. Brennan
and Brabazon, 2004; Huang, Chen, Hsu, Chen and
Wu, 2004). The difficulty in designing such models
lies in the subjectivity of the credit rating process.
Such a complex process makes it difficult to classify
rating classes through statistical methods. However,
AI methods can be applied for the modelling of such
complex relations.
Probabilistic neural networks (PNNs) defined by
Specht (1990) are neural networks (NNs) for
classification which combines the computational
power and flexibility of NNs, while managing to
retain simplicity and transparency. So far PNNs
have been applied in only a few studies in finance
such as liquidity modelling (Li, Shue and Shiue,
2000) or audit reports qualifications (Gaganis,
Pasiouras and Doumpos, 2007). In this paper I will
demonstrate that they represent a suitable
architecture for credit rating modelling.
The paper is structured as follows. First, related
literature on corporate and municipal credit rating
modelling will be reviewed. Then, the basic notions
of PNNs will be presented. The models of PNNs
will be used for the modelling of corporate and
municipal credit rating. The input variables for the
modelling are designed based on all the aspects of
economic and financial performance of companies
and municipalities. Most input variables used in this
study have also been applied in previous works. In
this paper, however, financial market indicators have
been applied for the first time. An optimum set of
input variables will be obtained by using a
289
Hájek P..
PROBABILISTIC NEURAL NETWORKS FOR CREDIT RATING MODELLING.
DOI: 10.5220/0003062002890294
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
289-294
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

combination of correlation based approach (Hall,
1998) and genetic algorithms (GAs). The
contribution of input variables will be studied using
sensitivity analysis. Finally, the gained results will
be compared across selected models of NNs.
2 LITERATURE REVIEW
Recently, AI methods such as NNs (Brennan and
Brabazon, 2004; Moody and Utans, 1995), support
vector machines (SVMs) (Huang et al., 2004; Lee,
2007), artificial immune systems (Delahunty and
O’Callaghan, 2004), evolutionary algorithms
(Brabazon and O’Neill, 2006), and case based
reasoning (Lee, 2007) have been used for corporate
credit rating modelling. Usually, AI methods are
compared to statistical methods such as multiple
discriminant analysis (MDA) or linear regression
(LR).
As a result, high classification accuracy has been
achieved by NNs (Brennan and Brabazon, 2004) and
SVMs (Lee, 2007). Neural networks make it
possible to model complex relations as they learn the
dependencies in training data. The learnt knowledge
can also be applied for unknown input data which
were not used in the training process. Prior studies in
modelling credit rating were aimed at quantifying
the effect of input variables for classification, i.e. to
find out which input variables are crucial for credit
rating process. Mostly, sensitivity analysis has been
employed for this purpose.
Input variables are mostly represented by
financial ratios. Given the results of the previous
studies, it appears that the level of information
available in financial data is bounded (Brennan and
Brabazon, 2004). Although NNs are capable of
detecting non-linear structures in input data, it does
not appear that this has noticeably improved the
results, as the classification power of NNs is only
slightly better than that recorded by traditional
statistical methods. This suggests that additional
inputs are required to obtain significantly better
results. This is in line with the claims of rating
agencies who emphasise the importance of
qualitative factors in their rating decisions.
The specific position of municipalities associated
with their financial management, requires the use of
different input variables than for companies. Further,
municipalities have rarely financial resources to pay
for the credit rating. As a result, there has been less
attention paid to municipal credit rating modelling in
the literature. Small data sets make it difficult to get
consistent results. Therefore, conventional statistical
methods have been mostly used so far in the
modelling (Loviscek and Crowley, 2003).
There have been several attempts made to
overcome the problem concerning small municipal
data sets in the literature. One of the possibilities
consists in the design of an expert system based on
the knowledge acquired from the rating agencies’
experts (Olej and Hajek, 2007). Further, it is
possible to extend the training and testing set using
unsupervised methods (Hajek and Olej, 2008). In
this case only low proportion of municipalities are
labelled with rating classes ω
j
Ω a priori. The other
municipalities can be then labelled with the rating
classes ω
j
Ω belonging to the most similar labelled
municipality. Then it is possible to apply supervised
methods like NNs on such pre-processed data sets
(Hajek and Olej, 2008), or to use semi-supervised
methods (Hajek and Olej, 2009).
Except for the municipalities, credit ratings of
sub-national entities were also analyzed in the
literature. Ordered probit method was applied by
Gaillard (2009) for the modelling of non-US sub-
national credit ratings. The model explained more
than 80% of Moody’s sub-sovereign credit ratings.
3 PROBABILISTIC NEURAL
NETWORKS
Probabilistic neural networks are based on Bayes
classifiers. They learn to approximate the probability
density function of the training objects (i.e.
underlying objects’ distribution). They are regarded
as a special type of RBF NNs (Wasserman, 1993).
The PNN consists of neurons allocated in four
layers, Figure 1.
There is one neuron in the input layer for each
input variable. The pattern layer has one neuron for
each object in the training data set. The neuron
stores the values of the input variables for the object
along with the target value. When presented with the
x
i
, i=1,2, ... ,m, vector of input values from the input
layer, a pattern neuron k, k=1,2, ... ,n, computes the
Euclidean distance of the object x
i
from the neuron’s
centre x
k
, and then applies the RBF kernel function
using the sigma value. There is one neuron for each
class ω
j
Ω in the summation layer. The actual target
class of each training object is stored with each
neuron. The neurons add the values for the class
they represent. For an input vector x
i
, the output
f
j
(x
i
) of the summation layer is calculated in this
way:
ICFC 2010 - International Conference on Fuzzy Computation
290

jk
ω
ki,
j
ij
o
n
1
)(f
x
x
,
(1)
where n
j
is the number of training objects belonging
to the j-th class ω
j
and o
i,k
is the output of the
exponential activation function. Assuming that all
data vectors are normalized to unit length, the
following equation holds:
2
T
ik
ω
j
ij
σ
1
exp
n
1
)(f
jk
xx
x
x
.
(2)
Figure 1: Structure of a probabilistic neural network.
The decision layer compares the weighted votes
for each target class and uses the largest vote to
predict the target class ω
j
Ω. The outputs of the
summation neurons can be transformed to posterior
class membership probabilities:
q
1j
ij
ij
i
)(
f
)(
f
) jP(ω
x
x
x
.
(3)
Based on these probabilities, the j-th class ω
j
Ω,
for which P(j|
x
i
) is maximum, is assigned to the i-th
input vector
x
i
in the decision layer.
According to Specht (1990), the most obvious
advantage of the PNN is that training is trivial and
instantaneous. It can be used in real time because as
soon as one pattern representing each class has been
observed, the PNN can begin to generalize to new
patterns. As additional patterns are observed and
stored into the network, the generalization will
improve and the decision boundary can get more
complex. One of the disadvantages of the PNN
compared to the FFNNs is that PNN models are
large due to the fact that there is one neuron for each
pattern. This causes the model to run slower than
FFNNs when using it to predict classes for new
objects. Therefore, unnecessary neurons will be
removed from the model after the model is
constructed in this study. As a result, the size of the
stored model will be reduced, the time required to
apply the model for new patterns will be reduced,
and the classification accuracy of the model will be
improved.
4 DATASETS
Data for US companies and municipalities are used
for credit rating modelling. Datasets cover input
variables for 852 companies in the year 2007, and
for 169 municipalities in 2003-2007 (766 objects).
The companies are labelled with Standard&Poor’s
rating classes, while the municipalities are labelled
with Moody’s rating classes.
Rating agencies do not give publicity to their
credit rating factors. In the literature (Brennan and
Brabazon, 2004; Singleton and Surkan, 1995) the
main factors considered in assigning a rating class
ω
j
Ω to companies are company size, its character,
industry risk, and financial indicators. However,
some factors have either not been monitored yet
(industry, reputation), or so far only little attention
have been paid to them (asset management, market
value ratios). As there are plenty of corporate credit
rating input variables referred in the literature, the
design of the variables used in this paper contained
originally a set of 52 input variables drawn from the
Value Line Database and Standard&Poor’s database.
The original set of input variables was optimized
using correlation based approach and GAs so that
only significant input variables remained in the
datasets. For more information see Hall (1998). The
GA optimizes the set of input variables so that it
evaluates the worth of a subset of variables by
considering the individual predictive ability of each
variable along with the degree of redundancy
between them. The parameters of the GA are set as
follows: crossover probability=0.6, mutation
probability=0.03, population size=20, maximum
number of generations=20.
The obtained results show that the size of
companies is characterized by size class (SC) and
market capitalization (MC). Corporate reputation is
represented by the number of shares held by mutual
funds (IH). Profitability ratios are represented only
indirectly by ETR. Moreover, liquidity ratios are not
presented at all. The structure of assets (fixed
assets/total assets (FA/TA) and intangible
assets/total assets (IA/TA)) is related to industry
(sector). The input variable market debt/total capital
PROBABILISTIC NEURAL NETWORKS FOR CREDIT RATING MODELLING
291

(MD/TC) stands for leverage ratios. The rest of input
variables are associated with financial markets. Beta
coefficient and correlation of stock returns with
market index (Cor) show the relation between
corporate and market risk. The risk of stocks is
further represented by high/low stock price (HiLo),
while the dividend yield (Div/P) shows the return of
shareholders. The mean values for the input
variables show that the higher is the size of company
the better is the credit rating. On contrary, higher
debt and financial risk indicate worse credit rating.
The effect of other input variables is ambiguous.
Companies from manufacturing, services, and
transportation industries prevail in the dataset.
Frequencies of companies (f
comp
) and municipalities
(f
munic
) in rating classes are presented in Table 1.
Table 1: Frequencies of companies and municipalities in
rating classes.
ω
j
AAA AA A BBB BB B CCC CC D
f
com
p
7 26 129 261 233 164 18 2 4
ω
j
Aaa Aa A Baa
f
munic
60 241 436 29
Municipal credit rating is based on the analysis
of four categories of variables, namely: economic,
debt, financial, and administrative (Loviscek and
Crowley, 2003). Economic variables include socio-
economic conditions such as population,
unemployment, and local economy concentration.
Debt variables include the size and structure of the
debt. Financial variables inform about the scope of
budget implementation. Administrative factors
comprise of qualitative variables concerning
qualification of employees, municipal strategy, etc.
The original set of input variables included 14
variables. Again, this set was optimized by the GA
in order to obtain the final set of 3 significant input
variables, i.e. population (PO), median of family
income (FI), and the share of tax revenue on total
revenue (TAXR/TR). The values of the proposed
input variables were obtained for 169 US
municipalities (State of Connecticut) in years 2003-
2007. What becomes apparent from the mean values
of input variables is that municipalities with Aaa
rating class tend to be larger and in general in better
position either in terms of average family income
(FI) or fiscal autonomy (TAXR/TR).
5 EXPERIMENTAL RESULTS
Probabilistic neural networks are compared to other
benchmark classifiers, i.e. NNs (FFNN, SVM, RBF,
group method of data handling polynomial NN
(GHMD) and cascade correlation NN (CCNN)), and
statistical methods (LR, MDA). For all the methods,
10-fold cross-validation is used for testing. Thus,
overfitting is avoided. The average accuracies and
standard deviations for the given datasets are
reported in bold text in Table 1. Where a runner-up
does not differ at the 5% confidence level (using a
paired t-test), it too is recorded in bold. The
experiments were realized for different settings of
NNs’ parameters. The resulting settings of NNs’
parameters are as follows: PNN (Gaussian kernel
function), FFNN (m-1 neurons in the hidden layer,
logistic activation functions, learning rate of 0.05),
RBF (100 neurons in the hidden layer), SVM (RBF
kernel function), GHMD (quadratic function with
two variables), and CCNN (2 Gaussian neurons in
the hidden layer, 1 output neuron).
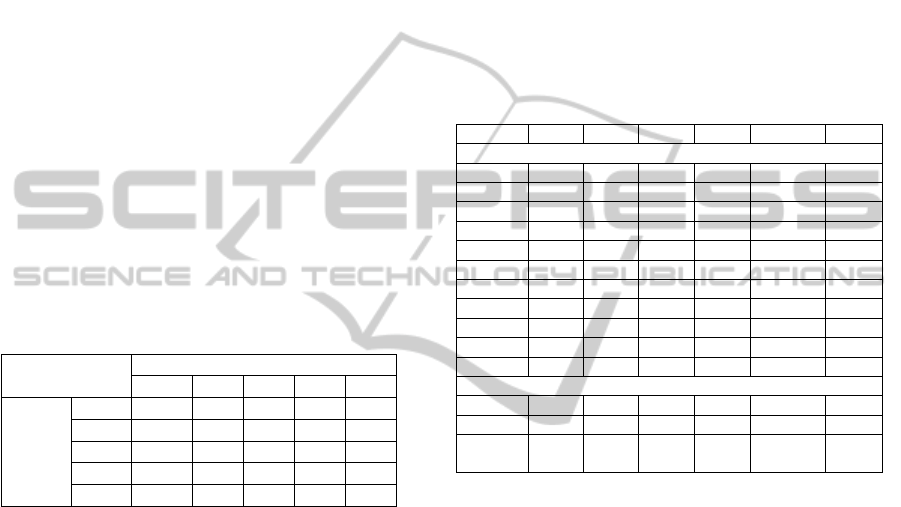
Table 2: Results of credit rating classification.
comp. munic.
Model
CA
test
±sd[%]
MC
test
±sd
CA
test
±sd[%]
MC
test
±sd
PNN
58.47±0.94 0.501±0.012 98.80±0.93 0.012±0.010
FFNN 51.71±2.24 0.525±0.023 86.30±1.68 0.144±0.021
RBF
58.28±3.08 0.489±0.025
92.80±1.88 0.072±0.019
SVM 55.63±1.52 0.551±0.012 96.00±2.16 0.045±0.021
GHMD 54.46±0.42 0.510±0.004 83.00±1.28 0.176±0.010
CCNN
57.69±2.16 0.503±0.018
91.10±1.76 0.092±0.019
MDA 55.83±1.32 0.554±0.009 78.60±3.35 0.226±0.031
LR 53.28±0.69 0.543±0.005 74.40±2.62 0.285±0.034
Legend: CA
test
is classification accuracy on testing data, MC
test
is
misclassification cost on testing data, sd is standard deviation.
For the corporate credit rating problem, PNN
shows best results concerning classification accuracy
(CA
test
=58.47%). Similar results are obtained also
for RBF and CCNN as classification accuracies of
higher than 57% were obtained. A considerably
worse classification was realized by the FFNN
model. The rating scale Ω with more than q=9 rating
classes was used only by Moody and Utans (1995)
with the classification accuracy of CA
test
=36.2% on
US data. Furthermore, in the case of six-class credit
rating problem, the classification accuracy of 66.7%
(Maher and Sen, 1997) was obtained.
For the municipal credit rating problem, the
highest classification accuracy CA
test
of 98.8% is
obtained using PNN. The comparison to prior
studies is possible to realize only with the MDA
method, as it was mostly used for municipal credit
rating modelling. For a three-class problem,
ICFC 2010 - International Conference on Fuzzy Computation
292
classification accuracy on testing data CA
test
was
66% (Serve, 2001) on European data, and 62% for a
four-class problem (Farnham and Cluff, 1982) on
US data. In this study the results obtained for the
four-class problem using statistical methods (78.6%
for MDA, 74.4% for LR) are slightly better than
previous results, while PNNs (98.8%) and SVMs
(96.0%) achieved significantly better classification
quality.
More accurate information on classification can
be presented using misclassification cost MC
test
which takes into account the fact that the rating
classes are ordered from the best one to the worst
one. The cost matrix for companies is designed in
Table 3. The greater the difference between actual
and predicted class is, the higher is the
misclassification cost. Accordingly, the cost matrix
is proposed also for municipalities. The results are
similar to those measured by classification
accuracies. For companies, RBF shows the least
misclassification cost (MC
test
=0.489), while PNN
outperforms other classification models in case of
municipalities.
Table 3: Misclassification cost matrix.
Rating class
Predicted
AAA AA A … D
Actual
AAA 0 1 2 … 8
AA 1 0 1 … 7
A 2 1 0 … 6
… … … … …
D 8 7 6 … 0
For a user, it is also important to get information
about the process of classification, i.e. how the NNs
obtain the results. The goal of the model’s
interpretation consists in the evaluation of input
variables’ effects on the results of classification. In
this study the calculation of variables’ importance is
performed using sensitivity analysis. The values of
each input variable are randomized and the effect on
the quality of the model (classification accuracy) is
measured. Finally the contributions of input
variables are standardized so that the contribution of
the most important input variable is 100%, and the
contributions of other input variables are related to
this variable. The resulting relative contributions of
input variables on corporate and municipal rating
classes are presented in Table 4.
For the nine-class corporate credit rating
problem, the size of the company is the most
important input variable (SC, MC). Further, the
input variables MD/TC and SIC play important
roles. As a result, I can declare that the size of
companies, their debt, and industry are the most
important factors in corporate credit rating process
realized by Standard&Poor’s rating agency.
However, there are several other factors including
asset management, shareholder structure,
profitability, and financial risks which serve for
improving credit rating evaluation process.
In the case of municipalities, the size of the
municipality represented by its population (PO), and
the wealth of its population (FI) show the highest
contribution. However, municipal financial
autonomy is also important in municipal credit
rating process.
Table 4: Relative contributions [%] of input variables.
PNN FFNN RBF SVM GMDH CCNN
comp.
SC 100.0 100.0 100.0 62.2 74.2 100.0
MC 23.4 48.8 23.0 100.0 100.0 51.7
FA/TA 10.0 55.1 10.8 19.6 3.1 13.9
IA/TA 1.5 35.0 10.8 25.2 1.0 5.3
IH 3.7 45.9 10.8 11.9 0.2 3.7
ETR 16.7 49.4 13.7 27.7 25.9 16.3
MD/TC 54.4 54.1 57.6 31.2 16.4 70.0
Beta 14.5 51.6 6.5 19.7 3.9 17.6
HiLo 10.1 59.8 21.6 17.1 11.1 27.6
Div/P 41.7 26.2 12.9 31 10.4 4.1
Cor 28.1 49.7 32.4 24.4 31.9 36.7
munic.
PO 10.0 100.0 100.0 100.0 100.0 100.0
FI 100.0 54.0 69.0 58.0 51.0 58.0
TAXR/
TR
5.0 51.0 33.0 70.0 49.0 70.0
6 CONCLUSIONS
The paper introduces the problem of municipal
credit rating process. The results of the prior studies
show that several crucial problems are involved with
credit rating modelling. First, data availability was a
critical point of concern in earlier studies. A
sufficient number of objects assessed by rating
agencies and, at the same time, the values of
important input variables must be available when
modelling credit rating. Without a large data set, the
use of these input variables is also limited. The next
point lies in the selection of input variables, as rating
agencies do not publish the details of their credit
rating process, which would emphasise the
subjectivity of the evaluation process. Further, the
appropriate method has to be applied in order to
model the complex relations among the input
variables.
In this paper PNNs are proposed in order to
realize the presented problems. Data were collected
PROBABILISTIC NEURAL NETWORKS FOR CREDIT RATING MODELLING
293

for US companies and municipalities. The assessed
objects were labelled by rating classes from rating
agencies. The selection of input variables was
realized as a two-step procedure. First, the original
sets of input variables were proposed based on
previous studies. Then correlation based approach
together with GA was employed with the aim of
reducing the original sets. The PNNs showed best
results for both the corporate and the municipal
credit rating problem. The results conform to prior
research results (Brennan and Brabazon, 2004;
Huang et al., 2004) indicating that the models of
NNs based on publicly available financial and
nonfinancial information could provide accurate
classifications of credit ratings. The sets of variables
identified in this study captured the most relevant
information for the credit rating decision.
In future research, the sets of input variables can
be extended in order to involve also the qualitative
factors of credit rating process. So far, these
variables have been either ignored or replaced with
alternative quantitative input variables.
REFERENCES
Brabazon, A. and O’Neill, M. (2006). Credit Classification
using Grammatical Evolution. Informatica, 30, 325-
335.
Brennan, D. and Brabazon, A. (2004). Corporate Bond
Rating using Neural Networks, In Arabnia, H.R. (Ed.),
Proceedings of the Conference on Artificial
Intelligence (pp. 161-167).
Delahunty, A. and O’Callaghan, D. (2004). Artificial
Immune Systems for the Prediction of Corporate
Failure and Classification of Corporate Bond Ratings.
Dublin: University College Dublin.
Farnham, P. G. and Cluff, G. S. (1982). Municipal Bond
Ratings: New Directions, New Results. Public
Finance Quarterly, 26, 427-455.
Gaganis, Ch., Pasiouras, F. and Doumpos, M. (2007).
Probabilistic Neural Networks for the Identification of
Qualified Audit Opinions. Expert Systems with
Applications, 32, 114-124.
Gaillard, N. (2009). The Determinants of Moody’s Sub-
Sovereign Ratings. International Research Journal of
Finance and Economics, 31, 194-209.
Hajek, P. and Olej, V. (2008). Municipal Creditworthiness
Modelling by Kohonen’s Self-Organizing Feature
Maps and Fuzzy Logic Neural Networks. In Kurkova,
V. (Ed.), Lecture Notes in Artificial Intelligence (pp.
533-542).
Hajek, P. and Olej, V. (2009). Municipal Creditworthiness
Modelling by Kernel Based Approaches with
Supervised and Semi-Supervised Learning. In Palmer-
Brown, D., Draganova, Ch., Pimenidis, E. and
Mouratidis, H. (Eds.), Communications in Computer
and Information Science (pp. 35-44).
Hall, M. A. (1998). Correlation-Based Feature Subset
Selection for Machine Learning. Hamilton: University
of Waikato.
Huang, Z., Chen, H., Hsu, Ch. J., Chen, W. H. and Wu, S.
(2004). Credit Rating Analysis with Support Vector
Machines and Neural Networks: A Market
Comparative Study. Decision Support Systems, 37,
543-558.
Hwang, R. Ch. and Cheng, K. F. (2008). On Multiple-
Class Prediction of Issuer Credit Ratings. Applied
Stochastic Models in Business and Industry, 5, 535-
550.
Lee, Y. Ch. (2007). Application of Support Vector
Machines to Corporate Credit Rating Prediction.
Expert Systems with Applications, 33, 67-74.
Li, S. T., Shue, L. Y. and Shiue, W. (2000). The
Development of a Decision Model for Liquidity
Analysis. Expert Systems with Applications, 19, 271-
278.
Loviscek, L. A. and Crowley, F. D. (2003). Municipal
Bond Ratings and Municipal Debt Management. New
York: Marcel Dekker.
Maher, J. J. and Sen, T. K. (1997). Predicting Bond
Ratings using Neural Networks: A Comparison with
Logistic Regression. Intelligent Systems in
Accounting, Finance and Management, 6, 59-72.
Moody, J. and Utans, J. (1995). Architecture Selection
Strategies for Neural Networks Application to
Corporate Bond Rating. In Refenes, A.N. (Ed.),
Neural Networks in the Capital Markets (pp. 277-
300).
Olej, V. and Hajek
, P. (2007). Hierarchical Structure of
Fuzzy Inference Systems Design for Municipal
Creditworthiness Modelling. WSEAS Transactions on
Systems and Control, 2, 162-169.
Serve, S. (2001). Assessment of Local Financial Risk: The
Determinants of the Rating of European Local
Authorities. Lugano: EFMA.
Singleton, J. C. and Surkan, A. J. (1995). Bond Rating
with Neural Networks. In Refenes, A.N. (Ed.), Neural
Networks in the Capital Markets (pp. 301-307).
Specht, D. F. (1990). Probabilistic Neural Networks.
Neural Networks, 3, 109-118.
Wasserman, P. D. (1993). Advanced Methods in Neural
Computing. John Wiley & Sons: VNR Press.
ICFC 2010 - International Conference on Fuzzy Computation
294
