MULTI-OBJECTIVE OPTIMIZATION OF BOTH PUMPING

ENERGY AND MAINTENANCE COSTS IN OIL PIPELINE

NETWORKS USING GENETIC ALGORITHMS

Ehsan Abbasi and Vahid Garousi

Software Quality Engineering Research Group, Department of Electrical and Computer Engineering

Schulich School of Engineering, University of Calgary, 2500 University Drive N.W. Calgary, Alberta, Canada

Keywords: Pump operation scheduling, Multi-objective genetic algorithm, Non-dominated sorting genetic algorithm,

Oil pipeline networks, Power optimization.

Abstract: This paper proposes an optimization model for the pipeline operation problem using a dual-objective non-

dominated sorting genetic algorithm (NSGA-II). One and foremost objective is to minimize pumping

energy costs. The second objective is to recognize the pipeline operators’ concern on pumps maintenance

costs by reducing the number of times pumps are turned on and off. This is commonly believed as a main

source of wear and tear on the pumps. The formulation of the problem is presented in detail and the model is

tested on a hypothetical case study (which is based on consultation with two industrial partners). The output

results are promising since they would give operators a better understanding of different optimal scenarios

on a “Pareto front”. Operators can visually assess several alternatives, and analyse the cost-effectiveness of

each scenario in terms of both objective functions.

1 INTRODUCTION

Oil is commonly transported using pipelines by the

propulsion from centrifugal pumps powered by

either electricity or gas. Pumps are located along the

pipelines at the approximate interval of 20 to 100

miles, depending on the geography and size of the

pipelines, and also capacity requirements. Finding

the optimal operation policy (regime) of oil pipelines

is challenging due to change prone energy cost

structures and complex hydraulic models that pose

distinct challenges to the optimization analysis

(Webb, 2007). The pipeline-operation optimization

problem is known as a mixed-integer non-linear

optimization problem due to constraints dictated by

pipelines non-linear hydraulic model (Lindell et al.,

1994).

Oil distribution systems consist of components

such as reservoirs, pipes, pump stations, and valves.

Pipes carry the fluid(s) from reservoirs to the

designated delivery points, e.g., refineries, or ports.

Pumps provide pressure needed to overcome gravity

and pipe friction. Valves are in charge of controlling

flows and pressures. The entire operation is

expensive, due to the fact that usually large masses

of fluid are to be pumped. However, significant

savings can be achieved through efficient energy

management, by matching pumping schedules with

time and shifting heavy pumping to periods with

cheap tariff rates (e.g., night time) (Webb, 2007).

The objective of a pumping optimization

problem is to provide the operator with the least-cost

operation policy for all pump stations in the pipeline

distribution system while maintaining the desired

delivery schedule. The operation policy for a set of

pumps is simply a schedule that indicates when a

particular (fixed-speed) pump or group of pumps

should be turned on or off over a specified period of

time, and the setting of the operating speed in case

of variable-speed pumps. The optimal policy

attempts to result in the lowest total operating cost

subject to a given set of boundary conditions and

system physical and operational constraints (Lindell

et al., 1994).

This paper proposes an optimization model based

on Non-dominated Sorting Genetic Algorithm

(NSGA-II) (Deb, 2001) for finding optimal pump

operation schedule. The two objective functions are:

(1) minimizing the cost of electric energy used by

pumps, and (2) minimizing the number of pump

on/off switching, which is a conventional surrogate

measure of pumps maintenance cost (Meetings mi-

153

Abbasi E. and Garousi V..

MULTI-OBJECTIVE OPTIMIZATION OF BOTH PUMPING ENERGY AND MAINTENANCE COSTS IN OIL PIPELINE NETWORKS USING GENETIC

ALGORITHMS.

DOI: 10.5220/0003063801530162

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 153-162

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

nutes, Spring and Fall 2009).

The final output of NSGA-II is a set of solutions

(known as a Pareto front or Pareto set) in which each

solution is better than the others in at least one of the

objective functions. The Pareto set could be used by

an operator to recognize the trade-offs of sacrificing

an objective in favour of another. For instance, in the

case of our problem, the operator can visually assess

the energy cost effectiveness obtained by several

extra pump switching. This way, he/she can make a

better decision on to whether toggle a pump status,

which causes wear on the unit, or operate the system

with a higher cost.

The remainder of the paper is outlined as

follows. Section 0 reviews the related works on the

problem of pump operation scheduling. The

mathematical definition of the objective functions

and constraints are thoroughly discussed in Section

0. Section 0 explains the basic concept of NSGA-II,

which is chosen as our solution methodology. The

model is applied to a hypothetical pipeline network

and the results are presented in Section 0. Sensitivity

analyses of the case study are discussed in Section 0.

Finally, Section 0 concludes the paper and discusses

some of our future works directions.

2 RELATED WORKS

The problem of pipeline operation optimization has

been a subject of study in three major areas: (1)

water distribution networks, (2) natural gas

transmission pipelines, and (3) oil products

transmission pipelines. Although each of these

networks has its own characteristics in terms of fluid

behaviour, contract terms, network size, structure

and elements, but the general idea that forms the

backbone of formulating these problems remains

similar.

In (Solanas and Montolio, 1987), dynamic

programming (DP) was used to evaluate the optimal

pumps operation scenario. However, for practical

distribution networks comprising more pump units

that should be evaluated in longer time frames,

application of dynamic programming (DP) needs

extensive computational resources due to the ‘curse

of dimensionality’. This problem limits the

application of all dynamic programming-based

techniques to large-sized networks.

Zessler and Shamir (Zessler and Shamir, 1989)

used the method of progressive optimality which is

an iterative DP. Jowitt and Germanopoulos has

proposed a method based on Linear Programming

(LP) in (Jowitt and Germanopoulos, 1992) and have

linearized the formulations. However, any

linearization of the formulations would lead to

linearization errors.

Lansey and Awumah have considered pump

switching as an additional constraint in their

optimization model in (Lansey and Awumah, 1994)

which accounts for the hardly-quantifiable

maintenance costs. They have adopted a two-level

approach which is compromised of a pre-

optimization level as well as the actual optimization

step.

Ulanicki et al. (Ulanicki et al., 2007) presented a

dynamic optimization approach to solve the optimal

pump scheduling problem. The model is claimed to

be faster than other existing approaches and follows

a two-stage approach in finding the solution.

Aligned with the trends of other optimization

problems, recent efforts are conducted to implement

the pump scheduling optimization using heuristic

and meta-heuristic approaches such as ant colony

(Ostfeld and Tubaltzev, 2008), particle swarm

(Wegley et al., 2000), or genetic algorithms (Ilich

and Simonovic, 1998).

In (Ostfeld and Tubaltzev, 2008), both design

and operation aspect of the pipeline system have

been modeled simultaneously in order to find the

optimal design of the network. In (Ilich and

Simonovic, 1998), a search within the feasible

region has been used which is claimed to improve

the efficiency in comparison with conventional

Genetic Algorithm (GA) method. The method has

been tested on a hypothetical network having five

serial pumps.

Zhang in (Zhang, 1999) couples GA with a

transient-hydraulic simulation model to generate and

evaluate trial pipe networks designs in search of an

optimal solution. The developed approach has been

applied to the New York City’s water supply

tunnels.

A great number of research works has also been

conducted for pipeline scheduling problem in the gas

pipelines sector. The problem was formulated with

GA and implemented in the Pascal programming

language by Goldberg in (Goldberg, 1987a) and

(Goldberg, 1987b). Wright and et al (Wright et al.,

1998) applied simulated annealing for finding the

optimum configuration and power settings for single

compressor problem as well as multiple compressors

arranged in series with constant pressure drops in the

segment. In (Betros et al., 2006), a genetic algorithm

is developed to optimize operation of gas pipeline

networks. Mora in (Mora, 2008) proposes a multi-

agent cooperative search technique to optimize the

operation of large and complex natural gas pipeline

ICEC 2010 - International Conference on Evolutionary Computation

154

networks.

Albeit oil pipeline stations are accounted as a

very important category of pipelines, but very few

research works have been devoted to this area. This

might be due to the fact that most of the research in

this area relates to corporate closed-source software

development projects which mostly do not appear in

publications and, ultimately prevents third parties

from analyzing or reusing the details of the solution

methods developed (SSI, Last Viewed: April 2010).

In (Veloso et al., 2004), a spreadsheet-based

computational tool was used to reduce the energy

consumption at each pumping station in oil

pipelines. Firstly, all possible pumping arrangements

are related to viable flow rates of the pipeline under

consideration. Then, a hydraulic simulator is used to

calculate the cost of each arrangement. All the cost

values are imported to a spreadsheet, which will be

used for selecting the minimum operation

arrangement by the operators as needed. This

method was applied to a 3 pipeline station network

and sounds memory and time intensive for larger

networks. Also, this “snap-shot” optimization

procedure does not guarantee that the set of pump

arrangements over a time period gives the minimum

cost. In (Abbasi and Garousi, 2010), a mixed-integer

linear formulation for finding optimal pump

operation schedule for oil pipelines is introduced.

The nonlinear equations have been linearized in

small operational flow rate ranges so that the

linearization errors are as marginal as possible. The

proposed formulation is capable of identifying the

most cost-effective solution to the linearized format

of the problem by giving the operation regime with

the lowest-cost energy consumption that satisfies the

mandatory operational and physical constraints

given a set of time-varying and quantity-varying

electricity tariffs. The formulation is then

implemented in the GAMS toolset and tested on a

hypothetical network.

This paper builds on top of the previous efforts

conducted in this area by considering multi-

objectives for the oil pipeline operation scheduling

problem which enables the operators to better

compare the cost effectiveness of the two objectives.

To the best of the authors’ knowledge, no existing

article has attempted considering these two

objectives at the same time.

3 MATHEMATICAL

FORMULATION

Implementation of any optimization problem calls

for a due assessment of the formulation constructing

the model. In this section, the pipeline operation

problem has been defined. The constraints and

objective functions of the problem have been

formulated and explained based on the relevant input

parameters and decision variables.

3.1 Problem Definition

The optimal operation of oil pipeline networks

involves selecting pumps’ operational schedules that

provide the least operational cost and also least

maintenance costs, while satisfying the system

constraints over a given finite time horizon. The key

components of the pump scheduling problem are

network hydraulics model, operational constraints,

and the objective functions.

3.2 Decision Variables

Depending on the system characteristics and time

window that the system is being modelled in, the

decision variables can vary in many forms. In the

case of this paper, the first set of decision variables

defined is the set of binary variables to indicate the

on/off status of the pumps at each time step.

The speed of the pump, in case of the variable-

speed pumps, is another decision variable.

3.3 The Two Objective Functions

The first objective function is to minimize the total

cost of electricity used by pumps in the whole

operation period. The second objective function is to

minimize the number of pumps switching (on to off,

or off to on) (Lindell et al., 1994). Each of these

objective functions is discussed and formulated next.

3.3.1 Objective Function 1: Minimization of

Total Electricity Cost used by Pumps

The most important objective function of the

pipeline operation scheduling problem represents the

total operating cost to be minimized. It is usually

comprised of energy cost for all of the pump units in

the whole operation period. Although other costs

such as penalties for deviation from the final

delivery contract might be considered, in this paper

the delivery contract has been considered as an

operational constraint of the system.

Pumping cost is evaluated based on the

electricity power tariff over the pumping duration.

Two types of electricity charging patterns are

usually used in the industry (Prindle, Last Viewed:

MULTI-OBJECTIVE OPTIMIZATION OF BOTH PUMPING ENERGY AND MAINTENANCE COSTS IN OIL

PIPELINE NETWORKS USING GENETIC ALGORITHMS

155

April 2010):

 fixed electricity price rate;

 time-variable or quantity-variable electricity

price rate;

Due to the fact that the latter case is more

general, this pricing pattern has been considered in

this paper.

Also, it has to be noted that the oil pipelines are

usually expanded over a reasonable geographical

area, and they usually enter into contracts with

several local electricity providers for their electricity

needs. In this context, oil pipeline operators face

various electricity purchasing contracts. Some

companies offer incentive prices for electricity usage

to sell more electricity while, on the other hand,

some others encourage their customers to consume

less electricity (Meetings minutes, Spring and Fall

2009).

Some utilities encourage customers to limit their

consumption within a specific limit. Although any

nonlinear function of the consumed power and cost

is possible to be considered in GA models; however,

in this paper, it is considered that rate of electricity

follows the trend presented in Figure 1, which is a

generic case.

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.1

0 500 1000 1500 2000

ElectricityRate[$/kWh]

Power[kW]

Figure 1: Electricity Rates.

Power system companies are interested to have a

smooth load profile. This helps them in better

planning and scheduling of the power plants

operation to generate electricity by their highest

efficiency and also making use of the existing

transmission network close to nominal limit. Due to

these facts, usually power system providers consider

lower rates for the hours of the day that other

industrial sectors are off and lower consumption of

electricity is expected, which usually happens to be

around midnight.

In the case study reported in this paper, by

reviewing some example power contracts from our

industrial partner, it is assumed that the electricity

rate of daytime is twice the nighttime rate. It is

noteworthy that using genetic algorithm or any other

evolutionary algorithm as the solution technique,

any multiple segments and any type of cost

evaluation method could be modeled. Even any

nonlinear relationship between the electricity cost

rate and power consumption could be considered.

This is a significant feature of genetic algorithms

compared to more systematic approaches (e.g., LP,

MILP) on solving this problem which stems from

the flexibility of evolutionary algorithms in general.

Based on the aforementioned formulations, the

pumping cost objective function could be stated in

mathematical terms as:

















PCost

)(min

(1)

In which, P

is the power consumed by pump j at

time step t and is a function of pumps pressure, flow

rate passing, its operating efficiency and the fluids

characteristic which is constant. Note that the full

list of mathematical notations defined and used in

this article can be found at the end of this article.

The following equation calculates the power

needed to operate the pump (Boulos et al., 2006):

PHQ









(2)

In the above equation, the terms flow, pressure

and efficiency are not independent. Technicians

usually consult empirically driven curves to find out

the operating status of a specific point. However, in

order to formulate the problem, an explicit

relationship between power and the other variables

is needed.

According to experiments conducted by

mechanical engineers (Boulos et al., 2006), the

power consumption of a pump could be determined

as a function of two independent variables of

pump’s speed and the flow rate of the fluid passing

by it. According to (Ulanicki et al., 2008), a

polynomial equation as stated in Equation (3) best

fits the empirically-extracted pump curves.

32 23t t tt tt t

ijjjjjjjjjj

aQ bQ scQ s ds    

(3)

3.3.2 Objective Function 2: Minimization of

the Number of Pump State Changes

Another important cost issue that deserves conside-

ICEC 2010 - International Conference on Evolutionary Computation

156

ration is pump maintenance. An operation schedule

in which pumps are turned on and off very

frequently may reduce energy consumption;

however, this schedule may increase the wear and

tear on the pumps and increase the resulting pump

maintenance costs. It would also complicate the

operation of the system from the operator’s point of

view, i.e., the human operator has to constantly

review the operation schedule and turn the pumps on

and off. This task itself can be error prone and also

risky from system stability point of view.

The exact amount of maintenance costs is not

easily quantifiable, but it can be assumed that it

increases as the number of pump change status

increases. Hence, the number of pump change status

is used as a surrogate measure for the intangible

wear-and-tear maintenance costs. Therefore, the

switching objective is introduced into the model as

the second objective function. The operators can

then evaluate the trade-off of increasing cost to

reduce the number of switching by assessing the

model results.

This second objective function is formulated as

the following:

























BpBp

min

(4)

In which, the absolute difference between the

binary variables associated with the status of a

specific pump in two successive time intervals is

summed up over the entire time horizon and for all

the pump units. The final result is the number of all

pumps status changes seen in the analysis period.

3.4 Constraints

The search space for pipeline scheduling problem, as

mentioned earlier, is confined by a number of

constraints. Based on the technical aspects, these

constraints can be divided into two categories: (1)

hydraulics constraints, and (2) operational

constraints.

The hydraulic-model constraints stem from

natural behaviour of a fluid being transported in a

pipeline. These constraints validate the feasibility of

the model in sense of the relationship between the

primary state variables of the hydraulic model.

On the other hand, the operational constraints

account for the tolerance of the equipments or in

concise, their operation limits, as well as the

constraints imposed by contracts or any other

external cause.

The mathematical equations representing the afo-

rementioned constrains are being discussed in the

next sub-sections.

3.4.1 Hydraulic Constraints

When assessing a particular pump-operating policy,

it is essential to make sure that the hydraulic state

variables of the model match their natural

connection couched in mathematical equations. Any

fluid movement in a pipeline network entails

satisfying the two fundamental laws of conservation

of mass and conservation of momentum (Mennon,

2005).

The conservation of mass law for non-

compressible fluids, as the name implies, states that

a balance exists between the summation of the

masses entering and exiting at any point on the

pipeline at a specific time instance. Equation (5):

tiQQ

Outi

Ini



(5)

The conservation of momentum which is based

on the conservation of energy law, establishes a

relationship between the pressure generation and

losses in the pipeline. For any two successive

pressure points, the differences in absolute head

(pressure) is equal to the net head added to the

system by pumps (if there’s any) minus the head lost

in either valves or segment’s friction loss due to the

movement of the fluid.

Difference in the altitude of the according

locations also contributes to the equation as static

heads. Equation (6) indicates the conservation of

momentum law (Mennon, 2005).











tt tt ttt

qq pp jjj

HS H HS PH PL V j t

p q nodes being connected by segment j

 



(6)

The term PL

is the pressure loss that occurs in

pipeline segment j at time instant t as a result of

friction which depends on the fluid type, pipeline

material and cross section, and the flow rate passing

the segment. This loss could be quantitatively

evaluated by the Darcy-Weisbach equation (Tullis,

1989) as follows:





tjQCLPL



(7)

Since valves control high pressures, they appear

in Equation (6) accompanied by negative sign. The

last term of the Equation (6), PH

, represents the

pressure head added to the system by the pump

located on segment j at time t. The pumps head is a

function of the flow rate and also the speed of the

pump in case of variable speed pumps. The head-

MULTI-OBJECTIVE OPTIMIZATION OF BOTH PUMPING ENERGY AND MAINTENANCE COSTS IN OIL

PIPELINE NETWORKS USING GENETIC ALGORITHMS

157

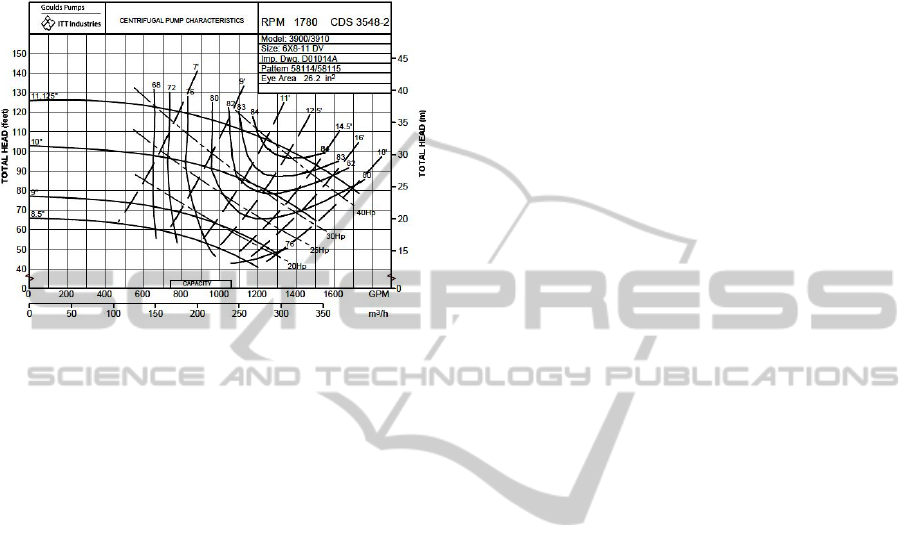
flow rate characteristic curve of a variable speed

pump is usually provided by the manufacturer for a

specific speed. A typical head/efficiency versus flow

rate curve of a variable-speed pump is presented in

Figure 2.

Figure 2: A typical head/efficiency versus flow rate curve.

Taken from (Goulds Pumps, Last Viewed: March 2010).

The head versus flow rate curve is often

approximated by a quadratic polynomial (Ulanicki et

al., 2008) as:

tt ttt

j j j j jj jj

HAPQBPQSCPS jt 

(6)

3.4.2 Operational Constraints

Beside the basic hydraulic constraints that lay the

groundwork for implementing the model, a

multitude of operational constraints exist to propel

the solution towards an operational range. These

constraints generally originate from equipments’

operation limitations. Also, contract-related

constraints or environment-related constraints are

considered to fall in this category.

The pipeline wall is prone to cracks and leaks if

it is operated under high pressures. This not only

causes serious damages to the pipe but also, flow of

oil products to the environment causing

environmental damages which is followed by

considerable penalties. Hence, it is essential that the

operators keep the pressure of the nodes especially

on junctions lower than a threshold. On the other

hand, low pressure in the pipeline causes formation

of cavities in the fluid which causes corrosions on

the pipeline wall. More severely, these cavities form

a two phase flow, which seriously damages the

impellers of centrifugal pumps. The two mentioned

constraints are expressed in Equation (7).

tiHHH

Max

min



(7)

Furthermore, the flow rate of the pipeline should

be bound to a certain limit, for high flow rates’

friction with pipeline wall causes overheat of the

pipe and product. This constraint is indicated by

Equation (8).

tjQQ

Max

,0 

(8)

The speed of rotation of the pump units are

bounded by an upper and lower limit as stated by the

following equation:

tjBSSBS

Max

min



(9)

Note that the binary variable B

sandwiches the

upper and lower bounds to zero at the times the

pump is off.

Finally, delivery contract imposes the most

prominent constraint on the problem. The pipeline

operator is supposed to deliver a contracted volume

of the product to the designated delivery points by

the end of the planning time period. Hence, the

summation of the volume of the fluid being

delivered to specified locations in every time step

should be more than or equal to the contracted

amount for that specific location. The corresponding

equation to this constraint is as follows:

iConQSink





1

(10)

4 SOLUTION METHODOLOGY

The Fast Non-dominated Sorting Genetic Algorithm

(NSGA-II) is a very popular approach in MOGA, as

it has been used in many existing works such as

(Kang et al., 2009) and (Baran et al., 2005). Thus, it

was also chosen to be used in this work. Efficient

sorting and ability to maintain a diverse set of elite

population could be counted as features of NSGA-II

(Deb, 2001).

5 CASE STUDY

To evaluate our optimization technique, we are

working with a Western Canadian oil pipeline

operator to apply our optimization technique to its

pipeline network. However, as of this writing,

extraction of actual parameters to be able to execute

the algorithm has not been completed yet.

In the mean-time, we evaluate the proposed ap-

proach on a hypothetical oil distribution system

comprising of 5 pipeline segments which connect 6

ICEC 2010 - International Conference on Evolutionary Computation

158

nodes. The system is designed to feed two delivery

nodes from a single source on a dendritic structure.

All of the segments are equipped with pump units

and valves. Structure of the network is shown in

Figure 3. It has been assumed that the whole

assessment timeframe is one day comprising three

time-of-use electricity tariffs, in which the cost of

the last time period is half of the cost of the other

two. The parameters of this hypothetical test system

could be found in the Table 1. The formulation of

this hypothetical system results in 62 decision

variables and 48 constraints.

Figure 3: Configuration of the test case pipeline network.

It should be noted that the formulation structure

is generic and any number of sources and delivery

points and also branches could be considered easily.

Table 1: Parameters of the hypothetical test system.

0.3

min

0.2

Con

i=4,5

Max

2.5

min

300

2.3×10

-6

Max

1000

8.3

Max

100

4.6×10

-3

7.4×10

-3

5.7×10

-7

1.66

3.6×10

-3

Electricity Rate 1 0.08

Electricity Rate 2 0.06 Electricity Rate 3 0.09

Change Rate

Value 1

1000

Change Rate

Value 2

1500

In order to investigate the ability of NSGA-II

dealing with pipeline operation optimization

problem, a MATLAB program was developed. The

GA parameters set for the algorithm is presented in

Table 2. These parameters were empirically

calibrated and were found as suitable parameters

after a series of experimental runs, using ideas from

the work of (Garousi, 2008).

By running the MATLAB program in MATLAB

version 2009a, the Pareto front depicted in Figure 4

was generated. Due to the random effects of GA, we

executed the MATLAB program for 50 times and

the average execution time of each run on a PC with

Windows Vista, a 2.30 GHz CPU, and 2 GB of

RAM was 885.36 seconds (about 15 minutes).

As it could be seen from the Pareto, higher cost

of operation comes with zero switching while the

case with three switching is the operation scenario

with the lowest cost. Noteworthy, the amount of

operation cost reduction is reasonable between

having one switching and no switching state. Also,

this amount is not negligible between having one

switching and two switching while no reasonable

cost reduction is achieved for the case of three pump

switching. Pipeline operators can make decisions

based on such Pareto to visually identify the trade-

offs of operations with low costs.

Table 2: Calibration of GA parameters.

Parameter Value

Population size 315

Number of Generations 100

Crossover Rate 80%

Mutation selection strategy Gaussian

164

166

168

170

172

174

176

178

180

0123

OperationCost[$]

X1000

PumpSwitching

Figure 4: Four solutions on the optimal Pareto-front of the

test case problem.

Table 3 and 4 present detailed output data

(decision variables) for two of the four pump

operation regimes. It should be noted that the

pressure reduction by valves of the network are

managed to be zero in all combinations. The first

pump is always running in order to add enough

pressure to compensate for the loss of the first line

segment. Similarly the second pump is always ON to

add enough pressure for the fluid to pass through the

pipeline.

MULTI-OBJECTIVE OPTIMIZATION OF BOTH PUMPING ENERGY AND MAINTENANCE COSTS IN OIL

PIPELINE NETWORKS USING GENETIC ALGORITHMS

159

Table 3: The pump operation schedule (speed values) for

zero switching.

Pump Period 1 Period 2 Period 3

1 2.4 2.4 2.4

2 1.7 1.7 1.7

3 0 0 0

4 0 0 0

5 0 0 0

* Operation Cost = $179,110.00

Table 4: The pump operation schedule (speed values) for

one switching.

Pump Period 1 Period 2 Period 3

1 2.4 2.4 2.4

2 0.9 0.9 0.77

3 0 0 0.43

4 0 0 0

5 0 0 0

* Operation Cost = $166,500.00

6 SENSITIVITY ANALYSIS

In order to assess the effect of variation of GA

parameters on the performance of the model, several

sensitivity analyses were conducted, as discussed

next.

6.1 Population Size

The population size of the solutions has been

changed from 10 to 500 in the increments of 50. The

optimization results for the amount of cost for the

second objective of 3 switching have been presented

in Figure 5.

As it could be seen from Figure 5, the more the

size of the population grows, less improvement in

the cost is seen due to the fact that the GA results get

closer to the global optimum which may not be

improved then after. Hence, the effect of population

growth beyond 400is more or less subtle.

Expectedly, the execution time increases

dramatically as population size is incremented. The

variation of execution time versus the population

size is presented in Figure 6. Inspecting Figure 5 and

Figure 6 simultaneously, it is clear that any

increment in population size after the margin of 300

causes slight improvement in operation cost but with

tremendous increase in execution time. For instance,

shifting from population size of 300 to 900 leads to

0.04% improve in operation cost of the solution with

three switching but the execution time of 900

population is approximately 84.4 times longer than

that of 300. This poses another factor in selecting the

right population size for the algorithm which is the

trade-off in cost improvement and the raise in

execution time.

164.8

164.9

165

165.1

165.2

165.3

165.4

165.5

0 200 400 600 800 1000

OperationCost[$]

X1000

PopulationSize

Figure 5: Decrease in cost of operation versus increase in

GA’s population size setting.

0 200 400 600 800 1000

ExeutionTime[hours]

PopulationSize

Figure 6: Execution time versus population size.

6.2 Crossover Rate

Figure 7 depicts the variation of the cost of operation

of three switching for different values of the GA

crossover rate. This empirical analysis justifies the

choice of the crossover rate of 80% since the best

result is achieved at this point.

164.95

165

165.05

165.1

165.15

165.2

165.25

0 0.2 0.4 0.6 0.8 1

OperationCost[$]

X1000

CrossoverRate

Figure 7: Minimal cost of operation found for 3 switching

versus crossover rate.

ICEC 2010 - International Conference on Evolutionary Computation

160

7 CONCLUSIONS AND FUTURE

WORKS

In this work, an optimization model was developed

for minimizing the costs of pumping while satisfying

fluid flowing and hydraulic constraints. Several

major difficulties including complicated electrical

tariffs, wear and tear of the pipelines has been

implicitly considered. Multi-objective genetic

algorithm was chosen as the optimization technique.

This technique can help the operators to choose the

appropriate operating point based on their

experience and unformulated priorities considering

both objective functions values. The numerical

results indicate the viability and applicability of the

model.

As future work directions, we plan to work with

our industrial partner, Pembina Pipelines, a Western

Canadian oil pipeline operator, to apply our

technique to their pipeline networks and to optimize

their operational costs. Also, we intend to make use

of the flexibility of GA to formulate the multi-

products pipelines operation. This problem is

challenging due to the fact that the movement of

various liquids that are being transported

simultaneously by the pipeline should be modelled

over the time span.

ACKNOWLEDGEMENTS

This work was supported by the Alberta Ingenuity

New Faculty Award grant number 200600673. We

would like to thank Pembina Pipeline Corporation

for its collaborations in this project.

REFERENCES

Abbasi, E. & Garousi, V. (2010) Decreasing The Carbon

Footprint Of Oil Pipelines By Minimizing Pumping

Costs Using Milp. Informs Optimization Society

Conference On Energy, Sustainability And Climate

Change (Cescc). Gainesville, Florida, Usa.

Baran, B., Lucken, C. & Sotelo, A. (2005) Multi-

Objective Pump Scheduling Optimizatoin Using

Evolutionary Strategies. Advances In Engineering

Software, 36, 39-47.

Betros, K. K., Sennhauser, D., Jungowski, J. & Golshan,

H. (2006) Large Pipeline Networks Optimization -

Summary And Conclusion Of Transcanada Research

Effort. International Pipeline Conference. Calgary,

Canada, Asme.

Boulos, P. F., Lansey, K. E. & Karney, B. W. (2006)

Comprehensive Water Distribution Systems Analysis

Handbook For Engineers And Planners, Pasadena,

California, Mwh Soft.

Deb, K. (2001) Multi-Objective Optimization Using

Evolutionary Algorithm, New York, Ny, Usa, John

Wiley & Sons Inc.

Garousi, V. (2008) Empirical Analysis Of A Genetic

Algorithm-Based Stress Test Technique For

Distributed Real-Time Systems. Genetic And

Evolutionary Computation Conference (Gecco).

Atlanta, Georgia, Usa.

Goldberg, D. E. (1987a) Computer-Aided Pipeline

Operation Using Genetic Algorithms And Rule

Learning. Part I: Genetic Algorithms In Pipeline

Optimization. Engineering With Computers, 3, 35-45.

Goldberg, D. E. (1987b) Computer-Aided Pipeline

Operation Using Genetic Algorithms And Rule

Learning. Part Ii: Rule Learning Control of A Pipeline

Under Normal and Abnormal Conditions. Engineering

With Computers, 3, 47-58.

Goulds Pumps (Last Viewed: March 2010)

Http://Www.Gouldspumps.Com/Download_Files/391

0/35482.Pdf.

Ilich, N. & Simonovic, S. P. (1998) Evolutionary

Algorithm For Minimuzation of Pumping Cost.

Journal of Computing In Civil Engineering, 12, 9.

Jowitt, P. W. & Germanopoulos, G. (1992) Optimal Pump

Scheduling In Water Supply Networks. Journal Of

Water Resources Planning And Management, 118, 17.

Kang, Y. H., Zhang, Z. & Huang, W. (2009)

Nsga-Ii Algorithms For Multi-Objective Short-Term

Hydrothermal Scheduling Power And Energy

Engineering Conference, Appeec. Asia-Pacific.

Lansey, K. E. & Awumah, K. (1994) Optimzal Pump

Operations Considering Pump Switches. Journal Of

Water Resources Planning And Management, 120, 19.

Lindell, E., Ormsbee, K. & Lansey, E. (1994) Optimal

Control of Water Supply Pumping Systems. Journal of

Water Resources Planning And Management, 120,

237-252.

Meetings Minutes (Spring And Fall 2009) Meetings

Between The University Of Calgary's Softqual

Research Team And Pembina Pipeline Staff.

Mennon, E. S.

(2005) Piping Calculation Manual, New

York, Mcgraw-Hill.

Mora, T. E. (2008) Optimization Of Pipeline Operations

Using Biologically-Inspired Computationsal Models.

Department of Electrical And Computer Engineering.

Univarsity of Calgary.

Ostfeld, A. & Tubaltzev, A. (2008) Ant Colony

Optimization For Least-Cost Design And Operation

Of Pumping Water Distribution Systems. Journal Of

Water Resources Planning And Management, 134,

107-118.

Prindle, W. (Last Viewed: April 2010) Customer

Incentives For Energy Efficiency Through Electric

And Natural Gas Rate Design. National Action Plan

For Energy Efficiency, 2009. Http://Www.Epa.Gov/

Rdee/Documents/Rate_Design.Pdf.

Solanas, J. L. & Montolio, J. M. (1987) The Optimum

Operation Of Water Systems International Conference

MULTI-OBJECTIVE OPTIMIZATION OF BOTH PUMPING ENERGY AND MAINTENANCE COSTS IN OIL

PIPELINE NETWORKS USING GENETIC ALGORITHMS

161

On Computer Applications For Water Supply And

Distribution. Leicester, England.

Ssi (Last Viewed: April 2010) Ssi Scheduling.

Http://Www.Ssischeduling.Com/.

Tullis, J. P. (1989) Hydraulics Of Pipelines: Pumps,

Valves, Cavitation, Transients, Wiley-Interscience.

Ulanicki, B., Kahler, J. & Coulbeck, B. (2008) Modeling

The Efficiency And Power Characteristics Of A Pump

Group. Journal of Water Resources Planning And

Management, 134, 88-93.

Ulanicki, B., Kahler, J. & See, H. (2007) Dynamic

Optimization Approach For Solving An Optimal

Scheduling Problem In Water Distribution Systems.

Journal of Water Resources Planning And

Management, 133, 10.

Veloso, B. C., Pires, L. F. G. & Azevedo, L. F. A. (2004)

Optimization Of Pump Energy Consumption In Oil

Poipelines. International Pipeline Conference.

Calgary, Canada, Asme.

Webb, K. (2007) Non-Chronological Pipeline Analysis

For Batched Operations. Psig Annual Meeting.

Calgary, Alberta.

Wegley, C., Eusuff, M. & Lansey, K. (2000) Determining

Pump Operations Using Particle Swarm Optimization.

Joint Conference On Water Resource Engineering And

Water Resources Planning And Management.

Minneapolis, Minnesota, Usa.

Wright, S., Somani, M. & Ditzel, C. (1998) Compressor

Station Optimization. Denver, Usa, Pipeline

Simulation Interest Group.

Zessler, U. & Shamir, U. (1989) Optimal Operation of

Water Distribution Syatems. Journal of Water

Resources Planning And Management, 115, 18.

Zhang, Z. (1999) Fluid Transients And Pipeline

Optimization Using Genetic Algorithms. Graduate

Department of Civil And Environment Engineering.

University Of Toronto, Master's Thesis.

LIST OF NOTATIONS

Binary variable that indicates the status of the

pump on segment j at time t

CL The constant term of the Darcy-Weisbach equation

for segment j

Con Contracted volume of fluid that should be

transported in the time frame to the delivery point

located on node i

()

Cost

Operation cost function associated with pump j

at time t

Average pressure head associated with node i at

time t

min

H Minimum acceptable head of node i

Max

Maximum acceptable head of node i

P Power consumed by pump j at time t

Head added to the network by pump j at time t

PL Pressure loss of segment j at time t

Q Average flow rate associated with pipeline

segment j at time t

Max

Q Maximum acceptable flow rate of segment j

Ini

Summation of the flow entering node i at time t

Outi

Summation of the flow exiting node i at time t

S Ratio of the speed of the pump on segment j at

time t to its nominal speed

min

S Minimum ratio of the speed of the pump on

segment j to its nominal speed

Max

S Maximum ratio of the speed of the pump on

segment j to its nominal speed

SH Static head associated with node i

V Valve pressure drop of segment j at time t

AP First coefficient of the head versus flow and speed

equation of the pump on segment j

Second coefficient of the head versus flow and