TOWARDS FUZZY GRANULARITY CONTROL IN

PARALLEL/DISTRIBUTED COMPUTING

T. Trigo de la Vega

, P. Lopez-García

1,2

and S. Muñoz-Hernandez

IMDEA Software, Madrid, Spain

Spanish Research Council (CSIC), Madrid, Spain

School of Computer Science, Technical University of Madrid (UPM), Madrid, Spain

Keywords:

Fuzzy logic application, Parallel computing, Automatic parallelization, Granularity control, Scheduling, Com-

plexity analysis.

Abstract:

Automatic parallelization has become a mainstream research topic for different reasons. For example, mul-

ticore architectures, which are now present even in laptops, have awakened an interest in software tools that

can exploit the computing power of parallel processors. Distributed and (multi)agent systems also beneﬁt

from techniques and tools for deciding in which locations should processes be run to make a better use of

the available resources. Any decision on whether to execute some processes in parallel or sequentially must

ensure correctness (i.e., the parallel execution obtains the same results as the sequential), but also has to take

into account a number of practical overheads, such as those associated with tasks creation, possible migration

of tasks to remote processors, the associated communication overheads, etc. Due to these overheads and if the

granularity of parallel tasks, i.e., the “work available” underneath them, is too small, it may happen that the

costs are larger than the beneﬁts in their parallel execution. Thus, the aim of granularity control is to change

parallel execution to sequential execution or vice-versa based on some conditions related to grain size and

overheads. In this work, we have applied fuzzy logic to automatic granularity control in parallel/distributed

computing and proposed fuzzy conditions for deciding whether to execute some given tasks in parallel or se-

quentially. We have compared our proposed fuzzy conditions with existing (conservative) sufﬁcient conditions

and our experiments showed that the proposed fuzzy conditions result in more efﬁcient executions on average

than the conservative conditions.

1 INTRODUCTION

Automatic parallelization is nowadays of great inter-

est since highly parallel processors, which were pre-

viously only considered in high performance comput-

ing, have steadily made their way into mainstream

computing. Currently, even standard desktop and

laptop machines include multicore chips with up to

twelve cores and the tendency is that these ﬁgures

will consistently grow in the foreseeable future. Thus,

there is an opportunity to build much faster and even-

tually much better software by producingparallel pro-

grams or parallelizing existing ones, and to exploit

these new multicore architectures. Performing this by

hand will inevitably lead to a decrease in productiv-

ity. An ideal alternative is automatic parallelization.

There are however some important theoretical and

practical issues to be addressed in automatic para-

llelization. Two of them are: (i) preserving correct-

ness (i.e., ensuring that the parallel execution obtains

the same results as the sequential one) and (ii) (the-

oretical) efﬁciency (i.e., ensuring that the amount of

work performed by executing some tasks in para-

llel is not greater than the one obtained by executing

the tasks sequentially, or at least, there is no slow-

down). Solutions to these problems have already

been proposed, such as (Chassin and Codognet, 1994;

Hermenegildo and Rossi, 1995). However, these so-

lutions assume an idealized execution environment in

which a number of practical overheads such as those

associated with task creation, possible migration of

tasks to remote processors, the associated commu-

nication overheads, etc, are ignored. Due to these

overheads and if the granularity of parallel tasks, i.e.,

the “work available” underneath them, is too small,

it may happen that the costs of parallel execution are

larger than its beneﬁts. In order to take these practi-

cal issues into account, some methods have been pro-

Trigo de la Vega T., Lopez-García P. and Muñoz-Hernandez S..

TOWARDS FUZZY GRANULARITY CONTROL IN PARALLEL/DISTRIBUTED COMPUTING.

DOI: 10.5220/0003066100430055

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICFC-2010), pages

43-55

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

posed whereby the granularity of parallel tasks and

their number are controlled. The aim of granularity

control is to change parallel execution to sequential

execution or vice-versa based on some conditions re-

lated to grain size and overheads. Granularity control

has been studied in the context of traditional (Krua-

trachue and Lewis, 1988; McGreary and Gill, 1989),

functional (Huelsbergen, 1993; Huelsbergen et al.,

1994) and logic programming (Kaplan, 1988; Debray

et al., 1990; Zhong et al., 1992; López-García et al.,

1996). Taking all these theoretical and practical is-

sues into account, an interesting goal in automatic pa-

rallelization is thus to ensure that the parallel executi-

on will not take more time than the sequential one. In

general, this condition cannot be determined before

executing the task involved, while granularity con-

trol should intuitively be carried out ahead of time.

Thus, we are forced to use approximations. One clear

alternative is to evaluate a (simple) sufﬁcient condi-

tion to ensure that the parallel execution will not take

more time than the sequential one. This was the ap-

proach developed in (López-García et al., 1996). It

has the advantage of ensuring that whenever a given

group of tasks are executed in parallel, there will be

no slowdown with respect to their sequential execu-

tion. However, the sufﬁcient conditions can be very

conservativein some situations and lead to some tasks

being executed sequentially even when their parallel

execution would take less time. Although not pro-

ducing slowdown, this causes a loss in parallelization

opportunities, and thus, no speedup is obtained. An

alternative is to give up strictly ensuring the no slow-

down condition in all parallel executions and to use

some conditions that have a good average case beha-

vior. It is in this point where fuzzy logic can be suc-

cessfully applied to evaluate “fuzzy” conditions that,

although can entail eventual slowdowns in some exe-

cutions, speedup the whole computation on average

(always preserving correctness).

It is remarkable the originality of this approach

that is betting for the expressiveness of fuzzy logic to

improve the decision making in the ﬁeld of program

optimization and, in particular, in automatic program

parallelization, including granularity control.

1.1 Fuzzy Logic Programming

Fuzzy logic has been a very fertile area during the

last years. Specially in the theoretical side, but also

from the practical point of view, with the development

of many fuzzy approaches. The ones developed in

logic programming are specially interesting by their

simplicity. The fuzzy logic programming systems

replace their inference mechanism, SLD-resolution,

with a fuzzy variant that is able to handle partial truth.

Most of these systems implement the fuzzy resolu-

tion introduced by Lee in (Lee, 1972): the Prolog-Elf

system (Ishizuka and Kanai, 1985), the FRIL Prolog

system (Baldwin et al., 1995) and the F-Prolog lan-

guage (Li and Liu, 1990).

One of the most promising fuzzy tools for Prolog

was the “Fuzzy Prolog” system (Guadarrama et al.,

2004). Fuzzy Prolog adds fuzziness to a Prolog com-

piler using CLP(R ) instead of implementing a new

fuzzy resolution method, as other former fuzzy Pro-

logs do. It represents intervals as constraints over

real numbers and aggregation operators as operations

with these constraints, so it uses the Prolog built-in

inference mechanism to handle the concept of partial

truth.

1.1.1 RFuzzy

Besides the advantages of Fuzzy Prolog (Vaucheret

et al., 2002; Guadarrama et al., 2004), its truth value

representation based on constraints is too general,

which makes it complex to be interpreted by regular

users. That was the reason for implementing a sim-

pler variant that was called RFuzzy (Pablos-Ceruelo

et al., 2009a; Muñoz-Hernández et al., 2009; Pablos-

Ceruelo et al., 2009b; Strass et al., 2009). In RFuzzy,

the truth value is represented by a simple real number.

RFuzzy is implemented as a Ciao Pro-

log (Hermenegildo et al., 2008) package because

Ciao Prolog offers the possibility of dealing with a

higher order compilation through the implementation

of Ciao packages.

The compilation process of a RFuzzy program has

two pre-compilation steps: (1) the RFuzzy program is

translated into CLP(R ) constraints by means of the

RFuzzy package and (2) the program with constraints

is translated into ISO Prolog by using the CLP(R )

package.

As the motivation of RFuzzy was providing a tool

for practical application, it was loaded with many nice

features that represent an advantage with respect to

previous fuzzy tools to model real problems. That is

why we have chosen RFuzzy for the implementation

of our prototype in this work.

2 THE GRANULARITY

CONTROL PROBLEM

We start by discussing the basic issues to be addressed

in our approach to granularity control, in terms of the

generic execution model described in (López-García

et al., 1996). In particular, we discuss how conditions

ICFC 2010 - International Conference on Fuzzy Computation

for deciding between parallel and sequential execu-

tion can be devised. We consider a generic executi-

on model: let g = g

,...,g

be a task such that sub-

tasks g

,...,g

are candidates for parallel execution.

represents the cost (execution time) of the sequen-

tial execution of g and T

represents the (sequential)

cost of the execution of subtask g

There can be many different ways to execute g

in parallel, involving different choices of scheduling,

load balancing, etc., each having its own cost (exe-

cution time). To simplify the discussion, we will as-

sume that T

represents in some way all of the possi-

ble costs. More concretely, T

≤ T

should be under-

stood as “T

is greater or equal than any possible value

for T

.”

In a ﬁrst approximation, we assume that the points

of parallelization of g are ﬁxed. We also assume, for

simplicity, and without loss of generality, that no tests

– such as, perhaps, “independence” tests (Chassin and

Codognet, 1994; Hermenegildo and Rossi, 1995) –

other than those related to granularity control are nec-

essary. Thus, the purpose of granularity control will

be to determine, based on some conditions, whether

the g

’s are going to be executed in parallel or se-

quentially. In doing this, the objective is to improve

the ratio between the parallel and sequential executi-

on times.

Performing an accurate granularity control at

compile-time is difﬁcult since most of the informa-

tion needed, as for example, input data size, is only

known at run-time. An useful strategy can be to do as

much work as possible at compile-time and postpone

some ﬁnal decisions to run-time. This can be achieved

by generating at compile-time cost functions which

estimate task costs as a function of input data sizes,

which are then evaluated at run-time when such sizes

are known. Then, after comparing costs of parallel

and sequential executions, it can be determined which

of these types of executions must be performed. This

scheme was proposed by (Debray et al., 1990) in the

context of logic programs and by (Rabhi and Manson,

1990) in the context of functional programs. An inter-

esting goal is to ensure that T

≤ T

. In general, this

condition cannot be determined before executing g,

while granularity control should intuitively be carried

out ahead of time. Thus, we are forced to use approx-

imations. The way in which these approximations can

be performed, is the subject of the two following sec-

tions.

3 THE CONSERVATIVE (SAFE)

APPROACH

The approach proposed in (López-García et al., 1996)

consists on using safe approximations, i.e., evaluating

a (simple) sufﬁcient condition to ensure that the para-

llel execution will not take more time than the sequen-

tial one. Ensuring T

≤ T

corresponds to the case

where the action taken when the condition holds is to

run in parallel, i.e., to a philosophy were tasks are ex-

ecuted sequentially unless parallel execution can be

shown to be faster. We call this “parallelizing a se-

quential program.” The converse approach, “sequen-

tializing a parallel program,” corresponds to the case

where the objective is to detect whether the sufﬁcient

condition T

≤ T

holds.

Parallelizing a Sequential Program. In order to

derivea sufﬁcient condition for the inequality T

≤ T

we obtain upper bounds for its left-hand-side and

lower bounds for its right-hand-side, i.e., a sufﬁcient

condition for T

≤ T

is T

≤ T

, where T

denotes an

upper bound on T

and T

a lower bound on T

. We

will use the superscripts l and u to denote lower and

upper bounds respectively throughout the paper. The

discussion about how these upper and lower bounds

on the sequential and parallel execution times can be

estimated are outside the scope of this paper. We refer

the reader to (Mera et al., 2008) and (López-García

et al., 1996) for a full description of compile-time

analysis that obtain lower and upper bounds on se-

quential and parallel execution times respectively as

functions of input data sizes.

Sequentializing a Parallel Program. Assume now

that we want to detect when T

≤ T

holds, because

we have a parallel program and want to proﬁt from

performing some sequentializations. In this case, a

sufﬁcient condition for T

≤ T

is T

≤ T

4 THE FUZZY APPROACH

In some scenarios, it is not allowed to perform para-

llelizations if it does not ensure any speedup. How-

ever, in most environments it is justiﬁed to sacri-

ﬁce efﬁciency in some cases in order to improve the

speedup on average or in the majority of the cases.

Thus our approach is to give up strictly ensuring that

≤ T

holds and to use some relaxed heuristics using

fuzzy logic able to detect favorable cases.

We use as a decision criteria the formula T

≤ T

It is easy to transform the formula in 1 ≤ T

or the

TOWARDS FUZZY GRANULARITY CONTROL IN PARALLEL/DISTRIBUTED COMPUTING

equivalent T

≥ 1. We are implicitly using a crisp

criteria in the sense that we use an operator whose

truth values are deﬁned mathematically.

If we move to classical logic and want to rep-

resent the condition of parallelizing or not a set of

subtasks using a logic predicate, we could deﬁne

greater/2 as a predicate of two arguments that is suc-

cessful if the ﬁrst one is greater than the second one

and false otherwise. We could check the condition

greater(T

,1) or rename this condition to a logic

predicate, greater1/1, of arity 1 that compares its ar-

gument with 1, succeeds if it is greater than 1 and

fails otherwise (i.e., greater1(1.8) succeeds, whereas

greater1(0.8) fails). With the boolean condition rep-

resented by the predicate greater1/1 it is easy to fol-

low the conservative approach presented in Section 3.

For a gentle intuition to fuzzy logic, we continue

talking about this predicate. We can see that the con-

cept of being “greater than” is very strict in the sense

that some cases in which the value is close to 1 are

going to be rejected. Let us introduce the concept of

truth value. Till now we have been using two truth

values true and false, or 1 and 0. But if we intro-

duce levels of truth we could for example provide for

a logic predicate intermediate truth values in between

0 and 1. We have deﬁned other predicates similar to

greater1/1 that are more ﬂexible in their semantics.

They are quite_greater/1 and rather_greater/1. Their

deﬁnition is clearer in Figure 1 (and described in Sec-

tion 5.1). With this set of predicates we are going to

deﬁne a fuzzy framework for the experimental possi-

bilities of using a fuzzy criteria to take decisions about

parallelization of tasks.

4.1 Decision Making

Instead of deciding about the goodness of the para-

llelization depending on a crisp condition as in the

conservative approach, in this paper we are going to

make the decision attending to a couple of certainty

factors: SEQ, the certainty factor that is going to rep-

resent the preference (its truth value) for executing

the sequential variant of a program, and PAR, the cer-

tainty factor that is going to represent the preference

(its truth value) for executing the parallel variant of

such program. Both certainty factors are real num-

bers, SEQ, PAR ∈ [0,1]. The way of assigning a value

to each certainty factor is not unique. We can de-

ﬁne different fuzzy heuristics for their calculation. In

Section 5.2 we are going to compare a set of them to

choose (in Section 5.3) our selected model.

Once the values of SEQ and PAR have been al-

ready assigned, if PAR > SEQ then our task schedul-

ing prototype executes the parallel variant of the pro-

gram, otherwise it executes the sequential one.

5 EXPERIMENTAL RESULTS

We have developed a prototype (Section 5.1) of a

fuzzy task scheduler based on the approach described

in Section 4. We have prepared a common frame-

work to test the behavior of a set of different heuristics

(Section 5.2) and we have compared them also with

the rules of the conservative approach (Section 3) in

order to be able to select the best results (Section 5.3).

For a better understanding of these experiments, we

present the behavior of our prototype for a progres-

sion of execution time data (Section 5.4). Finally, we

have tested our prototype with real programs (Sec-

tion 5.5) in order to demonstrate that it can be suc-

cessfully applied in practice.

5.1 Prototype Implementation

All the granularity control methods have been imple-

mented in Ciao Prolog. The classical logic rules have

been implemented using the CLP(Q) package and the

fuzzy logic rules using the Rfuzzy package.

We havedecided to use logic programmingfor im-

plementing our approach because of its simplicity and

for taking the advantage of some useful extensions

provided by the Ciao Prolog framework. In partic-

ular, Ciao Prolog has integrated static analysis tech-

niques for obtaining upper and lower bounds on exe-

cution times and a fuzzy library for the calculation of

certainty factors.

As explained before, in our new approach to gran-

ularity control, the decision of how to execute is based

on the certainty factors associated to both, sequential

and parallel executions. So that, ﬁrst of all, we have

to quantify such certainty and then decide how to exe-

cute. The value to the certainty factors is provided by

fuzzy rules that are able to combine fuzzy values us-

ing aggregation operators. According to RFuzzy syn-

tax:

SEQ(P,V

) : op cond

),cond

),·· · , cond

PAR(P,V

) : op

′

cond

′

),cond

′

),·· · ,cond

′

The truth value V

represents how much executing the

program P in a sequential way is adequate. V

is ob-

tained by combining the truth values of the partial

conditionsV

,...,V

with the aggregation operator op.

Symmetrically, V

represents how much adequate is

the parallel execution for the program P.

The bigger factor (SEQ or PAR) will point out the

selected execution (sequential or parallel).

In order to test the behavior of our method we

have developed a set of conditions comparing a group

ICFC 2010 - International Conference on Fuzzy Computation

0.2

0.4

0.6

0.8

-20 -15 -10 -5 0 5 10 15 20

Ratio

0.2

0.4

0.6

0.8

-20 -15 -10 -5 0 5 10 15 20

Ratio

0.2

0.4

0.6

0.8

-20 -15 -10 -5 0 5 10 15 20

Ratio

Greater. Quite greater. Rather greater.

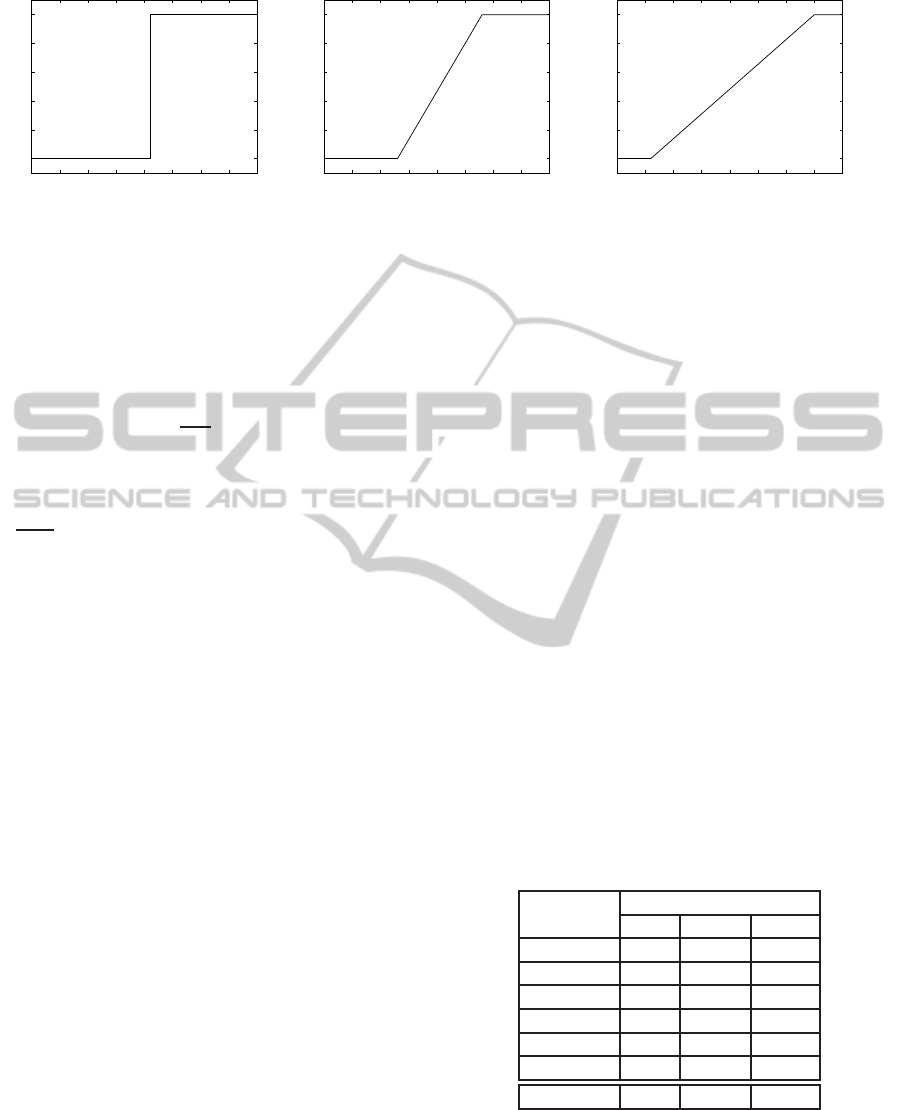
Figure 1: Fuzzy sets for greater.

of values of execution times: {T

}

by pairs. The comparison that makes each condition

is calculated with the fuzzy relations quite_greater

and rather_greater (represented in Figure 1), whose

deﬁnitions are:

quite_greater(X) =







0 if X ≤ −7

X+7

if −7 < X < 8

1 if X ≥ 8

rather_greater(X) =







0 if X ≤ −14

X+14

if −14 < X < 15

1 if X ≥ 15

We also use the relative harmonic difference, an

experimental relation described in (Mera et al., 2008)

as follows:

harmonic_dif f(X,Y) = (X −Y) ∗ (1/X + 1/Y)/2.

We have selected this relation because it compares

two numbers in a relative and symmetric way, i.e.:

harmonic_dif f(X,Y) = −harmonic_dif f(Y, X).

The harmonic difference only works well for positive

numbers, but as we are working with execution times,

it is enough for our purposes.

These fuzzy relations can be redeﬁned with differ-

ent bounds, although in this prototype we have only

used the values 0, 7 and 14. These bounds have been

selected according to the magnitude of the execution

times that we provide for the programs (see Table 2)

in order to obtain signiﬁcant results depending on the

selected fuzzy relation.

5.2 Heuristic Comparison

In this section we discuss the evaluation of our pro-

totype with different aggregation operators. A suite

of benchmarks to test the prototype has been devel-

oped. Each benchmark has been deﬁned in terms of

its execution times (average, upper and lower bounds

on parallel and sequential execution times) in order

to see if the new approach provides better results

than the conservative one. Obviously, in real cases,

these values will need to be estimated at compile-

time using a program analyzer like, for example,

CiaoPP (Hermenegildo et al., 2005; Mera et al.,

2008). Table 2 contains the description of the bench-

marks. Each row shows the information of one pro-

gram. The ﬁrst column contains the name of the pro-

gram and, under it and between brackets, the name of

the ﬁgure which contains the graphical representation

of the benchmark. This ﬁgure allows to identify the

optimal execution in a graphic way. The following

columns show : T

(lower bound on sequential execu-

tion time), T

(averagesequential execution time), T

(upper bound on sequential executiontime), T

(lower

bound on parallel execution time), T

(average para-

llel execution time) and T

(upper bound on parallel

execution time). Each execution time is in microsec-

onds.

Figures 2, 3, 4, 5, 6 and 7 describe the benchmarks

in a graphic way. In horizontal we ﬁnd both (parallel

and sequential) executions. In vertical we ﬁnd, for

each execution, the interval comprised between its up-

per and lower bound on execution time.

To make things simpler, we refer to the fuzzy set

as gt, and to the relative harmonic difference relation

as hd.

The rules of fuzzy logic for calculating each condition

Table 1: Aggregation operators execution time.

Program

Aggregation Operator

max dprod dluka

p1 1.23 1.11 1.04

p2 0.42 0.51 0.45

p3 0.93 0.88 0.88

p4 0.43 0.51 0.45

p5 0.62 0.76 0.63

p6 0.56 0.62 0.57

average 0.70 0.73 0.67

PAR

or SEQ

, 1 ≤ i ≤ 7 (see Table 3), have been com-

posed using several aggregation operators but the re-

sults have shown that only the t-conorms max (max),

Lukasiewicz (dluka) and sum (dprod) are correct (i.e.,

always suggest the optimal execution) so we do not

TOWARDS FUZZY GRANULARITY CONTROL IN PARALLEL/DISTRIBUTED COMPUTING

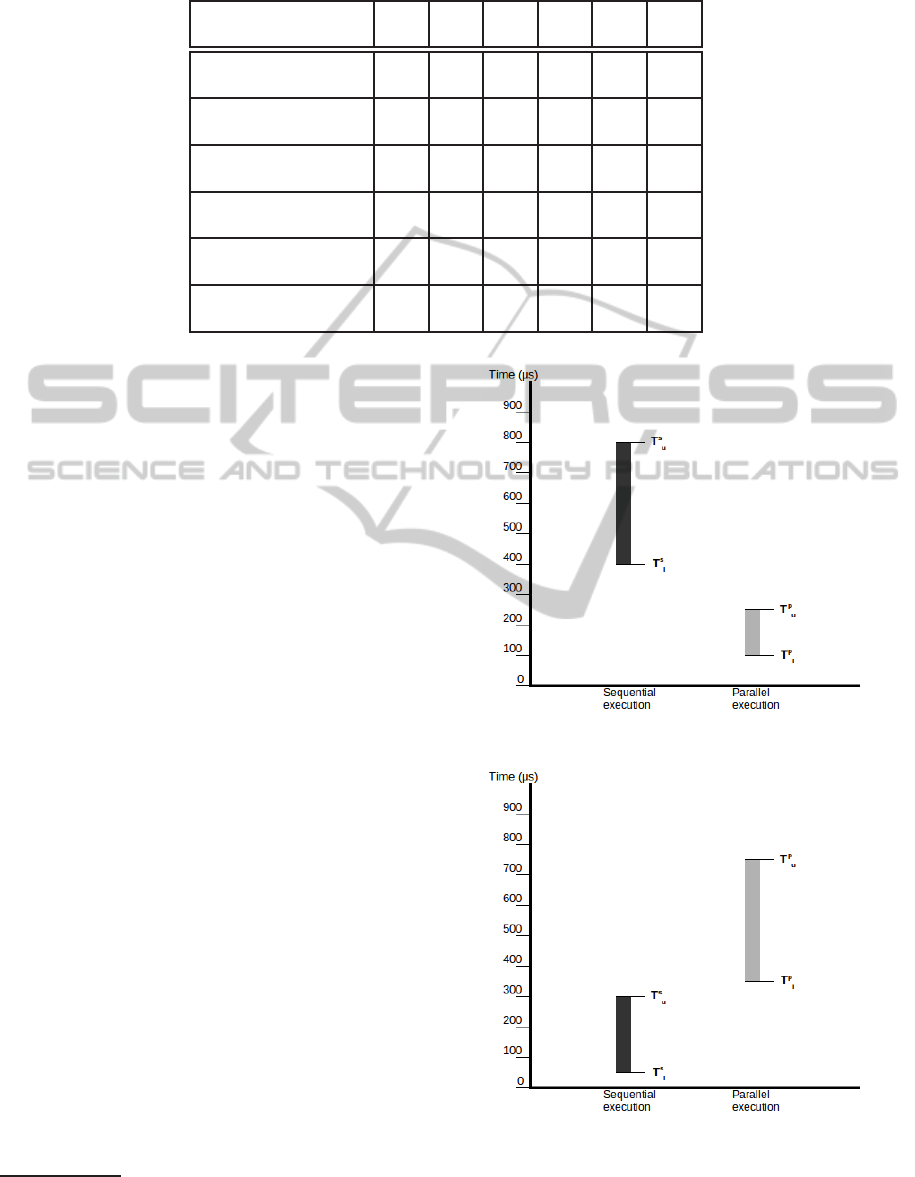
Table 2: Benchmark program execution times (in microseconds).

Program

Time

p1 400 600 800 100 175 250

(Figure 2)

p2 50 175 300 350 550 750

(Figure 3)

p3 250 525 800 300 375 450

(Figure 4)

p4 50 150 250 100 325 550

(Figure 5)

p5 200 400 600 200 325 450

(Figure 6)

p6 150 325 500 100 275 450

(Figure 7)

show the rest of the tested operations

in the results.

We have seen how the three t-conorms max (max),

Lukasiewicz (dluka) and sum (dprod) have the same

behavior. Thus, in order to chose one of these aggre-

gation operators, we have followed the criteria of the

one more efﬁciently evaluated. In this sense, we have

measured the execution time of evaluating the condi-

tion PAR

for each program using the three operators.

These execution times have been obtained over an In-

tel platform (Intel Pentium 4 CPU 2.60GHz). They

are shown in Table 1. The ﬁrst column shows the

name of the program (see Table 2) and the three next

ones, the aggregation operators. Each row shows the

execution time (in microseconds) of the evaluation of

the condition PAR

(see Table 3) for the program us-

ing the three mentioned operators. The last row con-

tains, for each operator, an average value on the exe-

cution time of evaluating such condition for all the

programs. As we can see, the results are very simi-

lar for the aggregation operators max and dluka while

for dprod are almost always bigger. Although max is

a little bit less efﬁcient (on average) than dluka, max

seems to be the best option due to its simplicity.

The whole set of proposed certainty factors and

the results for each approach are shown in Table 3.

They correspond to the case of parallelizing a sequen-

tial program (i.e., where the action taken by default

when there is no evidence towards executing is pa-

rallel is to execute sequentially). The ﬁrst column

shows the name of the program. The second col-

umn shows what would be the right (optimal) deci-

sion about the type of execution that should be per-

formed (either parallel or sequential). The rest of the

columns contain the results of evaluating the condi-

tions. Columns 3 and 4 contain the results obtained

The rest of the tested operations are: min, luka and

prod.

Figure 2: Program p1.

Figure 3: Program p2.

ICFC 2010 - International Conference on Fuzzy Computation

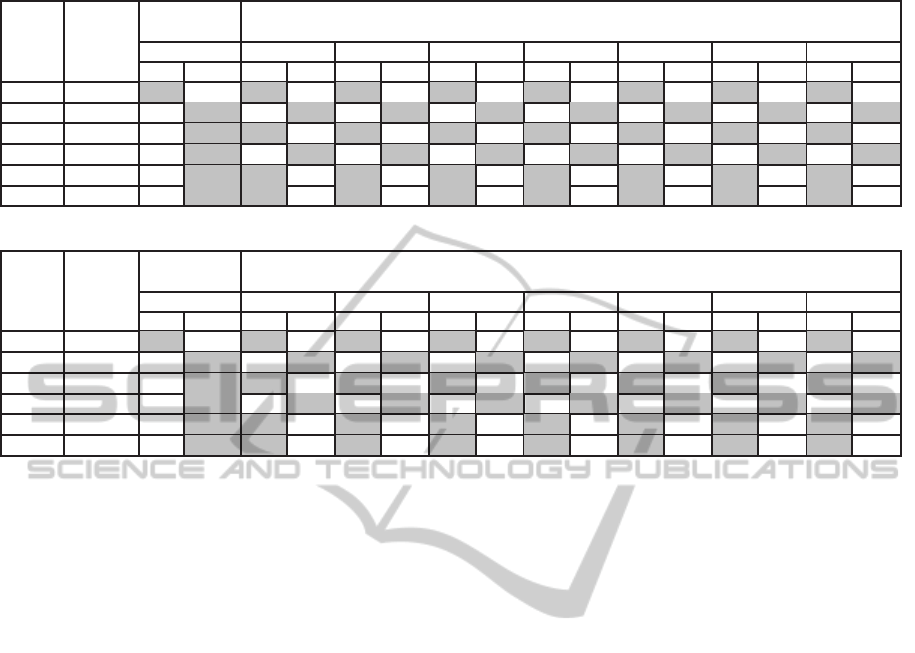
Table 3: Selected executions using the whole set of rules.

Program Optimal

Classical Logic Fuzzy Logic

(Greater) (Quite greater)

Classical Fuzzy 1 Fuzzy 2 Fuzzy 3 Fuzzy 4 Fuzzy 5 Fuzzy 6 Fuzzy 7

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

p1 Parallel 1 0 0.73 0.48 0.73 0.48 0.73 0.48 0.57 0.35 0.57 0.35 0.57 0.35 0.57 0.36

p2 Sequential 0 1 0.48 0.93 0.49 0.93 0.49 0.93 0.34 0.58 0.33 0.59 0.34 0.58 0.31 0.58

p3 Parallel 0 0 0.56 0.54 0.58 0.54 0.58 0.54 0.48 0.44 0.48 0.44 0.48 0.44 0.47 0.44

p4 Sequential 0 0 0.5 0.61 0.5 0.61 0.5 0.61 0.41 0.52 0.41 0.52 0.41 0.52 0.41 0.52

p5 Parallel 0 0 0.54 0.53 0.55 0.53 0.55 0.53 0.47 0.45 0.47 0.45 0.47 0.45 0.47 0.45

p6 Parallel 0 0 0.56 0.52 0.56 0.52 0.56 0.52 0.48 0.45 0.48 0.45 0.48 0.45 0.48 0.45

Program Optimal

Classical Logic Fuzzy Logic

(Greater) (Rather greater)

Classical Fuzzy 1 Fuzzy 2 Fuzzy 3 Fuzzy 4 Fuzzy 5 Fuzzy 6 Fuzzy 7

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

PAR

SEQ

p1 Parallel 1 0 0.62 0.49 0.62 0.49 0.62 0.49 0.53 0.42 0.53 0.42 0.53 0.42 0.54 0.42

p2 Sequential 0 1 0.49 0.72 0.49 0.72 0.49 0.72 0.41 0.54 0.41 0.55 0.41 0.54 0.4 0.54

p3 Parallel 0 0 0.53 0.52 0.54 0.52 0.54 0.52 0.49 0.47 0.49 0.47 0.49 0.47 0.48 0.47

p4 Sequential 0 0 0.5 0.55 0.5 0.55 0.5 0.55 0.45 0.51 0.45 0.51 0.45 0.51 0.45 0.51

p5 Parallel 0 0 0.52 0.51 0.52 0.51 0.52 0.51 0.48 0.47 0.48 0.47 0.48 0.47 0.48 0.47

p6 Parallel 0 0 0.53 0.51 0.53 0.51 0.53 0.51 0.49 0.47 0.49 0.47 0.49 0.47 0.49 0.47

Conditions:

PAR

is T

≤ T

SEQ

is T

≤ T

PAR

is max(gt(T

),gt(T

))

SEQ

is max(gt(T

),gt(T

))

PAR

is max(gt(T

),gt(T

))

SEQ

is max(gt(T

),gt(T

))

PAR

is max(gt(T

),gt(T

))

SEQ

is max(gt(T

),gt(T

))

PAR

is rel_hd(0.5∗ hd(T

) + 0.25∗ hd(T

))

SEQ

is rel_hd(0.5∗ hd(T

) + 0.25∗ hd(T

))

PAR

is rel_hd((hd(T

) + hd(T

))/3)

SEQ

is rel_hd((hd(T

) + hd(T

))/3)

PAR

is rel_hd(0.25∗ hd(T

) + 0.5∗ hd(T

) + 0.25∗ hd(T

))

SEQ

is rel_hd(0.25∗ hd(T

) + 0.5∗ hd(T

) + 0.25∗ hd(T

))

PAR

is rel_hd(0.25∗ hd(T

) + 0.25∗ hd(T

) + 0.5∗ hd(T

))

SEQ

is rel_hd(0.25∗ hd(T

) + 0.25∗ hd(T

) + 0.5∗ hd(T

))

using the conservative approach, while columns 5-

18 contain the results obtained using our proposed

conditions based on fuzzy logic. Each column in

the later group of columns corresponds to a differ-

ent fuzzy condition. The selected type of execution

(using the process explained in Section 4.1) are high-

lighted. SEQ

and PAR

are the truth values obtained

for the certainty factors of the sequential and para-

llel executions of the program p

. We have performed

the experiments for two different levels of ﬂexibility

using quite_greater and rather_greater respectively.

The decisions made by using the fuzzy conditions are

always the optimal ones for these experiments. How-

ever, the conservative approach (classical logic) dis-

agrees with the optimal ones in half of the cases. For

example, the condition T

≤ T

holds for p1 (see Fig-

ure 2). Thus, the parallel execution of p1 is more

efﬁcient than the sequential one. In this case, both

the conservative approach (classical logic) and the

fuzzy logic approach agree in that the execution of p1

should be parallel. The converse condition (T

≤ T

)

holds for program p2 (see Figure 3), and thus, the op-

timal action is executing it sequentially. In this case,

also both approaches agree in that the execution of p2

should be parallel.

For programs 3-6, the classical logic truth values

(PAR

and SEQ

) are always zero, which means that

the suggested type of execution is sequential for all

of these programs (i.e., the default type of executi-

on). However, from Figures 4, 5, 6 and 7, we can see

that in some cases the optimal decision is to execute

these programs in parallel. For example, consider

program p3 (see ﬁgure 4). We have that T

= 450 µs

TOWARDS FUZZY GRANULARITY CONTROL IN PARALLEL/DISTRIBUTED COMPUTING

Table 4: Progression of decisions using the fuzzy set quite greater.

Execution Optimal

Classical Logic Fuzzy Logic

(Greater) (Quite greater)

Classical Fuzzy 2

PAR

SEQ

PAR

SEQ

p3_execution1 Parallel 1 0 0.68 0.49

p3_execution2 Parallel 0 0 0.64 0.5

p3_execution3 Parallel 0 0 0.61 0.52

p3_execution4 Parallel 0 0 0.6 0.53

p3_execution5 Parallel 0 0 0.58 0.54

p3_execution6 Parallel 0 0 0.57 0.56

p3_execution7 Sequential 0 0 0.56 0.57

p3_execution8 Sequential 0 0 0.55 0.58

p3_execution9 Sequential 0 0 0.54 0.6

p3_execution10 Sequential 0 0 0.54 0.61

p3_execution11 Sequential 0 0 0.53 0.62

p3_execution12 Sequential 0 0 0.53 0.64

p3_execution13 Sequential 0 0 0.52 0.65

p3_execution14 Sequential 0 0 0.52 0.66

p3_execution15 Sequential 0 1 0.52 0.68

Conditions:

PAR

is T

≤ T

SEQ

is T

≤ T

PAR

is max(gt(T

),gt(T

))

SEQ

is max(gt(T

),gt(T

))

Figure 4: Program p3.

and T

= 250 µs, and thus T

≤ T

does not hold.

The decision of executing p3 sequentially made by

classical logic is safe. However, in this case, since

= 800 µs, assuming that p3 is run a signiﬁcant

number of times, we have that on average, executing

p3 in parallel would be more efﬁcient than executing

it sequentially. In contrast, our proposed fuzzy ap-

proach selects the optimal type of execution for p3: its

two subtasks should be executed in parallel. Program

Figure 5: Program p4.

p4 (see ﬁgure 5) represents the opposite case. In this

case T

= 250 µs and T

= 100 µs so T

≤ T

does not

hold. But in this case T

= 550 µs and T

= 250 µs.

Thus, the best choice seems to be executing p4 se-

quentially. This is the type of execution suggested

by our fuzzy conditions. However, using classical

logic, the selected execution is sequential (the one se-

lected by default when none of the sufﬁcient condi-

tions PAR

nor SEQ

hold). However, our fuzzy logic

ICFC 2010 - International Conference on Fuzzy Computation

Figure 6: Program p5.

Figure 7: Program p6.

conditions provide enough evidences that support the

decision of executing in parallel.

In the situations illustrated by the last two pro-

grams it is not so clear what type of execution should

be selected. For program p5 we have that T

= 450 µs

and T

= 200 µs. Thus, since the sufﬁcient condi-

tion T

≤ T

for executing in parallel does not hold,

it seems that the program should be executed sequen-

tially. However, since T

= 200 µs and T

= 600 µs,

the sufﬁcient condition T

≤ T

for executing in pa-

rallel does not hold either. Now, using our fuzzy logic

approach, taking the four values T

and T

into account, a certainty factor of nearly 0.5 suggests

that the best choice is to execute p5 in parallel.

For program p6 (see ﬁgure 7), none of the sufﬁ-

cient conditions T

≤ T

and T

≤ T

(for selecting

parallel and sequential execution respectively) hold.

However, since T

≤ T

and T

≤ T

hold, it is clear

that the execution time of the sequential execution is

going to belong to an interval whose limits are big-

ger than the limits of the parallel execution. Thus,

is it more likely that the execution time of the para-

llel execution be less than the execution time of the

sequential one, so that the right decision seems to ex-

ecute p6 in parallel. We can see that our proposed

fuzzy conditions also suggests the parallel execution.

Finally, we can see that in those cases in which

classical logic suggests a type of execution (with truth

value 1), our fuzzy logic approach suggests the same

type of execution (sequential or parallel).

5.3 Selected Fuzzy Model

Table 3 shows that all the fuzzy conditions (Fuzzy 1-

7) select the same type of execution, sequential or

parallel (independently of the fuzzy set used, either

quite_greater or rather_greater). Our goal is to de-

tect those situations where the parallel execution is

faster than the sequential one, such that a conserva-

tive (safe) approach is not able to detect it but the

fuzzy approach is. Approaches Fuzzy 4, 5, 6 and

7 suggest parallel execution with less evidence than

Fuzzy 1, 2 and 3 for both fuzzy sets (quite_greater

and rather_greater). As we are interested in suggest-

ing to execute in parallel with evidences as bigger as

possible we rule out this subset of conditions and we

focus our attention in the ﬁrst set. Both Fuzzy 2 and 3

obtain the same values in all cases. Furthermore they

provide higher evidences for parallel execution than

the condition Fuzzy 1. This fact can be seen in pro-

grams p3, p5 and p6. As Fuzzy 2 is a subset of Fuzzy

3, evaluating the ﬁrst one is more efﬁcient than the

second one (the Fuzzy 3 condition has one more com-

parison). Thus, the condition that we have selected is

Fuzzy 2:

PAR is max(gt(T

),gt(T

))

This condition obtains a better average case behav-

ior by relaxing decision conditions (and losing some

precision). There may be cases in which our ap-

proach will select the slowest execution, however it

will select the fastest one in a bigger number of cases.

This tradeoff between safety and efﬁciency makes this

new approach only applicable to non-critical systems,

where no constraints about execution times must be

met, and a wrong decision will only cause a slow-

down which is admissible. In the same way that it

happens in the conservative approach, the fuzzy ap-

proach for sequentializing a parallel program is also

symmetric to the problem of parallelizing a sequen-

tial program. The condition that we have selected for

sequentializing a parallel program is:

SEQ is max(gt(T

),gt(T

))

TOWARDS FUZZY GRANULARITY CONTROL IN PARALLEL/DISTRIBUTED COMPUTING

5.4 Decisions Progression

Focusing on program p3 and using the fuzzy set

quite_greater with the selected fuzzy model (in Sec-

tion 5.3) we have developed an incremental experi-

ment whose results are shown in Table 4. The main

goal is to see how with this fuzzy logic approach

we can select the optimal execution in those cases in

which the conservative approach is not able to give a

conclusion, and also, how our fuzzy logic approach

detects all situations (safely) detected optimal by the

conservative approach. Figure 8 shows all the exe-

cution scenarios. The sequential execution times are

ﬁxed, while the parallel execution ones depend on

each scenario. The later are represented by pairs

(i),T

(i)) where i is the concrete case. The pa-

rallel execution times of each scenario are the times

of the previous one plus 50 units, in order to appre-

ciate the progression. The times of the ﬁrst scenario

are T

(1) = 100 µs and T

(1) = 250 µs. Attending to

classical logic we can see how only when PAR

= 1

or SEQ

= 1 we obtain a justiﬁed answer (that the

program must be executed in parallel or sequentially

respectively). In the rest of the cases the selected type

of execution is sequential by default, since we are

following the philosophy of parallelizing a sequential

program, and there are no evidences towards either

type of execution. On the other hand, fuzzy logic al-

ways selects the optimal execution (supported by evi-

dences).

5.5 Experiments with Real Programs

The former experiments (Section 5.2) have shown that

our fuzzy granularity control framework is able to

capture which is the optimal type of execution on av-

erage. Moreover, in order to ensure that our approach

can be applied in practice, we have performed some

experiments with real programs (and real execution

times). The experimental assessment have been made

over an UltraSparc-T1, 8 cores x 1GHz (4 threads per

core), 8GB of RAM, SunOS 5.10.

We have tested the fuzzy model selected in Sec-

tion 5.3, so that only upper and lower bounds on (pa-

rallel and sequential) execution times were needed.

Sequential execution times have been measured di-

rectly over the execution platform (executing the

worst and best possible cases) while the parallel ones

have been estimated.

The number of cores of the processor is denoted

as p, the number of tasks (candidates for parallel or

sequential execution) as n, and the relation ⌈n/p⌉ is

denoted as k. We consider two different overheads

of parallel execution: (a) the time needed for creat-

Table 5: Real programs for experimental assessment.

Qsort qsort(n) sorts a list of n random elements.

Fib ﬁb(n) obtains the nth Fibonacci number.

Hanoi hanoi(n) solves Hanoi puzzle with 3 rods

and n disks.

ing n parallel tasks, called Create(n), and (b) an upper

bound on the time taken from the point in which a pa-

rallel subtask g

is created until its execution is started

by a processor, denoted as SysOverhead

. Both types

of overheads have been experimentally measured for

the execution platform. For the ﬁrst one, we have

measured directly the time of creating p threads. The

second one has been obtained by using the expression

(S/2) − P, where S and P are the measured execu-

tion times of a program consisting of two perfectly

balanced tasks running with one and two threads re-

spectively.

There are different ways of executing a task in pa-

rallel depending on the scheduling. The highest pa-

rallel execution time will be the one with the worst

scheduling (i.e., the one in which the cores are idle as

much as possible). Consider a task g = g

,...,g

such

that subtasks g

,...,g

are candidates for parallel exe-

cution. Assume that Ts

represents the cost (execution

time) of the execution of subtask g

. Assume also that

,Ts

,...,Ts

are in descending order of cost and

that an ideal parallel execution environment has no

parallel execution overheads. Then, we can estimate

and T

as follows:

= T

/p (1)

= Create(p) +

∑

i=1

(SySoverhead

+ T

) (2)

Table 6 shows the experimental results. The ﬁrst

four columns show the same information as in Ta-

ble 3, although in this table Program refers to the

benchmarks in Table 5. For space reasons, Table 6

only shows results for a subset of inputs. In particu-

lar, Fibonacci and Hanoi have been tested with the set

of inputs {1,18} and {1,14} respectively. The assess-

ment of the fuzzy approach proposed in this paper is

similar for the whole set of tested inputs. The last row

shows the speedup of our fuzzy approach with respect

to the conservative approach: speedup =

, where

is the time of the selected execution using the con-

servative approach and T

is the time of the selected

execution using our fuzzy approach. A positive value

of speedup means that the execution selected with our

approach is faster than the one selected by the conser-

vative approach.

ICFC 2010 - International Conference on Fuzzy Computation

Figure 8: Progression of executions of the example program p3.

Our fuzzy conditions obtain, in the worst case, the

same results (Speedup = 1.0) than the conservative

one. In the rest of the cases, it improves the perfor-

mance of the conservative approach.

We can distinguish two main sets of cases in Ta-

ble 6: one set made up of qsort and the other set made

up of ﬁb and hanoi. In the ﬁrst set the upper bound

on the sequential execution time is different from the

lower bound, while in the second set both bounds are

the same. Our approach improves the conservative

one in the ﬁrst set of cases, whereas in the second set,

it provides the same performance than the conserva-

tive approach. This is understandable, since the exe-

cution time for the ﬁrst set of cases not only depends

on the length of the input list, but also on the values of

its elements. Thus, for a given list length, there may

be different execution times, depending on the actual

values of the lists with such length. However, in the

second set of cases, the execution time only depends

on the size (using the integer value metric) of the in-

put argument, and all executions for the same input

data size take the same execution time.

6 CONCLUSIONS

We have applied fuzzy logic to the program optimiza-

tion ﬁeld, in particular, to automatic granularity con-

trol in parallel/distributed computing. We have de-

rived fuzzy conditions for deciding whether to exe-

cute some tasks in parallel or sequentially, using in-

formation about the cost of tasks and parallel executi-

on overheads.

We have performed an experimental assessment of

the fuzzy conditions and identiﬁed the ones that have

the best average case behavior. We have also com-

pared our proposed fuzzy conditions with existing

sufﬁcient (conservative) ones for performing granu-

larity control. Our experiments showed that the pro-

posed fuzzy conditions result in better program opti-

mizations (on average) than the conservative condi-

tions. The conservative approach ensures that exe-

cution decisions will never result in a slowdown, but

loses some parallelizations opportunities (and thus,

no speedup is obtained). In contrast, the fuzzy ap-

proach makes a better use of the parallel resources

and although fuzzy conditions can produce slowdown

for some executions, the whole computation beneﬁts

from some speedup on average (always preserving

correctness). Of course, the fuzzy approach is appli-

cable in scenarios where the no slowdown property is

not needed, as for example video games, text proces-

sors, compilers, etc.

Experiments performed with real programs (and

real execution times) have demonstrated that our ap-

proach can be successfully applied in practice. We

intend to perform a more rigorous and broad assess-

ment or our approach, by applying it to large real life

programs and using fully automatic tools for estimat-

ing execution times.

Although a lot of work still remains to be done,

the preliminary results are very encouraging and we

TOWARDS FUZZY GRANULARITY CONTROL IN PARALLEL/DISTRIBUTED COMPUTING

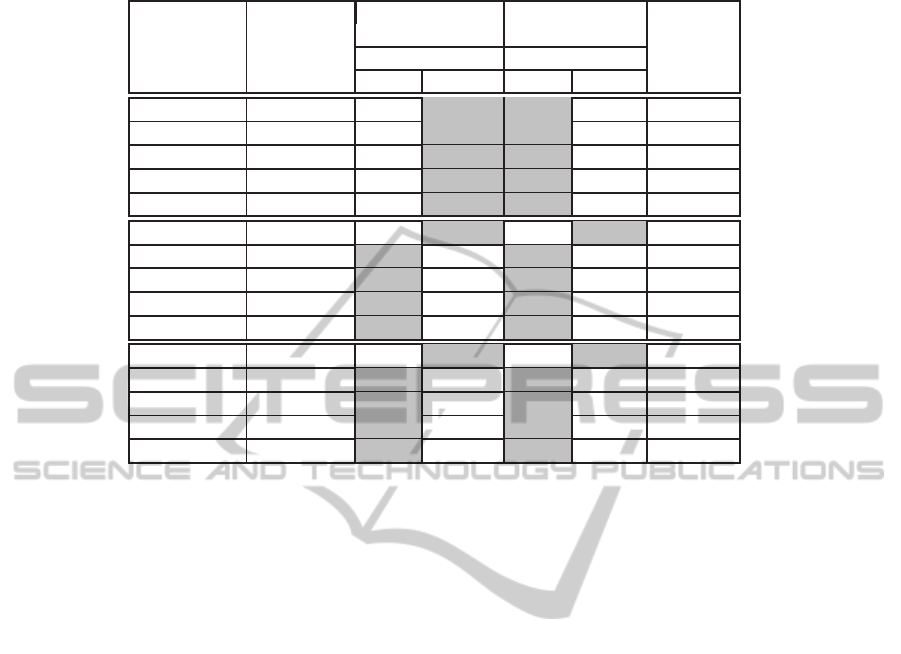
Table 6: Selected executions for real programs.

Execution Optimal

Classical Logic Fuzzy Logic

Speedup(Greater) (Quite greater)

Classical Fuzzy 2

PAR

SEQ

PAR

SEQ

qsort(250) Parallel 0 0 0.6 0.53 1.66

qsort(500) Parallel 0 0 0.6 0.53 1.74

qsort(750) Parallel 0 0 0.6 0.53 1.74

qsort(1000) Parallel 0 0 0.6 0.53 1.75

qsort(1250) Parallel 0 0 0.6 0.53 1.71

ﬁb(1) Parallel 1 1 0.53 0.53 1.0

ﬁb(3) Sequential 1 0 0.6 0.5 1.0

ﬁb(5) Parallel 1 0 0.6 0.5 1.0

ﬁb(7) Parallel 1 0 0.6 0.5 1.0

ﬁb(12) Parallel 1 0 0.6 0.5 1.0

hanoi(1) Parallel 1 1 0.53 0.53 1.0

hanoi(2) Sequential 1 0 0.6 0.5 1.0

hanoi(3) Sequential 1 0 0.6 0.5 1.0

hanoi(4) Sequential 1 0 0.6 0.5 1.0

hanoi(5) Sequential 1 0 0.61 0.5 1.0

Conditions:

PAR

is T

≤ T

SEQ

is T

≤ T

PAR

is max(gt(T

),gt(T

))

SEQ

is max(gt(T

),gt(T

))

believe that it is possible to exploit all the potential

offered by multicore systems by applying fuzzy logic

to automatic program parallelization techniques.

ACKNOWLEDGEMENTS

This research has been partially funded by the EU

7th. FP NoE S-Cube 215483, FET IST-231620 HATS,

MICINN TIN-2008-05624 DOVES and CM project

P2009/TIC/1465 PROMETIDOS. Teresa Trigo has

been supported by CAM grant CPI/0621/2008.

REFERENCES

Baldwin, J. F., Martin, T., and Pilsworth, B. (1995). Fril:

Fuzzy and Evidential Reasoning in Artiﬁcial Intelli-

gence. John Wiley & Sons.

Chassin, J. and Codognet, P. (1994). Parallel Logic Pro-

gramming Systems. Computing Surveys, 26(3):295–

336.

Debray, S. K., Lin, N.-W., and Hermenegildo, M. (1990).

Task Granularity Analysis in Logic Programs. In

Proc. of the 1990 ACM Conf. on Programming Lan-

guage Design and Implementation, pages 174–188.

ACM Press.

Guadarrama, S., Muñoz, S., and Vaucheret, C. (2004).

Fuzzy Prolog: A new Approach Using Soft Con-

straints Propagation. Fuzzy Sets and Systems, FSS,

144(1):127–150. ISSN 0165-0114.

Hermenegildo, M., Puebla, G., Bueno, F., and López-

García, P. (2005). Integrated Program Debugging,

Veriﬁcation, and Optimization Using Abstract Inter-

pretation (and The Ciao System Preprocessor). Sci-

ence of Computer Programming, 58(1–2):115–140.

Hermenegildo, M. and Rossi, F. (1995). Strict and Non-

Strict Independent And-Parallelism in Logic Pro-

grams: Correctness, Efﬁciency, and Compile-Time

Conditions. Journal of Logic Programming, 22(1):1–

45.

Hermenegildo, M. V., Bueno, F., Carro, M., López, P.,

Morales, J., and Puebla, G. (2008). An Overview

of The Ciao Multiparadigm Language and Program

Development Environment and its Design Philosophy.

In Festschrift for Ugo Montanari, number 5065 in

LNCS, pages 209–237. Springer-Verlag.

Huelsbergen, L. (1993). Dynamic Language Parallelization.

Technical Report 1178, Computer Science Dept. Univ.

of Wisconsin.

Huelsbergen, L., Larus, J. R., and Aiken, A. (1994). Using

ICFC 2010 - International Conference on Fuzzy Computation

Run-Time List Sizes to Guide Parallel Thread Cre-

ation. In Proc. ACM Conf. on Lisp and Functional

Programming.

Ishizuka, M. and Kanai, N. (1985). Prolog-ELF incorporat-

ing fuzzy logic. In IJCAI, pages 701–703.

Kaplan, S. (1988). Algorithmic Complexity of Logic Pro-

grams. In Logic Programming, Proc. Fifth Interna-

tional Conference and Symposium, (Seattle, Washing-

ton), pages 780–793.

Kruatrachue, B. and Lewis, T. (1988). Grain Size Determi-

nation for Parallel Processing. IEEE Software.

Lee, R. (1972). Fuzzy logic and the resolution principle.

Journal of the Association for Computing Machinery,

19(1):119–129.

Li, D. and Liu, D. (1990). A Fuzzy Prolog Database System.

John Wiley & Sons, New York.

López-García, P., Hermenegildo, M., and Debray, S. K.

(1996). A Methodology for Granularity Based Con-

trol of Parallelism in Logic Programs. Journal of Sym-

bolic Computation, Special Issue on Parallel Symbolic

Computation, 21(4–6):715–734.

McGreary, C. and Gill, H. (1989). Automatic Determina-

tion of Grain Size for Efﬁcient Parallel Processing.

Communications of the ACM, 32.

Mera, E., López-García, P., Carro, M., and Hermenegildo,

M. (2008). Towards Execution Time Estimation in

Abstract Machine-Based Languages. In 10th Int’l.

ACM SIGPLAN Symposium on Principles and Prac-

tice of Declarative Programming (PPDP’08), pages

174–184. ACM Press.

Muñoz-Hernández, S., Pablos-Ceruelo, V., and Strass, H.

(2009). Rfuzzy: An expressive simple fuzzy compiler.

In IWANN (1), pages 270–277.

Pablos-Ceruelo, V., Muñoz-Hernández, S., and Strass,

H. (2009a). Rfuzzy framework. Paper pre-

sented at the 18th Workshop on Logic-based Methods

in Programming Environments (WLPE2008), CoRR,

abs/0903.2188.

Pablos-Ceruelo, V., Strass, H., and Muñoz Hernández,

S. (2009b). Rfuzzy—a framework for multi-adjoint

fuzzy logic programming. In Fuzzy Information Pro-

cessing Society, 2009. NAFIPS 2009. Annual Meeting

of the North American, pages 1–6.

Rabhi, F. A. and Manson, G. A. (1990). Using Complexity

Functions to Control Parallelism in Functional Pro-

grams. Res. Rep. CS-90-1, Dept. of Computer Sci-

ence, Univ. of Shefﬁeld, England.

Strass, H., Muñoz-Hernández, S., and Pablos-Ceruelo, V.

(2009). Operational semantics for a fuzzy logic pro-

gramming system with defaults and constructive an-

swers. In IFSA/EUSFLAT Conf., pages 1827–1832.

Vaucheret, C., Guadarrama, S., and Muñoz, S. (2002).

Fuzzy Prolog: A Simple General Implementation us-

ing CLP(R). In 9th International Conference on Logic

for Programming Artiﬁcial Intelligence and Reason-

ing, Tbilisi, Georgia.

Zhong, X., Tick, E., Duvvuru, S., Hansen, L., Sastry,

A., and Sundararajan, R. (1992). Towards an Efﬁ-

cient Compile-Time Granularity Analysis Algorithm.

In Proc. of the 1992 International Conference on

Fifth Generation Computer Systems, pages 809–816.

Institute for New Generation Computer Technology

(ICOT).

TOWARDS FUZZY GRANULARITY CONTROL IN PARALLEL/DISTRIBUTED COMPUTING