ASSESSING PROGRESSIVE FILTERING TO PERFORM

HIERARCHICAL TEXT CATEGORIZATION IN PRESENCE

OF INPUT IMBALANCE

Andrea Addis, Giuliano Armano and Eloisa Vargiu

Dept. of Electrical and Electronic Engineering, University of Cagliari, Cagliari, Italy

Keywords:

Hierarchical text categorization.

Abstract:

The more the amount of available data (e.g., in digital libraries), the greater the need for high-performance

text categorization algorithms. So far, the work on text categorization has been mostly focused on “ﬂat” ap-

proaches, i.e., algorithms that operate on non-hierarchical classiﬁcation schemes. Hierarchical approaches are

expected to perform better in presence of subsumption ordering among categories. In fact, according to the

“divide et impera” strategy, they partition the problem into smaller subproblems, each being expected to be

simpler to solve. In this paper, we illustrate and discuss the results obtained by assessing the “Progressive

Filtering” (PF) technique, used to perform text categorization. Experiments, on the Reuters Corpus (RCV1-

v2) and on DZMOZ datasets, are focused on the ability of PF to deal with input imbalance. In particular,

the baseline is: (i) comparing the results to those calculated resorting to the corresponding ﬂat approach; (ii)

calculating the improvement of performance while augmenting the pipeline depth; and (iii) measuring the

performance in terms of generalization- / specialization- / misclassiﬁcation-error and unknown-ratio. Experi-

mental results show that, for the adopted datasets, PF is able to counteract great imbalances between negative

and positive examples.

1 INTRODUCTION

In the Web 2.0 age people organize large collections

of web pages, articles, or emails in hierarchies of top-

ics, or arrange a large body of knowledge in ontolo-

gies. This organization allows to focus on a speciﬁc

level of detail, ignoring specialization at lower levels

and generalization at upper levels. In this scenario,

the main goal of automatic categorization systems is

to deal with reference taxonomies in an effective and

efﬁcient way.

Furthermore, due to the increasing importance of

term polysemy for large corpora, both precision and

recall decrease as the number of categories increases

(Apt´e et al., 1994) (Yang, 1996), so that considering

categories organized in a hierarchy may help to im-

prove the overall performances. Another important

issue is concerned with the beneﬁts that a hierarchical

approach can give in real-world scenarios, typically

characterized by imbalanced data (Kotsiantis et al.,

2006). In fact, in these contexts, relevant and non rel-

evant documents (i.e., positiveand negativeexamples,

respectively) are typically imbalanced, turning classi-

ﬁers trained with the same percentage of positive and

negative examples into not adequate tools.

This paper is aimed at assessing the effectiveness

of the “Progressive Filtering” (PF) technique, applied

to text categorization in presence of input imbalance.

In its simplest setting, PF decomposes a given rooted

taxonomy into pipelines, one for each path that exists

between the root and any given node of the taxonomy,

so that each pipeline can be tuned in isolation. To this

end, a Threshold Selection Algorithm (TSA) has been

devised, aimed at ﬁnding a sub-optimal combination

of thresholds for each pipeline.

The rest of the paper is organized as follows: in

Section 2, a brief overview of selected related work

on both hierarchical text categorization and input im-

balance is presented. Sections 3 describes progressive

ﬁltering. In Section 4, the adopted threshold selection

algorithm is presented. Experiments and results are

illustrated in Section 5. Section 6 ends the paper with

conclusions and future work.

Addis A., Armano G. and Vargiu E..

ASSESSING PROGRESSIVE FILTERING TO PERFORM HIERARCHICAL TEXT CATEGORIZATION IN PRESENCE OF INPUT IMBALANCE.

DOI: 10.5220/0003066300140023

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 14-23

ISBN: 978-989-8425-28-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

2.1 Hierarchical Text Categorization

In the last years several researchers have investigated

the use of hierarchies for text categorization, which is

also the main focus of our proposal.

Until the mid-1990s researchers mostly ignored

the hierarchical structure of categories that occur in

several domains. In 1997, Koller and Sahami (Koller

and Sahami, 1997) carried out the ﬁrst proper study

on hierarchical text categorization on the Reuters-

22173 collection. Documents were classiﬁed accord-

ing to the given hierarchy by ﬁltering them through

the single best-matching ﬁrst-level class and then

sending them to the appropriatesecond level. This ap-

proach showed that hierarchical models perform well

when a small number of features per class is used. In

fact, no advantages were found using the hierarchical

model for large numbers of features.

McCallum et al. (McCallum et al., 1998) pro-

posed a method based on na¨ıve Bayes. The authors

compare two techniques: (i) exploring all possible

paths in the given hierarchy, and (ii) greedily selecting

at most two branches according to their probability, as

done in (Koller and Sahami, 1997). Results show that

the latter is more error prone while computationally

more efﬁcient.

Mladeni´c (Mladenic and Grobelnik, 1998) used

the hierarchical structure to decompose a problem

into a set of subproblems, correspondingto categories

(i.e., the nodes of the hierarchy). For each subprob-

lem, a na¨ıve Bayes classiﬁer is generated, considering

examples belonging to the given category, including

all examples classiﬁed in its subtrees. The classiﬁ-

cation applies to all nodes in parallel, a document is

passed down to a category only if the posterior prob-

ability for that category is higher than a user-deﬁned

threshold.

D’Alessio (D’Alessio et al., 2000) proposed a sys-

tem in which, for a given category, the classiﬁcation

is based on a weighted sum of feature occurrences

that should be greater than the category threshold.

Both single and multiple classiﬁcations are possible

for each document to be tested. The classiﬁcation of

a document proceeds top-down possibly through mul-

tiple paths. An innovative contribution of this work is

the possibility of restructuring a given hierarchy or

building a new one from scratch.

Dumais and Chen (Dumais and Chen, 2000) used

the hierarchical structure for two purposes: (i) train-

ing several SVMs, one for each intermediate node,

and (ii) classifying documents by combining scores

from SVMs at different levels. The sets of positive

and negative examples are built considering docu-

ments that belong to categories at the same level, and

different feature sets are built, one for each category.

Several combination rules have also been assessed.

In the work by Ruiz and Srinivasan (Ruiz and

Srinivasan, 2002) a variant of the Hierarchical Mix-

ture of Experts model is used. A hierarchical classiﬁer

combining several neural networks is also proposed in

(Weigend et al., 1999).

Gaussier et al. (Gaussier et al., 2002) proposed a

hierarchical generative model for textual data, where

words may be generated by topic speciﬁc distribu-

tions at any level in the hierarchy. This model is

aimed at clustering documentsin preset- or (automati-

cally) generated-hierarchies,as well as at categorizing

new documents in an existing taxonomy.

In (Rousu et al., 2005) a kernel-based algorithm

for hierarchical text classiﬁcation has been presented.

Documents are allowed to belong to more than one

category at a time. The classiﬁcation model is a vari-

ant of the Maximum Margin Markov Network frame-

work, where the taxonomy is represented as a Markov

tree equipped with an exponential family deﬁned on

the edges. Experiments showed that the proposed al-

gorithm can feasibly optimize training sets of thou-

sands of examples and taxonomies consisting of hun-

dreds of nodes.

Ceci and Malerba (Ceci and Malerba, 2007) pre-

sented a comprehensive study on hierarchical classi-

ﬁcation of web documents. They extend a previous

work (Ceci and Malerba, 2003) considering: (i) hi-

erarchical feature selection mechanisms; (ii) a na¨ıve

Bayes algorithm aimed at avoiding problems related

to different document lengths; (iii) the validation of

their framework for a probabilistic SVM-based clas-

siﬁer; and (iv) an automated threshold selection algo-

rithm.

More recently, in (Esuli et al., 2008), the authors

proposed a multi-label hierarchical text categorization

algorithm consisting of a hierarchical variant of AD-

ABOOST.MH, a well-known member of the family

of “boosting” learning algorithms.

Bennett et al. (Bennett and Nguyen, 2009) stud-

ied the problem of the error propagation under the as-

sumption that a mistake is made at “high” nodes in

the hierarchy, as well as the problem of dealing with

increasingly complex decision surfaces.

Brank et al. (Brank et al., 2010) dealt with the

problem of classifying textual documents into a top-

ical hierarchy of categories. They construct a coding

matrix gradually, one column at a time, each new col-

umn being deﬁned in a way that the corresponding

binary classiﬁer attempts to correct the most common

mistakes of the current ensemble of binary classiﬁers.

ASSESSING PROGRESSIVE FILTERING TO PERFORM HIERARCHICAL TEXT CATEGORIZATION IN

PRESENCE OF INPUT IMBALANCE

The goal is to achieve good performance while keep-

ing reasonably low the number of binary classiﬁers.

2.2 The Input Imbalance Problem

Japkowicz (Japkowicz, 2000) studied the class im-

balance problem. In particular, for binary classiﬁ-

cation, the author studied the problem related to do-

mains in which one class is represented by a large

number of examples whereas the other is represented

by only a few. High imbalance occurs in real-world

domains where the decision system is aimed at de-

tecting a rare but important case (Kotsiantis et al.,

2006). The problem of imbalance has got more and

more emphasis in recent years. Imbalanced data sets

exist in many real-world domains, such as spotting

unreliable telecommunication customers, detection of

oil spills in satellite radar images, learning word pro-

nunciations, text classiﬁcation, detection of fraudu-

lent telephone calls, information retrieval and ﬁlter-

ing tasks, and so on (Wu and Chang, 2003) (Yan

et al., 2003). A number of solutions to the class

imbalance problem have been proposed both at the

data- and algorithmic-level. Data-level solutions in-

clude many different forms of resampling such as ran-

dom oversampling with replacement, random under-

sampling, directed oversampling, directed undersam-

pling, oversampling with informed generation of new

samples, and combinations of the above techniques

(Kubat and Matwin, 1997) (Chawla et al., 2002) (Kot-

siantis and Pintelas, 2003). To counteract the class

imbalance, algorithmic-levelsolutions include adjust-

ing the costs of the various classes, adjusting the

decision threshold, and adopting recognition-based

rather than discrimination-based learning. Hybrid ap-

proaches have also been used to handle the class im-

balance problem.

3 PROGRESSIVE FILTERING IN

TEXT CATEGORIZATION

In this work, we are interested in studying how to

cope with input imbalance in a hierarchical text cate-

gorization setting. The underlying motivation is that,

in real world applications, the ratio between inter-

esting and uninteresting documents is typically very

low, so that classiﬁers trained with a balanced training

set are inadequate to deal with those environments.

To this end, we perform the training activity in two

phases. First, each classiﬁer is trained by using a bal-

anced dataset. Then, a threshold selection algorithm

is applied and thresholds are calculated taking into ac-

count the input imbalance.

A theoretical assessment of the approach is be-

yond the scope of this paper, the interested reader

could refer to (Armano, 2009) for further details.

A way to implement Progressive Filtering (PF)

consists of unfolding the given taxonomy into

pipelines of classiﬁers, as depicted in Figure 1. Each

node of the pipeline is a binary classiﬁer able to rec-

ognize whether or not an input belongs to the corre-

sponding class (i.e., to the corresponding node of the

taxonomy).

Figure 1: A taxonomy and its corresponding pipelines.

In principle, PF could be applied to classify any

kind of items, including images, audios, videos, tex-

tual documents. As in this paper we are interested in

applying PF to hierarchical text categorization, only

textual documents (documents for short, hereinafter)

have been considered.

Given a taxonomy, where each node represents a

classiﬁer entrusted with recognizing all correspond-

ing positive inputs (i.e., interesting documents), each

input traverses the taxonomy as a “token”, starting

from the root. If the current classiﬁer recognizes it

as positive, the token is passed to all its children (if

any), and so on. A typical result consists of activating

one or more branches within the taxonomy, in which

the corresponding classiﬁers have been activated by

the given token.

Let us note that, partitioning the taxonomy in

pipelines gives rise to a set of new classiﬁers, each

represented by a pipeline. For instance, the taxonomy

depicted in Figure 1 gives rise to six pipelines.

Finally, let us note that the proposed approach

performs a sort of “ﬂattening” though preserving the

information about the hierarchical relationships em-

bedded in a pipeline. For instance, the pipeline

i actually represents the classiﬁer C

, al-

though the information about the existing subsump-

tion relationships, i.e., C

≤ C

, is preserved.

4 THE THRESHOLD SELECTION

ALGORITHM

As we know from classical text categorization, given

a set of documents D and a set of labels C, a function

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

CSV

: D → [0,1] exists for each c

∈ C. The behavior

of c

is controlled by a threshold θ

, responsible for

relaxing or restricting the acceptance rate of the cor-

responding classiﬁer. Let us recall that, given d ∈ D,

CSV

(d) ≥ θ

is interpreted as a decision to categorize

d under c

, whereas CSV

(d) < θ

is interpreted as a

decision not to categorize d under c

In PF, let us still assume that CSV

exists for each

∈ C, with the same semantics adopted in the clas-

sical case. Considering a pipeline π, composed by n

classiﬁers, the acceptance policy strictly depends on

the vector of thresholds θ

= hθ

,θ

,··· ,θni that em-

bodies the thresholds of all classiﬁers in π. In order to

categorize d under π, the following constraint must be

satisﬁed: ∀k = 1..n, CSV

(d) ≥ θ

. On the contrary, d

is not categorized under c

in the event that a classi-

ﬁer in π rejects it. In so doing, a classiﬁer may have

different behaviors, depending on which pipeline it is

embedded. As a consequence, each pipeline can be

considered in isolation from the others. For instance,

given π

= hC

i and π

= hC

i, the clas-

siﬁer C

is not compelled to have the same threshold

in π

and in π

(the same holds for C

In PF, given an utility function

, we are interested

in ﬁnding an effective (and computationally “light”)

way to reach a sub-optimum in the task of determin-

ing the best vector of thresholds. To this end, for

each pipeline π a sub-optimal combination of thresh-

olds is searched for, considering the actual ratio be-

tween positive and negative examples, which in turn

depends on the given scenario. Unfortunately, ﬁnd-

ing the best acceptance thresholds is a difﬁcult task.

In fact, exhaustively trying each possible combination

of thresholds (brute-force approach) is unfeasible, the

number of thresholds being virtually inﬁnite. How-

ever, the brute-force approach can be approximated

by deﬁning a granularity step that requires to assess

only a ﬁnite number of points in a range[0, 1] in which

the thresholds are permitted to vary with step δ. This

“relaxed” brute force algorithm (RBF for short) for

calibrating thresholds would be very helpful in the

task of ﬁnding a sub-optimal solution, although still

too heavy from a computational point of view. Thus,

to perform PF we adopt a Threshold Selection Algo-

rithm (namely, TSA) devised to deal with this prob-

lem, which maintains the capability of ﬁnding a near-

optimum solution characterized by a low time com-

plexity (Addis et al., 2010).

Searching for a sub-optimal combination of

thresholds in a pipeline can be actually viewed as the

problem of ﬁnding a maximum in a utility function F

Different utility functions (e.g., precision, recall, F

user-deﬁned) can be adopted, depending on the constraint

imposed by the underlying scenario.

that depends on the corresponding thresholds θ:

∗

= argmax

F(θ) (1)

Unfortunately, the task of threshold calibration

is characterized by a high time complexity. Hence,

given the utility function F, we are interested in ﬁnd-

ing an effective way to reach a sub-optimum in the

task of determining which are the best thresholds,

while taking into account the actual ratio between

positive and negative examples that concerns with the

given scenario.

Bearing in mind that the lower the threshold the

less restrictive the classiﬁer, we can build a greedy

bottom-up algorithm for selecting decision threshold

that relies on two functions:

• repair (R ), which operates on a classiﬁer C

by increasing or decreasing its threshold –i.e.,

R (up,C) and, R (down,C), respectively– until

the selected utility function reaches and maintains

a local maximum.

• calibrate (C ), which operates going downwards

from the given classiﬁer to its offspring by repeat-

edly calling R . It is intrinsically recursive and at

each step it calls R to calibrate the current classi-

ﬁer.

Given a pipeline π = hC

,··· ,C

i, where L is its

depth,

TSA

is then deﬁned as follows (all thresholds

are initially set to zero):

TSA(π) := fork = L downto1doC (up,C

) (2)

which indicates that C is applied to each node of the

pipeline, starting from the leaf (k = L).

Under the assumption that p is a structure that

contains all information about a pipeline, including

the corresponding vector of thresholds and the utility

function to be optimized, the pseudo-code of TSA is:

function TSA(p:pipeline):

for k:=1 to p.length

do p.thresholds[i] = 0

for k:=p.length downto 1

do Calibrate(up,p,k)

return p.thresholds

end TSA

The

Calibrate

function is deﬁned as follows:

C (up,C

) := R (up,C

), k = L

C (up,C

) := R (up,C

) + C (down,C

k+1

), k < L

(3)

and

ASSESSING PROGRESSIVE FILTERING TO PERFORM HIERARCHICAL TEXT CATEGORIZATION IN

PRESENCE OF INPUT IMBALANCE

C (down,C

) := R (down,C

), k = L

C (down,C

) := R (down,C

) + C (up,C

k+1

), k < L

(4)

where the + operator actually denotes a sequence op-

erator (meaning that in the formula a + b action a is

performed before action b). In pseudo-code:

function Calibrate(dir:{up,down}, p:pipeline,

level:integer):

Repair(dir,p,level)

if level < p.length

then Calibrate(toggle(dir),p,level+1)

end Calibrate

where

toggle

is a function that reverses the current

direction, and

Repair

is deﬁned as:

function Repair(dir:{up,down}, p:pipeline,

level:integer):

delta := (dir = up) ? p.delta : -p.delta

best_threshold := p.thresholds[level]

max_uf := p.utility_function()

uf := max_uf

while uf >= max_uf * 0.8 and

p.thresholds[level] in [0,1]

do p.thresholds[level] :=

p.thresholds[level] + delta

uf := p.utility_function()

if uf < max_uf then continue

max_uf := uf

best_threshold := p.thresholds[level]

p.thresholds[level] := best_threshold

end Repair

The factor 0.8, experimentally calculated, is used

to limit the impact of local minimums during the

search.

After calculating the sub-optimal combination of

thresholds for a given imbalance, the pipelines are

ready to be used in the corresponding scenario. Let

us note, here, that this combination depends on both

the adopted dataset and the actual input imbalance. In

fact, as noted in (Lewis, 1995), different goals for the

system lead to different optimal behaviors.

As for the time complexity of TSA, to simplify

the problem, let us deﬁne a granularity step that re-

quires to visit only a ﬁnite number of points in a

range [ρ

min

,ρ

max

], 0 ≤ ρ

min

< ρ

max

≤ 1, in which

the thresholds could vary with step δ. Therefore,

p = ⌊δ

−1

· (ρ

max

− ρ

min

)⌋ being the maximum num-

ber of points to be checked for each classiﬁer in a

pipeline and L being the length of the pipeline, the

average time of TSA, T(TSA), is proportional to

(L + L

) · p · (ρ

max

− ρ

min

), which implies that TSA

has complexity O(L

). Hence, the time complexity is

quadratic with the number of classiﬁers embedded by

a pipeline. As already noted, a comparison between

TSA and the brute-force approach is unfeasible, the

elements of the threshold vector being real numbers.

Nevertheless, experimental results show that the ef-

fectiveness of TSA is almost identical to the one ob-

tained by running RBF, in which only p points are

checked for each classiﬁer in a pipeline. Note that

the average time of RBF, T(RBF), is proportional to

, which in turns implies that its computational com-

plexity is O(p

It is also important to note that, due to the enor-

mous computational time that can be reached, the

RBF approach should be applied in practice only by

setting p to a value much lower than the one appli-

cable with TSA. For instance, with a ratio of 10

−2

i.e., p

RBF

= 20 and p

TSA

= 2000, T(RBF) ∝ 160,000

and T(TSA) ∝ 20, 000. In other words, TSA is still

8 times faster than RBF, even considering ρ

max

= 1

and ρ

min

= 0, while ensuring a better result due to the

higher granularity.

5 EXPERIMENTS AND RESULTS

Experiments have been performed to validate the pro-

posed approach with respect to the impact of PF in

the input imbalance. To this end, three series of ex-

periments have been performed: ﬁrst, performances

calculated resorting to PF have been compared with

those calculated by resorting to the corresponding ﬂat

approach. Then, PF has been tested to assess the

improvement of performances while augmenting the

pipeline depth. Finally, performances have been cal-

culated in terms of generalization- / specialization- /

misclassiﬁcation-error and unknown-ratio.

Furthermore, to show that the overall perfor-

mances of PF are not worsened by the adoption of

TSA vs. RBF, we performed further experiments

aimed at comparing the performance of PF obtained

by applying TSA vs. those obtained by applying RBF.

We are also currentlyperforming newexperiments

aimed at comparing the proposed approach with state-

of-the-art systems and techniques. Nevertheless, as

the paper is more concerned with studying how input

imbalance affects performance in text categorization,

we decided to focus on experiments that compare the

effectiveness of the proposed hierarchical approach

vs. the ﬂat one.

Experiments have been performed by customizing

for this speciﬁc task X.MAS (Addis et al., 2008), a

generic multiagent architecture built upon JADE (Bel-

lifemine et al., 2007), devised to make easier the im-

plementation of information retrieval and information

ﬁltering applications.

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

5.1 The Adopted Datasets

The two corpora selected for this study are the bench-

mark datasets Reuters Corpus Volume I (RCV1-v2)

(Lewis et al., 2004) and DMOZ, the collection of

HTML documents referenced in a web directory de-

veloped in the Open Directory Project (ODP). The

corpora differ considerably in the size of the training

set, in the hierarchical structure of categories, as well

as in the procedure adopted for the classiﬁcation of

documents. For the sake of completeness, a brief de-

scription of such collections is reported.

As for the Reuters corpora, we adopted the sec-

ond version of the Reuters Corpus dataset (RCV1-

v2) (Lewis et al., 2004). In this corpus, stories

have been coded into four hierarchical groups: Cor-

porate/Industrial (CCAT), Economics (ECAT), Gov-

ernment/Social (GCAT), and Markets (MCAT). Al-

though the complete list consists of 126 categories,

only part of them were used for testing the proposed

hierarchical approach. The total number of codes ac-

tually assigned to the data is 93, whereas the overall

number of documents is about 803,000, each docu-

ment belonging to at least one category and (on aver-

age) to 3.8 categories.

As for DMOZ

, to be able to explore the effects of

the taxonomy depth on PF performances, we selected

17 categories with a maximum depth of 5. In so do-

ing, each category includes at least 300 documents.

The corresponding training set includes a subset of

the 136,000 documents, each belonging to one cate-

gory.

5.2 Evaluation Measures

To evaluate the performances of PF, several measures

have been considered.

First, the approach is validated resorting to a con-

ventional metric for calculating the performances of

a text categorization system –i.e., macro-averaging.

Macro-averaged scores are calculated by ﬁrst calcu-

lating precision and recall for each category and then

taking their average. In other words, macro-averaging

ﬁrst evaluatesP and R “locally” for each category, and

then “globally” by averaging over the results of the

different categories. In symbols:

∑

i=1

(5)

∑

i=1

(6)

where the “M” superscript stands for macroaveraging.

http://www.dmoz.org

To evaluate the performances of the approach, we

also applied F

, obtained from the general deﬁnition

of F

by imposing the same degree of importance for

P and R. In symbols:

(1+ β

)P· R

P+ R

(7)

= F

β=1

2PR

P+ R

(8)

Then, the approach is validated using four ad-

ditional evaluation measures, deﬁned in (Ceci and

Malerba, 2007):

• misclassiﬁcation error, i.e., the percentage of doc-

uments misclassiﬁed in a category not related to

the correct category in the hierarchy;

• generalization error, i.e., the percentage of docu-

ments misclassiﬁed in a supercategory of the cor-

rect one;

• specialization error, i.e., the percentage of docu-

ments misclassiﬁed in a subcategory of the correct

one;

• unknown ratio, i.e., the percentage of rejected

documents.

5.3 Results

The main issue being investigated is the effectiveness

of the proposed approach with respect to ﬂat clas-

siﬁcation. In order to make a fair comparison, the

same classiﬁcation system has been adopted, i.e., a

classiﬁer based on the wk-NN technology (Cost and

Salzberg, 1993). The motivation for the adoption of

this particular technique stems from the fact that it

does not require speciﬁc training and is very robust

with respect to noisy data. In fact, as demonstrate in

(Takigawa et al., 2005) wk-NN-based approaches can

reduce the error rate due to robustness against out-

liers.

During the training activity, ﬁrst, each classiﬁer

is trained with a balanced data set of 1000 docu-

ments for Reuters and 100 for DMOZ, by using 200

(TFIDF) features selected in accordance with their

information gain. For any given node, the training

set contains documents taken from the correspond-

ing subtree and documents of the sibling subtrees –as

positive and negative examples, respectively. Then,

the best thresholds are selected. Both the thresholds

of the pipelines and of the ﬂat classiﬁers have been

chosen by adopting F

as utility function

. As for

pipelines, we used a step δ of 10

−4

for TSA.

The utility function can be adopted depending on the

constraint imposed by the given scenario. For instance, F

is suitable if one wants to give equal importance to precision

and recall.

ASSESSING PROGRESSIVE FILTERING TO PERFORM HIERARCHICAL TEXT CATEGORIZATION IN

PRESENCE OF INPUT IMBALANCE

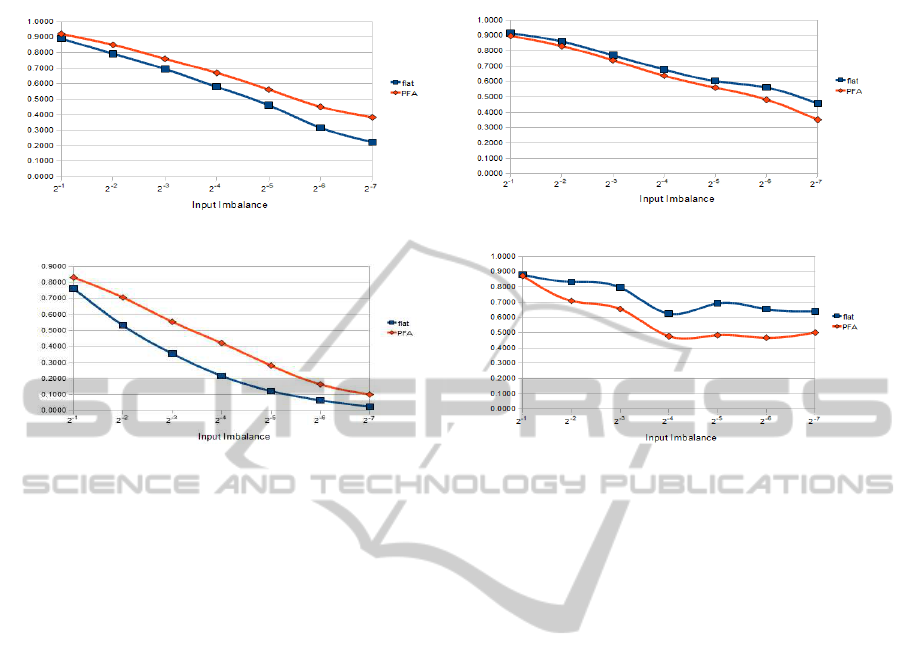
Precision - Reuters dataset

Recall - Reuters dataset

Precision - DMOZ dataset Recall - DMOZ dataset

Figure 2: Comparison of precision and recall between PF and ﬂat classiﬁcation.

Experiments have been performed by assessing

the behavior of the proposed hierarchical approach

in presence of different ratios of positive examples

versus negative examples, i.e., from 2

−1

to 2

−7

. We

considered only pipelines that end with a leaf node of

the taxonomy. Accordingly, for the ﬂat approach, we

considered only classiﬁers that correspond to a leaf.

PF vs Flat Classiﬁcation. Figure 2 shows macro-

averaging of precision and recall for Reuters and

DMOZ datasets. Precision and recall have been cal-

culated for both the ﬂat classiﬁers and the pipelines

by varying the input imbalance. As pointed out by

experimental results (for precision), the distributed

solution based on pipelines has reported better

results than those obtained with the ﬂat model. On

the contrary, results on recall are worse than those

obtained with the ﬂat model.

Improving Performance along the Pipeline. Figure

3 shows the performance improvements in terms

of F

on Reuters and DMOZ datasets of the pro-

posed approach with respect to the ﬂat one. The

improvement has been calculated in percentage

with the formula (F

(pipeline) − F

( flat)) × 100.

Experimental results –having the adopted taxonomies

a maximum depth of ﬁve– show that PF performs

always better than the ﬂat approach. Nevertheless,

as for DMOZ, let us note that these results depend

on the amount of examples of the categories under

analysis. This is an unavoidable side effect related

to the decision of performing experiments with

pipelines of length ﬁve.

Hierarchical Metrics. Figure 4 depicts the re-

sults obtained varying the imbalance on Reuters

and DMOZ datasets. Analyzing the results, it is

easy to note that the generalization-error and the

misclassiﬁcation-error grow with the imbalance,

whereas the specialization-error and the unknown-

ratio decrease. As for the generalization-error, it

depends on the overall number of false negatives

(FNs), the greater the imbalance the greater the

amount of FNs. Hence, the generalization-error

increases with the imbalance. In presence of input

imbalance, the trend of the generalization-error is

similar to the trend of the recall measure. As for the

specialization-error, it depends on the overall number

of false positives (FPs), the greater the imbalance, the

lower the amount of FPs. Hence, the specialization-

error decreases with the imbalance. In presence of

input imbalance, the trend of the specialization-error

is similar to the trend of the precision. As for the

unknown-ratio and misclassiﬁcation-error, let us

point out that an imbalance between positive and

negative examples can be suitably dealt with by

exploiting the ﬁltering effect of classiﬁers in the

pipeline. As ﬁnal remark, let us note that different

utility functions can be adopted, depending on which

aspect or unwanted effect one wants to improve

or mitigate. For instance, recall could be adopted

as utility function to reduce the overall number of

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

Reuters dataset

DMOZ dataset

Figure 3: Performance improvement.

Reuters dataset

DMOZ dataset

Figure 4: Hierarchical measures.

Table 1: TSA vs. RBF: F

in presence of input imbalance.

Input imbalance F

(RBF) F

(TSA)

−1

0.830 0.835

−2

0.722 0.733

−3

0.619 0.632

−4

0.497 0.515

−5

0.404 0.428

−6

0.323 0.345

−7

0.245 0.273

FNs. In fact, optimizing recall implies to accept as

positive documents that are in fact true negatives

(TNs). In this way, the unknown-ratio (which

depends on the amount of FNs) decreases, whereas

the misclassiﬁcation-error (which depends on the

amount of FPs) increases.

TSA vs. RBF. Experiments have been performed

by assessing the behavior of PF in terms of F

presence of different ratios of positive examples vs.

negative examples –i.e., from 2

−1

to 2

−7

. Results,

summarized in Table 1, show that the performance

of TSA is always better than the one obtained with

RBF. This is due to the fact that, as previously pointed

out, TSA has been used with a higher granularity (i.e.,

RBF

TSA

= 20/2000 = 10

−2

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we made experiments on PF to investi-

gate how the ratio between positive and negative ex-

amples affects the performances of a classiﬁer sys-

tem and how these performances can be improved by

adopting PF instead of a classical ﬂat approach. Re-

sults show that the proposed approach is able to deal

with high imbalance between negative and positive

examples.

As for the future work, several issues are currently

under investigation. In particular, we are currently

performing new experiments aimed at comparing the

proposed approach with state-of-the-art systems and

techniques. Moreover, we are interested in: (i) in-

vestigating the whole taxonomy instead of the corre-

sponding set of pipelines; (ii) adopting and calculat-

ing further metrics to assess the performances of PF;

(iii) testing PF on further datasets, such as TREC or

MeSH.

REFERENCES

Addis, A., Armano, G., and Vargiu, E. (2008). From a

generic multiagent architecture to multiagent informa-

tion retrieval systems. In AT2AI-6, Sixth International

ASSESSING PROGRESSIVE FILTERING TO PERFORM HIERARCHICAL TEXT CATEGORIZATION IN

PRESENCE OF INPUT IMBALANCE

Workshop, From Agent Theory to Agent Implementa-

tion, pages 3–9.

Addis, A., Armano, G., and Vargiu, E. (2010). Experimen-

tal assessment of a threshold selection algorithm for

tuning classiﬁers in the ﬁeld of hierarchical text cat-

egorization. In Proceedings of 17th RCRA Interna-

tional Workshop on Experimental evaluation of algo-

rithms for solving problems with combinatorial explo-

sion.

Apt´e, C., Damerau, F., and Weiss, S. M. (1994). Automated

learning of decision rules for text categorization. ACM

Transactions on Information Systems, 12(3):233–251.

Armano, G. (2009). On the progressive ﬁltering approach

to hierarchical text categorization. Technical report,

DIEE - University of Cagliari.

Bellifemine, F., Caire, G., and Greenwood, D. (2007). De-

veloping Multi-Agent Systems with JADE (Wiley Se-

ries in Agent Technology). John Wiley and Sons.

Bennett, P. N. and Nguyen, N. (2009). Reﬁned experts:

improving classiﬁcation in large taxonomies. In SI-

GIR ’09: Proceedings of the 32nd international ACM

SIGIR conference on Research and development in

information retrieval, pages 11–18, New York, NY,

USA. ACM.

Brank, J., Mladenic, D., and Grobelnik, M. (2010). Large-

scale hierarchical text classiﬁcation using svm and

coding matrices. In Large-Scale Hierarchical Clas-

siﬁcation Workshop.

Ceci, M. and Malerba, D. (2003). Hierarchical classiﬁca-

tion of HTML documents with WebClassII. In Sebas-

tiani, F., editor, Proceedings of ECIR-03, 25th Euro-

pean Conference on Information Retrieval, pages 57–

72. Berlin Heidelberg NewYork: Springer.

Ceci, M. and Malerba, D. (2007). Classifying web doc-

uments in a hierarchy of categories: a comprehen-

sive study. Journal of Intelligent Information Systems,

28(1):37–78.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). SMOTE: Synthetic minority over-

sampling technique. Journal of Artiﬁcial Intelligence

Research, 16:321–357.

Cost, W. and Salzberg, S. (1993). A weighted nearest

neighbor algorithm for learning with symbolic fea-

tures. Machine Learning, 10:57–78.

D’Alessio, S., Murray, K., and Schiafﬁno, R. (2000). The

effect of using hierarchical classiﬁers in text catego-

rization. In Proceedings of of the 6th International

Conference on Recherche dInformation Assiste par

Ordinateur (RIAO), pages 302–313.

Dumais, S. T. and Chen, H. (2000). Hierarchical classiﬁca-

tion of Web content. In Belkin, N. J., Ingwersen, P.,

and Leong, M.-K., editors, Proceedings of SIGIR-00,

23rd ACM International Conference on Research and

Development in Information Retrieval, pages 256–

263, Athens, GR. ACM Press, New York, US.

Esuli, A., Fagni, T., and Sebastiani, F. (2008). Boosting

multi-label hierarchical text categorization. Inf. Retr.,

11(4):287–313.

Gaussier, E., Goutte, C., Popat, K., and Chen, F. (2002).

A hierarchical model for clustering and categorising

documents. In Proceedings of the 24th BCS-IRSG Eu-

ropean Colloquium on IR Research, pages 229–247,

London, UK. Springer-Verlag.

Japkowicz, N. (2000). Learning from imbalanced data sets:

a comparison of various strategies. In AAAI Workshop

on Learning from Imbalanced Data Sets.

Koller, D. and Sahami, M. (1997). Hierarchically classi-

fying documents using very few words. In Fisher,

D. H., editor, Proceedings of ICML-97, 14th Interna-

tional Conference on Machine Learning, pages 170–

178, Nashville, US. Morgan Kaufmann Publishers,

San Francisco, US.

Kotsiantis, S., Kanellopoulos, D., and Pintelas, P. (2006).

Handling imbalanced datasets: a review. GESTS In-

ternational Transactions on Computer Science and

Engineering, 30:25–36.

Kotsiantis, S. and Pintelas, P. (2003). Mixture of expert

agents for handling imbalanced data sets. Ann Math

Comput Teleinformatics, 1:46–55.

Kubat, M. and Matwin, S. (1997). Addressing the curse of

imbalanced training sets: One-sided selection. In In

Proceedings of the Fourteenth International Confer-

ence on Machine Learning, pages 179–186. Morgan

Kaufmann.

Lewis, D., Yang, Y., Rose, T., and Li, F. (2004). RCV1:

A new benchmark collection for text categorization

research. Journal of Machine Learning Research,

5:361–397.

Lewis, D. D. (1995). Evaluating and optimizing au-

tonomous text classiﬁcation systems. In SIGIR ’95:

Proceedings of the 18th annual international ACM SI-

GIR conference on Research and development in in-

formation retrieval, pages 246–254, New York, NY,

USA. ACM.

McCallum, A. K., Rosenfeld, R., Mitchell, T. M., and Ng,

A. Y. (1998). Improving text classiﬁcation by shrink-

age in a hierarchy of classes. In Shavlik, J. W., edi-

tor, Proceedings of ICML-98, 15th International Con-

ference on Machine Learning, pages 359–367, Madi-

son, US. Morgan Kaufmann Publishers, San Fran-

cisco, US.

Mladenic, D. and Grobelnik, M. (1998). Feature selection

for classiﬁcation based on text hierarchy. In Text and

the Web, Conference on Automated Learning and Dis-

covery CONALD-98.

Rousu, J., Saunders, C., Szedmak, S., and Shawe-Taylor,

J. (2005). Learning hierarchical multi-category text

classiﬁcation models. In ICML ’05: Proceedings of

the 22nd international conference on Machine learn-

ing, pages 744–751, New York, NY, USA. ACM.

Ruiz, M. E. and Srinivasan, P. (2002). Hierarchical text cat-

egorization using neural networks. Information Re-

trieval, 5(1):87–118.

Takigawa, Y., Hotta, S., Kiyasu, S., and Miyahara, S.

(2005). Pattern classiﬁcation using weighted aver-

age patterns of categorical k-nearest neighbors. In

Proceedings of the 1th International Workshop on

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

Camera-Based Document Analysis and Recognition,

pages 111–118.

Weigend, A. S., Wiener, E. D., and Pedersen, J. O. (1999).

Exploiting hierarchy in text categorization. Informa-

tion Retrieval, 1(3):193–216.

Wu, G. and Chang, E. Y. (2003). Class-boundary align-

ment for imbalanced dataset learning. In In ICML

2003 Workshop on Learning from Imbalanced Data

Sets, pages 49–56.

Yan, R., Liu, Y., Jin, R., and Hauptmann, A. (2003). On

predicting rare classes with svm ensembles in scene

classiﬁcation. In Acoustics, Speech, and Signal Pro-

cessing, 2003. Proceedings. (ICASSP ’03). 2003 IEEE

International Conference on, volume 3, pages III–21–

4 vol.3.

Yang, Y. (1996). An evaluation of statistical approaches

to medline indexing. In Proceedings of the American

Medical Informatic Association (AMIA), pages 358–

362.

ASSESSING PROGRESSIVE FILTERING TO PERFORM HIERARCHICAL TEXT CATEGORIZATION IN

PRESENCE OF INPUT IMBALANCE