
BROADER PERCEPTION FOR LOCAL COMMUNITY
IDENTIFICATION
F. T. W. (Frank) Koopmans and Th. P. (Theo) van der Weide
Institute for Computing and Information Sciences, Radboud University, Nijmegen, The Netherlands
Keywords:
Networks, Communities, Clustering, Local.
Abstract:
A local community identification algorithm can identify the network community of a given start node without
knowledge of the entire network. Such algorithms only consider nodes within or directly adjacent to the
local community. Therefore a local algorithm is more effective than an algorithm that partitions the entire
network when only a small portion of a large network is of interest or when it is difficult to obtain information
about the network (such as the world wide web). However, local algorithms cannot deliver the same quality
as their global counterparts that use the entire network. We propose an improvement to local community
identification algorithms that will decrease the gap between relevant network knowledge of global and local
methods. Benchmarks on synthetic networks show our approach increases the quality of locally identified
communities in general and a decrease of the dependency on specific source nodes.
1 INTRODUCTION
The science of complex systems is a popular interdis-
ciplinary field of research. Using a network to repre-
sent the elements and interactions in a complex net-
work is a commonly used tool to study complex sys-
tem phenomena (Strogatz, 2001; Albert and Barabasi,
2002). Such analysis is done (among others) on pro-
tein networks, social networks and (parts of) the in-
ternet (Newman, 2003; Palla et al., 2007).
Complex systems, and thus their representation as
a network, often exhibit an a-priori unknown struc-
ture of building blocks with varying functions. These
blocks are represented in the network as sets of nodes
that are densely connected and have relatively few
connections to the rest of the network. Such build-
ing blocks are referred to as modules, communities or
clusters. Identifying and observing such communities
may lead to a greater understanding of the structure
and functioning of a complex system. Many different
techniques for identifying all communities within a
network, with varying computational costs and accu-
racy, have been developed (Danon et al., 2005; Lan-
cichinetti and Fortunato, 2009).
In some cases one would rather identify a specific
community instead of all communities in the entire
network in order to reduce the amount of information
that needs to be processed or acquired. For example,
finding the community around a given website on the
internet or finding all friends of a specific person in a
social network. In such cases there should be no need
to process the entire network. A local community is a
community in the network identified by starting from
a start node and using only information from the con-
text of the local community to identify local commu-
nity members. Thus no knowledge of the entire net-
work is required.
There are many different approaches to local com-
munity identification (Clauset, 2005; Schaeffer, 2005;
Chen et al., 2009). But local approaches have a lack-
ing quality compared to approaches that cluster entire
networks and they are overly dependant on a well cho-
sen start node (Bagrow, 2008).
In this paper we focus on improving local com-
munity identification algorithms in order to increase
their overall quality and reduce the dependency on the
start node. First we discuss local community struc-
ture, then we propose an improvement to local algo-
rithms and finally we present benchmark results and
discussion thereof.
400
Koopmans F. and van der Weide T..
BROADER PERCEPTION FOR LOCAL COMMUNITY IDENTIFICATION.
DOI: 10.5220/0003069204000403
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 400-403
ISBN: 978-989-8425-28-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

2 LOCAL COMMUNITY
IDENTIFICATION
A local community is considered from the perspec-
tive of a start node from which that community can
be generated. As a consequence, each node in the lo-
cal community has a special relation with this start
node and the local community as a whole is a reg-
ular community in the network. Local communities
are a soft clustering, where each node can be a mem-
ber of multiple communities, of a part of a network
thus overlap may occur. The ideal local community
for some start node v would be the community with
the highest quality that contains v. Let the quality of a
community C ⊆ N be quantified by community quality
measure µ(C).
A community is denoted as the set of nodes it con-
sist of. We define the universe of a community C, de-
noted as U(C), as all nodes that are outside of C and
adjacent to any node within C.
U(C) =
v ∈ N −C
∃
u∈C
[u → v]
(1)
The boundary of C, denoted as B(C), consists of
the nodes within the local community that have a re-
lation with nodes outside that community.
B(C) =
u ∈ C
∃
v∈U(C)
[u → v]
(2)
We introduce node relation ϕ(C, u, v) to indicate
that in community C node u is related to node v. This
relation is expressed by a path from u to v within that
community:
ϕ(C, u, v) ≡ u → v ∨ ∃
x∈C
[u → x ∧ ϕ(C, x, v)] (3)
where u → v denotes that there is an edge from u to v.
A local community C from the perspective of start
node v is a proper community, denoted as Φ(C, v), if
all its nodes are related to the start node:
Φ(C, v) = v ∈ C ∧ ∀
x∈C−v
[ϕ(C, v, x)] (4)
In that case, we refer to v as a proper generator of C.
A local community C may have different generators.
Furthermore, a node may be the generator of different
communities.
We will assume that the communities that can be
properly generated from the same start node can be
ordered hierarchically according to the subset rela-
tion:
Φ(C
1
, v) ∧ Φ(C
2
, v) =⇒ (5)
∃
C
[Φ(C, v) ∧C ⊆ C
1
∧C ⊆ C
2
]
We will call C a root community from node v, de-
noted as Φ
+
(C, v), if C is a minimal community that
can be properly generated from v:
Φ
+
(C, v) ≡ ∀
X
[Φ(X, v) ∧ X ⊆ C =⇒ X = C] (6)
Lemma 1. Let Φ
+
(C, v), then C =
T
X
Φ(X, v)
.
Note that Φ is not related to community quality.
The ideal local community for some start node v will
be a local community properly generated by v with
a maximal µ-score. We introduce argmax
x∈X
f (x) to
indicate that x ∈ X yields a result for f (x) that is not
surpassed by any value in X:
argmax
x∈X
f (x) =
x ∈ X
∀
y∈X
[ f (y) ≤ f (x)]
(7)
Let the set of communities where v is a proper
generator, denoted as ζ(v), be defined as:
ζ(v) =
C ⊆ N
Φ(C, v)
(8)
then the set of ideal communities for start node v, de-
noted as I(v), is defined as:
I(v) = argmax
C∈ζ(v)
µ(C) (9)
where multiple ideal local communities imply there
are different local community compositions for start
node v that yield the same µ-score, which is the max-
imum.
The computation of these ideal communities is not
feasible in practise because of the time complexity of
this measure. While we cannot use this concept in
practise it does provide insight in the desired result
from a local algorithm. It sets a goal, find the best
local community around a given start node.
3 BROADENING THE LOCAL
SCOPE
A strong advantage of global community identifica-
tion algorithms over their local counterparts is knowl-
edge of the entire network. For a local algorithm there
is no way of telling what lies beyond the universe of
the community it is building. There may be knowl-
edge about general network characteristics, but node
specific information is not available. This shortsight-
edness has a negative impact on the quality of the
resulting local community because local algorithms
tend to halt at every sign of community quality de-
cline, they cannot see possible improvement beyond.
A related and common problem for local algo-
rithms is their dependence on a well chosen start
node. Direct neighbors of a start node may not seem
like good building blocks for a community. A com-
monly applied band-aid solution to the start node de-
pendency is to make the local algorithm ignore its
stopping criterion until hitting a predetermined size or
quality to discourage preemptive stopping. But this
method relies on a preset threshold and thus priori
knowledge of the expected community size and struc-
ture. Also, after this preset threshold has been reached
BROADER PERCEPTION FOR LOCAL COMMUNITY IDENTIFICATION
401

the algorithm will still fail to see beyond minor barri-
ers.
We suggest the improvement of local community
identification algorithms in general by adding more
contextual information to their selection criteria. By
making a local algorithm look ahead further than one
edge from the community we decrease the shortsight-
edness of this approach and allow for a more informed
and balanced judgement on community membership,
at the cost of higher computational and situational
crawling complexity. This improvement can be ap-
plied to any local algorithm.
We propose the following example application
where we extend the algorithm its network knowledge
by offering nodes one step beyond the universe. Be-
sides the universe node itself, we also investigate the
addition of that a node together with any combination
of its neighbors. This will provide insight into pos-
sible local community structure, and quality, that lies
beyond the community universe. The set of possible
addition sets for community C at distance 2, denoted
as A(C), is defined as follows:
A(C) =
[
u∈U(C)
X ∪{u}
X ∈ ℘(b(u))
(10)
where b(u) =
v
u → v
is the set of nodes that can
be reached from u in one step. Then we are interested
in:
argmax
C
0
∈A(C)
µ(C ∪C
0
) (11)
Note that the computational complexity will in-
crease rapidly as the lookahead distance k is in-
creased, especially in dense networks. Further re-
search should consider different distances for the
lookahead approach, consider the quality and com-
putational complexity tradeoff and determine an opti-
mum (if any).
4 VALIDATION
Our improvement to local community identification
algorithms as proposed in section three is validated
by a series of tests on synthetic networks. Since we
aim to verify the improvement of local identification
algorithms in the area where these often struggle we
will generate networks with a low average degree (4,
5 and 8). This will result in networks that contain a
lot of potentially troublesome start nodes. We will
run four tests on every node in the network, varying
the algorithm (regular or improved) and the commu-
nity measure. We measure community quality by the
widely known local modularity (Clauset, 2005) and
relative density (Schaeffer, 2005; Lancichinetti et al.,
2009) definitions.
For our test we generate an undirected network
according to the Barabsi–Albert model (Albert and
Barabasi, 2002) and rewire it to create a flat commu-
nity structure as proposed by Bagrow (Bagrow, 2008).
The rewiring is done by creating k sets of nodes (rep-
resenting the communities) in the network and then
rewiring inter-community edges to intra-community
edges while preserving the degree distribution. Our
benchmark networks contain 128 nodes equally di-
vided amongst 4 communities.
The quality of a community identification algo-
rithm is evaluated by quantifying the similarity be-
tween the algorithm output and the synthetic commu-
nity structure. We will adopt the Jaccard Similarity
Coefficient (JSC) which is defined as the commonal-
ity of both sets divided by their generality:
JSC(X,Y ) =
|X ∩Y |
|X ∪Y |
(12)
4.1 Results
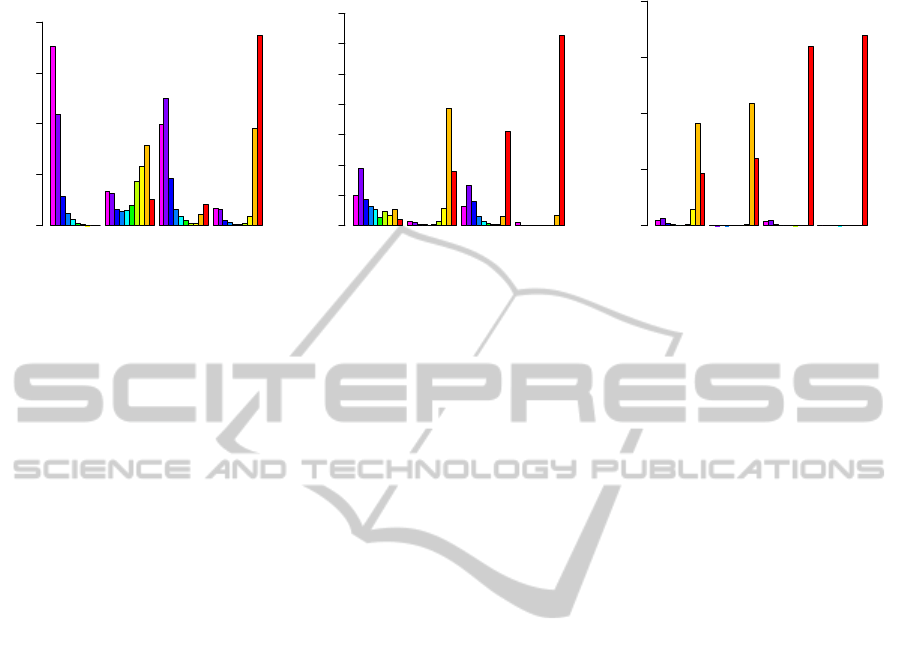
Running these tests on 50 generated networks yields
the plot of the JSC score frequency shown in Figure
1. In the networks with an average degree of 4 and
5 we observe a significant increase in high similar-
ity and decrease of outliers for both quality measures
when our algorithm improvement is applied. There
is a relatively low gain for the more dense networks
with average degree 8. The plots also show that the re-
sult, while strongly improved, is not perfect yet. We
observe a couple of reasons why even the improved
algorithm is struggling for some start nodes.
First of all, when the boundaries of two communi-
ties are not very sharp and the start node is a bound-
ary node (as defined by the synthetic graph structure)
the algorithm may start of in the wrong direction and
identify the wrong community. Suppose we start with
node v that is a member of community C according
to the synthetic structure. If the algorithm identifies
C
0
∪ v where C
0
is another community defined by the
synthetic structure, then the result of the algorithm
may be a quite strong community. But the similar-
ity measure will yield a bad result because there is
very little overlap between the reference community
and the found community.
Also, the local algorithm may find a strong com-
munity that is a subset of the community it is sup-
posed to find. The gap between the found commu-
nity and agglomerating until the algorithm identifies
a larger and stronger community may be too large for
the lookahead algorithm to recognize. There lies a
tradeoff between the time complexity of the looka-
head algorithm and the effectiveness of identifying
improvement beyond the universe candidates.
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
402
LM LM2 RD RD2
avgdeg 4
Jaccard Similarity Coefficient
frequency
0 1000 2000 3000 4000
LM LM2 RD RD2
avgdeg 5
Jaccard Similarity Coefficient
frequency
0 1000 3000 5000 7000
LM LM2 RD RD2
avgdeg 8
Jaccard Similarity Coefficient
frequency
0 2000 4000 6000 8000
Figure 1: This barplot illustrates the amount of times a test resulted in a score in the range of [0..1] for all four tests. A higher
frequency of high scores indicates a better result. LM2 and RD2 show the results when the improved algorithm is applied and
the community quality is measured by Local Modularity and Relative Density respectively.
Finally, the use of the synthetic network structure
while measuring quality is not ideal. When the goal
of a local algorithm is to identify the strongest com-
munity around a start node (as is the case in this pa-
per) that synthetic reference community may not be
the strongest community thus we may not compare
the algorithm output with the ideal community.
5 CONCLUSIONS
Local community identification is particularly useful
in large networks where only a small part of the net-
work is of interest. However, the quality of local
identification algorithms is lacking when compared to
their global counterparts. In this paper we suggest the
addition of contextual information beyond the direct
neighbors of a local community when evaluating lo-
cal community candidates. By decreasing the gap be-
tween relevant network knowledge of global and local
methods we improve the quality of local community
identification algorithms in general.
Our experiments on synthetic networks have
shown promising results. Extending generic local
community identification algorithms such that they
consider nodes one step beyond their universe will
lead to a significant increase in quality and decrease
on start node dependency.
After deriving this approach from theory and
showing a proof of concept in this paper we are in-
terested in further research on several aspects. Firstly,
as suggested in section three, one should consider sev-
eral distances k where k > 1. Secondly, an analysis of
the computational complexity of this approach is re-
quired (while also considering varying network den-
sities). This should lead to an improved experiment
using both synthetic and real world datasets to deter-
mine the appropriate tradeoff between computational
complexity and quality.
REFERENCES
Albert, R. and Barabasi, A.-L. (2002). Statistical mechanics
of complex networks. Reviews of Modern Physics,
74:47–97.
Bagrow, J. (2008). Evaluating local community methods in
networks. J. Stat. Mech., page P05001.
Chen, J., Zaane, O., and Goebel, R. (2009). Local com-
munity identification in social networks. ASONAM,
pages 237–242.
Clauset, A. (2005). Finding local community structure in
networks. Phys. Rev. E, 72:026132.
Danon, L., Duch, J., Diaz-Guilera, A., and Arenas, A.
(2005). Comparing community structure identifica-
tion. J. Stat. Mech., page P09008.
Lancichinetti, A. and Fortunato, S. (2009). Community de-
tection algorithms: a comparative analysis. Phys. Rev.
E, 80:056117.
Lancichinetti, A., Fortunato, S., and Kertesz, J. (2009).
Detecting the overlapping and hierarchical commu-
nity structure of complex networks. New Journal of
Physics, 11:033015.
Newman, M. (2003). The structure and function of complex
networks. SIAM Review, 45:167–256.
Palla, G., Barabasi, A.-L., and Vicsek, T. (2007). Quantify-
ing social group evolution. Nature, 446:664–667.
Schaeffer, S. (2005). Stochastic local clustering for mas-
sive graphs. Lecture Notes in Artificial Intelligence,
3518:354360.
Strogatz, S. (2001). Exploring complex networks. Nature,
410:268–276.
BROADER PERCEPTION FOR LOCAL COMMUNITY IDENTIFICATION
403
