
SEMANTIC SEARCH FOR ENTERPRISES
COMPETENCIES MANAGEMENT
Anna Formica, Michele Missikoff, Elaheh Pourabbas and Francesco Taglino
Istituto di Analisi dei Sistemi ed Informatica “A. Ruberti”, Viale Manzoni 30, I-00185, Rome, Italy
Keywords: Similarity Reasoning, Reference Ontology, Information content, Digital Resources.
Abstract: This paper presents a method for semantic search and retrieval in the context of networked enterprises that
share services, competencies (knowledge), and a reference ontology (RO). The RO models the universe of
domain competencies and is used to build the company profiles starting from their key documents. The
search engine is used to identify the competencies needed in a given project. A semantic search engine is
capable of representing a user request in terms of the RO concepts and identifying the collection of services
or skills (offered by a specific enterprise) that match at best the user request. The proposed semantic search
method, referred to as SemSim, is based on concept similarity, derived from the well-known notion of
information content. Concepts in the RO are weighted according to a frequency approach. Such weights are
used, in our proposal, to derive the pair-wise concept similarity, and an optimized method for computing the
similarity of conceptual structures. Finally, we report an experimental assessment where we show that our
SemSim method performs better than some of the most representative similarity search methods defined in
the literature.
1 INTRODUCTION
In this paper, we propose an ontology-based search
method for large document bases. In particular, we
developed this approach in the context of an
enterprise cluster (e.g., Digital Business Ecosystem,
Collaborative Network), where enterprises share
services and competencies. In this context, our aim
is to support competencies and skills management,
in order to improve cooperation among the
enterprises and their capability to quickly respond to
market opportunities. We assume that the cluster has
a collection of digital documents obtained by the
union of all the documents made available by each
enterprise. We will refer to this collection as the
Universe of Digital Resources (UDR). Documents in
the UDR are intended to describe the competencies
of the enterprises in the cluster. In this paper, we
refer to a cluster of enterprises in the tourism domain
(i.e., hotels). Thus, the UDR is composed by the
leaflets of the hotels, and their competencies
represent the services they offer (e.g., recreational
activities, variety of meals). When a new business
opportunity arises, for instance the request of
hosting a group of people in a hotel with certain
facilities, there is the need to find the hotel that at
best fulfills the request. To this end, the system
performs a search over the whole UDR identifying
the most suited enterprises on the basis of the
literature they produced (this is naturally the first
step, then other criteria will come into play).
To this end, we propose a semantic search method
referred to as SemSim that uses an ontology as its
foundation. Ontology-based search methods
represent a promising research direction towards a
new generation of semantic search engines, capable
of overcoming the limitations of current keyword-
based technology. Semantic search is an active
research area and several proposals exist in the
literature that are based on a given reference
ontology (RO) and some forms of mapping, often
referred to as semantic annotations, among the RO
and the documents to be searched. Often, the user
request, expressible in natural language, is
associated with a semantic annotation (composed by
concepts from the RO) that will be matched with the
semantic annotations of the documents. The output
will be a list of resources ranked by decreasing
similarity to the user request. We refer to this
process as semantic similarity reasoning.
There are several proposals in the literature on
ontology matchmaking and semantic similarity
reasoning. Some of them adopt techniques based on
183
Formica A., Missikoff M., Pourabbas E. and Taglino F..
SEMANTIC SEARCH FOR ENTERPRISES COMPETENCIES MANAGEMENT .
DOI: 10.5220/0003069801830192
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 183-192
ISBN: 978-989-8425-29-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

the information content of the concepts in the RO.
The information content of a concept c is computed
according to the well-known expression: -log(p(c)),
where p(c) is the probability that a document deals
with the concept c. Here, a crucial problem is how to
obtain the value of p(c). The large majority of
proposals (see the next section on related work) use
the probabilities derived from WordNet frequencies
(WordNet, 2010). However, as shown in the related
work section such measures are not very accurate
and, often are not available for all possible concepts.
In a previous work (Formica et al., 2008), we
adopted a probabilistic approach proposing an
alternative to the measures provided by WordNet. In
this work, we address a frequency approach: since
we operate within a cluster of enterprises, and
therefore in a closed UDR, we have a ―controlled‖
situation where it is possible to replace the estimate
of a probability with the factual measure of the
relative frequency of the concepts in the UDR. The
relative frequency of a concept is obtained from the
number of resources containing the concept over the
total number of digital resources in the UDR. In
particular, in this paper we present an experimental
result showing that the frequency approach has a
higher correlation with human judgment than the
probabilistic approach introduced in (Formica et al.,
2008), and some representative methods defined in
the literature.
The SemSim method is articulated according to
two phases: a preparatory and an execution phase.
The preparatory phase is necessary to set up the
semantic infrastructure by: (i) developing a RO, (ii)
providing a semantic annotation to each document in
the UDR, (iii) analyzing the documents in the UDR
to determine the relative frequency of the concepts
in the RO. Such a phase is time consuming and
costly, but it takes place only once at the constitution
of the cluster of enterprises, and then there are only
periodical updates. The execution phase, performed
on-the-fly at request time, is articulated according to
the following steps: (a) the semantic annotation of
the user request; (b) the matchmaking between the
semantic annotation of the user request and the
semantic annotation of each document in the UDR,
yielding a semantic similarity measure; (c) the
ranking of the documents by descending similarity
degrees.
The rest of the paper is structured as follows. In
the next section the related work is given. In Section
3, some basic notions used in SemSim are recalled.
In Section 4, the probabilistic approach is recalled,
and the frequency approach is introduced, and the
weighted reference ontology of our running example
is presented. In Section 5, the SemSim method for
evaluating semantic similarity is given. In Section 6,
an assessment of the Semsim method is presented.
Finally, Section 7 concludes the paper.
2 RELATED WORK
In the vast literature available (see for instance,
(Alani and Brewster, 2005), (Euzenat and Shvaiko,
2007), (Madhavan and Halevy, 2003), (Maguitman,
et al., 2005)), we will restrict our focus on the
proposals tightly related to our approach. We wish to
emphasize that the focus of our work is both on the
assignment of weights to the concepts of a reference
ontology, and the method to compute the similarity
between concept vectors. The following subsections
concern these two aspects.
2.1 The Weight Assignment
In the large majority of papers proposed in the
literature (Euzenat and Shvaiko, 2007), (Maguitman,
et al., 2005), assignment of weights to the concepts
of a reference ontology (or a taxonomy) is
performed by using WordNet (WordNet, 2010), see
for instance (Kim and Candan, 2006), (Li et al.,
2003), and also (Resnik, 1995), (Lin, 1998) which
inspired our method. WordNet (a lexical ontology
for the English language) provides, for a given
concept (noun), the natural language definition,
hypernyms, hyponyms, synonyms, etc, and also a
measure of the frequency of the concept. The latter
is obtained by using noun frequencies from the
Brown Corpus of American English (Francis and
Kucera, 1979). Then, the SemCor project (Fellbaum
et al., 1997) made a step forward by linking
subsections of Brown Corpus to senses in the
WordNet lexicon (with a total of 88,312 observed
nouns). We did not adopt the WordNet frequencies
for two reasons. Firstly, we deal with specialised
domains (e.g., systems engineering, tourism, etc.),
requiring specialised domain ontologies. WordNet is
a generic lexical ontology (i.e., not focused on a
specific domain) that contains only simple terms. In
fact, multi-word terms are not reported (e.g., terms
such as ―seaside cottage‖ or ―farm house‖ are not
defined in WordNet). Secondly, there are concepts
in WordNet for which the frequency is not given
(e.g., ―accommodation‖) or is irrelevant, as in the
case of ―meal‖ (the frequency is 20).
Concerning weight assignment, in (Fang et al.,
2005) the proposal makes a joint use of an ontology
and a typical Natural Language Processing method,
based on term frequency and inverse document
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
184

frequency (tf-idf). Therefore, in weighting the
similarity between terms and elements of the
ontology, the authors propose a rigid approach based
on five relevance levels corresponding to five
constants: direct(1.0), strong(0.7), normal(0.4),
weak(0.2), irrelevant(0.0). In our semantics-based
approach, the weights and the similarity between
concepts may take any value between 0 and 1.
The work presented in (Kim and Candan, 2006)
shares some analogies with our approach with regard
to the need of computing weights without relying on
large text corpora. Therefore, they propose a
method, referred to as CP/CV, such that each node
in the taxonomy is associated with a concept vector,
built on the basis of the topology of the ontology and
the position of concepts therein. Then, the similarity
of concepts is evaluated according to the cosine
similarity of the related concept vectors. Conversely,
in our work the similarity of concepts (consim) is
conceived to determine the similarity of two concept
vectors (semsim).
As already mentioned in the Introduction, with
respect to the probabilistic approach presented in
(Formica et al., 2008) in this paper we address a
frequency approach which shows a higher
correlation with human judgment (see Section 6).
2.2 The Method
Once weights have been assigned to the concepts of
the RO, our work proposes a two stages method,
firstly computing the pair-wise concept similarity
(consim), and then deriving the similarity between
vectors of concepts (semsim). As anticipated, pair-
wise concept similarity is performed according to
the information content approach, originally
proposed by Resnik (Resnik, 1995) and successively
refined by Lin (Lin, 1998). The Lin’s approach
shows a higher correlation with human judgement
than other methods, such as the edge-counting
approach (Rada et al., 1989) and Wu-Palmer (Wu
and Palmer, 1994). The second stage consists in
computing vector similarity. To this end we adopted
a solution inspired by the maximum weighted
matching problem in bipartite graphs. Below some
proposals concerning methods for evaluating the
similarity between sets (or vectors) of concepts are
recalled.
In the literature the Dice and Jaccard (Maarek et
al., 1991) methods are often adopted in order to
compare vectors of concepts. However, in both
above mentioned methods the matchmaking of two
concept vectors is based on their intersection,
without considering the position of the concepts in
the ontology. Our proposal is based on a more
refined semantic matchmaking, since the match of
two concepts is performed according to their shared
information content, and the vector similarity is
based on the optimal concept coupling.
In (Cordì et al., 2005) two algorithms for
computing the semantic distance/similarity between
sets of concepts belonging to the same ontology are
introduced. They are based on an extension of the
Dijkstra algorithm (Dijkstra, 1959) to search for the
shortest path in a graph. With respect to our
approach, in the mentioned paper the similarity is
based on the distance between concepts rather than
the information content of each concept.
Furthermore, the similarity between sets of concepts
is computed by considering the similarity among
each concept from a set and all the concepts from
the other set. The similarity between adjacent
concepts is supposed to be decided at design-time by
the ontology developer and consequently introduces
a certain degree of rigidity and bias on the results.
In (Li et al., 2003), a similarity measure between
words is defined, where each word is associated with
a concept in a given ISA hierarchy. The proposed
measure essentially combines path length between
words, depth of word subsumers in the hierarchy,
and local semantic density of the words. Finally, the
authors evaluate their method using WordNet that,
as anticipated, is not appropriated for specialized
applications.
Note that the use of ontologies for semantic
search has been extensively investigated in the
biomedical field (see for instance
www.geneontology.org).
3 BASIC NOTIONS
In this section, we recall some of the definitions
introduced in (Formica et al., 2008) that will be used
in this paper.
The Universe of Digital Resources (UDR) is the
totality of the digital resources that are semantically
annotated with a reference ontology (an Ontology is
a formal, explicit specification of a shared
conceptualization (Gruber, 1993)). In our work we
address a simplified notion of ontology, Ont,
consisting in a set of concepts organized according
to a specialization hierarchy. In particular, Ont is a
taxonomy defined by the pair:
Ont = <C, H>
SEMANTIC SEARCH FOR ENTERPRISES COMPETENCIES MANAGEMENT
185

where C is a set of concepts and H is the set of pairs
of concepts of C that are in subsumption (subs)
relation:
H = {(c
i
,c
j
) CC | subs(c
i
,c
j
)}
Given two concepts c
i
, c
j
C, the least upper bound
of c
i
, c
j
, lub(c
i
,c
j
), is always uniquely defined in C
(we assume a lattice structure for the hierarchy). It
represents the least abstract concept of the ontology
that subsumes both c
i
and c
j
.
Consider an ontology Ont = <C, H>. A request
feature vector (request vector for short) rv is defined
by a set of ontology concepts:
rv = (c
1
,...,c
n
) where c
i
C
Analogously, given a digital resource dr
i
UDR, an
ontology feature vector (OFV) ofv
i
associated with
dr
i
is a set of ontology concepts describing the
resource:
ofv
i
= (c
i,1
,...,c
i,m
) where c
i,j
C, j = 1,...,m
A Weighted Reference Ontology (WRO) is a pair:
WRO = <Ont, w>
where w is a function defined over C, such that
given a concept c C, w(c) is a rational number in
the interval [0,...,1]. In the following we will use w
p
to denote the weight associated with c in the
probability approach and w
f
to denote the relative
frequency of the same concept. We will see, in the
next sections, that the definition of WRO allows us
to define two notions of similarity: the pair-wise
concept similarity (consim) and the feature vectors
similarity (semsim).
A request vector denotes all the digital resources
in UDR whose OFVs contain at least one feature in
rv or one feature that is similar to (at least) one
feature in rv, up to a threshold (consim similarity).
For instance, consider a fragment of the example
drawn from the tourism domain presented in
(Formica et al., 2008). Note that, the complete
example will be given in Section 4. In the example
we consider a dozen of hotels, H1,...,H12, having
their leaflets annotated by using a common WRO.
Below, some of the OFVs are given to better clarify
some definitions underlying the proposed search
method. They are:
ofv
1
= (InternationalHotel, Golf, InternationalMeal, Theatre)
ofv
6
= (CountryResort, LightMeal, ClassicalMusic)
ofv
11
= (SeasideCottage, VegetarianMeal, Tennis)
ofv
12
= (SeasideCottage, VegetarianMeal)
Consider now a user request:
"I would like to stay in a seaside hotel, where I can
have a recreational activity"
that can be formulated in terms of a request feature
vector as follows:
rv = (SeasideCottage, RecreationalActivity)
The set denoted by rv includes the resources H11
and H12 because both are annotated by the feature
SeasideCottage. Note that there are no resources
whose ofv explicitly contains RecreationalActivity.
However, Theatre, ClassicalMusic, and Tennis can
be considered recreational activities. Therefore, our
approach also returns all the resources annotated by
at least one feature that is similar to
RecreationalActivity, up to a given threshold. This
kind of similarity is evaluated according to consim
that allows us to compute, for instance, the similarity
degree between RecreationalActivity and Theatre
according to the information content approach.
The SemSim methodallows us to evaluate the
similarity between OFVs according to the maximum
weighted matching problem that will be recalled in
subsection 5.2. Once SemSim between the rv and
each OFV has been computed the Ranked Solution
Vector (RSV) associated with rv, RSV(rv), can be
defined as follows:
RSV(rv) = {(dr
j
, semsim) | dr
j
UDR and
semsim(rv,ofv
j
) > h}
where semsim(rv,ofv
j
) is the semantic similarity
between the feature vector ofv
j
associated with dr
j
and rv, and h is a given threshold.
4 FREQUENCY-BASED WEIGHT
ASSIGNMENT
As seen in Section 3, the construction of the OFVs
requires a RO, while the computation of the semsim
function needs a WRO, that is obtained by
associating a weight with each concept in the
reference ontology.
In this work, the probabilistic approach presented
in (Formica et al., 2008) is recalled and successively
the frequency approach is presented, which is the
focus of this paper. In Figure 1, an ISA hierarchy,
representing our WRO, is defined where the weights
related to the above mentioned approaches have
been computed and are labelled as w
p
and w
f
,
respectively.
The approach presented in the mentioned paper
is based on a simple probabilistic distribution along
the ISA hierarchy. The root of the hierarchy is
referred to as Thing, and its weight, denoted by
w
p
(Thing), is equal to 1. Then, for any other concept
c, say c’ the father of c, w
p
(c) is equal to the
probability of c’, divided by number of the children
of c’:
w
p
(c) = w
p
(c’) / | children(c’) |
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
186

Figure 1: Concept weights as uniform probabilistic distribution and relative frequencies.
For instance, let us consider the concept Open-
air Activity, where w
p
(Open-air Activity) = 0.17,
since w
p
(RecreationalActivity)= 0.33 and
Recreational-Activity has two subconcepts.
In our proposal, the frequency approach, the
weight assignment is based on the computation of
the relative frequency w
f
of each concept c:
w
f
(c) = | { ofv : c
ofv } | / | UDR |
This approach needs that the OFVs associated with
the resources in UDR have been already defined. In
our example, we assume to have a dozen of hotels
leaflets annotated by means of OFVs, as shown in
Table 1.
Note that the construction of the OFVs is a process
which can be supported by the well-known term
extraction techniques (see for instance (Velardi et
al., 2007)), which goes beyond the scope of this
paper.
For instance, let us consider the feature Biking.
This feature appears in ofv
2
, ofv
9
, and ofv
10
(see
Table 1). Thus, the relative frequency of this feature
over the whole resources (hotels) is w
f
(Biking)=3/12
(see Figure 1). Similarly, Golf is a feature belonging
to ofv
1
, and ofv
9
and Tennis appears in ofv
3
, and
ofv
11
. Therefore w
f
(Golf)=2/12, and
w
f
(Tennis)=2/12. To assign a weight to the more
abstract concepts we consider the essence of the ISA
relationship. For instance, Golf is an Open-air
Activity and Tennis too. Therefore, even if Open-air
Activity does not explicitly appear in digital
resources of Table 1, its frequency, w
f
(Open-air
Activity)=6/12, is calculated as distinct count of
OFVs, in which the concepts Biking, Golf, Tennis
and Open-air Activity appear as features in the
ontology. They are: ofv
1
, ofv
2
, ofv
3
, ofv
9
, ofv
10
, ofv
11
.
Table 1: OFV-based annotation of Digital Resources.
ofv
1
= (InternationalHotel, Golf, InternationalMeal, Theatre)
ofv
2
= (Pension, FrenchMeal, Biking, Reading)
ofv
3
= (CountryResort, MediterraneanMeal, Tennis)
ofv
4
= (CozyAccommodation, ClassicalMusic, InternationalMeal)
ofv
5
= (InternationalHotel, ThaiMeal, IndianMeal, ClassicalMusic)
ofv
6
= (CountryResort, LightMeal, ClassicalMusic)
ofv
7
= (SeasideCottage, EthnicMeal, CulturalActivity)
ofv
8
= (CountryResort, VegetarianMeal, CulturalActivity)
ofv
9
= (SeasideCottage, MediterraneanMeal, Golf, Biking)
ofv
10
= (RegularAccommodation, RegularMeal, Biking)
ofv
11
= (SeasideCottage, VegetarianMeal, Tennis)
ofv
12
= (SeasideCottage, VegetarianMeal)
Overall, in the probabilistic distribution approach
the weights can be assigned in a top-down way,
starting from the root of the ISA hierarchy to the
leaves. Conversely, the frequency approach follows
a bottom-up assignment, which starts from the
leaves of the hierarchy.
SEMANTIC SEARCH FOR ENTERPRISES COMPETENCIES MANAGEMENT
187

5 THE SEMSIM METHOD
In order to compare the probabilistic and frequency
approaches, let us consider the user request defined
in (Formica et al., 2008) that is recalled below:
"I would like to stay in a seaside hotel, where I can
have vegetarian food, play tennis, and attend
sessions of classical music in the evening".
It can be formulated according to the request feature
vector notation as follows:
rv = (SeasideCottage, VegetarianMeal, Tennis,
ClassicalMusic)
Once the rv has been specified, the Semsim method
is able to evaluate the semantic similarity (semsim)
among the rv and each available OFV. As already
mentioned, in order to compute the semsim between
feature vectors, it is necessary first to compute the
similarity (consim) between pairs of concepts.
5.1 Computing Concept Similarity:
Consim
The consim method relies on the information content
approach defined by Lin (Lin, 1998). According to
the standard argumentation of information theory,
the information content of a concept c is defined as -
log w(c). Therefore, as the weight of a concept
increases the informativeness decreases, hence, the
more abstract a concept the lower its information
content. Given two concepts c
i
and c
j
, their
similarity, consim(c
i
,c
j
), is defined as the maximum
information content shared by the concepts divided
by the sum of the information content of the two
concepts. Note that, since we assume that the
ontology is a tree, the least upper bound of c
i
and c
j
,
lub(c
i
,c
j
), is always defined and provides the
maximum information content shared by the
concepts in the taxonomy. Formally, we have:
consim(c
i
,c
j
)=
2 log w(lub(c
i
,c
j
)) / (log w(c
i
)+log w(c
j
))
which holds for both the probabilistic and frequency
approaches. For instance, consider the pair of
concepts ClassicalMusic and Reading of the WRO
shown in Figure 1, the consim is defined as follows:
consim(ClassicalMusic, Reading) =
2 log w
f
(CulturalActivity) /
(log w
f
(ClassicalMusic)+log w
f
(Reading))=0.28
Since CulturalActivity is the lub of ClassicalMusic
and Reading, it therefore provides the maximum
information content shared by the comparing
concepts.
5.2 Computing Semantic Similarity:
Semsim
The SemSim method allows us to derive the
semantic similarity of two vectors, rv and ofv,
semsim(rv,ofv), by using the consim function. In
principle, we start from the Cartesian product of the
mentioned vectors. For each pair we can derive the
similarity consim, as seen in the previous section.
However, we do not need to consider all possible
pairs, since in many cases the check is meaningless
(e.g., contrasting a vegetarian meal with a classical
music concert). Hence, we aim at restricting our
analysis considering only the pairs that exhibit a
higher affinity. Furthermore, we adopted the
exclusive match philosophy (sometimes named
stable marriage problem) where once a pair of
concepts has been successfully matched, they do not
participate in any other pair. For instance, assuming
rv and ofv represent a set of boys and a set of girls
respectively, we analyze all possible sets of
marriages, when polygamy is not allowed. Our
solution, for the computation of the semantic
similarity makes use of the Hungarian algorithm for
solving the maximum weighted matching problem in
bipartite graphs (Formica and Missikoff, 2002),
(Formica, 2009) which runs in polynomial time.
Essentially, the method aims to identify the sets of
pairs of concepts of the two vectors that maximize
the sum of consim:
semsim(rv,ofv) = max(
consim(c
i
,c
j
)) / max(n,m)
where: i = 1..n, j = 1..m, n = |rv|, m = |ofv|, c
i
rv,
and c
j
ofv.
For instance, according to the frequency
approach (see Figure 1), in the case of rv and ofv
9
of
our running example, the following set of pairs of
concepts (enclosed in brackets) has the maximum
consim sum:
consim(SeasideCottage, SeasideCottage)= 1.00
consim(VegetarianMeal, MediterraneanMeal)= 0.44
consim(Tennis, Golf)=0.39
consim(ClassicalMusic, Biking)=0.06
Therefore:
semsim(rv, ofv
9
) =
(1.00 + 0.44 + 0.39 + 0.06) / 4 = 0.47
where the sum of consim has been normalized
according to the maximum cardinality of the
contrasted vectors (in this case, it is 4 both).
6 SEMSIM EVALUATION
The evaluation of the SemSim method is based on
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
188

Table 2: Results of the comparison among human judgment, SemSim and selected similarity methods.
Feature
Vectors
HJ
semsim-f
semsim-p
Dice
Jaccard
Salton’s
Cosine
Weighted
Sum
ofv
1
0.60
0.17
0.49
0.00
0.00
0.00
0.00
ofv
2
0.60
0.18
0.49
0.00
0.00
0.00
0.00
ofv
3
0.67
0.44
0.63
0.29
0.17
0.08
0.29
ofv
4
0.60
0.38
0.56
0.29
0.17
0.08
0.43
ofv
5
0.59
0.25
0.43
0.25
0.14
0.06
0.25
ofv
6
0.80
0.50
0.66
0.29
0.17
0.08
0.43
ofv
7
0.60
0.39
0.55
0.29
0.17
0.08
0.43
ofv
8
0.67
0.47
0.63
0.29
0.17
0.08
0.43
ofv
9
0.67
0.48
0.69
0.25
0.14
0.06
0.25
ofv
10
0.36
0.11
0.37
0.00
0.00
0.00
0.00
ofv
11
0.82
0.75
0.75
0.86
0.75
0.25
0.86
ofv
12
0.71
0.50
0.50
0.67
0.50
0.25
0.67
Correlation
with HJ
1.00
0.85
0.82
0.70
0.67
0.66
0.72
the experiments conducted on the resources shown
in Table 1. Essentially, we first calculate the semsim
measure through the relative frequency approach
discussed in Section 5, which in the following will
be indicated as semsim-f. Then, we contrast the
results with similarity measures obtained by using
the probabilistic approach, indicated below as
semsim-p and the selected methods: Dice, Jaccard,
Salton’s Cosine (Maarek et al., 1991) and the
Weighted Sum defined in (Castano et al., 1998)
which are among the most representative in the
literature. The similarity rating measures of these
selected methods are essentially defined by the
cardinality of the common features between the
compared concepts divided by the cardinality of the
features of each concept (see (Formica et al., 2008),
for details of their formulas). The similarity
assessment is basically explored by studying the
correlation between computational similarity
methods and people’s judgment of similarity.
Accordingly, in the mentioned paper we asked to a
selected group of 20 people to evaluate the similarity
between rv and each of the resources of our running
example, which are the hotels H
i
, i = 1,...,12,
annotated with the OFVs shown in Table 1.
In Table 2, we note that the correlation of the
similarity measures computed by semsim-f with the
human judgement is higher than the correlation
achieved by semsim-p (i.e., 0.85 vs 0.82). This
correlation is higher with respect to the correlation
achieved by the selected methods with human
judgement, as well. Note that, although the average
value of semsim-p (0.56) is closer to the average
value of human judgment (HJ) (0.64) than that of
semsim-f (0.39), the correlation of semsim-f with HJ
is greater than that of semsim-p In fact, correlation
reflects the noisiness in the linear relationship
between HJ and semsim values, that essentially
means that higher scores on HJ tend to be paired
with higher scores on semsim, and analogously for
lower scores. It is important to observe that, in our
example, the values for the semsim-f are in general
minor than that of semsim-p because all the
resources are characterized by at least one kind of
(one feature that is a descendant of) accommodation
in the WRO and, analogously, one kind of meal.
Therefore in the frequency approach
w
f
(Accommodation) = w
f
(Meal) = 1, and the
similarity between descendants of Accommodation
(or Meal), for the majority of compared pairs, is null
(i.e., the maximum information content shared by
the majority of the pairs is null). In fact, since all the
hotels provide some kinds of accommodation (e.g.,
farm or seaside) and meal (e.g. vegetarian or
Mexican), the similarity among the rv and the OFVs
depends on the kind of recreational activity offered
by the hotels (e.g., tennis or theatre).
6.1 Ranking of Results
In this section, we discuss the problem of ranking
the results shown in Table 2. For this reason, we
consider Table 3, where the digital resources are
listed according to the values assigned by human
judgement and the proposed SemSim method using
both the relative frequency and uniform probabilistic
weighting approaches, i.e., semsim-f and semsim-p.
They are ordered from the highest up to the lowest
values of similarity degrees.
Let us fix for instance the threshold to 0.40,
which is shown by horizontal lines in Table 3. This
threshold will divide the digital resources into two
SEMANTIC SEARCH FOR ENTERPRISES COMPETENCIES MANAGEMENT
189

Table 3: Ranking results.
Human Judgment (HJ)
semsim-p
semsim-f
Ranked
Resources
Values
Ranked
Resources
Values
Ranked
Resources
Values
H11
0.82
H11
0.75
H11
0.75
H6
0.80
H9
0.69
H12, H6
0.50
H12
0.71
H6
0.66
H9
0.48
H3, H8, H9
0.67
H3, H8
0.63
H8
0.47
H1, H2, H4, H7
0.60
H4
0.56
H3
0.44
H5
0.59
H7
0.55
H7
0.39
H10
0.36
H12
0.50
H4
0.38
H1, H2
0.49
H5
0.25
H5
0.43
H2
0.18
H10
0.37
H1
0.17
H10
0.11
groups. The group of digital resources shown above
the horizontal line defines the Ranked Solution
Vector (RSV) of our running example.
We apply the typical evaluation measures,
namely precision and recall, to the ranked digital
resources. Precision is defined by the number of
retrieved resources that are relevant divided by the
number of retrieved resources. Recall is defined by
the number of retrieved resources that are relevant
divided by the number of relevant resources.
For instance, in Table 3, fixed the threshold to
0.4, the ranked resources above the line in the first
column (HJ) are relevant, while the resources above
the lines in the second (semsim-p) and third
(semsim-f) columns of the table are retrieved.
According to the given threshold, in the case of the
probabilistic approach, semsim-p, the precision and
recall are both equal to 1, while in the case of the
frequency approach, semsim-f, the precision is equal
to 1 and recall is equal to 0.55.
Note that in our experiment all retrieved
resources are relevant. Thus, for any fixed threshold,
precision is always equal to 1. Figure 2 illustrates
recall for different thresholds in the case of semsim-
p and semsim-f.
We note that recall of both methods is the same for
thresholds greater than or equal to 0.70. In both
cases, for thresholds varying up to 0.50, high
thresholds will result low recall. In other words, we
extract fewer resources that are relevant by
increasing the value of the threshold in the range
0.15÷0.50.
An alternative evaluation of the Ranked Solution
Vector is to select the digital resources associated
with the m highest SemSim values among n=1,…,12.
For instance, let us consider the first three highest
similarity values in Table 3. Accordingly, we extract
H6, H11, and H12 (see first column) as relevant
digital resources. The retrieved digital resources, in
the case of semsim-p are H6, H9, H11, while in the
case of semsim-f, they are H6, H9, H11, H12. In the
case of semsim-p, precision and recall are both equal
to 0.67, while in the case of semsim-f, precision is
0.75 and recall is equal to 1.
0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80
0
0.2
0.4
0.6
0.8
1
SemSim-p SemSim-f
Threshold
Recall
Figure 2: Recall by threshold.
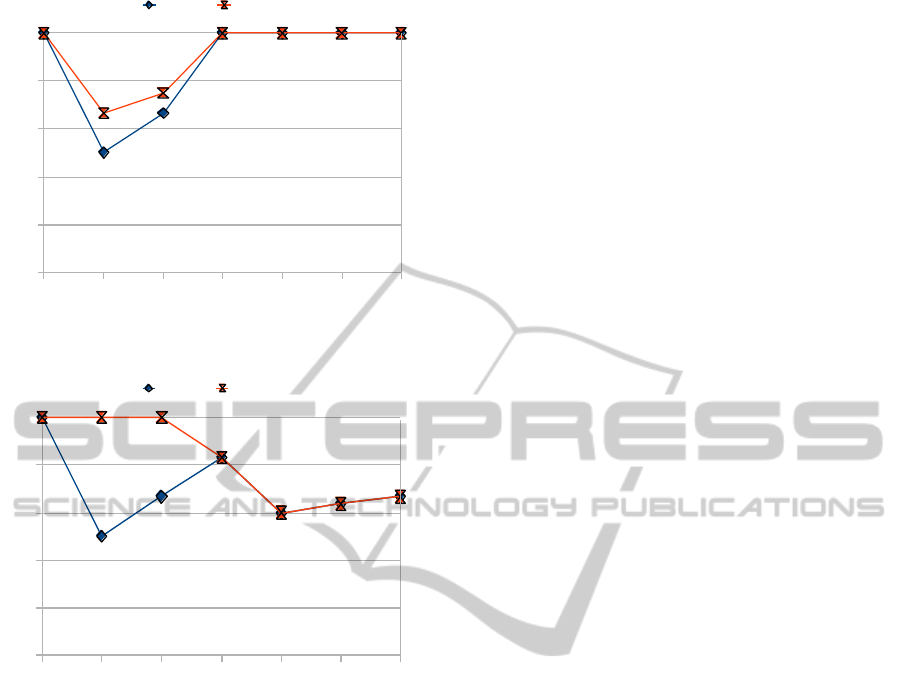
In Figure 3, and Figure 4, precision and recall for
semsim-p and semsim-f at different positions are
illustrated.
Overall, we note that semsim-f achieves higher
precision and recall with respect to semsim-p.
7 CONCLUSIONS AND FUTURE
WORKS
In this paper, we presented the key results that have
been achieved in developing the SemSim method,
aimed at semantic search and retrieval of digital
resources in the context of a cluster of enterprises.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
190
1th 2th 3th 4th 5th 6th 7th
0
0.2
0.4
0.6
0.8
1
SemSim-p SemSim-f
Position
Precision
Figure 3: Precision of semsim-p and semsim-f.
1th 2th 3th 4th 5th 6th 7th
0
0.2
0.4
0.6
0.8
1
SemSim-p SemSim-f
Position
Recall
Figure 4: Recall of semsim-p and semsim-f.
SemSim has been validated with an example in
the tourism domain, which is a preliminary
experiment showing that the proposal goes in the
right direction. In particular, our experiment shows
that the frequency approach has a higher correlation
with human judgment with respect to some of the
most popular approaches to similarity reasoning in
the literature, including a previous proposal of ours
(Formica et al., 2008). However, it is important to
note that the frequency evaluation can be costly in
some UDRs or even impossible in an open UDR.
Furthermore, the dependency of the ontology
weights on the OFVs, in the frequency approach,
requires their re-computation in the presence of any
modification to the UDR. This problem suggests us,
as a future work, to identify the conditions upon
which the updates to the set of OFVs are recognized
to be non-relevant and consequently we can assume
the weights of concepts in the ontology remain
invariant.
ACKNOWLEDGEMENTS
This work has been partly funded by the European
Commission through ICT Project COIN:
Collaboration and Interoperability for networked
enterprises (No. ICT-2008-216256). The authors wish
to acknowledge the Commission for its support. We
also wish to acknowledge our gratitude and
appreciation to all COIN project partners for their
contribution during the development of various ideas
and concepts presented in this paper.
REFERENCES
Alani, H., Brewster, C., 2005. Ontology ranking based on
the Analysis of Concept Structures. In K-CAP 2005.
Banff, Alberta, Canada.
Castano, S., De Antonellis, V., Fugini, M. G., Pernici, B.,
1998. Conceptual Schema Analysis: Techniques and
Applications. ACM Transactions on Databases
Systems, Vol. 23, No 3, pp. 286-333.
Cordì, V., Lombardi, P., Martelli, M., Mascardi, V., 2005.
An Ontology-Based Similarity between Sets of
Concepts. In proc. of WOA 2005. pp. 16-21.
Dijkstra, E. W., 1959. A note on two problems in
connexion with graphs. Numerische Mathematik, 1:
269–271.
Euzenat, J., Shvaiko, P., 2007. Ontology Matching,
Springer.
Fang, W-D., Zhang, L., Wang, Y-X., Dong, S-B., 2005.
Towards a Semantic Search Engine Based on
Ontologies. In proc. of 4
th
Int’l Conference on
Machine Learning, Guangzhou.
Fellbaum, C., Grabowski, J., Landes, S., 1997. Analysis of
a hand tagging task. In proc. of ANLP-97 Workshop on
Tagging Text with Lexical Semantics: Why, What, and
How? Washington D.C., USA.
Formica, A., 2009. Concept similarity by evaluating
Information Contents and Feature Vectors: a combined
approach. Communications of the ACM (CACM),
52(3), pp.145-149, 2009.
Formica, A., Missikoff, M., 2002. Concept Similarity in
SymOntos: an Enterprise Ontology Management Tool.
Computer Journal 45(6), 583--594 (2002).
Formica, A., Missikoff, M., Pourabbas, E., Taglino, F.,
2008. Weighted Ontology for Semantic Search. In
proc. of ODBASE 2008, Monterrey, Mexico, 11-13
November 2008.
Francis, W. N., Kucera, H., 1979. Brown Corpus Manual.
Providence, Rhode Island. Department of Linguistics,
Brown University.
Gruber, T. R., 1993. A translation approach to portable
ontologies. Knowledge Acquisition, 5(2):199-220.
Kim, J. W., Candan, K. S., 2006. CP/CV: Concept
Similarity Mining without Frequency Information
from Domain Describing Taxonomies. In proc. of
CIKM ’06.
SEMANTIC SEARCH FOR ENTERPRISES COMPETENCIES MANAGEMENT
191

Li, Y., Bandar, Z. A., McLean, D., 2003. An Approach for
Measuring Semantic Similarity between Words Using
Multiple Information Sources. IEEE Transactions on
Knowledge and Data Engineering, 15(4): 871-882.
Lin, D., 1998. An Information-Theoretic Definition of
Similarity. In proc. of 15th the International
Conference on Machine Learning. Madison,
Wisconsin, USA, Morgan Kaufmann, 296—304.
Shavlik J. W. (ed.).
Maarek, Y. S., Berry, D. M., Kaiser, G. E., 1991. An
Information Retrieval Approach For Automatically
Constructing Software Libraries. IEEE Transactions
on Software Engineering 17(8) 800—813.
Madhavan, J., Halevy, A. Y., 2003. Composing Mappings
among Data Sources. VLDB 2003: 572—583.
Maguitman, A.G., Menczer, F., Roinestad, H.,
Vespignani, A., 2005. Algorithmic Detection of
Semantic Similarity. In proc of WWW’05 Conference,
May 2005, Chiba, Japan.
Rada, L., Mili, V., Bicknell, E., Bletter, M., 1989.
Development and application of a metric on semantic
nets. IEEE Transaction on Systems, Man, and
Cybernetics, 19(1), 17--30.
Resnik, P., 1995. Using information content to evaluate
semantic similarity in a taxonomy. In proc. of IJCAI.
Sclano, F., Velardi, P., 2007. ―TermExtractor: a Web
Application to Learn the Common Terminology of
Interest Groups and Research Communities―. In proc
of 9th Conf. on Terminology and Artificial Intelligence
TIA 2007, Sophia Antinopolis.
WordNet 2010: http://wordnet.princeton.edu.
Wu, Z., Palmer, M., 1994. Verb semantics and lexicon
selection, in the 32nd Annual Meeting of the
Association for Computational Linguistics, Las
Cruces, New Mexico, pp.133-138.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
192
