A PSO-TRAINED ADAPTIVE NEURO-FUZZY INFERENCE
SYSTEM FOR FAULT CLASSIFICATION
Haris M. Khalid
1
, S. Z. Rizvi
1
, Lahouari Cheded
1
, Rajamani Doraiswami
2
and Ammar Khoukhi
1
1
King Fahd Univ. of Petroleum & Minerals, Dhahran, Saudi Arabia
2
University of New Burnswick & National Science and Engineering Research Council (NSERC), Ottawa, Canada
Keywords:
Particle swarm optimization (PSO), Hybrid neuro-fuzzy, Soft computing, ANN, ANFIS, Fault detection,
Benchmarked laboratory scale two-tank system.
Abstract:
When a fault occurs during an industrial inspection, workmen have to manually find the location and type of
the fault in order to remove it. It is often difficult to accurately find the location and type of fault. Hence,
development of an offline intelligent fault diagnosis system for process control industry is of great importance
since successful detection of fault is a precursor to fault isolation using corrective actions. This paper presents
a novel hybrid Particle Swarm Optimization (PSO) and Subtractive Clustering (SC) based Neuro-Fuzzy In-
ference System (ANFIS) designed for fault detection. The proposed model uses the PSO algorithm to find
optimal parameters for (SC) based ANFIS training. The developed PSO-SC-ANFIS scheme provides criti-
cal information about the presence or absence of a fault. The proposed scheme is evaluated on a laboratory
scale benchmark two-tank process. Leakage fault is detected and results are presented at the end of the paper
showing successful diagnosis of most incipient faults when subjected to a fresh set of data.
1 INTRODUCTION
Reliability, survivability, and classification are be-
coming major concerns in the development of most
advanced systems and processes. Successful monitor-
ing of process control equipment with the aid of intel-
ligent fault detection and classification techniques can
result in detecting equipment malfunctions and poten-
tial causes of failure in a timely fashion and while the
process is still running. This can prevent unneces-
sary and costly breakdowns and potentially fatal ca-
sualties, avoid environmental pollution and can, on
the whole, increase the lifetime of the equipment and
prevent enormous economic losses. Existing Artifi-
cial Neural Network (ANN)-based fault diagnosis ap-
proaches are effective in diagnosing and locating the
fault states of process control equipments.
In this paper, a recently developed optimiza-
tion technique, Particle Swarm Optimization (PSO)
(Kennedy, J., Eberhart, R., 2001) is used to train Sub-
tractive Clustering (SC)-based Adaptive Neuro-Fuzzy
Inference System (ANFIS). PSO has attracted much
attention among researchers and has been used to
solve complex optimization problems with wide ap-
plications in different fields (Eberhart, R., Shi, Y.,
1998). The developed PSO-SC-ANFIS is trained on
data collected from a laboratory-scale benchmark
coupled tanks. The trained ANFIS is then validated
on a fresh set of data to detect incipient leakage faults
in the tank.
The paper is organized as follows. Section 2 re-
views recent related works in the literature. The dual-
tank system used as a test-bed is described, and its
model derived in section 3. Section 4 describes in de-
tail the implementation of the proposed scheme and
discusses simulation results obtained. Finally, discus-
sions and conclusions are drawn in section 5.
2 RELATED WORKS
Artificial intelligence (AI) techniques have seen an in-
creased interest in solving fault diagnostic problems.
Application of Neural Network-based AI techniques
for fault diagnosis of systems like power transform-
ers (Ping, Y. Q., Wude, X., Zhida, L., 2005; Ping,
Q., Qun, L. M., Yun, M. X., Jun, W., 2009) and ro-
tating machines (Dou, W., Liu, Z. S., Wang, D. H.,
2007; Wei, D., Sheng, L. Z., Xiaowei, W., 2007) can
be found in the literature. An important requirement
for training an artificially intelligent system that is
required to predict the behavior of the plant is tun-
399
M. Khalid H., Z. Rizvi S., Cheded L., Doraiswami R. and Khoukhi A..
A PSO-TRAINED ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM FOR FAULT CLASSIFICATION.
DOI: 10.5220/0003072303990405
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
399-405
ISBN: 978-989-8425-32-4
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

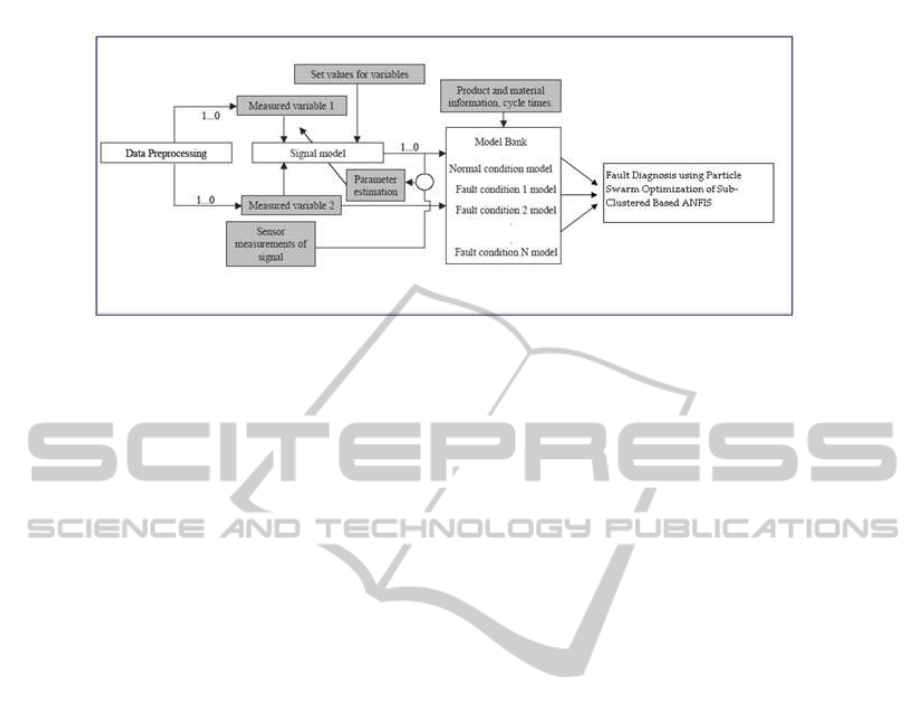
Figure 1: Proposed scheme.
ing its key parameters to optimal values during its
training. With the rapid rise of heuristic algorithms,
researchers have found more reliable means to find
optimal solutions to AI learning problems. Genetic
Algorithm (GA) (Dou, W., Liu, Z. S., Wang, D. H.,
2007; Wei, D., Sheng, L. Z., Xiaowei, W., 2007; El-
hadef, M., Ayeb, B., 2000), Particle Swarm Optimiza-
tion (PSO) (Hongxia, P., Jinying, H., Hongwei, M.,
2009), and Grid Search based methods (Duan, F., Zi-
vanovic, R., 2009) are among severalother techniques
that have seen an increased interest and use in solv-
ing AI-based fault diagnostic problems. Various tech-
niques such as ANN, Fuzzy Logic (FL) and GA are
used to develop models for FDI techniques. These
models can be trained and used to represent a wide
class of nonlinear systems with an arbitrary accuracy.
Among these techniques, ANN-based techniques are
well recognized for their ability to approximate non-
linear functions and for their learning ability (Zhang,
G. Q. P., 2000). For these reasons, they have been
used as models to generate residuals for fault detec-
tion purposes (Wang, Y., Chan C. W., Cheung, K. C.,
2001). However, it is desirable that a fault diagnos-
tic system should be able to incorporate the experi-
ence of the operators (De Miguel, L. J., Blazquez,
L. F., 2005). To achieve such an aim, researchers
have resorted to the use of fuzzy reasoning which al-
lows symbolic generalization of numerical data using
fuzzy rules, and which supports direct integration of
operator’s experience in the decision-making process
of FDI in order to achieve more reliable fault diagno-
sis. In this paper, a PSO-trained SC-ANFIS is pro-
posed to meet the requirements for a quick and re-
liable fault detection scheme. The proposed scheme
has been evaluated on a laboratory-scale based two-
tank system. It is the most used prototype applied in
waste water treatment plants, petro-chemical plants,
and oil/gas processing plants. The main contribution
of the paper is the implementation of the proposed
PSO-SC-Adaptive Neuro-Fuzzy system and its appli-
cation to the fault diagnosis problem.
3 FAULT DIAGNOSIS PROBLEM
STATEMENT
3.1 Experimental Setup and Process
Data Collection
The Benchmarked laboratory-scale two-tank process
control system has been used to collect data at a sam-
pling rate of 50 milliseconds. Hydraulic height and
liquid output flow-rate of the second tank are the in-
puts while leakage fault level on a discrete scale of 1
to 4 is the considered output. The proposed scheme is
shown in Figure 1. A Proportional Integral (PI) con-
troller works in a closed loop configuration. Data is
collected by introducing leakage fault in the closed
loop system. This is done through the pipe clogs
of the system using drainage valve between the two
tanks. The PI controller tends to treat the introduced
fault as a disturbance and acts to suppress it. The ob-
jective of the benchmark dual-tank system is to reach
a reference height of 200 ml in the second tank. The
closed-loop nature of the experiment also tends to
suppress the faults introduced in the system, thereby
making it more difficult to detect these faults.
3.2 Model of the Coupled Tank System
The physical system under evaluation is formed of
two tanks connected by a pipe. A DC motor-driven
pump supplies the fluid to the first tank and a PI con-
troller is used to control the fluid level in the second
tank by maintaining the level at 200 ml, as shown in
ICFC 2010 - International Conference on Fuzzy Computation
400

Figure 2. A step input is applied to the dc motor-
pump system to fill the first tank. Varying levels of
leakage faults are introduced and the liquid height and
the output flow-rate of the second tank are both mea-
sured. The model relating the input control signal to
the motor, u, and the flow Q
i
is given below.
Q
i
= −a
m
Q
i
+ b
m
φ(u), (1)
where a
m
and b
m
are the parameters of the motor-
pump system and φ(u) is a dead-band and saturation-
type of nonlinearity. It is assumed that the leakage Q
l
occurs in tank 1 and is given by
Q
l
= C
dl
p
2gH
1
. (2)
With the inclusion of the leakage, the liquid level sys-
tem is modeled by
A
1
dH
1
dt
= Q
i
−C
12
φ(H
1
− H
2
) −C
l
φ(H
1
), (3)
A
2
dH
2
dt
= C
12
φ(H
1
− H
2
) −C
0
φ(H
2
), (4)
where φ(.) = sign(.)
p
2g(.),Q
l
= C
l
φ(H
1
) is the
leakage flow rate, Q
0
= C
0
φ(H
2
) is the output flow
rate, H
1
is the height of the liquid in tank 1, H
2
is the
height of the liquid in tank 2, A
1
and A
2
are the cross-
sectional areas of the 2 tanks, g = 980cm/sec
2
is the
gravitational constant, C
12
and C
0
are the discharge
coefficient of the inter-tank and output valves respec-
tively. The model of the two-tank fluid control sys-
tem is of second order and is nonlinear with smooth
square-root type nonlinearity. For design purposes, a
linearized model of the fluid system is required and is
given as
dh
1
dt
= b
1
q
i
− (a
1
+ α)h
1
+ a
1
h
2
, (5)
dh
2
dt
= a
2
h
1
− (a
2
− β)h
2
, (6)
where h
1
and h
2
are the increments in the nominal
(leakage free) heights H
0
1
and H
0
2
b
1
=
1
A
1
, a
1
=
C
db
2
q
2g(H
0
1
− H
0
2
)
,β =
C
0
2
q
2gH
0
2
, (7)
a
2
= a
1
+
C
d0
2
q
2gH
0
2
,α =
C
dl
2
q
2gH
0
1
. (8)
The parameter indicates the amount of leakage. A PI
controller, with gains k
P
and k
I
is used to maintain the
level of Tank 2 at the desired reference input r.
˙x
3
= e = r− h
2
, (9)
u = k
P
e+ k
I
x
3
(10)
The state space model is given by:
x =

h
1
h
3
x
3
q
i

T
,
A =



−a
1
− α a
1
0 b
1
a
2
−a
2
− β 0 0
0 −1 0 0
−b
m
k
P
0 b
m
k
I
−a
m



,
B =

0 0 1 b
m
k
P

T
,
C =

1 0 0 0

,
where q
i
, q
l
, q
0
, h
1
and h
2
are the increments in Q
i
,
Q
l
, Q
0
, H
0
1
and H
0
2
respectively, the parameters a
1
and a
2
are associated with linearization whereas the
parameters α and β are respectively associated with
the leakage and the output flow rate, i.e. q
l
= αh
1
,
q
0
= βh
2
.
4 ANFIS BASED FAULT
DIAGNOSIS USING
SUBTRACTIVE CLUSTERING
Subtractive Clustering (SC) technique is used to for-
mulate an ANFIS. The procedure for Subtractive
Clustering seeks optimal data point by dividing the
data into clusters and defining a cluster center based
on the density of surrounding data points. A flowchart
for SC-ANFIS is shown in the Figure 3. A radius for
each cluster is chosen. All the data points within the
radial distance of this point are then removed in or-
der to determine the next data cluster and its center.
This process is repeated until all the data is within ra-
dial distance of a cluster center. Given proper cluster
radii, the SC algorithm finds optimal data point to de-
fine a cluster center based on the density of surround-
ing data points.
4.1 Objective Function and SC-ANFIS
Tuning
In order to stress the importance of a proper cluster
radius while performing subtractive clustering, a ran-
dom radius size is chosen for all three inputs and out-
puts. Two radii sizes of 0.7 and 0.2 are chosen at
random to develop two SC based ANFIS. However,
prediction errors for both the developed SC-ANFIS
systems with radii 0.7 and 0.2, shown in Figure 8 mo-
tivate us to tune the cluster radii in order to reduce
these high errors. For this purpose, an objective func-
tion based on squared error is minimized using PSO,
and optimal cluster radii are searched.
An objectivefunction J defined below is proposed.
A PSO-TRAINED ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM FOR FAULT CLASSIFICATION
401

Figure 2: Two tank model.
Subtractive Clustering (SC) based ANFIS
Input/Output data-sets
SC applied on initial data to extract a set of rules
Generation of initial FIS using SC
Generated FIS fed as input to ANN
Generation of SC-ANFIS
Figure 3: Flowchart for SC-ANFIS.
J =
N
∑
n=1
( ˆy(n) − y(n))
2
N
(11)
where N denotes the number of data points, ˆy(n) and
y(n) denote the n
th
sample of predicted and actual out-
puts respectively.
The problem constraints are the bounds on the size
of radii for the two inputs and one output. The prob-
lem can be formulated as
minimize J, subject to the constraints
r
min
i
≤ r
i
≤ r
max
i
, i = 1,2,3. (12)
The minimum value of r
min
1,2,3
is set to 0.1 while
the maximum values are set to half the range of re-
spective inputs and outputs giving r
max
1
= 90,r
max
2
=
2,andr
max
3
= 1.5. PSO is applied to this problem in
order to find optimal or near optimal value of r
1
,r
2
,
and r
3
.
4.2 Particle Swarm Optimization
Particle Swarm Optimization (PSO) is an evolution-
ary technique used to solve optimization problems
(Kennedy, J., Eberhart, R., 2001). It uses ’swarm in-
telligence’ and has been motivated by the behavior of
organisms that stick together in social colonies such
as school of fish and flocks of birds.
PSO based SC-ANFIS
Data initialization, pre-processing and normalization
SC-ANFIS with different cluster radii
Evaluation using cost function
PSO
Generation of optimial PSO-SC-ANFIS
Figure 4: Flowchart for hybrid PSO-SC-ANFIS scheme.
In PSO, each particle in the swarm represents a
candidate solution to the problem at hand. The par-
ticles change their positions by flying around in a
multi-dimensional search space until a relatively un-
changing position has been encountered. Each par-
ticle x
j
(t) is represented by an m dimensional vec-
tor x
j
(t) = [x
j1
(t)· ··x
jm
(t)], where m represents the
number of parameters that need to be optimized. The
velocity for the j
th
particle is represented by an m di-
ICFC 2010 - International Conference on Fuzzy Computation
402

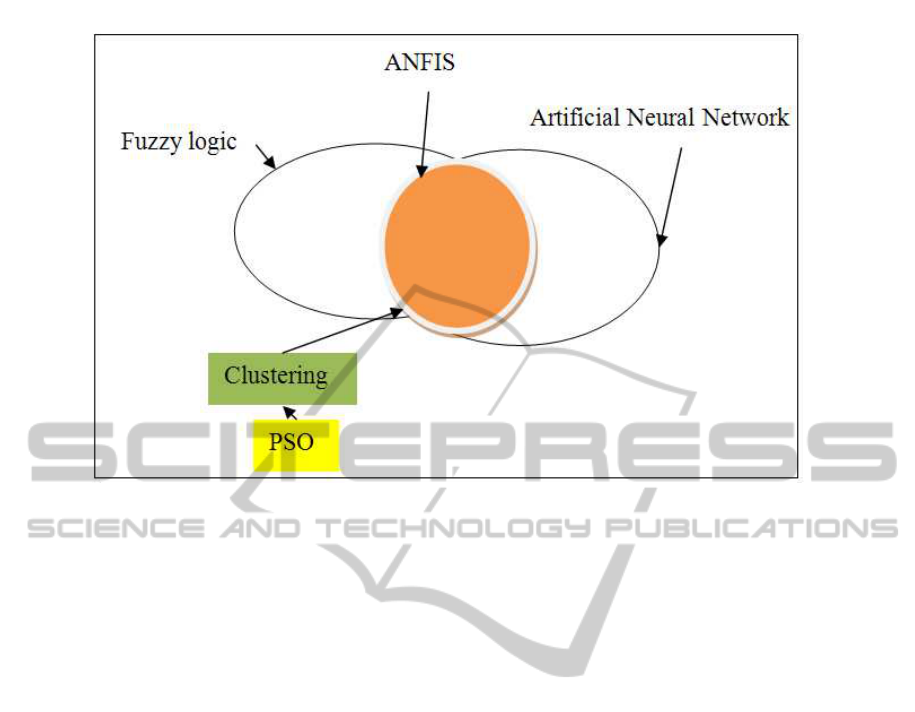
Figure 5: PSO trained SC for effective ANFIS implementation.
mensional vector v
j
(t) = [v
j1
(t)· ··v
jm
(t)]. An inertia
weight, w is used to control the impact of the previous
velocities on the current velocity. A large initial iner-
tia weight is recommended for global exploration and
vice versa. As a particle moves through the search
space, it compares its fitness value at the current posi-
tion to the best fitness value it has ever attained at any
time up to the current time. The best position that is
associated with the best fitness encountered so far is
the individual or local best x
∗
j
(t).
The global best x
∗∗
(t) is the best position
among all individual best positions achieved so far.
A random population of m dimensional particles
X(t) ε ℜ
n×m
is generated, where n denotes the size
of the population. The k
th
parameter of every parti-
cle is generated within the range of the k
th
optimized
parameter [x
max
k
,x
min
k
]. Initial velocities of particles
V(t) ε ℜ
n×m
are generated in a similar fashion. Each
particle is evaluated using an objective function J. As
the iterations progress, each particle is compared with
its local best and local best is updated. Inertia weight
is updated according to w = αw, where α is smaller
than but close to 1. Finally velocity and position of
every particle is updated. Velocity update of j
th
parti-
cle is given by
v
j
(t + 1) = wv
j
(t) + c
1
r
j1
(t){x
∗
j
(t) − x
j
(t)}
+c
2
r
j2
(t){x
∗∗
(t) − x
j
(t)}], (13)
x
j
(t + 1) = v
j
(t) + x
j
(t). (14)
where c
1
and c
2
are cognitive and social parameters
and represent orientation of velocity update towards
local and global best respectively.
4.3 Training and Performance of
PSO-ANFIS
PSO based ANFIS is developed. Flowchart for PSO-
SC-ANFIS is shown in Figure 4. A generic concept
for the implementation can be seen from the Figure
5 as well. The developed algorithm is applied on the
above defined problem to search for optimal radii of
data clusters. The number of iterations is kept 60,
population size is kept 50, cognitive and social pa-
rameters c
1
and c
2
are kept equal to 2, and constraints
on the radii, as defined above, are observed strictly.
The obtained optimal values for the three radii are
r
1
= 0.3685, r
2
= 0.1949, and r
3
= 0.1614. The con-
vergence of objective function is shown in Figure 6.
PSO converges to almost the same values of radii for
every run of the algorithm. Cost function convergence
to optimal or near optimal solution regardless of ini-
tial solution demonstrates the robustness of the algo-
rithm. Simulation result for optimal radii is shown in
Figure 7.
5 DISCUSSION
In this paper, a PSO optimized subtractive cluster-
ing is used to develop and train an ANFIS for fault
detection. The importance of using optimum clus-
ter radii can be gauged from the output error be-
tween actual faults and predicted faults shown in Fig-
ure 8. The figure shows a histogram for subtractive
A PSO-TRAINED ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM FOR FAULT CLASSIFICATION
403

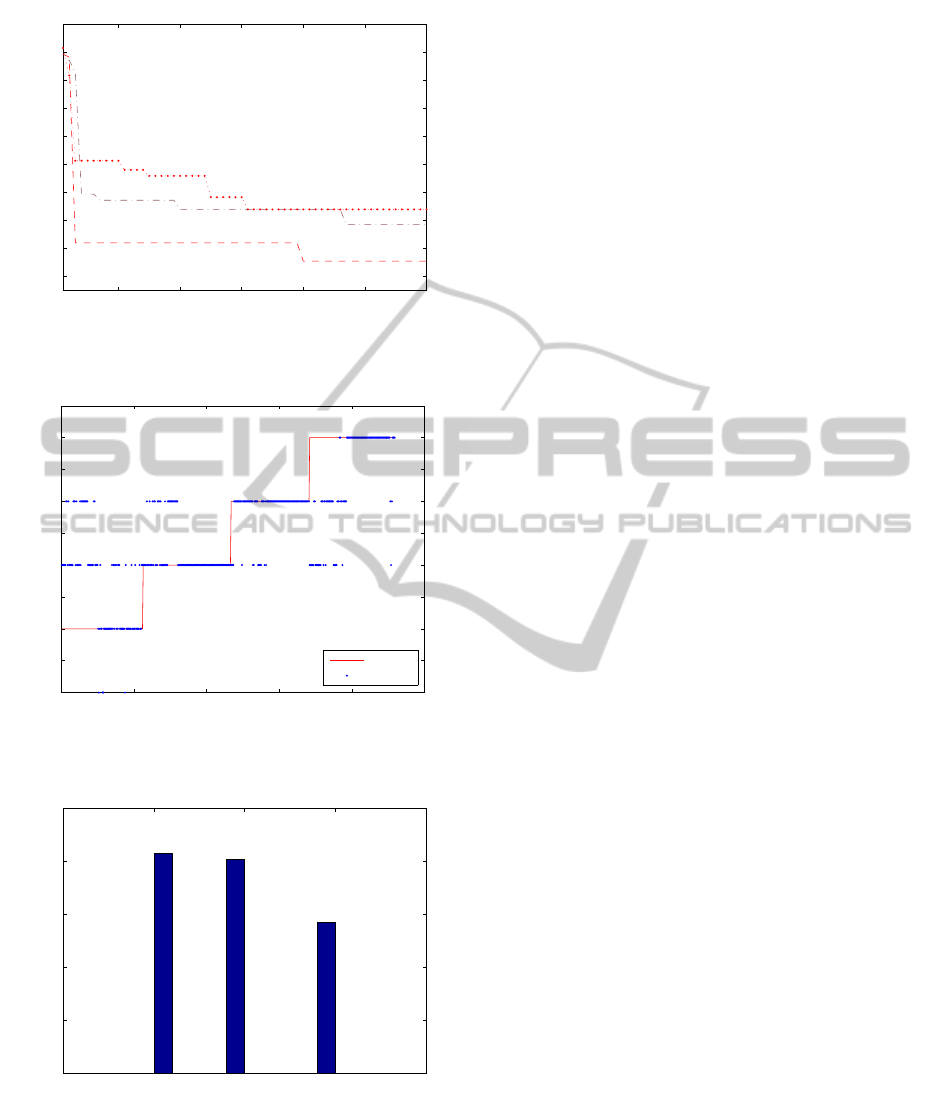
10 20 30 40 50 60
0.56
0.58
0.6
0.62
0.64
0.66
0.68
0.7
0.72
0.74
iterations
cost function J
Figure 6: Cost function convergence with different initial
solutions.
0 100 200 300 400 500
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Data Points
Fault Level
Original
Predicted
Figure 7: Leakage fault prediction results using PSO-SC-
ANFIS.
ANFIS r 1,2,3=0.2ANFIS r 1,2,3=0.7 PSO−ANFIS
0
0.2
0.4
0.6
0.8
1
mean squared prediction error
Figure 8: Prediction mean squared errors for SC-ANFIS
with randomly selected radii r
1,2,3
= 0.2,r
1,2,3
= 0.7, and
PSO-SC-ANFIS.
clustering based ANFIS with randomly selected radii
r
1,2,3
= 0.7, another ANFIS with randomly selected
radii r
1,2,3
= 0.2, and a PSO optimized subtractive
clustering based ANFIS. The error rates for the three
cases evidently place PSO-ANFIS at the top of the
other two. The error rate for PSO-ANFIS highlights
the performance of PSO in converging to a near op-
timal value for the radii of clusters. The fault detec-
tion results thus obtained are encouraging and pro-
vides motivation for more work towards further im-
provement.
ACKNOWLEDGEMENTS
The authors acknowledge support of National Sci-
ence and Engineering Research Council (NSERC),
Canada, and the Universities of New Brunswick in
Canada and KFUPM in Saudi Arabia.
REFERENCES
De Miguel, L. J., Blazquez, L. F. (2005). Fuzzy logic-
based decision-making for fault diagnosis in a dc mo-
tor. In Engineering Applications of Artificial Intelli-
gence. volume 18(4), pages 423-450.
Dou, W., Liu, Z. S., Wang, D. H. (2007). Combination
diagnosis based on genetic algorithm for rotating ma-
chinery. In Third International Conference on Neural
Computation 2007, ICNC 2007.
Duan, F., Zivanovic, R. (2009). Induction motor fault diag-
nostics using global optimization algorithm. In IEEE
Power Engineering Conference, 2009, AUPEC 2009.
pages 1-5.
Eberhart, R., Shi, Y. (1998). Parameter selection in particle
swarm optimisation. In Evolutionary Programming
VII. pages 591-600.
Elhadef, M., Ayeb, B. (2000). An evolutionary algorithm
for identifying faults in t-diagnosable systems. In The
19th IEEE Symposium on Reliable Distributed Sys-
tems, 2000. SRDS 2000. pages 74-83.
Hongxia, P., Jinying, H., Hongwei, M. (2009). Research
of fault characteristic extractive technology based on
particle swarm optimization. In Fuzz-IEEE Confer-
ence, Korea, 2009. pages 1941-1946.
Kennedy, J., Eberhart, R. (2001). Swarm Intelligence. Aca-
demic Press.
Ping, Q., Qun, L. M., Yun, M. X., Jun, W. (2009). Applica-
tion of artificial intelligence in power transformer fault
diagnosis. In IEEE 2009 International Conference on
Artificial Intelligence and Computational Intelligence.
pages 442-445.
Ping, Y. Q., Wude, X., Zhida, L. (2005). Development of an
artificial intelligent diagnosis system for transformer
fault. In IEEE/PES Transmission and Distribution
Conference & Exhibition: Asia and Pacific Dalian,
China. pages 1-5.
Wang, Y., Chan C. W., Cheung, K. C. (2001). Intelli-
gent fault diagnosis based on neuro-fuzzy networks
ICFC 2010 - International Conference on Fuzzy Computation
404

for nonlinear dynamic systems. In Proceedings of
IFAC Conference on New Technologies for Computer
Control 2001, Hong Kong, China. pages 101-104.
Wei, D., Sheng, L. Z., Xiaowei, W. (2007). Application
of image recognition based on artificial immune in ro-
tating machinery fault diagnosis. In The 1st Interna-
tional Conference on Bioinformatics and Biomedical
Engineering, 2007. ICBBE 2007. pages 1047-1052.
Zhang, G. Q. P. (2000). Neural networks for classification:
a survey. In IEEE Transactions on Systems, Man and
Cybernetics: Part C-Applications and Reviews. vol-
ume 30(4), pages 451-462.
A PSO-TRAINED ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM FOR FAULT CLASSIFICATION
405