
NEURAL NETWORK BASED HAMMERSTEIN
SYSTEM IDENTIFICATION
USING PARTICLE SWARM SUBSPACE ALGORITHM
S. Z. Rizvi and H. N. Al-Duwaish
Department of Electrical Engineering, King Fahd Univ. of Petroleum & Minerals, Dhahran, Saudi Arabia
Keywords:
Particle swarm optimization, Neural network training, Subspace identification, Static nonlinearity, Dynamic
linearity, Radial basis function (RBF) neural networks.
Abstract:
This paper presents a new method for modeling of Hammerstein systems. The developed identification method
uses state-space model in cascade with radial basis function (RBF) neural network. A recursive algorithm
is developed for estimating neural network synaptic weights and parameters of the state-space model. No
assumption on the structure of nonlinearity is made. The proposed algorithm works under the weak assumption
of richness of inputs. The problem of modeling is solved as an optimization problem and Particle Swarm
Optimization (PSO) is used for neural network training. Performance of the algorithm is evaluated in the
presence of noisy data and Monte-Carlo simulations are performed to ensure reliability and repeatability of
the identification technique.
1 INTRODUCTION
The Hammerstein Model belongs to the family of
block oriented models and is made up of a memory-
less nonlinear part followed by a linear dynamic part
as shown in Figure 1. It has been known to effectively
represent and approximate several nonlinear dynamic
industrial processes, for example pH neutralization
process (Fruzzetti, K. P., Palazoglu A., McDonald,
K. A., 1997), heat exchanger (Eskinat, E., Johnson,
S. H., Luyben, W. L., 1991), nonlinear filters (Had-
dad, A. H., Thomas, J. B., 1968), and water heater
(Abonyi, I., Nagy, L., Szeifert, E., 2000).
Figure 1: Block diagram of a Hammerstein model.
A lot of research has been carried out on identi-
fication of Hammerstein models. Hammerstein Sys-
tems can be modeled by employing either nonpara-
metric or parametric models. Nonparametric mod-
els represent the system in terms of curves result-
ing from expansion of series such as the Volterra se-
ries or kernel regression. Parametric representations
are more compact having fewer parameters. Notable
parametric identification techniques can be found in
(Narendra, K. S., Gallman, P., 1966), (Billings, S.,
1980), (Al-Duwaish, H., 2001), (V¨or¨os, J., 2002),
(Wenxiao, Z., 2007) and in references therein. Non-
parametric identification techniques can be found in
several papers including, but not limited to those of
(Greblicki, W., 1989), (Al-Duwaish, H., Nazmulka-
rim, M., Chandrasekar, V., 1997), (Zhao, W., Chen,
H., 2006).
Recently, subspace identification has emerged as
a well known method for identification of linear
systems. It is computationally less complicated as
compared to conventional prediction error methods
(PEM), does not require initial estimate of a canon-
ical model like PEM and, is easily extendable to sys-
tems having multiple inputs and outputs (Katayama,
T., 2005). However, its use is restricted mostly to lin-
ear systems. To make use of this, attempts have been
made to extend subspace linear identification to non-
linear systems such as Wiener and Hammerstein sys-
tems including use of static nonlinearity in the feed-
back path (Luo, D., Leonessa, A., 2002), assuming
known nonlinearity structures (Verhaegen, M., West-
wick, D., 1996), and using least squares support vec-
tor machines (Goethals, I., Pelckmans, K., Suykens,
J. A. K., Moor, B. D., 2005).
In this paper, a new subspace based method is pro-
182
Z. Rizvi S. and N. Al-Duwaish H..
NEURAL NETWORK BASED HAMMERSTEIN SYSTEM IDENTIFICATION USING PARTICLE SWARM SUBSPACE ALGORITHM.
DOI: 10.5220/0003072401820189
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
182-189
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)
posed for Hammerstein model identification, which
uses radial basis function (RBF) network in cascade
with a state-space model. A recursive algorithm is
developed for parameter estimation of the two sub-
systems.
The paper is arranged as follows. Section 2 looks
at the model structure proposed in this work. Section
3 takes a detailed look at the proposed identification
scheme. Section 4 describes the proposed algorithm
in detail and section 5 includes numerical examples,
their results, and analysis.
Throughout this paper, the following convention
is used for notations. Lower case variables represent
scalars. Lower case bold variables represent vectors.
Upper case bold letters denote matrices. The only ex-
ception to this convention is the choice of variable for
the cost function, where a more coventional J is used
to define the cost function.
2 PROPOSED MODEL
STRUCTURE
The proposed model structure in this work uses state-
space model to estimate the linear dynamic part. The
memoryless nonlinear part is modeled using an RBF
network. An RBF network is an effective type of neu-
ral network that has proved useful in applications like
function approximation and pattern recognition. A
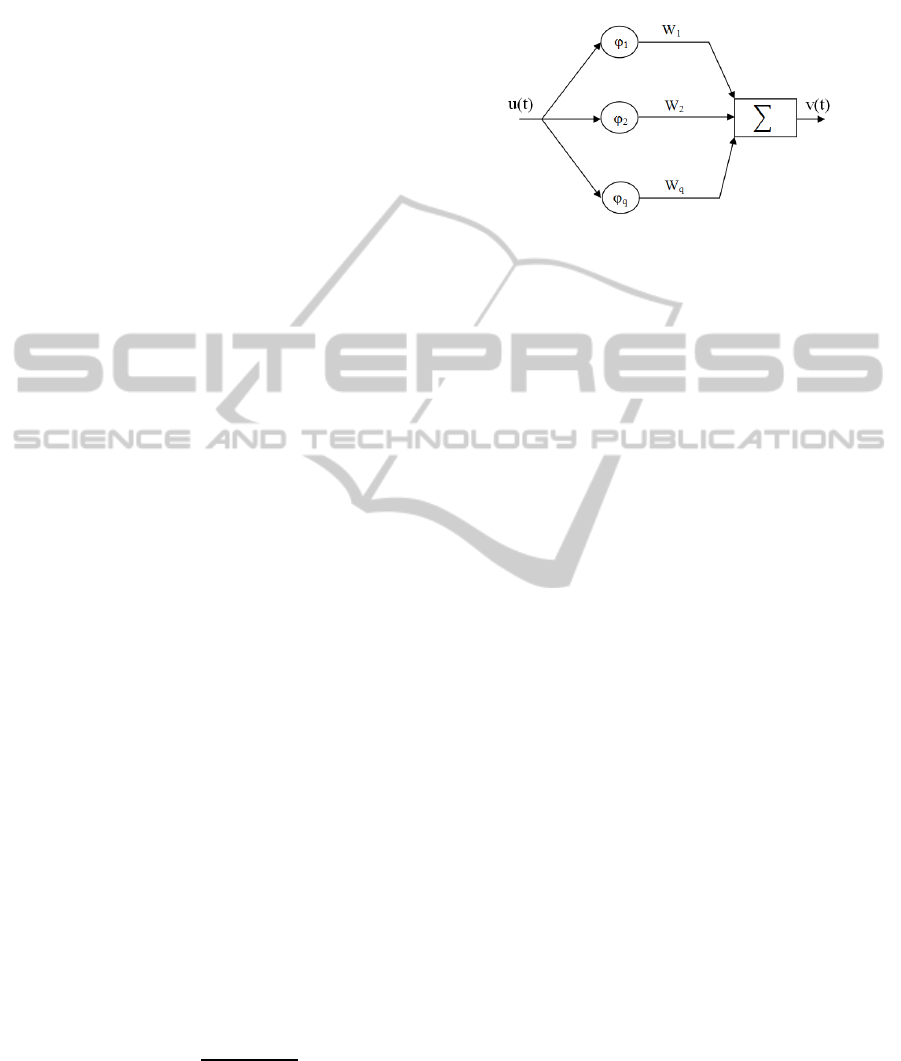
typical three layer RBF network is shown in Figure
2. The input layer connects the network to its en-
vironment. The second layer, known as the hidden
layer, performs a fixed nonlinear transformation us-
ing basis functions. The output layer linearly weighs
the response of the network to the output (Haykin,
S., 1999). The external inputs to the system u(t) are
fed to the RBF network, which generates the outputs
v(t). Considering an RBF network having q number
of neurons in the hidden layer, the basis vector is
φ(t) = [φku(t) − c
1
k···φku(t) − c
q
k],
where c
i
is the chosen center for the i
th
neuron, k.k
denotes norm that is usually Euclidean, and φ
i
is
the nonlinear radial basis function for the i
th
neuron,
given by
φ
i
(t) = exp
−
ku(t) − c
i
k
2
2σ
2
,
where σ is the spread of the Gaussian function φ
i
(t).
If the set of output layer weights of the RBF network
is given by
w = [w
1
w
2
···w
q
],
the RBF output v(t) is given by
v(t) = wφ
T
(t). (1)
Figure 2: An RBF neural network with q neurons in the
hidden layer.
Considering a system with a single input and out-
put, the output of the RBF network v(t) in turn acts as
input to the state-space model translating it into final
output y(t). The equation for y(t) is given by discrete
time state-space equation
x(t + 1) = Ax(t) + Bv(t) + w(t), (2)
y(t) = Cx(t) + Dv(t) + z(t), (3)
where v(t) and y(t) are input and output of the state-
space system at discrete time instant (t), z(t) and w(t)
are the measurement and process noise.
3 PROPOSED IDENTIFICATION
SCHEME
The problem of Hammerstein modeling is therefore
formulatedas follows. Given a set of m measurements
of noisy inputs u(t) and outputs y(t), the problem is
reduced to finding the weights of the RBF network
and the matrices of the state-space model.
For the estimation of state-space matrices, N4SID
numerical algorithm for subspace identification
(Overschee, P. V., Moor, B. D., 1994) is used. The
algorithm determines the order n of the system, the
system matrices A ε ℜ
n×n
, B ε ℜ
n×p
, C ε ℜ
r×n
, D
ε ℜ
r×p
, covariance matrices Q ε ℜ
n×n
, R ε ℜ
1×1
, S
ε ℜ
n×1
, and the Kalman gain matrix K, where p de-
notes the number of inputs and r denotes the number
of outputs of the system, without any prior knowledge
of the structure of the system, given that a large num-
ber of measurements of inputs and outputs generated
by the unknown system of equations (2) and (3) is
provided. In N4SID, Kalman filter states are first es-
timated directly from input and output data, then the
system matrices are obtained (Overschee, P. V., Moor,
B. D., 1994).
NEURAL NETWORK BASED HAMMERSTEIN SYSTEM IDENTIFICATION USING PARTICLE SWARM
SUBSPACE ALGORITHM
183

For Hammerstein identification problem, it is de-
sired that the error between the output of the actual
system, and that of the estimated model be mini-
mized. Therefore, in a way this becomes an optimiza-
tion problem where a cost index is to be minimized.
For the system described in equations (1)-(3), the cost
index is given by
J =
m
∑
t=1
e
2
(t) =
m
∑
t=1
(y(t) − ˆy(t))
2
, (4)
where y(t) and ˆy(t) are the outputs of the actual and
estimated systems at time instant (t). The weights of
the RBF network are therefore updated so as to mini-
mize this cost index. For this purpose, particle swarm
optimization (PSO) used.
PSO is a heuristic optimization algorithm which
works on the principle of swarm intelligence
(Kennedy, J., Eberhart, R., 2001). It imitates animals
living in a swarm collaborativelyworking to find their
food or habitat. In PSO, the search is directed, as ev-
ery particle position is updated in the direction of the
optimal solution. It is robust and fast and can solve
most complex and nonlinear problems. It generates
globally optimum solutions and exhibits stable con-
vergence characteristics. In this work, PSO is used to
train the RBF network. Each particle of the swarm
represents a candidate value for the weight of the out-
put layer of RBF network. The fitness of the parti-
cles is the reciprocal of the cost index given in equa-
tion (4). Hence, the smaller the sum of output errors,
the more fit are the particles. Based on this principle,
PSO updates the position of all the particles moving
towards an optimal solution for the weights of RBF
neural network.
The i
th
particle of the swarm is given by a k-
dimension vector
˜
x
i
= [ ˜x
i1
··· ˜x
ik
], where k denotes the
number of optimized parameters. Similar vectors
˜
p
i
and
˜
v
i
denote the best position and velocitiy of the i
th
particle respectively. The velocity of the i
th
particle is
updated as
˜
v
i
(t + 1) = χ[w
˜
v
i
(t) + c
1
r
1
(t){
˜
p
i
(t) −
˜
x
i
(t)}
+c
2
r
2
(t){
˜
p
g
(t) −
˜
x
i
(t)}], (5)
and the particle position is updated as
˜
x
i
(t + 1) =
˜
x
i
(t) +
˜
v
i
(t + 1). (6)
In the above equations,
˜
p
g
denotes global best posi-
tions, while c
1
and c
2
are the cognitive and social pa-
rameters respectively, and are both positive constants.
Parameter w is the inertia weight and χ is called the
constriction factor (Eberhart, R., Shi, Y., 1998). The
value of cognitive parameter c
1
signifies a particle’s
attraction to a local best position based on its past
experiences. The value of social parameter c
2
deter-
mines the swarm’s attraction towards a global best po-
sition.
4 TRAINING ALGORITHM
Given a set of m observations of input and output,
uεℜ
1×m
and yεℜ
1×m
, a hybrid PSO/Subspace iden-
tification algorithm is proposed below based on mini-
mization of output error given in equation (4).
1. Estimate state-space matrices A
0
, B
0
, C
0
and D
0
(initial estimate) from original non linear data us-
ing N4SID.
2. Iteration = k = 1.
3. Initialize PSO with random population of possible
RBF network weights.
4. w
k
= min
wεℜ
q
J (A
k−1
, B
k−1
, C
k−1
, D
k−1
, w).
5. Estimate set of RBF neural network outputs
v
k
εℜ
1×m
v
k
= w
k
Φ
T
=
w
1k
···w
qk
φ(1)
1
···φ(1)
q
.
.
.
φ(m)
1
···φ(m)
q
T
=
w
1k
···w
qk
φ(1)
.
.
.
φ(m)
T
.
6. Estimate state space matrices A
k
, B
k
, C
k
and D
k
from [v
k
, y]. This estimate of state-space model
would be an improvement on the previous esti-
mate.
7. Regenerate
ˆ
y
k
εℜ
1×m
.
8. If minimum goal is not achieved, iteration = k+ 1.
Repeat steps 3 to 7.
5 SIMULATION RESULTS
5.1 Example 1
The first example considers the following Hammer-
stein type nonlinear process whose static nonlinearity
is given by
v(t) = sign(u(t))
p
|u(t)|. (7)
The dynamic linear part is given by a third order
discrete time state-space system
A =
1.80 1 0
−1.07 0 1
0.21 0 0
, B =
4.80
1.93
1.21
,
C =
1 0 0
.
ICFC 2010 - International Conference on Fuzzy Computation
184
The eigen values of the linear subsystem lie at
λ
1
= 0.7, λ
2
= 0.6, and λ
3
= 0.5. Desired outputs
are generated by exciting the process model with a
rich set of uniformly distributed random numbers in
the interval [−1.75, 1.75]. An RBF network of 10
neurons is initialized with random synaptic weights
and centers uniformly distributed in the input inter-
val. PSO social and cognitive parameters c
1
and c
2
are kept almost equal to each other with c
1
slightly
larger than c
2
and c
1
+c
2
≥ 4 as proposed in (Carlisle,
A., Dozier, G., 2001). This allow trusting past ex-
periences as well as ample exploration of the swarm
for a global best solution. Constriction factor is kept
close to 1 to enable slow convergence with better ex-
ploration. Number of particles amount to 10 for the
synaptic weights of 10 neurons. A swarm population
size of 50 is selected and the optimization process is
run for 100 iterations.
The algorithm shows promising results and mean
squared output error between normalized outputs of
actual and estimated systems converges to a final
value of 4 × 10
−4
in 24 iterations of the algorithm.
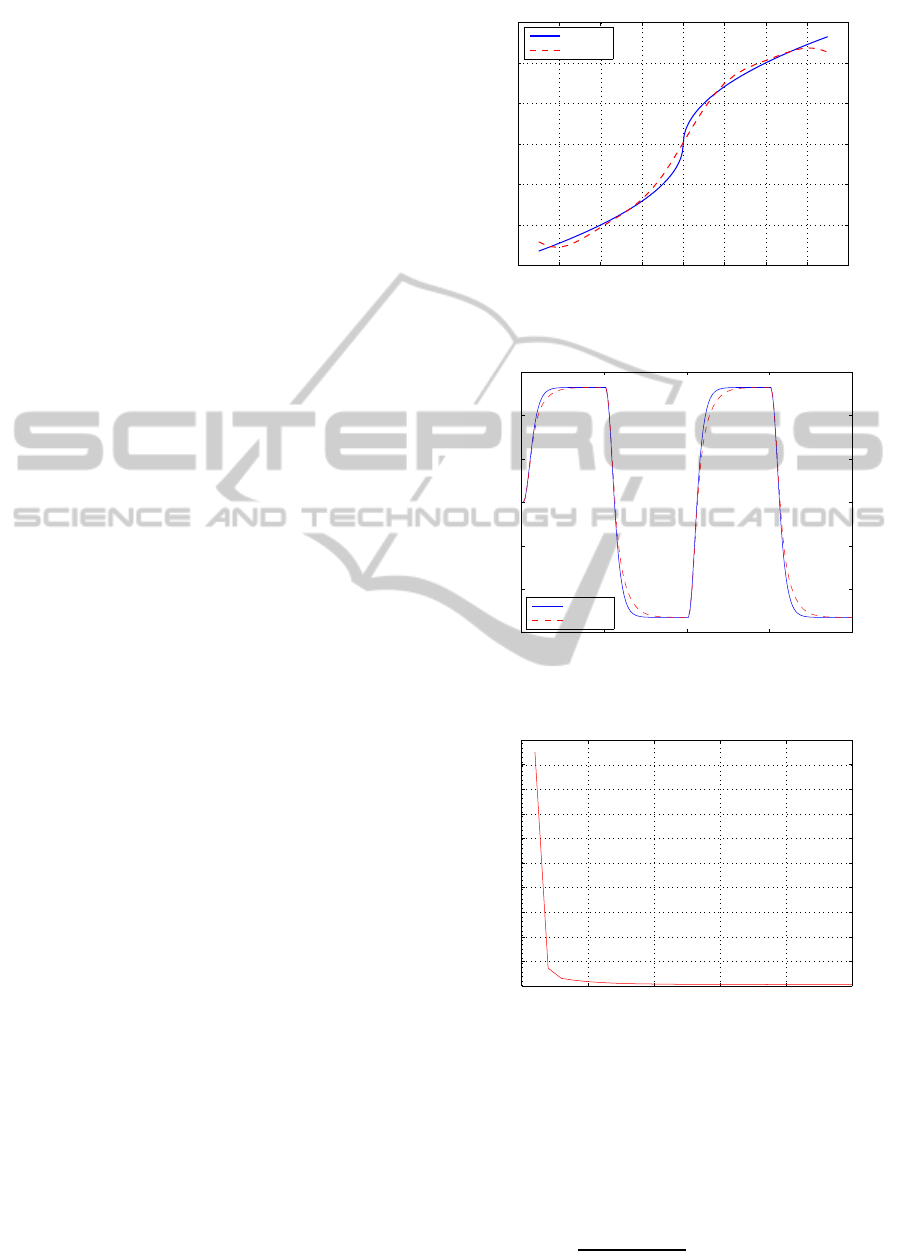
Figure 3 shows the nonlinearity estimate. Conver-
gence of mean squared error is shown in Figure 5.
An easy way to evaluate the estimate of linear dy-
namic part lies in comparing the eigen values of the
estimated system with true ones. The eigen values of
the estimated system lie at
ˆ
λ
1
= 0.72,
ˆ
λ
2
= 0.53 and
ˆ
λ
3
= 0.53. Figure 4 shows the step response of the
dynamic linear part.
To evaluate the performance of the proposed al-
gorithm in noisy environment, zero mean Gaussian
additive noise is included at the output of the system
such that the signal to noise ratio (SNR) is 10dB. The
algorithm performs well in estimating the system de-
spite low output SNR. The final mean squared error
converges to 1.4 × 10
−3
in 30 iterations. Nonlinear-
ity estimate is shown in Figure 6. The eigen values of
the estimated system lie at
ˆ
λ
10dB
1
= 0.73,
ˆ
λ
10dB
2
= 0.73
and
ˆ
λ
10dB
1
= 0.58.
The results presented above are obtained from a
single run of estimation algorithm. To further en-
sure the reliability and repeatability of the algorithm,
Monte-Carlo simulation is carried out and ensem-
ble statistics are tabulated in Table 1. The statistics
show encouraging convergence of normalized output
squared error and estimation of linear subsystem. Pa-
rameters of the nonlinearity cannot be compared be-
cause of the nonparametric nature of estimation. At
best, the estimates of nonlinearity can be judged from
the shapes of estimated nonlinear function as pre-
sented in Figures 3 and 6.
−2 −1.5 −1 −0.5 0 0.5 1 1.5 2
−1.5
−1
−0.5
0
0.5
1
1.5
Input
Output
Original
Estimated
Figure 3: Estimate of square root nonlinearity of example
1.
0 50 100 150 200
−150
−100
−50
0
50
100
150
time samples
output
original
estimated
Figure 4: Step response of linear dynamic part of example
1.
0 5 10 15 20 25
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
0.05
Iterations
Mean Squared Error
Figure 5: Mean squared error for example 1.
5.2 Example 2
The second example considers the following Ham-
merstein type nonlinear process whose static nonlin-
earity is given by
v(t) = tanh[2u(t)] 1.5 ≥ u(t),
v(t) =
exp(u(t)) − 1
exp(u(t)) + 1
4 > u(t) > 1.5.
NEURAL NETWORK BASED HAMMERSTEIN SYSTEM IDENTIFICATION USING PARTICLE SWARM
SUBSPACE ALGORITHM
185

Table 1: Monte-Carlo simulation statistics for example 1.
Estimation results without output noise
Total number of runs 200
Magnitude of actual eigen value λ
1
of linear subsystem 0.7
Mean magnitude of estimated eigen value
ˆ
λ
1
of linear subsystem 0.713
Variance of eigen value estimate
ˆ
λ
1
8× 10
−4
Magnitude of actual eigen value λ
2
of linear subsystem 0.6
Mean magnitude of estimated eigen value
ˆ
λ
2
of linear subsystem 0.62
Variance of eigen value estimate
ˆ
λ
2
4.5× 10
−3
Magnitude of actual eigen value λ
3
of linear subsystem 0.5
Mean magnitude of estimated eigen value
ˆ
λ
3
of linear subsystem 0.481
Variance of eigen value estimate
ˆ
λ
3
5.7× 10
−3
Average number of iterations required for every run 8.26
Average mean squared output error (MSE) 9.8× 10
−4
Estimation results with output SNR 10dB
Total number of runs 200
Magnitude of actual eigen value λ
1
of linear subsystem 0.7
Mean magnitude of estimated eigen value
ˆ
λ
1
of linear subsystem 0.75
Variance of eigen value estimate
ˆ
λ
1
1.6× 10
−3
Magnitude of actual eigen value λ
2
of linear subsystem 0.6
Mean magnitude of estimated eigen value
ˆ
λ
2
of linear subsystem 0.68
Variance of eigen value estimate
ˆ
λ
2
6× 10
−3
Magnitude of actual eigen value λ
3
of linear subsystem 0.5
Mean magnitude of estimated eigen value
ˆ
λ
3
of linear subsystem 0.4
Variance of eigen value estimate
ˆ
λ
3
6× 10
−2
Average number of iterations required for every run 8.02
Average mean squared output error (MSE) 6.6× 10
−3
The dynamic linear part is given by the following sec-
ond order discrete time state-space system
A =
1.0 1.0
−0.5 0.0
, B =
1
0.5
,
C =
1 0
.
The linear part of the system has eigen values at
λ
1,2
= 0.5 ± 0.5i. Desired outputs are generated by
exciting the process model with a rich set of uni-
formly distributed random numbers in the interval
[0, 4]. An RBF network with 25 neurons is initial-
ized with random synaptic weights and uniformly dis-
tributed centers chosen within the input interval. PSO
social and cognitive parameters and constriction fac-
tor are kept similar to example 1. The number of par-
ticles is equal to the number of neurons and a popula-
tion size of 50 gives good results again. The algorithm
ICFC 2010 - International Conference on Fuzzy Computation
186
−2 −1.5 −1 −0.5 0 0.5 1 1.5 2
−1.5
−1
−0.5
0
0.5
1
1.5
input
output
original
estimated
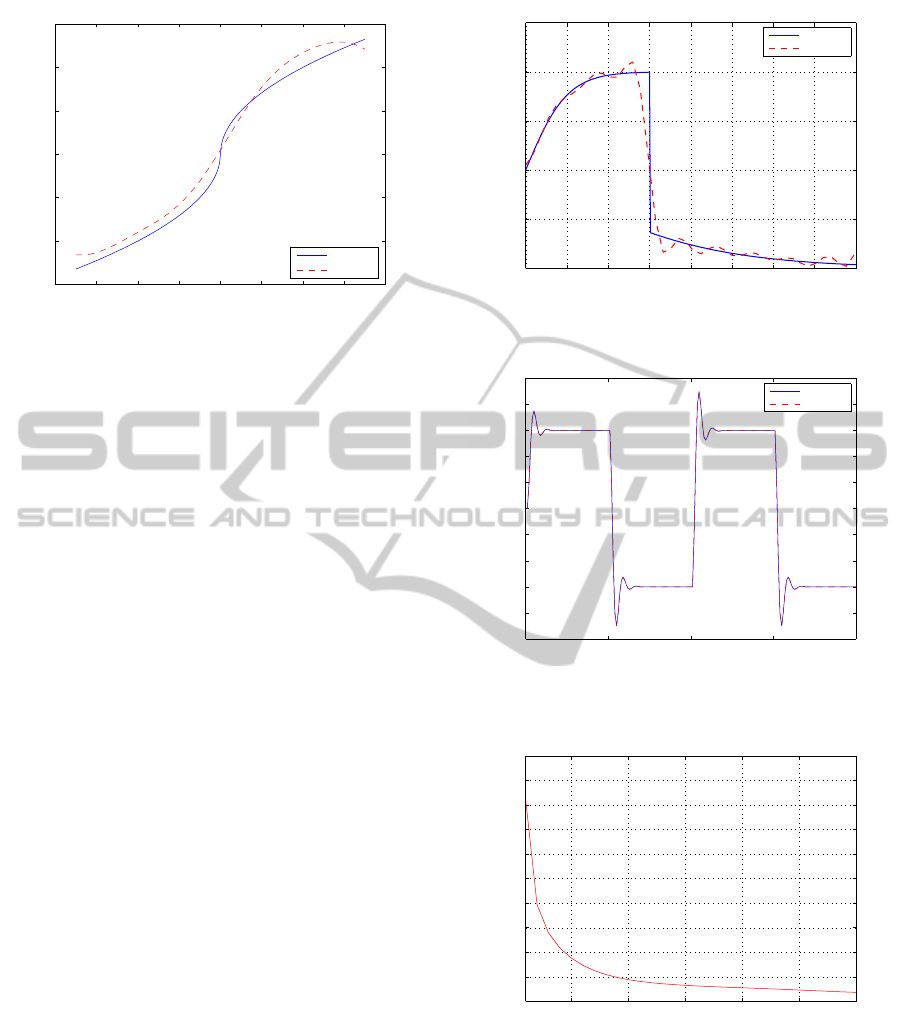
Figure 6: Estimate of square root nonlinearity of example 1
with output SNR 10dB.
performs well and estimates the system in 20 itera-
tions. The mean squared output error between nor-
malized values of actual and estimated outputs con-
verges to a final value of 8 × 10
−4
. The estimate of
nonlinearity shape is shown in Figure 7. Eigen val-
ues of the estimated system lie at
ˆ
λ
1,2
= 0.497± 0.5i.
Step response of linear subsystem is shown in Figure
8. The squared error convergence plot is shown in
Figure 9.
Estimation is then carried out in noisy environ-
ment, with zero mean Gaussian additive noise in-
cluded at the output of the system such that the sig-
nal to noise ratio (SNR) is 10dB. The algorithm per-
forms well in noisy environment. The final mean
squared error converges to 1.8× 10
−3
in 30 iterations.
Nonlinearity estimate is shown in Figure 10. The
eigen values of the estimated system lie at
ˆ
λ
10dB
1,2
=
0.493± 0.499i.
Table 2 shows ensemble statistics of Monte-Carlo
simulation for example 2. The statistics show encour-
aging convergence of normalized output squared er-
ror and estimation of linear subsystem. As mentioned
before, parameters of the nonlinearity cannot be com-
pared due to the nonparametric nature of estimation.
At best, the estimates of nonlinearity can be judged
from the shapes of estimated nonlinear function as
presented in Figures 7 and 10.
6 CONCLUSIONS
The PSO/Subspace algorithm is basically a combi-
nation of PSO and Subspace N4SID algorithm, and
hence its convergence properties are directly related
to the convergence properties of PSO and Subspace
algorithms. PSO has been usually known to per-
form better than most evolutionary algorithms (EA)s
0 0.5 1 1.5 2 2.5 3 3.5 4
−1
−0.5
0
0.5
1
1.5
Input
Output
Original
Estimated
Figure 7: Estimate of tangent-hyperbolic nonlinearity of ex-
ample 2.
0 50 100 150 200
−5
−4
−3
−2
−1
0
1
2
3
4
5
time samples
output
original
estimated
Figure 8: Step response of linear dynamic part of example
2.
5 10 15 20 25 30
0.8
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
x 10
−3
Iterations
Mean Squared Error
Figure 9: Mean squared error for example 2.
in finding global optimum provided its parameters are
tuned properly according to the application. The sub-
space algorithm is also known for having no conver-
gence problems. Its numerical robustness is guaran-
teed because of well understood linear algebra tech-
niques like QR decomposition and singular value de-
composition (SVD). As a consequence, it does not ex-
perience problems like lack of convergence,slow con-
NEURAL NETWORK BASED HAMMERSTEIN SYSTEM IDENTIFICATION USING PARTICLE SWARM
SUBSPACE ALGORITHM
187
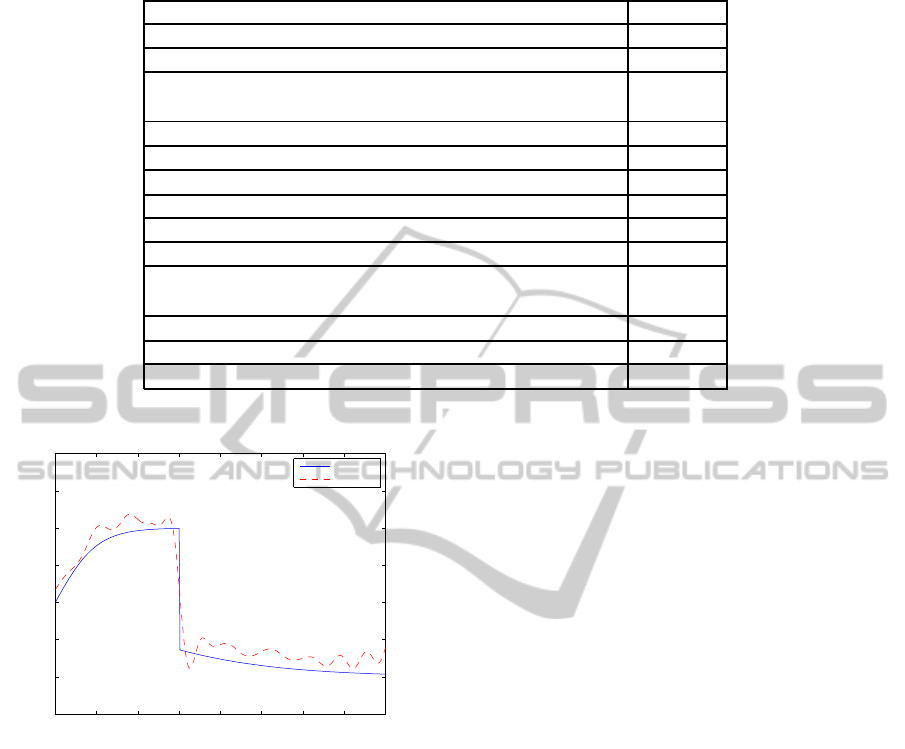
Table 2: Monte-Carlo simulation statistics for example 2
Estimation results without output noise
Total number of runs 200
Magnitude of actual eigen values λ
1,2
of linear subsystem 0.7071
Mean magnitude of estimated eigen values
ˆ
λ
1,2
of linear subsystem 0.7071
Variance of eigen value estimates 2× 10
−5
Average number of iterations required for every run 9
Average mean squared output error (MSE) 7× 10
−4
Estimation results with output SNR 10dB
Total number of runs 200
Magnitude of actual eigen values λ
1,2
of linear subsystem 0.7071
Mean magnitude of estimated eigen values
ˆ
λ
1,2
of linear subsystem 0.7079
Variance of eigen value estimates 6 × 10
−5
Average number of iterations required for every run 21
Average mean squared output error (MSE) 2 ×10
−3
0 0.5 1 1.5 2 2.5 3 3.5 4
−1.5
−1
−0.5
0
0.5
1
1.5
2
input
output
original
estimated
Figure 10: Estimate of tangent-hyperbolic nonlinearity of
example 2 with output SNR 10dB.
vergence or numerical instability (Overschee, P. V.,
Moor, B. D., 1994). Moreover, in order to assure re-
peatability and reliability of the proposed algorithm,
Monte-Carlo simulations have been carried out. The
ensemble statistics presented in Tables 1 and 2 show
strong convergenceand consistent performance of the
proposed algorithm.
The effect of noise is also studied, and the algo-
rithm is seen to converge sufficiently in the presence
of noisy data as shown in the simulation results.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the support
of King Fahd University of Petroleum & Minerals,
Dhahran, Saudi Arabia.
REFERENCES
Abonyi, I., Nagy, L., Szeifert, E. (2000). Hybrid fuzzy con-
volution modelling and identification of chemical pro-
cess systems. In International Journal Systems Sci-
ence. volume 31, pages 457-466.
Al-Duwaish, H. (2001). A genetic approach to the identifi-
cation of linear dynamical systems with static nonlin-
earities. In International Journal of Systems Science.
volume 31, pages 307-314.
Al-Duwaish, H., Nazmulkarim, M., Chandrasekar, V.
(1997). Hammerstein model identification by multi-
layer feedforward neural networks. In International
Journal Systems Science. volume 28, pages 49-54.
Billings, S. (1980). Identification of nonlinear systems - a
survey. In IEE Proceedings. volume 127, pages 272-
285.
Carlisle, A., Dozier, G. (2001). An off-the-shelf pso. In
In Proceedings of the Particle Swarm Optimization
Workshop. pages 1-6.
Eberhart, R., Shi, Y. (1998). Parameter selection in particle
swarm optimisation. In Evolutionary Programming
VII. pages 591-600.
Eskinat, E., Johnson, S. H., Luyben, W. L. (1991). Use
of hammerstein models in identification of nonlinear
systems. In AIChE Journal. volume 37, pages 255-
268.
Fruzzetti, K. P., Palazoglu A., McDonald, K. A. (1997).
Nonlinear model predictive control using hammer-
stein models. In J. Proc. Control. vol. 7, page 31-41.
Goethals, I., Pelckmans, K., Suykens, J. A. K., Moor, B. D.
(2005). Identification of mimo hammerstein models
using least squares support vector machines. In Auto-
matica. volume 41, pages 1263-1272.
ICFC 2010 - International Conference on Fuzzy Computation
188

Greblicki, W. (1989). Non-parametric orthogonal series
identification of hammerstein systems. In Interna-
tional Journal Systems Science. volume 20, pages
2335-2367.
Haddad, A. H., Thomas, J. B. (1968). On optimal and sub-
optimal nonlinear filters for discrete inputs. In lEEE
Transaction on Information Theory. volume 14, pages
16-21.
Haykin, S. (1999). Neural Networks - A Comprehensive
Foundation. Prentice-Hall, Second Edition.
Katayama, T. (2005). Subspace Methods for System Identi-
fication. Springer-Verlag, London.
Kennedy, J., Eberhart, R. (2001). Swarm Intelligence. Aca-
demic Press.
Luo, D., Leonessa, A. (2002). Identification of mimo ham-
merstein systems with nonlinear feedback. In Pro-
ceedings of American Control Conference, Galesburg,
USA. pages 3666-3671.
Narendra, K. S., Gallman, P. (1966). An iterative method
for the identification of nonlinear systems using ham-
merstein model. In IEEE Transaction on Automatic
Control. volume 11, pages 546-550.
Overschee, P. V., Moor, B. D. (1994). N4sid: Sub-
space algorithms for the identification of combined
deterministic-stochastic systems. In Automatica. vol-
ume 30, pages 75-93.
V¨or¨os, J. (2002). Modeling and paramter identification of
systems with multisegment piecewise-linear charac-
teristics. In IEEE Transaction on Automatic Control.
volume 47, pages 184-188.
Verhaegen, M., Westwick, D. (1996). Identifying mimo
hammerstein systems in the context of subspace
model identification methods. In International Jour-
nal Control. volume 63, pages 331-349.
Wenxiao, Z. (2007). Identification for hammerstein sys-
tems using extended least squares algorithm. In Pro-
ceedings of 26th Chinese Control Conference, China,.
pages 241-245.
Zhao, W., Chen, H. (2006). Recursive identification for
hammerstein systems with arx subsystem. In IEEE
Transaction on Automatic Control. volume 51, pages
1966-1974.
NEURAL NETWORK BASED HAMMERSTEIN SYSTEM IDENTIFICATION USING PARTICLE SWARM
SUBSPACE ALGORITHM
189
