USING SELF-SIMILARITY TO ADAPT EVOLUTIONARY
ENSEMBLES FOR THE DISTRIBUTED CLASSIFICATION
OF DATA STREAMS
Clara Pizzuti and Giandomenico Spezzano
National Research Council (CNR), Institute for High Performance Computing and Networking (ICAR), Rende (CS), Italy
Keywords:
Genetic programming, Data mining, Classification, Ensemble classifiers, Streaming data, Fractal dimension.
Abstract:
Distributed stream-based classification methods have many important applications such as sensor data analy-
sis, network security, and business intelligence. An important challenge is to address the issue of concept drift
in the data stream environment, which is not easily handled by the traditional learning techniques. This paper
presents a Genetic Programming (GP) based boosting ensemble method for the classification of distributed
streaming data able to adapt in presence of concept drift. The approach handles flows of data coming from
multiple locations by building a global model obtained by the aggregation of the local models coming from
each node. The algorithm uses a fractal dimension-based change detection strategy, based on self-similarity
of the ensemble behavior, that permits the capture of time-evolving trends and patterns in the stream, and to
reveal changes in evolving data streams. Experimental results on a real life data set show the validity of the
approach in maintaining an accurate and up-to-date GP ensemble.
1 INTRODUCTION
Advances in networking and parallel computation
have lead to the introduction of distributed and par-
allel data mining (DPDM). The goal of DPDM al-
gorithms is how to extract knowledge from differ-
ent subsets of a dataset and integrate these generated
knowledge structures in order to gain a global model
of the whole dataset.
This goal can be achieved in two different ways
that can be considered complementary. The first is
mining inherently distributed data where data must be
processed in their local sites because of several con-
straints such as the storage and computing costs, com-
munication overhead and privacy. The second context
is scaling up used algorithms; in this case, data set
can be partitioned and distributed through different
sites and then data mining process is applied simul-
taneously on smaller data subsets.
Distributed classification is an important task of
distributed data mining that uses a model built from
historical data to predict class labels for new observa-
tions. More and more applications are featuring data
streams, rather than finite stored data sets, which are
a challenge for traditional classification algorithms.
The design and development of fast, scalable, and ac-
curate techniques, able to extract knowledge from
huge data streams poses significant challenges (Ab-
dulsalam et al., 2008). In fact, traditional approaches
assume that data is static, i.e. a concept, represented
by a set of features, does not change because of
modifications of the external environment. In many
real applications, instead, a concept may drift due to
several motivations, for example sensor failures, in-
creases of telephone or network traffic. Concept drift
(Wang et al., 2003) can cause serious deterioration of
the performance. In such a case the adopted method
should be able to adjust quickly to changing condi-
tions. Furthermore, data that arrives in the form of
continuous streams usually is not stored, rather it is
processed as soon as it arrives and discarded right
away. Incremental or online methods (Gehrke et al.,
1999; Utgoff, 1989) are an approach to large-scale
classification on evolving data streams. These meth-
ods build a single model that represents the entire
data stream and continuously refine this model as data
flows. If data comes from different locations, it is
necessary to gather all the data on a single location
before processing. However, maintaining a unique
up-to-date model might preclude valuable older infor-
mation to be used since it is discarded as new one ar-
rives. Furthermore, incremental methods are not able
176
Pizzuti C. and Spezzano G..
USING SELF-SIMILARITY TO ADAPT EVOLUTIONARY ENSEMBLES FOR THE DISTRIBUTED CLASSIFICATION OF DATA STREAMS.
DOI: 10.5220/0003074901760181
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 176-181
ISBN: 978-989-8425-31-7
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

to capture new trends in the stream. Another prob-
lem is that these methods are not applicable in cases
where the data, computation, and other resources are
distributed and cannot be centralized for a variety of
reasons e.g. low bandwidth, security, privacy issues,
and load balancing.
In this paper we approach the problem of large-
scale distributed streaming classification by building
an adaptive GP ensemble of classifiers (Street and
Kim, 2001) that combine the results of GP clas-
sifiers, trained on nodes of a distributed network,
each containing their own local streaming data. The
learned local models are obtained by using Genetic
Programming, that inductively generate decision trees
trained on different parts of the distributed trained
set (Cant´u-Paz and Kamath, 2003). The method,
named StreamGP, assumes that data is distributed,
non-stationary, i.e. a concepts may drift, and arrives
in the form of multiple streams. StreamGP is an adap-
tive GP boosting algorithm (Iba, 1999) for classifying
data streams that applies a co-evolutionary architec-
ture to support a cooperative model of GP. StreamGP
is enriched with a change detection strategy that per-
mits the capture of time-evolving trends and patterns
in the stream, and to reveal changes in evolving data
streams. The strategy evaluates online accuracy de-
viation over time and decides to recompute the en-
semble if the deviation has exceeded a pre-specified
threshold. It is based on self-similarity of the ensem-
ble behavior, measured by its fractal dimension, and
allows revising the ensemble by promptly restoring
classification accuracy.
The method is efficient for two main reasons.
First, each node of the network works with its local
data, and communicate only the local model com-
puted with the other peer-nodes to obtain the results.
Second, once the ensemble has been built, it is used
to predict the class membership of new streams of
data and updated only when concept drift is detected.
This approach, also called deferred update (Valizade-
gan and Tan, 2007), rebuilds the model only when
there are significant changes in the distribution of
data. It requires a change detection mechanism to de-
terminate whether the current model is obsolete. This
means that each data block is scanned at most twice.
The first time to predict the class label of the examples
contained in that block. The second scan is executed
only if the ensemble accuracy on that block is sensi-
bly below the value obtained so far. In such a case,
the StreamGP algorithm is executed to obtain a new
set of classifiers to update the ensemble. Experimen-
tal results on a real life data set show the validity of
the approach.
The paper is organized as follows. The next sec-
tion presents the software architecture of the basic GP
ensemble algorithm. Section 3 describes the fractal
dimension method to detect concept drift. Section 4
illustrates the StreamGP algorithm. In section 5, fi-
nally, the results of the method on a real life data set
are presented.
2 THE SOFTWARE
ARCHITECTURE OF GP
ENSEMBLE ALGORITHM
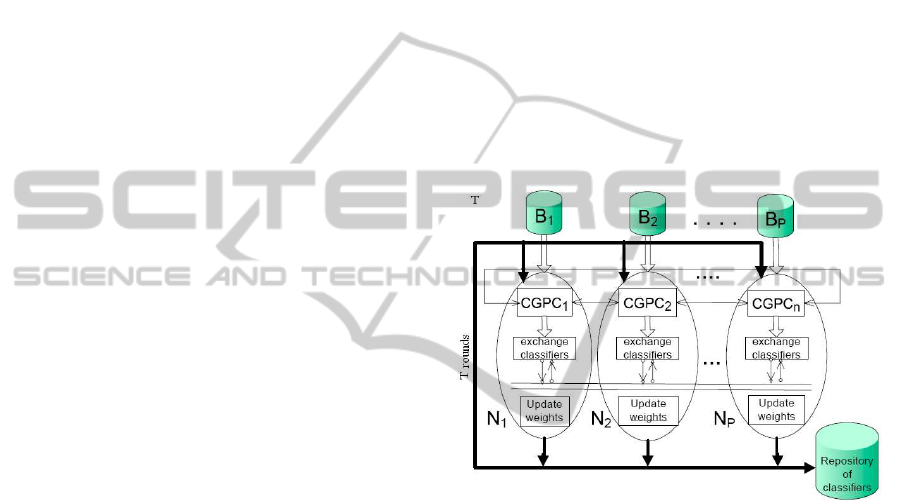
In figure 1 is shown the architecture that illustrates
the principle of cooperation of a hybrid multi-island
model of parallel GP to generate the boosting ensem-
ble of classifiers on a distributed data set.
Figure 1: Software architecture of boosting GP ensemble
algorithm.
The classifiers of each subpopulation are trained
by using the CGPC (Cellular Genetic Programming
for data Classification) algorithm (Folino et al., 1999)
on a different subset of the overall data, and combined
together to classify new tuples by applying a majority
voting scheme.
CGPC uses a cellular model of GP to locally cre-
ate a population of predictors. In the cellular model
each individual has a spatial location, a small neigh-
borhood and interacts only within its neighborhood.
In the architecture, each process employed to gen-
erate the GP ensemble of classifiers, is identical to
each other. It uses a small population to evolve the
decision trees by the CGPC algorithm enhanced with
a boosting technique that works on local data. The
boosting GP ensemble is iteratively built though a
fixed number T of rounds.
At each round a process generates the represen-
tative classifier by iterating for a certain number of
generations. The processes evolve their subpopula-
USING SELF-SIMILARITY TO ADAPT EVOLUTIONARY ENSEMBLES FOR THE DISTRIBUTED
CLASSIFICATION OF DATA STREAMS
177

tion with their own CGPC algorithm and let the out-
ermost individuals migrate to other processes using a
ring-based topology. The selection rule, the replace-
ment rule and migration strategy are specified in the
CGPC algorithm. A more formal description of the
boosting GP ensemble algorithm, in pseudo-code, is
shown in figure 2.
Given the training set S = {(x
1
,y
1
),.. .(x
N
,y
N
)}
and the number P of processors used to run the algo-
rithm, we partition the population of classifiers in P
subpopulations, and create P subsets of tuples of size
n < N by uniformly sampling instances from S with
replacement. For each process N
j
, j=1,2...p of the net-
work, a subpopulation Q
j
is initialized with random
individuals. Each subpopulation is evolved for k gen-
erations and trained on its local subset of tuples by
running CGPC.
Given S = {(x
1
,y
1
),... (x
N
,y
N
)}, x
i
∈ X
with labels y
i
∈ Y = {1,2,... ,c}, and a population Q of size q
Let B = {(i,y), i ∈ {1,2,... ,c},y 6= y
i
}
For j = 1, 2, ..., P (for each processor in parallel)
Draw a sample S
j
with size n for processor j
Initialize the weights w
1
i,y
=
1
|B|
for i = 1,. . . , n, y ∈ Y,
where n is the number of training examples on each processor j.
Initialize the subpopulation Q
i
, for i = 1,.. . , P
with random individuals
end parallel for
For t = 1,2,3, ..., T
For j = 1, 2, . . ., P (for each processor in parallel)
Train CGPC on the sample S
j
using a weighted
fitness according to the distribution w
t
Compute a weak hypothesis h
j,t
: X ×Y → [0,1]
Exchange the hypotheses h
j,t
among the P processors
Compute the error ε
t
j
=
1
2
∑
(i,y)∈B
w
t
i,y
· (1− h
j,t
(x
i
,y
i
) + h
j,t
(x
i
,y))
if ε
t
j
≥ 1/2 break loop
Set β
t
j
= ε
t
j
/(1− ε
t
j
),
Update the weights w
t
: w
t+1
i,y
=
w
t
i,y
Z
t
· β
(
1
2
)·(1+h
j,t
(x
i
,y
i
)−h
j,t
(x
i
,y))
where Z
t
is a normalization constant (chosen so that w
t
i,y
be a distribution)
end parallel for
end for t
output the hypothesis :
h
f
= arg max (
∑
p
j
∑
T
t
log(
1
β
t
j
)h
j,t
(x,y))
Figure 2: The boosting GP ensemble algorithm.
After k generations, from each subpopulation the
tree having the best fitness is chosen as representative
and output as the hypothesis computed. Then the p
individuals computed are exchanged among the nodes
of the network and constitute the ensemble of predic-
tors used to determinate the weights of the examples
for the next round (Schapire, 1996). A copy of the
ensemble is stored in a repository. During the boost-
ing rounds, each process maintains the local vector
of the weights that directly reflect the prediction ac-
curacy on that site. After the execution of the fixed
number T of boosting rounds, the classifiers stored in
the repository are used to evaluate the accuracy of the
classification algorithm using the test data.
The evolutionary process is cooperative because
the fitness of an individual of a population is calcu-
lated using the representative individuals of each one
of the other populations. These representative trees
constitute the GP ensemble used to update the weights
associated with the local examples.
3 FRACTAL DIMENSION TO
DETECT CONCEPT DRIFT
The detection of changes in data streams is known to
be a difficult task. When no information about the
data distributionis available, an approach to cope with
this problem is to monitor the performance of the al-
gorithm by using the classification accuracy as a per-
formance measure. The decaying of the predictive
accuracy below a predefined threshold can be inter-
preted as a signal of concept drift. In such a case,
however, the threshold must be tailored for the par-
ticular data set, since intrinsic accuracy can depends
on background data. Furthermore, a naive test on ac-
curacy not take into account if the decrease is mean-
ingful with respect to the past history. We propose a
more general approach to track ensemble behavior by
means of the concept of fractal dimension computed
on the set of the most recent accuracy results.
Fractals (Mandelbrot, 1983) are particular struc-
tures that present self-similarity, i. e. an invariance
with respect to the scale used. Self-similarity can be
measured using the fractal dimension. Intuitively, the
fractal dimension measures the number of dimensions
filled by the objects represented by the data set. It
can be computed by embedding the data set in a d-
dimensional grid whose cells have size r and comput-
ing the frequency p
i
with which data points fall in the
i-th cell. The fractal dimension D (Grassberger, 1983)
is given by the formula
D
q
=
(
∂log
∑
i
p
i
logp
i
∂log r
for q=1
∂log
∑
i
p
q
i
∂log r
otherwise
Among the fractal dimensions, the Hausdorff
fractal dimension (q=0), the Information Dimension
(q=1), and Correlation dimension (q=2) are the most
used. The Information and Correlation dimensions
are particularly interesting for data mining because
the numerator of D
1
is the Shannon’s entropy, and
D
2
measures the probability that two points chosen
ICEC 2010 - International Conference on Evolutionary Computation
178

at random will be within a certain distance of each
other. Changes in the Information and Correlation di-
mensions mean changes in the entropy and the distri-
bution of data, thus they can be used as an indicator of
changes in data trends. Fast algorithms exist to com-
pute the fractal dimension. The most known is the
FD3 algorithm of (Sarraille and DiFalco, 1990) that
implements the box counting method (Liebovitch and
Toth, 1989).
4 THE STREAMGP ALGORITHM
The boosting GP ensemble algorithm described is
not able to deal with concept drift of evolving data
streams. A mechanism able to detect changes of data
over time and that allows the ensemble adaptation to
such changes must be added. The mechanism used
in our algorithm is based on concepts from the Frac-
tal theory. It uses the fractal dimension as an effec-
tive method to detect a decay in the ensemble accu-
racy (i.e. self-similarity breaks down) and generates
an event to restart the training of the boosting GP en-
semble on the current data block.
The new generate ensemble is added to the current
GP ensemble by adopting a simple FIFO update strat-
egy (equivalent to preserving the most recently stored
ensemble). Figure 3 illustrates the schema adopted by
StreamGP to cope with continuous flows of data and
concept drift.
Figure 3: GP ensemble with FD-meter.
Once the ensemble E has been built, by running
the boosting method on a number of blocks, the main
aim of the adaptive StreamGP is to avoid to train
new classifiers as new data flows in until the per-
formance of E does not deteriorate very much, i.e.
the ensemble accuracy maintains above an accept-
able value. The boosting schema is extended to cope
with continuous flows of data and concept drift as
follows. Let M be the fixed size of the ensemble
E = {C
1
,.. .,C
M
}. To this end, as data comes in, the
ensemble prediction is evaluated on these new chunks
of data, and augmented misclassification errors, due
to changes in data, are detected by using the module
FD-meter. Suppose we have already scanned k − 1
blocks B
1
,.. .,B
k−1
and computed the fitness values
{ f
1
,.. ., f
k−1
} of the ensemble on each block. Let
F = { f
1
,.. ., f
H
} be the fitness values computed on
the most recent H blocks, and F
d
(F) be the fractal
dimension of F. When the block B
k
is examined,
let f
k
be the fitness value of the GP ensemble on it,
and F
′
= F ∪ { f
k
}. FD-meter then checks whether
| (F
d
(F) − F
d
(F
′
) |< τ) where τ is a fixed threshold.
In such a case the fractal dimension shows a variation
and an alarm of change is set. This means that data
distribution has been changed and the ensemble clas-
sification accuracy drops down. In the next section
we experimentally show that this approach is very ef-
fective for the algorithm that is able to quickly adjust
to changing conditions. When an alarm of change is
detected, the GP boosting algorithm loads the current
block and generates new classifiers. The older predic-
tors are discarded and substituted with the most recent
ones.
Algorithm StreamGP : maintaining a GP ensemble E
Given a network constituted by p nodes, each having a streaming data
set S
i
1. E = {C
1
,... ,C
M
}
2. F = { f
1
,... , f
H
}
3. for j = 1 . . .p (each node in parallel)
4. while (more Blocks)
5. Given a new block B
k
= {(x
1
,y
1
),... (x
n
,y
n
)}, x
i
∈ X
with labels y
i
∈ Y = {1, 2, ... ,d}
6. evaluate the ensemble E on B
k
and
let f
k
be the fitness value obtained
7. F
′
= F ∪ f
k
8. compute the fractal dimension F
d
(F
′
) of the set F
′
9. if | (F
d
(F) − F
d
(F
′
) |< τ)
10. Initialize the subpopulation Q
i
with random individuals
11. Initialize the example weights w
i
=
1
n
for i = 1,... , n
12. for t = 1, 2, 3, ... ,T (for each round of boosting)
13. Train CGPC on the block B
k
using a weighted
fitness according to the distribution w
i
14. Learn a new classifierC
j
t
15. Exchange the p classifiersC
1
t
,... ,C
p
t
obtained among the p processors
16. Update the weights
17. E = E ∪ {C
1
t
,... ,C
p
1
}
18. end for
19. Update E by retiring the oldest classifiers until | E |< M
20. end if
21. end while
22. end parallel for
Figure 4: The StreamGP algorithm.
USING SELF-SIMILARITY TO ADAPT EVOLUTIONARY ENSEMBLES FOR THE DISTRIBUTED
CLASSIFICATION OF DATA STREAMS
179

A detailed description of the algorithm in pseudo-
code is shown in figure 4. Let a network of p nodes
be given, each having a streaming data set. Suppose
E = {C
1
,.. .,C
M
} (step 1) is the ensemble stored so
far and F = { f
1
,.. ., f
H
} (step 2) be the fitness val-
ues computed on the most recent H blocks. As data
continuously flows in, it is broken in blocks of the
same size n. Every time a new block B
k
of data is
scanned, the ensemble E is evaluated on B
k
and the
fitness value obtained f
k
is stored in the set F
′
(steps
5-7). Let F
d
(F) be the fractal dimension of F and
F
d
(F
′
) the fractal dimension of F augmented with the
new fitness value f
k
obtained on the block B
k
(step
8). It it happens that | (F
d
(F) − F
d
(F
′
) |< τ) (step 9),
where τ is a fixed threshold, then a change is detected,
and the ensemble must adapt to these changes by re-
training on the new block B
k
. To this end the boosting
standard method is executed for a number T of rounds
(steps 10-18). For every node N
i
, i = 1, ... , p of the
network, a subpopulation Q
i
is initialized with ran-
dom individuals (step 10) and the weights of the train-
ing instances are set to 1/n, where n is the data block
size (step 11). Each subpopulation Q
i
is evolved for T
generations and trained on its local block B
k
by run-
ning a copy of the CGPC algorithm (step 13). Then
the p individuals of each subpopulation (step 14) are
exchanged among the p nodes and constitute the en-
semble of predictors used to determine the weights of
the examples for the next round (steps 15-17). If the
size of the ensemble is more than the maximum fixed
size M, the ensemble is updated by retiring the oldest
T × p predictors and adding the new generated ones
(step 19).
5 EXPERIMENTAL RESULTS
In this section we test our approach on the KDD Cup
1999 Data set
1
. This data set comes from the 1998
DARPA Intrusion Detection EvaluationData and con-
tains training data consisting of 7 weeks of network-
based intrusions inserted in the normal data, and 2
weeks of network-based intrusions and normal data
for a total of 4,999,000 connection records described
by 41 characteristics. The main categories of intru-
sions are four: Dos (Denial Of Service), R2L (unau-
thorized access from a remote machine), U2R (unau-
thorized access to a local super-user privileges by
a local un-privileged user), PROBING (surveillance
and probing). The experiments were performed us-
ing a network composed by 5 1.133 Ghz Pentium III
nodes having 2 Gbytes of Memory, interconnected
1
http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.
html
over high-speed LAN connections. For the experi-
ment we divided the data set in blocks of size 1k.
On each node the algorithm receives a stream of 500
blocks, thus processing 500k tuples. Figure 5 shows
the classification accuracy and the value of the fractal
dimension when an ensemble of size 50 is used, with
τ = 0.005. The figure points out the abrupt alteration
of accuracy because of the sudden change of the class
distribution of the incoming data and the ability of the
algorithm to quickly adapt to these new conditions.
Figure 6 shows the classification accuracy of the
algorithm for an increasing number of tuples, when
different ensemble sizes are used, namely 25, 50, 100,
and 200 classifiers (cls stands for classifiers). Tuples
are expressed in millions, thus 0.5 means 500,000
tuples, 1.0 one million of tuples, and so on until
2,500,000 tuples. For this data set increasing the size
of the ensemble produces improvements in classifica-
tion accuracy too, though the difference between 100
and 200 classifiers is minimal. Furthermore, the per-
centage of blocks on which the ensemble has to re-
train because of change detection is 21.82%, 19.79%,
17.28%, 17.08% respectively for ensemble size 25,
50, 100, 200.
50 100 150 200 250 300 350 400 450 500
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Number of blocks
Accuracy/Fractal dimension
Accuracy
Fractal Dimension
Figure 5: Accuracy and fractal dimension values with en-
semble size 100 and τ = 0.005 .
Figure 6: Classification accuracy for different ensemble
sizes.
ICEC 2010 - International Conference on Evolutionary Computation
180

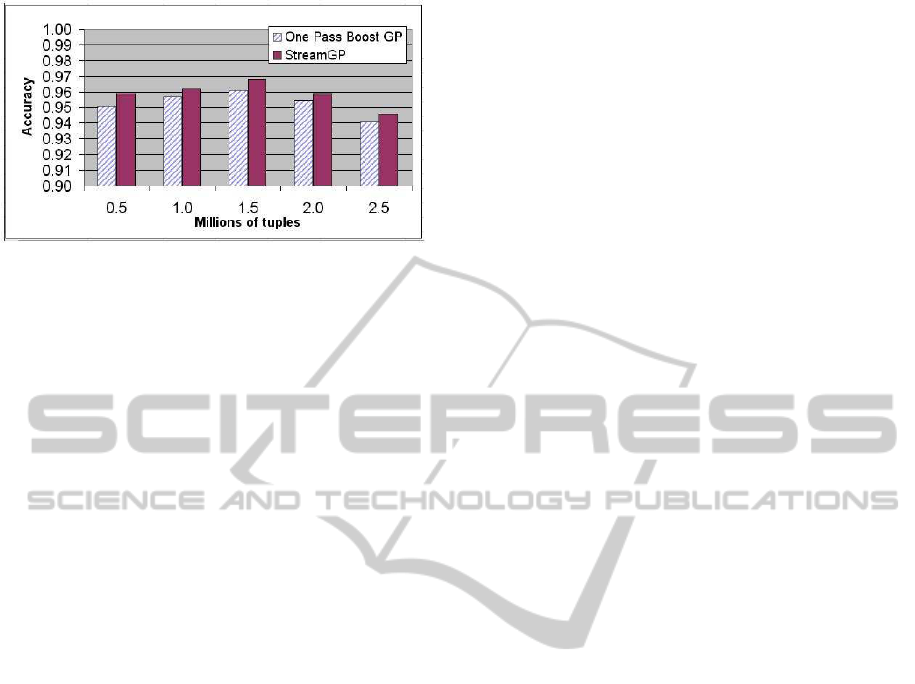
Figure 7: Accuracy comparison between StreamGP and
one-pass boosting method.
We wanted also to compare the performanceof the
algorithm against the simple one-pass algorithm that
receives the entire data set at once. To this end we run
StreamGP with an ensemble size of 50 and simulated
the one-pass boosting method by using the entire data
set scanned so far as a unique block. However, since
the boosting rounds are 5, on 5 nodes, the ensemble
generated by the one-pass method contains 25 classi-
fiers. In order to have a fair comparison, the one-pass
method had to run for 10 rounds so as to generate 50
classifiers. Figure 7 shows the classification accuracy
for an increasing number of tuples, expressed in mil-
lions. The figure point out the better performance of
the streaming approach. Another advantage to make
clear is that the streaming method works on 1k tu-
ples at a time, discarding them as soon as they have
been processed. On the contrary, the one-pass method
must maintain the entire data set considered so far,
with considerable storage and time requirements. For
example the one-pass boosting method working on
a data set of 2,500,000 tuples needs 45280 seconds,
while StreamGP, with τ = 0.01, requires 7186 sec-
onds, which is almost a magnitude order less.
6 CONCLUSIONS
The paper presented an adaptive GP boosting ensem-
ble method able to deal with distributed streaming
data and to handle concept drift via change detection.
The approach is efficient since each node of the net-
work works with its local streaming data, and the en-
semble is updated only when concept drift is detected.
REFERENCES
Abdulsalam, H., Skillicorn, D. B., and Martin, P. (2008).
Classifying evolving data streams using dynamic
streaming random forests. In DEXA ’08: Proceedings
of the 19th international conference on Database and
Expert Systems Applications, pages 643–651, Berlin,
Heidelberg. Springer-Verlag.
Cant´u-Paz, E. and Kamath, C. (2003). Inducing oblique
decision trees with evolutionary algorithms. IEEE
Transaction on Evolutionary Computation, 7(1):54–
68.
Folino, G., Pizzuti, C., and Spezzano, G. (1999). A cellular
genetic programming approach to classification. In
Proc. Of the Genetic and Evolutionary Computation
Conference GECCO99, pages 1015–1020, Orlando,
Florida. Morgan Kaufmann.
Gehrke, J., Ganti, V., Ramakrishnan, R., and Loh, W.
(1999). Boat - optimistic decision tree construction. In
Proceedings of the ACM SIGMOD International Con-
ference on Management of Data (SIGMOD’99), pages
169–180. ACM Press.
Grassberger, P. (1983). Generalized dimensions of strange
attractors. Physics Letters, 97A:227–230.
Iba, H. (1999). Bagging, boosting, and bloating in ge-
netic programming. In Proc. Of the Genetic and Evo-
lutionary Computation Conference GECCO99, pages
1053–1060, Orlando, Florida. Morgan Kaufmann.
Liebovitch, L. and Toth, T. (1989). A fast algorithm to de-
termine fractal dimensions by box counting. Physics
Letters, 141A(8):–.
Mandelbrot, B. (1983). The Fractal Geometry of Nature.
W.H Freeman, New York.
Sarraille, J. and DiFalco, P. (1990). FD3.
http://tori.postech.ac.kr/softwares.
Schapire, R. E. (1996). Boosting a weak learning by major-
ity. Information and Computation, 121(2):256–285.
Street, W. N. and Kim, Y. (2001). A streaming ensemble
algorithm (sea) for large-scale classification. In Pro-
ceedings of the seventh ACM SIGKDD International
conference on Knowledge discovery and data mining
(KDD’01),, pages 377–382, San Francisco, CA, USA.
ACM.
Utgoff, P. E. (1989). Incremental induction of decision
trees. Machine Learning, 4:161–186.
Valizadegan, H. and Tan, P.-N. (2007). A prototype-driven
framework for change detection in data stream clas-
sification. In Proc. of IEEE Symposium on Compu-
tational Intelligence and Data Mining, 2007. CIDM
2007. IEEE Computer Society.
Wang, H., Fan, W., Yu, P., and Han, J. (2003). Mining
concept-drifting data streams using ensemble classi-
fiers. In Proceedings of the nineth ACM SIGKDD In-
ternational conference on Knowledge discovery and
data mining (KDD’03),, pages 226–235, Washington,
DC, USA. ACM.
USING SELF-SIMILARITY TO ADAPT EVOLUTIONARY ENSEMBLES FOR THE DISTRIBUTED
CLASSIFICATION OF DATA STREAMS
181