
DEVELOPING MULTIVARIATE MODELS TO PREDICT
ABNORMAL STOCK RETURNS
Using Cross-sectional Differences to Identify Stocks
with Above Average Return Expectations
Alwyn J. Hoffman
School of Electrical, Electronic and Computer Engineering, Northwest University, Potchefstroom, South Africa
Keywords: Multivariate models, Stock return prediction, Neural modelling.
Abstract: This paper describes the development of multivariate models used to identify stocks with above average
return expectations. While most other research involving the development of stock return models involves
time-series prediction of future returns, this paper focuses on the modelling of cross-sectional differences
between stocks. The primary measure used in this paper to evaluate potential predictors of future stock
returns is based on sorted category returns, an approach that was previously applied to NYSE listed stocks;
in this paper the same approach is applied to stocks listed on the JSE. This measure is used to identify a
number of fundamental and technical indicators that differentiates between high and low performing stock
categories. Linear and non-linear multivariate models are subsequently developed, utilising these indicators
to improve prediction performance. It is demonstrated that much of the useful stock return behaviour is
present in the extremes of the population, that significant differences exist between different size categories,
and that different aspects of stock behaviour is exposed using appropriate measures for portfolio returns.
Portfolio performance results achieved using individual indicators as well as multivariate models are
reported and compared with previously published results, and planned future work to improve on the results
is discussed.
1 INTRODUCTION
The identification of stocks that provide above
average return expectations has not only been the
focal point of interest for market analysts but has
also received much attention in academic literature
(Fama and French, 2008; Alcock et al, 2005). Two
broad schools of thought can be identified in this
domain: while many market participants favour a
technical approach to predict future stock behaviour,
academic research in general gives preference to an
approach based on fundamental analysis to identify
stocks that are over- or undervalued (Fama and
French, 2004).
Both technical and fundamental approaches to
stock analysis usually identify a set of indicators that
are believed to have predictive capabilities regarding
future stock returns. The predictive ability of an
indicator is typically based on some kind of
hypothesis regarding the way in which the market is
believed to behave within a specific set of
circumstances. A useful indicator can be viewed as a
behavioural trait that becomes apparent before the
price of the associated stock will display some form
of predictable behaviour (typically going up or down
over a defined period of time).
Several obvious questions present themselves,
resulting from the prior discussion: how can
potential indicators of future returns be assessed and
compared objectively, and in which way can several
indicators with proven predictive ability be
combined to generate an even more useful indicator?
The purpose of this paper is to investigate an
approach to stock selection that falls somewhere
between a passive buy-and-hold strategy and an
active trading strategy involving either time series
prediction or the daily monitoring of technical
indicators as part of portfolio management. The
objective is furthermore to determine whether a
more basic approach to stock selection can produce
returns that are comparable to returns claimed to
result from time series prediction. The strategy that
is considered will require the updating of the
composition of a portfolio only once a month, based
411
J. Hoffman A..
DEVELOPING MULTIVARIATE MODELS TO PREDICT ABNORMAL STOCK RETURNS - Using Cross-sectional Differences to Identify Stocks with
Above Average Return Expectations .
DOI: 10.5220/0003075704110419
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
411-419
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

on a number of indicators of which the values tend
to change relatively slowly over time.
An innovative approach to the statistical analysis
of stock return behaviour is used, borrowing ideas
from the work reported by Fama and French (Fama
and French, 2008) in their analysis of abnormal
stock returns. This work is further extended by the
use of multivariate modelling to combine different
indicators, some fundamental and some technical in
nature, to create more representative indicators of
the medium term return expectations for specific
categories of stocks.
The data set used for this study involves all of
the stocks listed in the Johannesburg Stock
Exchange over the period March 1985 to February
2010, covering a period of 25 years. The number of
stocks for which data were available over this time
period range from about 60 during the early years up
to more than 400 by the end of the period.
The outline of the paper is as follows: Section 2
provides and overview of relevant literature and a
description of the main techniques used in the rest of
the paper. Section 3 describes the definition of and
motivation for the set of indicators used in this
study, while section 4 explores the statistical
behaviour displayed by the stocks included in this
study, and explains why the selection of optimal
portfolios is not a trivial task. The sorted returns
technique to assess the predictive ability of
indicators is described in section 5. In section 6 the
multivariate techniques used to combine individual
indicators into more comprehensive models are
described, and the challenges to extract good models
are discussed. Section 7 covers the results that were
obtained using different stock selection approaches,
and compares these against results reported
elsewhere in literature. The paper is concluded with
section 8 which provides a summary and overview
of results, as well as references to future work.
2 LITERATURE REVIEW
There has been much fundamental debate in
literature about the predictability of financial time
series, and more specifically of stock returns (Blasco
et al, 1997; Kluppelberg et al, 2002). Initial views in
favour of the efficient market hypothesis stated that
stock prices already reflect all available knowledge
about that stock, making the prediction of stock
returns to earn abnormal returns on a portfolio
impossible in principle. Much has however been
published in recent years confounding those early
views, and today it is widely accepted that the strong
form of market efficiency does not hold up in
practice (Fama and French, 2004).
Many studies have demonstrated the ability of
both linear and non-linear time series prediction
models to predict future stock behaviour, contrary to
earlier beliefs that the market behaviour should be
described as a random walk model (Lorek et al,
1983; Altay and Satman, 2005; Bekiros, 2007; Jasic
and Wood, 2004; Huang et al, 2007). An obvious
issue to be addressed is the most appropriate
benchmark against which to measure the
performance of such prediction models.
3 DEFINING THE PREDICTORS
The analyses in this paper are based on monthly
data, and returns are calculated relative to the market
index as calculated from the set of available stocks.
Returns were calculated using the change in the
baseline value of each stock, with the baseline value
being the value referred to the initial date when the
stock was first listed. The formula used to calculate
relative returns was as follows:
,
,
,
,
with RR
i,j
indicating the relative return of stock i
over period j and RelShBL
i,j
the relative share
baseline value of stock i for month j.
As will be explained in subsequent sections, this
paper will use sorted stock returns per category as
measure for the quality of a candidate predictor, a
technique that was first reported by Fama and
French (2008). For purpose of comparison the same
set of stock return predictors as defined by Fama and
French (mostly fundamental indicators) is used in
this paper, complemented by a number of additional
parameters that broadly fall in the class of ‘technical
indicators’. This paper therefore also serves the
purpose of comparing the predictive ability of
fundamental versus technical indicators, in the
process making a contribution towards the long
standing debate regarding the respective merits of
these two approaches to stock analysis.
The following list of parameters was
incorporated in the study as potential predictors of
future stock returns:
• Market capitalization (MC), defined as the
natural logarithm of the stock price multiplied
by the current number of issued shares;
• Momentum, defined as the relative return of
the stock over the period from 12 months to 1
months prior to the current date (relative return
ICFC 2010 - International Conference on Fuzzy Computation
412

Table 1: Correlation between candidate predictors and future stock returns: a comparison between time-based and cross-
sectional correlations.
Predictor Time‐basedcorrelation Cross‐sectionalcorrelation
Ave Std Ave/Std Ave Std Ave/Std
MC ‐0.0912543 0.0836058 ‐1.0914829 ‐0.1575078 0.1149865‐1.3697937
BtoM 0.1074284 0.055503 1.935544 0.0790633 0.1667667 0.4740954
Momentum 0.0043152 0.0412991 0.1044854 0.0179527 0.1187149 0.1512252
NS ‐0.0286184 0.0379534 ‐0.7540394 ‐0.0348528 0.0628141‐0.5548568
YtoB 0.0118392 0.0380539 0.3111155 0.0333755 0.1374055 0.2428976
deltaAssets ‐0.0127946 0.0171016 ‐0.7481523 0.0034774 0.0810011 0.0429297
Accr 0.0021115 0.0212071 0.0995646 0.0064688 0.0707932 0.0913755
DO 0.0122353 0.0295008 0.4147464 0.0340647 0.1442936 0.2360794
DO_RR 0.0008196 0.0385019 0.021286 0.044983 0.0964287 0.46649
being the return on the stock compared to
return on the market index);
• Book-to-market (BtoM), defined as the ratio of
the book value of equity per share to the
market value of a share;
• Net share issues (NS), defined as the logarithm
of the ratio between the current number of
shares issued by the company and the number
of shares issued 12 months ago;
• Yield-to-book (YtoB), defined as the earnings
yield per share divided by the book value per
share;
• Accruals, defined as the proportional increase
of operating assets over the past 12 months;
• Delta Assets (DAssets), defined as the
proportional increase in total assets over the
past 12 months;
• Detrended oscillator for relative share baseline
(DO_RelShBL), defined as the difference
between the short and long term moving
average of the relative share price, divided by
the maximum value of the share price over a
defined historic time period (relative share
price being the price of the stock relative to the
market index, with price at the start of the
period of evaluation serving as baseline):
_
_
_
• Detrended oscillator for relative return
(DO_RR), defined as the difference between
short and long term moving average in relative
stock returns (opposed to relative stock price
used in the calculation of DO_RelShBL):
_
_
• Historic 12 month moving average of relative
stock return over a period ending one or more
years before the current time (e.g. RR12m60 for
a 60 month delay);
• MAEY, defined as the 12 month moving
average of earnings yield on the stock (earnings
yield being the earnings per share divided by
stock price).
4 STATISTICAL BEHAVIOUR OF
THE PREDICTORS
As a first step to unravel those relationships that can
potentially form part of prediction models the linear
correlations between the identified candidate
predictors and 12 month future returns were
calculated. Two types of correlation were calculated:
firstly the correlation over time between a stock
return and an explanatory variable was determined,
repeating this calculation per stock. To obtain a
summary measure representative of the entire
population the average is taken of the time-based
correlations for all stocks. This calculation is
repeated after each period once new data has been
added to the training set. While this correlation
parameter measures the ability of an explanatory
variable to predict the future return per stock, it does
not directly measure the degree to which differences
in the indicator value between stocks is correlated
with differences in future returns for those stocks.
The alternative correlation measure, which is
generally called the cross-sectional correlation, is
calculated by correlating, for each time period, the
stock return differences between different stocks
with the differences in values of the explanatory
variable over the same set of stocks. This calculation
is also repeated after each period and the average of
all cross-sectional correlations is taken over the
entire period for which training data is available. As
DEVELOPING MULTIVARIATE MODELS TO PREDICT ABNORMAL STOCK RETURNS - Using Cross-sectional
Differences to Identify Stocks with Above Average Return Expectations
413

this correlation parameter directly measures the
ability to predict differential future returns of the
stocks, it could be expected that it would be a
superior indicator based on which to select stocks
that will on average outperform the market for the
prediction period.
As is the case with most statistical modelling
exercises, there is no guarantee that a relationship
that exists over a specific period of time will persist
during subsequent periods. For this reason the
standard deviation of correlation coefficients over
time is also calculated for both correlation measures,
to indicate how stable these measures are to detect
relationships that can be exploited over extended
time periods.
The averages and standard deviations for both
types of correlation are displayed in Table 1, for
each of the predictors as defined in the previous
section. To allow the comparative assessment of the
stability of the correlations a column is added to
display average correlation normalised with respect
to standard deviation of correlation over time.
Firstly it can be seen that the relationships
between the respective indicators and future returns
vary substantially over time: for all of the indicators,
with the exception of MC (for both correlation
types) and BtoM (for time-based correlations), the
normalised average correlations have absolute
values smaller than one. This indicates that MC
should be the most consistent indicator for above
average returns, which is in line with prior research
(Fama and French, 2008), while the other indicators
could be expected to posses less predictive power.
For some predictors, e.g. MC, the two different
correlation measures provide consistent indications
of the relationship between the predictor and future
returns. For others, e.g. DO_RR, the time-based
correlation provides no indication of predictive
capability, whereas the cross-sectional correlation,
while not being very consistent, does indicate some
predictive power for this indicator.
For most modelling exercises the order in which
predictors are added to the model is potentially of
importance. While the time-based correlations
indicate BtoM as the most significant predictor, this
role is awarded to MC when using cross-sectional
correlations.
A further question is what minimum level of
correlation, or normalised correlation, should be
sufficient to indicate consistent predictive capability,
either for the indicator in isolation or when
considering the addition of that indicator to a
existing model in combination with other indicators.
This question was addressed by using the technique
of sorted returns, which is the next topic of this
paper.
5 EVALUATING PREDICTIVE
VALUE OF INDICATORS
One of the key focal points of this paper is to
compare the different correlation measures of the
previous section with sorted returns as basis for
selecting predictor variables to be incorporated into
a prediction model. Using the same approach as
described in Fama and French (2008), the ability of
each of these parameters to explain cross-sectional
differences in returns between different stocks is
investigated as follows:
• For each of the above parameters in
succession, all stocks are sorted based on the
value of the respective parameter for each
individual stock (e.g. the first sort is done
based on MC; next a sort is done based on
Momentum, etc.).
• Once a sort has been done, the stocks are
divided into five categories, each containing
the same number of stocks, from the lowest to
the highest values for the respective sorting
parameter.
• The aggregate return for all stocks within each
sorted category is calculated, both weighted
equally as well as weighted based on market
capitalization, using the following formulas:
_
1
_
∑
∑
where RelRet(n) is the relative return of the n-th
stock, MarketCap(n) is the market
capitilazation of the n-th stock, and N is the
total number of stocks in the portfolio under
consideration.
• This process is repeated after each month, in
every case only using information that was
already available before the start of the month.
• The average return of the sorted categories is
calculated over a period of time, and the
difference between returns of the lowest and
highest sorted categories is determined:
1
ICFC 2010 - International Conference on Fuzzy Computation
414

Table 2: Sorted returns and t-statistics for candidate cross-sectional stock return predictors.
MC RR_Momentum BtoM DO_RR DO_RelShB
L
NS
Average Corr Coeff with
Predicted Return
‐0.150 0.016 0.075 0.054 0.055‐0.028
Std of Average Corr Coeff
0.115 0.119 0.165 0.091 0.135 0.053
EqW High-low Returns
All
‐0.043 0.019 0.014 0.023 0.013‐0.016
Micro
‐0.050 0.014 0.003 0.027 0.017‐0.039
Small
‐0.003‐0.116 0.018 0.009 0.017‐0.006
Big
‐0.002‐0.004 0.018 0.011 0.019‐0.005
EqW High-low
t
-statistics
All
‐8.931 4.845 2.838 4.485 2.444‐3.298
Micro
‐9.143‐0.660 0.521 4.753 2.869‐7.246
Small
‐0.584 3.006 3.984 2.014 3.400‐1.429
Big
‐0.525‐0.660 4.604 2.741 4.314‐1.135
ValW High-low Returns
All
‐0.023 0.023 0.028 0.012 0.024‐0.003
Micro
‐0.016 0.020 0.007 0.020 0.031‐0.003
Small
‐0.002 0.017 0.018 0.005 0.017‐0.003
Big
‐0.005 0.019 0.019 0.007 0.021‐0.008
ValW High-low t-statistics
All
‐5.426 5.380 6.763 2.676 5.279‐0.736
Micro
‐3.344 4.192 1.505 3.961 6.062‐0.675
Small
‐0.423 3.912 4.085 1.212 3.613‐0.574
Big
‐1.108 4.517 4.493 1.565 4.417‐1.848
where M
i
is the number of months over which
the average return is calculated, i
cat
is the i-th
sorted category for which the return is
calculated, and RelRet(m
i
) is either the equal or
the value weighted average return of all stocks
falling into that category.
• t-statistics of these high-min-low sorted returns
are calculated to determine if the returns of the
sorted stock categories differ significantly
from the return of the overall population of
stocks.
• Parameters of which the t-statistics of high-
min-low sorted returns falls outside of the
range ±1 are considered for inclusion as
predictors in the subsequent modelling
exercise.
Table 2 below displays the values of sorted returns
for the above set of candidate predictors, as well as
the t-statistics for high-min-low returns. The
predictors justifying inclusion into a stock selection
model, based on the above results, include MC,
Momentum, BtoM, NS, DO and DO_RR; three of
these can be regarded as fundamental indicators
(MC, BtoM and NS) while the other three fall into
the category of technical indicators.
The indication of predictive ability of the
respective indicators based on sorted returns differs
significantly compared to the outcome of the
analysis based on correlation coefficients. While
Momentum displayed relatively insignificant
correlation with future returns, this indicator proves
to be significant when assessed based on sorted
returns. The same is true for DO_RR, demonstrating
that there can be useful return behaviour associated
with the extreme behaviour of an indicator, even
though that indicator may not in general be well
correlated with future returns. It can furthermore be
seen that DO performs better than DO_RR for value
weighted portfolios, but that the opposite is true for
equally weighted portfolios. This indicates that DO
may be more strongly present amongst Big stocks,
with DO_RR more prominent amongst Micro
stocks. MC is clearly the most significant sorted
returns based indicator, confirming that cross-
sectional correlation is a more reliable measure
compared to time-based correlation.
6 EVALUATING THE
PREDICTORS USING A
TRADING SIMULATOR
The analysis of sorted returns as described above
does not take into account all of the practicalities
related to composing and maintaining an actual
stock portfolio. For this purpose a simulator was
developed to model the behaviour of a stock
portfolio over time, taking into account the
DEVELOPING MULTIVARIATE MODELS TO PREDICT ABNORMAL STOCK RETURNS - Using Cross-sectional
Differences to Identify Stocks with Above Average Return Expectations
415

following aspects that may impact upon the
consistence and performance of such portfolios:
• The number of stocks to be incorporated into
the portfolio (using a minimum number of
10);
• The size of the portfolio, against the
background of limited trading volumes in
some stocks, specifically micro cap stocks;
• Trading costs, setting this at 0.25%.
The simulator was used to simulate the expected
returns on portfolios using each of the candidate
predictors as criteria for stock selection. The results
are displayed in table 4 below for different initial
portfolio sizes and over different time periods when
the stock market potentially displayed different
types of behaviour.
It is clear that the simulated trading results
confirm the findings of the sorted returns analysis,
with MC providing the largest potential abnormal
stock returns. The other indicators tend to perform
differently over different time periods, each
experiencing periods of strong predictive power,
followed by periods where the relationship with
future returns tends to weaken or sometimes even
being reversed.
MC is the only predictor that retains its
predictive capabilities over the entire period of
evaluation. This performance is however only
sustained for portfolios that are small in size. What
is apparent from tables 1 and 2 is that abnormal
returns explained by MC is mostly confined to micro
caps: as soon as the portfolio size grows to a level
where most investments must be made into stocks
falling outside of the micro cap category, the
predictive capabilities of MC tend to weaken
substantially.
The above finding clearly indicates the need for
models that can combine all of the predictors into a
single measure that will be less dependent on
portfolio size and that will perform more
consistently over time. Both linear multivariate
regression and neural networks were used for this
purpose.
7 TRAINING MULTIVARIATE
MODELS
The models used in this work were limited to single
layer networks (to test the performance of linear
models combining several variables) as well as two-
layer network with one hidden layer (to determine if
non-linear models could better capture the true
cross-sectional relationships between predictors and
abnormal stock returns). In all cases the networks
were feed-forward, and used mean squared error
with Levenberg-Marquardt optimization used for
training 2 layer models. A general regression
network based on radial basis functions was also
trained to compare its performance with those of
multilayer perceptron networks.
In order to investigate the consistency of the
relationships between the predictor variables and
future returns the respective models were trained on
data sets covering different lengths of time. This will
provide an indication of how long the memory of the
market is and will indicate how often models should
be retrained. In this study models were trained with
training sets extending over periods varying from 24
months up to 120 months. Each trained model was
then applied to the next 12 months of data,
predicting returns over periods that were unseen
during the training period. This model extraction and
prediction process was repeated on a monthly basis
covering the entire period.
In each case the historic data was divided into a
training set (60% of samples), a validation set (20%)
and test set (20%). The number of input parameters
varied between 2 and 4, starting off with those
parameters that were expected to contribute the most
to predictive ability, based on the results of the
sorted returns analysis, and testing the ability of
additional variables to improve the modelled results.
The following criteria were used to assess the
performance of the respective models:
• Average correlation coefficient between target
and predicted variables over the unseen test
periods;
• Using predicted returns as sorting variable, and
then comparing the high-min-low sorted
returns;
• Finally by comparing the portfolio returns
obtained under different sets of circumstances,
using simulated portfolio returns as measure for
model performance.
8 RESULTS AND DISCUSSION
The results obtained with the different multivariate
models that were trained are displayed in table 3,
including the results for All Shares, Micro Shares,
Small Shares and Big Shares. In each case the table
displays average correlation coefficient between
actual and predicted returns, the EqW and ValW
High-min-Low sorted returns and the t-statistic for
ICFC 2010 - International Conference on Fuzzy Computation
416

Table 3: Sorted returns and t-statistics obtained with multivariate models.
Predictorsused
LinRegr LinRegr LinRegr
FFNN
Num_Std0
FFNN
Num_Std2 RBFNN
MC,BtoM,DO_RR MC,BtoM NS,BtoM,DO_RR MC,BtoM MC,BtoM
MC,BtoM,
DO_RR
NumMonthsTrain 120 24 120 24 120 24 120 120 120
Average Corr Coeff
with Predicted Return
0.138 0.118 0.115 0.125 0.072 0.054 0.084 0.105 0.119
Std of Av Corr Coeff
0.134 0.140 0.148 0.137 0.117 0.147 0.110 0.085
EqW High-
low Returns
All
0.050 0.032 0.042 0.033 0.023 0.013 0.025 0.041 0.039
Micro
0.050 0.035 0.052 0.039 0.025 0.015 0.022 0.043
Small
0.010‐0.001 0.004 0.004 0.013 0.006 0.009 ‐0.005
Big
0.008 0.002‐0.003 0.003 0.012 ‐0.001 0.006 ‐0.001
EqW High-
low t-
statistics
All
9.610 6.128 8.702 6.887 4.455 2.591 4.728 8.135 7.009
Micro
8.431 5.938 9.560 7.202 4.179 2.515 3.672 7.593
Small
1.976‐0.143 0.874 0.806 2.733 1.334 1.917 ‐1.025
Big
1.958 0.476‐0.806 0.796 2.798 ‐0.248 1.421 ‐0.139
ValW High-
low Returns
All
0.030 0.017 0.019 0.022 0.018 0.003 0.023 0.025 0.030
Micro
0.020 0.013 0.026 0.021 0.019 0.010 0.013 0.017
Small
0.009 0.000 0.003 0.004 0.009 0.007 0.007 ‐0.006
Big
0.011 0.006‐0.006 0.003 0.011 0.003 0.006 0.001
ValW High-
low t-
statistics
All
6.444 3.690 4.592 5.277 3.877 0.551 4.957 5.787 6.008
Micro
3.904 2.468 5.509 4.380 3.596 1.978 2.453 3.372
Small
1.941 0.082 0.583 0.893 1.908 1.582 1.568 ‐1.261
Big
2.271 1.247‐1.390 0.737 2.269 0.615 1.391 0.308
that sorted return.
As could be expected, given the sorted returns of
the individual predictors, the best results were
obtained using sets of predictors that included MC.
The highest EqW relative monthly high-min-low
return is obtained with a linear model using MC,
BtoM and DO_RR as inputs, and just exceeds 5%
per month relative return, which implies an annual
return in excess of 80% over market return
(excluding trading costs). The relative return earned
by this model for Micro shares only is almost the
same, while much lower returns are generated with
portfolios selected from the Small and Big share
categories (0.96% and 0.84% per month
respectively, equating to annual excess returns of
12.1% and 10.5% respectively). The very high
relative returns generated by MC is therefore only
possible for portfolios that are small enough in size
to exploit the high returns of micro caps found in the
extreme sorted categories.
It can however be noted that this model also
provides a ValW relative monthly return of 2.95%,
i.e. an annual excess return of 41.5%, for value
weighted portfolios where Micro cap shares does not
play such a dominating role. The returns produced
by this model are also higher than the returns
generated by any of the individual predictors, both
for EqW and for ValW portfolios. It furthermore
compares favourably with returns reported
elsewhere based on time-series prediction techniques
(Lorek et al, 1983; Altay and Satman, 2005; Bekiros,
2007; Jasic and Wood, 2004; Huang et al, 2007).
Table 3 also displays results for different lengths
of the training set. It is clear that longer training
periods tend to lead to more accurate models, as in
all cases the best results are achieved when training
the models over 120 months, with training over only
24 months resulting in the worst performance. It
would therefore seem that the market has a relatively
long ‘memory’, indicating that at least some
elements of the relationships between predictors and
future returns tend to persist over periods of at least
up to 10 years. Conversely the conclusion can be
made that a period of only 2 years is too short to
train an accurate model, as this period of time does
not display all types of behaviour that may occur
DEVELOPING MULTIVARIATE MODELS TO PREDICT ABNORMAL STOCK RETURNS - Using Cross-sectional
Differences to Identify Stocks with Above Average Return Expectations
417
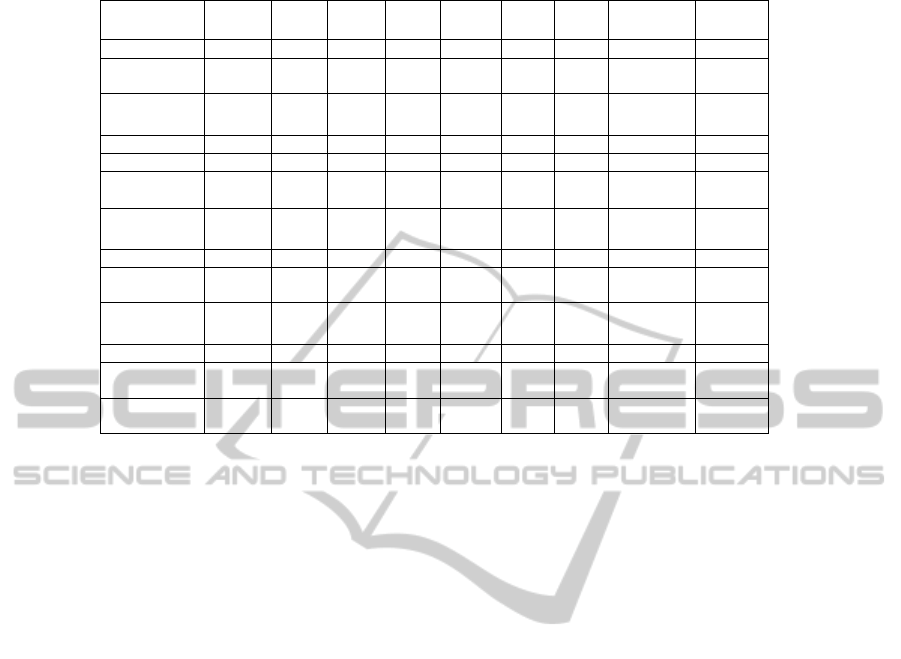
Table 4: Returns and fraction of good decisions produced by individual predictors and multivariate models.
Predictorsused Index MC Mom BtoM DO_RR DO NS
MC,BtoM,
DO_RR
MC,NS,
DO_RR
1985‐2010
FractionGood
Decisions
0.57 0.53 0.60 0.47 0.49 0.39 0.50 0.50
Annualised
Returns(%)
22.5 44.98 49.60 33.17 31.64 34.21 22.34 42.89 40.24
NormStdRet
3.96 2.97 2.35 2.51 2.84 2.82 3.85 3.08 3.10
1985‐1995
FractionGood
Decisions
0.67 0.53 0.77 0.51 0.56 0.28 0.47 0.53
Annualised
Returns(%)
27.75 95.31 59.46 69.40 51.07 46.84 13.17 57.34 71.59
1995‐2005
FractionGood
Decisions
0.60 0.54 0.53 0.44 0.47 0.38 0.61 0.51
Annualised
Returns(%)
20.93 36.74 54.73 33.72 24.75 36.22 29.61 44.43 43.29
2005‐2010
FractionGood
Decisions
0.46 0.52 0.57 0.51 0.48 0.47 0.43 0.46
Annualised
Returns(%)
21.83 28.65 33.13 9.29 31.29 21.45 16.13 26.96 9.73
over subsequent time periods when the model is
used for return prediction.
When comparing the different measures for
model quality, it is interesting to note that models or
predictors with a higher correlation coefficient
between actual and predicted share returns do not
always produce better results in terms of portfolio
returns. E.g. using MC as predictor produces a
correlation coefficient of 15.0%, an EqW relative
return of 4.3% and a ValW relative return of 2.3%.
The linear model using MC, BtoM and DO_RR has
a correlation coefficient of only 13.8% but produces
EqW and ValW relative returns of 5.0% and 3.0%,
respectively.
Another interesting aspect is the degree to which
the same predictor or model retains predictive
capabilities over all three stock categories (Micro,
Small and Big). It is clear that models including MC
as predictor do not perform well for the Big and
Small categories, while models including BtoM and
DO or DO_RR perform much better for these
categories, indicating that these predictors capture a
larger portion of cross-sectional share differences in
the Big and Small categories.
Table 4 displays the results for simulated returns
over the trading period 1985-2010, using either
individual predictors or predicted returns generated
by multivariate models to select portfolios. Results
are shown for the entire period 1985-2010, as well
as for the three periods 1985-1995, 1995-2005 and
2005-2010. In addition to the returns generated over
the respective period, the table also displays the
fraction of good decisions resulting from each stock
selection criteria.
The highest returns over an specific time period
is produced using MC as criteria, producing a return
of 95.3% for the period 1985-1995. It must be noted
that the size of the portfolio was still small during
this period – as portfolio size grew over subsequent
periods, the returns generated by MC reduced
substantially.
The multivariate models based on several
predictor variables tend to perform more
consistently over the entire time period compared to
the individual predictors contained in these models,
and, except for small portfolios (where MC performs
the best on its own) outperforms the performance of
the individual predictors used to train these models.
9 SUMMARY AND
CONCLUSIONS
The primary contribution of this paper is to show
how robust statistical analysis can be used as basis
for evaluating the ability of indicators, as well as of
models based on such indicators, to identify stocks
with above average return expectations. The
simulated trading strategy demonstrates that
employing these indicators as basis for stock
selection can lead to risk-adjusted returns that far
exceed returns associated with the market index.
The paper furthermore practically demonstrates
that conventional statistical parameters like
ICFC 2010 - International Conference on Fuzzy Computation
418

correlation coefficient are not necessarily the most
appropriate to use for selecting stocks to produce
abnormal returns. The approach introduced by Fama
and French (2008) to compile sorted categories with
associated sorted returns seem to be more suitable to
select stocks that are associated with above average
probabilities of outperforming the market.
The third important observation is that the
relatively basic approach used in this work can
produce results that compare favourably with
strategies based on extracting time series prediction
models for each individual stock. It is important to
note that the indicators and models developed in this
work are common to all stocks, whereas most other
approaches require different models for individual
stocks.
A fourth observation is that stocks from an
exchange operating within a developing economy
(the JSE representing the South African economy)
behave in much the same way as stocks listed on the
NYSE with respect to a number of fundamental and
technical indicators. MC is confirmed to be the
strongest individual indicator of abnormal returns
(although this may be explained by the higher risk
associated with smaller stocks), with BtoM
providing the best indicator of abnormal returns for
non-micro cap stocks. Between them these two
parameters seem to be useful indicators to predict
excess returns for growth and value stocks
respectively.
The exercise to develop multivariate models
using these predictors as inputs shows that, while the
best performance of the multivariate models is not
much better than the best results with individual
predictors, the multivariate models tend to be more
consistent over different time periods and for
different size categories. These models seem to be
able to use the abilities of the different indicators in
such a way that the best predictive abilities of each
is used when the others tend to loose some of their
predictive capabilities (e.g. when moving from
Micro to Big portfolios).
ACKNOWLEDGEMENTS
The author would like to acknowledge the assistance
of the School of Business Mathematics and
Informatics, including mr Thys Cronjé, at Northwest
University for providing the stock data that was used
for this work.
REFERENCES
Fama, E. F., French, K. R., August 2008. Dissecting
Anomalies. In The Journal of Finance, LXIII(4).
Altay, E., Satman, M. K., Stock market forecasting:
artificial neural network and linear regression
comparison in an emerging market, 2005. In Journal
of Financial Management and Analysis, 18(2).
Lorek, K. S. et al, 1983. Further descriptive and predictive
evidence on alternative time-series models for
quarterly earnings. In Journal of Accounting Research,
21(1).
Bekiros, S. D., 2007. A neurofuzzy model for stock
market trading. In Applied Economics Letters, Vol. 14.
Jasic, T., Wood, D. 2004. The profitability of daily stock
market indices trades based on neural network
predictions. In Applied Financial Economics, 14.
Blasco, N., Del Rio, C., Santamaria, R., The random walk
hypothesis in the Spanish stock market: 1980-1992.
June 1997. In Journal of Business Finance and
Accounting, 24(5).
Kluppelberg, C. et al, 2002. Testing for reduction to
random walk in autoregressive conditional
heteroskedasticity models. In Econometrics Journal,
5, pp. 387-416.
Fama, E. F., French, K. R., 2004. The Capital Asset
Pricing Model: Theory and Evidence. In Journal of
Economic Perspectives, 18(3).
Alcock, J., Gray, P., June 2005. Forecasting stock returns
using model-selection criteria. In The Economic
Record, 81(253).
Huang, W. et al, 2007. Neural networks in finance and
economic forecasting. In International Journal of
Information Technology and Decision Making, 6(1).
Sharpe, William F., 1964, Capital asset prices: A theory of
market equilibrium under conditions of risk, Journal
of Finance 19, 425–442.
DEVELOPING MULTIVARIATE MODELS TO PREDICT ABNORMAL STOCK RETURNS - Using Cross-sectional
Differences to Identify Stocks with Above Average Return Expectations
419
