
SOLVING THE RING ARC-LOADING PROBLEM USING
A HYBRID SCATTER SEARCH ALGORITHM
Anabela Moreira Bernardino, Eugénia Moreira Bernardino
Research Center for Informatics and Communications, Dep. of Computer Science, School of Technology and Management
Polytechnic Institute of Leiria, Leiria, Portugal
Juan Manuel Sánchez-Pérez, Juan Antonio Gómez-Pulido and Miguel Angel Vega-Rodríguez
Dep. of Technologies of Computers and Communications, Polytechnic School, University of Extremadura, Cáceres, Spain
Keywords: Communication Networks, Weighted Ring Arc-Loading Problem, Scatter Search Algorithm, Bio-inspired
Algorithms.
Abstract: Resilient Packet Ring (RPR) is a standard that uses Ethernet switching and a dual counter-rotating ring
topology to provide SONET-like network resiliency and optimised bandwidth usage, while it delivers
multipoint Ethernet/IP services. An important optimisation problem arising in this context is the Weighted
Ring Arc Loading Problem (WRALP). That is the design of a direct path for each request in a
communication network, in such a way that high load on the arcs will be avoided, where an arc is an edge
endowed with a direction. The load of an arc is defined as the total weight of those requests routed through
the arc in its direction. WRALP ask for a routing scheme such that the maximum load on the arcs will be
minimum. In this paper we study the loading problem without demand splitting and for solving it we
propose a Hybrid Scatter Search (HSS) algorithm. Coupled with the Scatter Search algorithm we use a Tabu
Search algorithm to locate the global minimum. We show that HSS is able to achieve feasible solutions to
WRALP instances, improving the results obtained by previous approaches.
1 INTRODUCTION
The past two decades have witnessed tremendous
research activities in optimisation methods for
communication networks. Resilient Packet Ring
(RPR), also known as IEEE 802.17, is a standard,
designed to optimise the transport of data traffic
through optical fiber ring networks (Davik et al.,
2004; RPR Alliance, 2004; Yuan et al., 2004). The
RPR aims to combine the appealing functionalities
of Synchronous Optical Network/Synchronous
Digital Hierarchy (SONET/SDH) networks with the
advantages of Ethernet networks. The load balancing
model for RPR differs from the SONET/SDH ring
loading. Namely, SONET/SDH demands are bi-
directional and the demands assigned to go
clockwise compete for common span capacity with
the demands assigned to go counter-clockwise. In
RPR there are two distinct rings (clockwise and
counter-clockwise) and the demands do not compete
for common capacity. In this paper we consider the
Weighted Ring Arc-Loading Problem (WRALP)
which arises in engineering and planning of RPR
systems. Specifically, for a given set of non-splitable
and unidirectional point-to-point demands, the
purpose is to find the routing for each demand so
that the maximum link segment load will be
minimised (Karunanithi and Carpenter, 1994; Cho et
al., 2005; Kim et al., 2008; Bernardino et al., 2010a).
There are three variants to solve this problem: (i)
demands can be split in two parts, and then each one
is sent in a different direction; (ii) demands are
allowed to be split in two parts, but restricted to be
integrally split; (iii) each demand must be entirely
routed in either one of the two directions, clockwise
or counter-clockwise. In this paper we study the
third variant, where NP-hardness can be drawn from
the results in literature (Cosares and Saniee, 1994;
Kubat and Smith, 2005).
Cosares and Saniee (1994) and Dell’Amico et al.
(1998) studied a similar no-split loading problem on
60
Moreira Bernardino A., Moreira Bernardino E., Manuel Sánchez-Pérez J., Antonio Gómez-Pulido J. and Angel Vega-Rodríguez M..
SOLVING THE RING ARC-LOADING PROBLEM USING A HYBRID SCATTER SEARCH ALGORITHM.
DOI: 10.5220/0003076200600069
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 60-69
ISBN: 978-989-8425-31-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

SONET/SDH rings. For the split problem, several
approaches have been summarised by Schrijver et al.
(1998) and their algorithms are compared in Myung
and Kim (2004) and Wang (2005). Recently Kim et
al. (2008) presented an Ant Colony Optimisation
(ACO) algorithm using different strategies to solve
the loading problem on SONET/SDH rings.
The non-split WRALP considered in the present
paper is identical to the one described by Kubat and
Smith (2005) (non-split WRALP), Cho et al. (2005)
(non-split WRALP and split WRALP) and Yuan and
Zhou (2004) (split WRALP), that studied the
loading problem on RPR systems .
We verify that the main purpose of previous
works was to build feasible solutions for the loading
problems in a reduced amount of time. Our purpose
is different - we want to compare the performance of
our algorithm with others in the achievement of the
best-known solution. Using the same principle
Bernardino et al. (2008, 2009a, 2009b, 2010a,
2010b) presented several Evolutionary Algorithms
(EAs) and a Tabu Search (TS) algorithm to solve the
non-split loading problem on SONET/SDH rings
and several EAs and Swarm Optimisation
algorithms to solve the non-split WRALP.
The WRALP problem is a NP-complete
combinatorial optimisation problem (Cosares and
Saniee, 1994; Kubat and Smith, 2005). It means that
we cannot guarantee to find the best solution in a
reasonable amount of time. In practice, approximate
methods are used to find a good solution to complex
combinatorial optimisation problems where classical
heuristics have failed to be efficient. The existing,
successful methods in approximate optimisation fall
into two classes: Local Search (LS) and population-
based search. There are many LS and population-
based optimisation algorithms.
This paper presents an application of a
population-based optimisation algorithm called the
Scatter Search (SS) algorithm combined with a LS
technique called the Tabu Search (TS).
The SS is an EA that has recently been found to
be promising to solve combinatorial optimisation
problems. The SS was first introduced in 1977 by
Fred Glover and extensive contributions have been
made by Manuel Laguna (2002). The SS operates on
a small set of solutions and makes only limited use
of randomisation as a proxy for diversification when
searching for an optimal solution.
Embedded in the SS algorithm we use a TS
algorithm, which is used to improve the solutions’
quality. The TS algorithm is a mathematical
optimisation method, which belongs to the class of
LS techniques.
We compare the performance of Hybrid SS
(HSS) algorithm with five algorithms: Probability
Binary Particle Swarm Optimisation (PBPSO),
Genetic Algorithm (GA), Hybrid Differential
Evolution (HDE) algorithm, Hybrid ACO (HACO)
algorithm and Discrete Differential Evolution
(DDE), used in literature.
The paper is structured as follows: in Section 2
we present the problem definition; in Section 3 we
describe the implemented HSS algorithm; in Section
4 we discuss the computational results obtained and
in Section 5 we report about the conclusions.
2 PROBLEM DEFINITION
An optimal loading balance in RPR systems is of
paramount importance as it increases system
capacity and improves the overall ring performance.
Considering a given set of non-split and
unidirectional point-to-point requests (weights), the
purpose is to find the routing for each request in
such a way that the maximum arc load will be
minimised (Schrijver et al., 1998).
Let R
n
be a n-node bidirectional RPR ring with
nodes {n
1
,n
2
,…,n
n
} labelled clockwise. Each
edge {e
k
,e
k+1
} of R
n
, 1≤ k ≤ n, is taken as two
arcs with opposite directions, in which the data
streams can be transmitted in either direction:
)
1kkk
e,(ea
+
+
=
or )e,(ea
k1kk +
−
= .
A communication request on R
n
is an ordered pair
(s,d) of distinct nodes, where s is the source and
d is the destination. We assume that data can be
transmitted clockwise or counter-clockwise on the
ring, without splitting. We use P
+
(s,d) to denote
the directed (s,d) path clockwise around R
n,
and
P
-
(s,d) the directed (s,d) path counter-
clockwise around R
n
.
Often a request (s,d) is associated with an
integer weight w>=0; we denote this weighted
request by (s,d;w). Let Z={(s
1
,d
1
;w
1
),
(s
2
,d
2
;w
2
),...,(s
m
,d
m
;w
m
)} be a set of
integrally weighted requests on R
n
. For each request
(s
i
,d
i
) we need to design a directed path P
i
of R
n
from s
i
to d
i
. A collection P={P
i
: i=1,2,…,m}
of such directed paths is called a routing for Z.
In this work, the solutions are represented using
binary vectors (Table 1). If a position has the value
1 the demand flows in the clockwise direction, if it
has the value 0, it flows in the other way.
We assume that weights cannot be split, that is,
for some integer L
i
=1, 1≤ i ≤ m, the total amount
of data is transmitted along P
+
(s
i
,d
i
); L
i
=0, the
SOLVING THE RING ARC-LOADING PROBLEM USING A HYBRID SCATTER SEARCH ALGORITHM
61

total amount of data is transmitted along P
-
(s
i
,d
i
). The vector L= (L
1
,L
2
,…,L
m
)determines
a routing scheme for Z.
Table 1: Representation of the solution.
Pair(s, t) Demand
1: (1, 2) Æ 15
2: (1, 3) Æ 3
3: (1, 4) Æ 6
4: (2, 3) Æ 15
5: (2, 4) Æ 6
6: (3, 4) Æ 14
n=numberNodes=4
m=numberPairs=6
15 C
3 CC
6 CC
15 C
6 CC
14 C
C - clockwise
CC - counter clockwise
Representation (x)
Pair
1
Pair
2
Pair
3
Pair
4
Pair
5
Pair
6
1 0 0 1 0 1
3 SCATTER SEARCH
ALGORITHM
This metaheuristic technique derives from strategies
proposed by Glover (1977) to combine decision
rules and constraints, and was successfully applied
to a large set of problems (Glover et al., 2003). The
basic idea is to create a set of solutions (the
reference set), that guarantees a certain level of
quality and diversity. The iterative process consists
in selecting a subset of the reference set, combining
the corresponding solutions through a strategy, in
order to create new solutions and to improve them
through a LS optimisation technique. The process is
repeated with the use of diversification techniques,
until certain stopping criteria are met.
In SS algorithm it is built an initial set of
solutions (reference set) and then the elements of
specific subsets of that set are systematically
combined to produce new solutions, which hopefully
will improve the best-known solution (see Glover et
al., 2003 for a comprehensive description of the
algorithm).
The basic algorithmic scheme is composed of
five steps:
1. Generation and improvement of solutions;
2. Construction of the reference set;
3. Subset selection;
4. Combination;
5. Reference set update.
The standard SS algorithm stops when the reference
set cannot be updated. However, the scheme can be
enhanced by adding new steps in which the
reference set is regenerated. Our algorithm uses a
diversification mechanism after a pre-defined
number of nid iterations without improving the best
solution found so far. The reinitialisation can be very
useful to refocus the search on a different search
space region and to avoid the early convergence of
the algorithm.
The main steps of the HSS algorithm applied to
the WRALP are detailed below:
Initialise Parameters
Generate initial set of Solutions
Evaluate Solutions
Apply Improvement Method
Generate Reference Set
WHILE TerminationCriterion()
Select subsets
Apply Combination Method
Apply Improvement Method
Update Reference Set
IF (no new solutions) THEN
Regenerate Reference Set
IF (nid iterations without improve
best solution) THEN
Apply Diversification Mechanism
The next subsections describe each step of the
algorithm in detail.
3.1 Initialisation Parameters
The following parameters, must be defined by the
user: (1) mi– number of iterations; (2) ni– number
of initial solutions; (3) b1– number of best solutions
in the reference set; (4) b2– number of most
different feasible solutions in the reference set and
(5) nid- number of iterations without improvement
(used for diversification).
3.2 Generation of Solutions
The initial solutions can be randomly created or in a
deterministic form based in a Shortest-Path
Algorithm (SPA). The SPA is a simple traffic
demand assignment rule in which the demand will
traverse the smallest number of segments.
3.3 Evaluation of Solutions
To evaluate how good a potential solution is relative
to other potential solutions we use a fitness function.
The fitness function returns a positive value (fitness
value) that reflects how optimal the solution is.
The fitness function is based on the fitness
function used in (Bernardino et al., 2008, 2009a,
2009b, 2010a, 2010b ):
W
i
,…,w
m
between(s
i
,d
i
),…,(s
m
,d
m
) (1a)
L
i
, …, L
m
= 0 Æ P
-
(s
i
,d
i
)
ICEC 2010 - International Conference on Evolutionary Computation
62

1 Æ P
+
(s
i
,d
i
) (1b)
Load on arcs:
Load(L,
+
k
a
)=
∑
++
∈ )d,(sPa:i
i
iik
w
(2a)
Load(L,
−
k
a
)=
∑
−−
∈ )d,(sPa:i
i
iik
w
(2b)
∀k=1,…,n; ∀i=1,…,m
Fitness function:
max {max Load(L,
+
k
a
),
max Load(L,
−
k
a
)} (3)
For a given ring, between each node pair (s
i
,t
i
)
there is a demand value >=0. Constraint sets (1)
state that each positive demand value is routed in
either clockwise (C) or counter-clockwise (CC)
direction.
For an arc, the load is the sum of w
i
for
clockwise or counter-clockwise between nodes e
k
and e
k+1
(2). The purpose is to minimise the
maximum load on the arcs of a ring (3).
3.4 Generation of Reference Set
The best b1 solutions in the initial set of solutions
are selected to be in the reference set. The b2
feasible solutions in the initial set of solutions that
are the most different when compared to the
solutions already in the reference set, are also
selected to be in the reference set.
As a measure of the difference between two
solutions, we compute the total number of different
assignments between the two solutions.
3.5 Subset Selection
In literature, several methods can be applied to
generate the subsets. In our implementation, the
subsets are formed by combining two solutions from
the reference set:
(1,2), (1,3), (1,4),…, (1,b1+b2),
(2,3),…, (b1+b2-1,b1+b2).
We adopt Type-1 (Glover et al., 2003). This
method consists of ((b1+b2)
2
- (b1+b2))/2
pair wise combinations of the solutions.
All pairs of solutions in the reference set are
selected for the combination procedure (see
subsection 3.6).
3.6 Combination Method
This method combines the solutions in each subset
to form new solutions.
First a random node is chosen and then the pairs
with that node are exchanged (see Fig. 1) between
the two solutions.
Figure 1: .Combination Method – produces two combined
solutions – example with n=4 (number of nodes) and m=6
(number of pairs). The node chosen was “1”.
The combination method consists of the
following steps:
node= random(n)
FOR i=1 TO m DO
IF Solution1(i) has node OR
Solution2(i) has node THEN
CombinedSolution1(i)= Solution2(i)
CombinedSolution2(i)= Solution1(i)
ELSE
CombinedSolution1(i)= Solution1(i)
CombinedSolution2(i)= Solution2(i)
The combination method produces two combined
solutions.
The combined solutions go through the
improvement phase (see subsection 3.7).
3.7 Improvement Method
A TS algorithm is applied to each solution in the
initial set of solutions in order to reduce its cost, if
possible. After the combination, the TS algorithm is
also applied to improve the quality of the combined
solutions.
The basic concept of TS was described by
Glover (1986). TS allows the search to explore
solutions that decrease the objective function value
only in those cases where these solutions are not
forbidden. This is usually obtained by keeping track
of the action used to transform one solution into the
next. When an action is performed it is considered
tabu for the next T iterations, where T is the tabu
status length. A solution is forbidden if it is obtained
SOLVING THE RING ARC-LOADING PROBLEM USING A HYBRID SCATTER SEARCH ALGORITHM
63

by applying a tabu action to the current solution.
In our implementation, the TS only exploits a
part of the neighbourhood. The most common and
simplest way to generate a neighbour is to exchange
the direction of the traffic of one request. In our
implementation, some positions of the solution are
selected and their directions are exchanged (partial
search). This method can be summarised in the
following pseudo-code steps:
p1 = random (m)
p2 = random (m)
N = neighbourhoods of ACTUAL-
SOLUTION (one neighbourhood results of
interchange the direction of p1 and/or
p2)
SOLUTION = FindBest (N)
If ACTUAL-SOLUTION is worst than
SOLUTION
ACTUAL-SOLUTION = SOLUTION
The positions which directions are exchanged are
classified as tabu attributes. A candidate can be
chosen as a new current solution, if the positions
which directions are exchanged are not the same as
those in the tabu list. Normally in TS algorithm, if a
neighbour is the best solution found so far it could
be selected as a move, even when it is tabu. In our
implementation, we don’t explore neighbours when
the two pairs chosen are in the tabu list. In
aspiration, just the best neighbour not tabu with a
fitness value lower than the best is selected.
The TS ends when a maximum number of
iterations is reached. Based on preliminary
observations, we consider a maximum number of 10
iterations. With a higher value of iterations, the
algorithm slows down. We also observed that a high
number of iterations does not produce significant
better results.
For the tabu list, we consider m/20 elements. In
the tests carried out with TS, it was verified that the
number of elements in the tabu list does not have a
significant influence on the efficiency and quality of
the search. However, if the number of elements is
high, the search space will be small, which may lead
to a premature convergence of the algorithm. On the
other hand, if the number of elements is small, the
search space will be large, which may take a long
time to obtain a good solution.
The improved solutions are considered for
inclusion in the reference set (see subsection 3.8).
3.8 Reference Set Update
The purpose is to maintain a good level of quality
and diversity.
We adopted the dynamic reference set update
(Glover et al., 2003).
A new feasible solution immediately enters in
the reference set, if its quality is better than the
quality of the worst solution, or if its diversity is
greater than the diversity of the less different
solution. Solutions that are equal to others already in
the reference set are not allowed to enter under any
condition.
If the reference set is not updated, then the
algorithm restarts the reference set (see subsection
3.9).
3.9 Regeneration of Reference Set
The algorithm creates another set of solutions - Ps
(with the same size of the initial set of solutions).
The new solutions go through the improvement
phase (see subsection 3.7).
A new feasible solution immediately enters in
the reference set, if its quality is better than the
quality of the worst solution.
The b2 solutions with greater diversity are
erased from the reference set and the b2 feasible
solutions in Ps that are the most different when
compared to the solutions already in the reference
set are selected to be in the reference set.
3.10 Diversification Mechanism
This mechanism restarts the best b1 solutions in the
reference set.
The algorithm creates another set of solutions -
Pd (with the same size of the initial set of solutions).
The new solutions go through the improvement
phase (see subsection 3.7).
The best (b1-1) solutions in Pd are selected to
be in the reference set. For the following iteration,
we kept the best solution.
3.11 Termination Criterion
The algorithm stops when a maximum number of
iterations (mi) is reached.
4 RESULTS
We evaluate the utility of the algorithms using the
ICEC 2010 - International Conference on Evolutionary Computation
64

same instances produced by Bernardino et al.
(2009a, 2009b, 2010a, 2010b). The studied
examples arise by considering six different ring sizes
– 5, 10, 15, 20, 25 or 30 nodes. A ring in a
telecommunication network will typically contain
between 5 and 20 nodes. The instances consider the
5, 10 and 15 node rings to be ordinary-sized rings
and the 20, 25 and 30 node rings to be extremely
large rings. The demand cases are:
Case 1: complete set of demands between
5 and 100 with uniform distribution;
Case 2: half of the demands in Case 1 set
to zero;
Case 3: 75% of the demands in Case 1 set
to zero.
Case 4: complete set of demand between 1
and 500 with uniform distribution. This case was
only used for the 30 nodes ring.
It was generated 1 different problem instance for
each case. This yields 3 instances for each ring size
(4 instances for the 30 nodes ring). For
convenience, they are labelled C
ij
, where 1<i<6
represents the ring size and 1<j<4 represents the
demand case.
Figure 2: Number of initial solutions – Average
Fitness/Execution Time/Number of Best-known Solutions
- b1 =[4,8], b2=[4,8] and nid= [m/10, m/2] .
Figure 3: Number of best solutions in the reference set
(parameter b1) – Average Fitness/Execution Time/
Number of Best-known Solutions – ni=10.
We perform comparisons between all parameters
(using all instances) in order to establish the correct
parameter setting for the HSS algorithm.
We consider the same instance – C41 (a problem
with average difficulty) to show the comparisons
between parameters. To compute the results we use
50 iterations.
The best results obtained with the HSS algorithm
use ni between 40 and 100, b1 between 4 and 10,
b2 between 4 and 10 and nid between m/10 and
m/2. These parameters were experimentally
considered good and robust for the problems tested.
The number of initial solutions was set to {10,
20, 30, 40, 50, 60, 70, 80, …, 200}. We studied
the impact on the execution time, the average fitness
and the number of best-known solutions found. The
number of solutions has a significant impact on the
execution time (see Figure 2).
The best results obtained with HSS use ni
between 40 and 100. With these values, the
algorithm can reach, in a reasonable amount of time,
a reasonable number of best-known solutions (see
Figure 2). With a higher number of solutions, the
algorithm is more time consuming.
The number of solutions in the reference set is
typically small - 20 solutions or less (Glover et al.,
2003). In our experiments the number of solutions
b1 and the number of solutions b2 were set to {1,
SOLVING THE RING ARC-LOADING PROBLEM USING A HYBRID SCATTER SEARCH ALGORITHM
65

2, 3, 4, 5, 6, 7, 8, 9, 10}. We studied
the impact on the execution time, the average fitness
and the number of best-known solutions found. The
number of solutions in the reference set has a
significant impact on the execution time (see Figure
3 and Figure 4).
Figure 4: Number of most different feasible solutions in
the Reference Set (parameter b2) – Average
Fitness/Execution Time/Number of Best-known Solutions
– ni=10.
The results show that the best results obtained use
b1>=4 and b2>=4 (see Figure 3 and Figure 4).
These parameters were experimentally found to be
good and robust for the problems tested. With
b1+b2>20 the algorithm can reach a better average
fitness but it is more time consuming.
We observe that a small number of solutions in
the reference set allows an initial faster convergence,
but a worse final result, following to an increased
amount of suboptimal values. This can be explained,
because the quality of the initial best-located
solution previous to the first restart highly depends
on the reference set size: they need more diversity to
avoid premature stagnation.
For parameter nid, the number of iterations
used for diversification, the values between m/10
and m/2 have been shown to be experimentally
more efficient.
Phenomena of stagnation and insufficient
intensification have been observed for values of nid
lesser than m/10 and greater than m/2.
In general, the experiments have shown that the
proposed parameter setting is very robust to small
modifications.
In this paper, we only compare our algorithm
with: PBPSO (Bernardino et al., 2009a), GA
(Bernardino et al., 2008), HDE (Bernardino et al.,
2009b), HACO (Bernardino et al., 2010a) and DDE
(Bernardino et al., 2010b) because the authors: (1)
use the same test instances; (2) adopt the same
fitness function; (3) implement the algorithms using
the same language (C++) and; (4) adopt the same
representation (binary).
Suggestions from literature helped us to guide
our choice of parameter values for PBPSO, GA
HDE, HACO and DDE (Bernardino et al., 2008,
2009a, 2009b, 2010a, 2010b).
PBPSO was applied to populations of 40
particles and we consider the value 1.49 for the
parameters C1 and C2, and for the inertia velocity
(W) values in the range [0.6,0.8].
GA was applied to populations of 200
individuals; it uses “Uniform” as recombination
method, “Multiple” as mutation method and
“Tournament” as selection method. For GA, we
consider crossover probability in the range
[0.6,0.9] and mutation probability in the range
[0.5,0.7].
HDE was applied to populations of 50
individuals, it uses the “Best1Bin” strategy, CR in
the range [0.3,0.5] and factor F in the range
[0.5,0.7].
For the HACO, we consider populations of 40
individuals, 30 modifications, Q=100, x1 in the
range
[0.6,0.8], x2 in the range [0.7,0.8]
and q in the range [0.7,0.8].
For the DDE, we consider populations of 50
individuals, 5 perturbations, pc in the range
[0.1,0.2], pp in the range [0.6,0.8] and the
LS method “Exchange Direction”.
Finally, the parameters of the HSS algorithm
were set to ni=50, b1 between 4 and 8, b2
between 4 and 8, number of iterations of the TS =3
and nid between m/10 and m/2. The six
algorithms were executed using a processor Intel
Quad Core Q9450. The initial solutions of the six
algorithms were created using random solutions. For
the instance C64 the SPA was used to create the
ICEC 2010 - International Conference on Evolutionary Computation
66

Table 2: Best obtained results.
Instance Nodes Pairs Best Fitness Iterations
C11
5 10
161 25
C12
5 8
116 10
C13
5 6
116 10
C21
10 45
525 50
C22
10 23
243 25
C23
10 12
141 10
C31
15 105
1574 100
C32 15 50 941 50
C33 15 25 563 25
C41 20 190 2581 300
C42 20 93 1482 100
C43 20 40 612 50
C51 25 300 4265 500
C52 25 150 2323 400
C53 25 61 912 250
C61 30 435 5762 1500
C62 30 201 2696 1000
C63 30 92 1453 500
C64 30 435 27779 500
Table 3: WRALP results – run times and number of iterations.
Inst.
PBPSO GA HDE HACO DDE HSS
Time IT Time IT Time IT Time IT Time IT Time IT
C11 <0.001 2 <0.001 2
<0.001 2 <0.001
2
<0.001 2
<0.001 2
C12 <0.001 2 <0.001 2
<0.001 2 <0.001
2
<0.001 2
<0.001 2
C13 <0.001 1 <0.001 1
<0.001 1 <0.001
1
<0.001 1
<0.001 1
C21 <0.001 15 <0.001 15
<0.001
10
<0.001
20
<0.001
10
<0.001 10
C22 <0.001 3 <0.001 5
<0.001 3 <0.001
3
<0.001 3
<0.001 3
C23 <0.001 3 <0.001 3
<0.001 3 <0.001
3
<0.001 3
<0.001 3
C31 0. 1 20 0. 1 30
0. 1
15
0. 1 30
0. 1
10
0. 1 10
C32 <0.001 8 <0.001 15
<0.001
5
<0.001
10
<0.001
5
<0.001 5
C33 <0.001 5 <0.001 5
<0.001
5
<0.001
5
<0.001
3
<0.001 3
C41 0.2 50 0.1 50
0.1 30
0.15 50
0.1 25
0.1 20
C42 0.075 20 0.075 40
0.05 10
0.06 25
0.05 8
0.05 10
C43 <0.001 5 <0.001 10
<0.001
5
<0.001 5
<0.001
3
<0.001 5
C51 0.75 80 0.75 80
0.75 40
0.6 100
0.5 30
0.5 30
C52 0.1 25 0.1 40
0.1 15
0.1 30
0.1 15
0.1 15
C53 0.01 15 0.01 25
0.01 10
0.01 20
0.01 8
0.01 10
C61 2 130 1.75 130
1.75 40
1.75 150
1.5 50
1.3 40
C62 0.4 50 0.2 60
0.25 20
0.4 60
0.25 25
0.25 20
C63 0.075 15 0.075 30
0.075 10
0.075 20
0.06 10
0.05 10
C64 0.5 40 0.3 30
0.25 5
0.5 5
0.1 3
0.1 5
Table 4: WRALP results – Average Fitness / Average Time / Standard Deviation.
Inst It PBPSO GA HDE HACO DDE HSS
AF AT SD AF AT SD AF AT SD AF AT SD AF AT SD AF AT SD
C41 50 2594,36 0,26 7,70 2587,62 0,17 3,46 2584,31 0,27 1,15 2591,23 0,16 7,73 2582,06 0,16 1,18 2581,50 0,22 0,71
C51 75 4291,52 0,86 16,85 4273,18 0,43 2,97 4271,27 0,7 5,10 4279,49 0,76 10,10 4268,96 0,53 5,71 4265,68 0,65 1,16
C61 100 5837,58 3,10 23,19 5784,62 1,34 10,05 5783,18 1,87 7,45 5793,68 2,23 14,17 5781,52 1,39 9,78 5763,72 1,44 2,25
SOLVING THE RING ARC-LOADING PROBLEM USING A HYBRID SCATTER SEARCH ALGORITHM
67
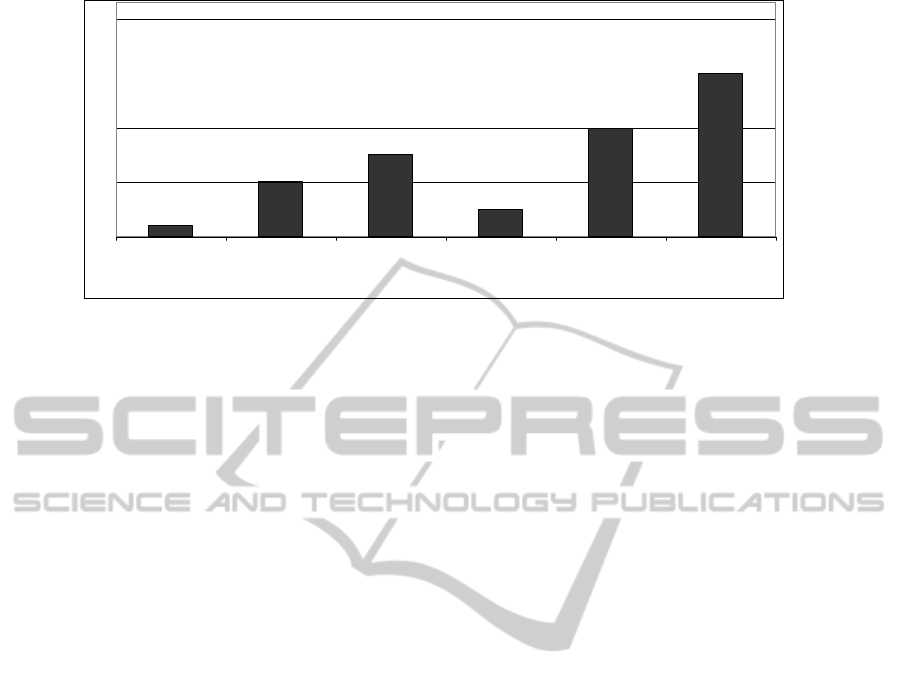
PBPSO GA HDE HA CO DDE HSS
Algorithms
Percentage of best solutions
Figure 5: Percentage of best-known solutions obtained by the six algorithms – instance C41 (50 iterations).
initial populations. Table 2 presents the best
obtained results. The first column represents the
instance number (Instance), the second and third
columns show the nodes’ number (Nodes) and the
pairs’ number (Pairs), the fourth column
demonstrates the minimum fitness values obtained
and the fifth column demonstrates the number of
iterations used to test each instance. The number of
iterations was selected based upon preliminary
observations.
Table 3 presents the best WRALP results
obtained with the six implemented algorithms. The
first column represents the instance number (Inst.)
and the remaining columns demonstrate the obtained
results (Time – Run Times, IT – Iterations) by the
six algorithms. The presented values have been
computed based on 100 different executions for
each test instance, using the best combination of
parameters found and different seeds. Table 4 only
considers the 30 best executions. The six algorithms
reach feasible solutions for all test instances and all
the algorithms reach the best-known solutions before
the run times and the number of iterations presented.
In comparison, the HSS algorithm produces a
higher number of best-known solutions using the
same number of iterations (Figure 5). The DDE
algorithm obtains a reasonable number of best-
known solutions and a good average fitness in a
better running time (Figure 5, Table 4). The PBPSO
is the slowest algorithm and it obtains a smaller
number of best-known solutions comparing with the
other algorithms (Figure 5).
When using the SPA to create the initial
solutions, the times and number of iterations
decrease – instance C64. This instance is
computationally harder than the C61 however the
best-known solution is obtained faster. Based on
preliminary observations we consider more efficient
to initially apply a SPA and after, a metaheuristic to
improve the solutions.
Table 4 presents the WRALP average fitness and
the WRALP average time obtained with PBPSO,
GA, HDE, HACO and DDE using a limited number
of iterations for the instances C41, C51 and C61
(harder instances). The first column represents the
instance number (Instance), the second column
demonstrates the number of iterations used to test
each instance and the remaining columns show the
obtained results (AF – Average Fitness, AT –
Average Time, ST – Standard Deviation) by the six
algorithms. The results have been computed based
on 100 different executions for each test instance
using the best combination of parameters found and
different seeds.
As it can be seen, the average fitness and
standard deviations for the HSS are smaller. It
means that the HSS is more robust than the other
algorithms. DDE also presents a good average
fitness and a good standard deviation.
5 CONCLUSIONS
In this paper we present a Hybrid Scatter Search
algorithm to solve the WRALP. The Hybrid Scatter
Search Algorithm is an evolutionary optimisation
technique, able to perform simultaneous local and
global search.
The performance of' Hybrid Scatter Search
algorithm is compared with five algorithms from
literature, namely: PBPSO, GA, HDE, HACO and
DDE.
Relatively to the problem studied, the Hybrid
Scatter Search algorithm presents better results. The
computational results show that it had a stronger
performance, improving the results obtained by
previous approaches. Moreover, in terms of standard
ICEC 2010 - International Conference on Evolutionary Computation
68

deviation, the algorithm also proved to be more
stable and robust than the other algorithms.
Experimental results demonstrate that the
proposed algorithm is an effective and competitive
approach in composing satisfactory results with
respect to solution quality and execution time for the
WRALP.
In literature the application of Scatter Search
algorithm for this problem is nonexistent. For that
reason, this article shows its enforceability in the
resolution of this problem.
The continuation of this work will be the search
and implementation of new methods to speed up the
optimisation process.
REFERENCES
Bernardino, A.M., Bernardino, E.M., Sánchez-Pérez, J.M.,
Vega-Rodríguez, M.A., Gómez-Pulido, J.A., 2008.
Solving the Ring Loading Problem using Genetic
Algorithms with intelligent multiple operators. In
Proceedings of International Symposium on
Distributed Computing and Artificial Intelligence
2008 (DCAI 2008), pp. 235-244. Springer Berlin /
Heidelberg.
Bernardino, A.M., Bernardino, E.M., Sánchez-Pérez, J.M.,
Vega-Rodríguez, M.A., Gómez-Pulido, J.A., 2009a.
Solving the non-split weighted ring arc-loading
problem in a Resilient Packet Ring using Particle
Swarm Optimisation. In Proceedings of the
International Joint Conference on Computational
Intelligence, pp. 144-151. INSTICC Press.
Bernardino, A.M., Bernardino, E.M., Sánchez-Pérez, J.M.,
Vega-Rodríguez, M.A., Gómez-Pulido, J.A., 2009b.
Solving the weighted ring edge-loading problem
without demand splitting using a Hybrid Differential
Evolution Algorithm. In The 34th IEEE Conference on
Local Computer Networks, pp. 562-568. IEEE Press.
Bernardino, A.M., Bernardino, E.M., Sánchez-Pérez, J.M.,
Vega-Rodríguez, M.A., Gómez-Pulido, J.A., 2010a. A
Hybrid Ant Colony Optimization Algorithm for
Solving the Ring Arc-Loading Problem. In Artificial
Intelligence: Theories, Models and Applications, 6th
Hellenic Conference on AI, SETN 2010, 2010, pp. 49-
59. Springer Berlin / Heidelberg.
Bernardino, A.M., Bernardino, E.M., Sánchez-Pérez, J.M.,
Vega-Rodríguez, M.A., Gómez-Pulido, J.A., 2010b.
A Discrete Differential Evolution Algorithm for
solving the Weighted Ring Arc Loading Problem. In
The 23rd International Conference on Industrial,
Engineering & Other Applications of Applied
Intelligent Systems Applications of Evolutionary
Computation, pp. 61-70, Springer Berlin / Heidelberg.
Cho, K.S., Joo, U.G., Lee, H.S., Kim, B.T., Lee, W.D.,
2005. Efficient Load Balancing Algorithms for a
Resilient Packet Ring. ETRI Journal, vol.27, no.1, pp.
110-113.
Cosares, S., Saniee, I., 1994. An optimization problem
related to balancing loads on SONET rings.
Telecommunication Systems, vol. 3, no. 2, pp. 165-
181. Springer Netherlands.
Davik, F., Yilmaz, M., Gjessing, S., Uzun, N., 2004.
IEEE 802.17 Resilient Packet Ring Tutorial, IEEE
Communications Magazine, vol.42, no.3, pp. 112–118.
Dell'Amico, M., Labbé, M., Maffioli, F., 1999. Exact
solution of the SONET Ring Loading Problem.
Operations Research Letters. vol.25, no.3, pp. 119-
129.
Glover, F., 1977. Heuristics for integer programming
using surrogate constraints. Decision Sciences, vol.8,
pp. 156–166.
Glover, F., 1986. Future paths for Integer Programming
and Links to Artificial Intelligence. Computers and
Operations Research, vol. 13, no. 5, pp. 533–549.
Glover, F., Laguna, M., 1997. Tabu Search. Kluwer
Academic Publishers.
Glover, F., Laguna, M., Marti, R., 2003. Scatter Search
and Path Relinking: Advances and Applications. In
Handbook of Metaheuristics, vol. 57, pp. 1–35.
Springer.
Karunanithi, N., Carpenter, T., 1994. A Ring Loading
Application of Genetic Algorithms. In Proceedings of
the ACM Symposium on Applied Computing,
pp. 227-
231.
Kim, S.-S., Kim, I.-H., Mani, V., Kim, H.J., 2008. Ant
Colony Optimization for SONET Ring Loading
Problem. International Journal of Innovative
Computing, Information and Control, vol.4, no.7, pp.
1617-1626.
Kubat, P., Smith, J.M., 2005. Balancing traffic flows in
resilient packet rings. Girard, André (ed.) et al.,
Performance evaluation and planning methods for the
next generation internet. GERAD 25th Anniversary,
Series 6, pp. 125-140. Springer.
Laguna, M., 2002. Scatter search. In Handbook of Applied
Optimization, P. M. Pardalos and M. G. C. Resende,
editors, pp. 183–193.
Myung, Y.S., Kim, H.G., 2004. On the ring loading
problem with demand splitting. Operations Research
Letters, vol. 32, no. 2, pp. 167-173.
RPR Alliance, 2004. A Summary and Overview of the
IEEE 802.17 Resilient Packet Ring Standard.
Schrijver, A., Seymour, P., Winkler, P., 1998. The ring
loading problem. SIAM Journal of Discrete
Mathematics, vol. 11, pp. 1–14.
Wang, B.F., 2005. Linear time algorithms for the ring
loading problem with demand splitting. Journal of
Algorithms, vol. 54, no. 1, pp. 45-57.
Yuan J., Zhou S., 2004. Polynomial Time Solvability Of
The Weighted Ring Arc-Loading Problem With
Integer Splitting. Journal of Interconnection Networks,
vol. 5, no.2 , pp. 193-200.
Yuan, P., Gambiroza, V., Knightly, E., 2004 The IEEE
802.17 Media Access Protocol for High-Speed
Metropolitan-Area Resilient Packet Rings, IEEE
Network, vol.18, no.3, pp. 8–15.
SOLVING THE RING ARC-LOADING PROBLEM USING A HYBRID SCATTER SEARCH ALGORITHM
69
