
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE
Megan Katsumi and Michael Gr¨uninger
Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, Ontario, Canada
Keywords:
Ontology design, Verification, Theorem proving, First-order logic.
Abstract:
In this paper we present a methodology for the verification of first-order logic ontologies, and provide a
lifecycle in which it may be implemented to develop a correct ontology. We discuss the need for a methodology
to address development issues and illustrate the way in which this characterization of the ontology lifecycle
supports the design and deployment of ontologies within software applications. Theorem proving plays a
critical role in the specification of requirements, design, and verification of the ontology. We illustrate the
application of theorem proving in the lifecycle using examples from the PSL Ontology.
1 INTRODUCTION
The design of ontologies is a complicated process,
and there has been much work in the literature de-
voted to the development of methodologies to assist
the ontology engineer in this respect. In this paper
we present an approach to the semiautomatic verifi-
cation of first-order logic ontologies, and describe a
lifecycle in which it may be implemented to develop
a correct ontology. Our objective is not to propose
a new ontology development methodology, but rather
to use theorem proving as the basis for formally defin-
ing the steps within our methodology and their rela-
tionships to a notion of verification that focuses on
the model-theoretic properties of the ontology. Al-
though the ontology lifecycle described in this paper
was developed to address issues that arise as a result
of the semidecidable nature of first-order logic, the
methodology and lifecycle is applicable to automated
reasoning with less expressive languages.
We will discuss some existing methodologies for
ontology development, and provide motivation for the
methodology presented here. This work is a result of
experiences in the development of an extension of the
PSL ontology (Bock and Gr¨uninger, 2004; Gr¨uninger,
2009b) that is sufficient to represent flow modelling
notations such as UML, BPMN, and IDEF3. We
therefore provide a brief overview of the PSL ontol-
ogy, which will provide context for the examples of
the ontology lifecycle. The focus of the paper will be
a discussion of the role that theorem proving plays in
each phase of the lifecycle, with an emphasis on prag-
matic guidance for the semiautomatic verification of
ontologies.
2 ONTOLOGY DEVELOPMENT
IN LITERATURE
High-level methodologies for ontology development
tend to cover the breadth of the development process,
however they do not provide techniques at the more
detailed level. The On-To-Knowledge Management
(OTKM) (Sure et al., 2003) methodology covers the
full lifecycle of ontology development. It provides
useful insights into the steps required both pre- and
post- application, but it does not provide exact details
on how activities like testing should be performed, or
what is to be done if an ontology fails to satisfy a
requirement. METHONTOLOGY (Fern´andez et al.,
1997) covers areas of the lifecycle similar to what is
presented in the OTKM methodology, with a focus
on the explanation of the concepts at each stage in de-
velopment. DILIGENT (Pinto et al., 2003) provides
guidance to support the distributed (geographically or
organizationally) development of ontologies; in par-
ticular, the authors present a method to enable the
adaptation of an ontology from different parties.
Low-level ontology design methodologiesprovide
detailed instruction, concentrating on means to ac-
complish some necessary step in ontology develop-
ment. The methodology that was used in the de-
sign of the TOVE Ontology for enterprise modelling
(Gr¨uninger and Fox, 1995) introduced the notion of
competency questions to define the requirements of
an ontology and to guide the formal definition of a
set of axioms for the ontology. The Enterprise On-
tology (Uschold and King, 1995), also arising from
work with enterprise ontologies, presents an approach
37
Katsumi M. and Grüninger M..
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE.
DOI: 10.5220/0003076400370049
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 37-49
ISBN: 978-989-8425-29-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

for ontology capture that emphasizes the notion of
“middle-out” design, givingequal weight to top-down
issues (such as requirements) and bottom-up issues
(such as reuse).
The evaluation of an ontology is generally ac-
cepted as a key process in its development. The
main efforts in this area focus on taxonomy evalua-
tion (G´omez-P´erez et al., 2004); to the best of our
knowledge, there have been no efforts towards evalu-
ation methodologies that are semantically deeper than
this. This is possibly due to the issue of semidecid-
ability first-order logic and the inherent intractability
of theorem provers that presents a challenge for the
evaluation of test results. High level methodologies
typically do not specify the requirements in a verifi-
able form. In any case, the existing methodologies do
not sufficiently address the issue of ontology verifica-
tion, and our goal is to address this hole, in particular,
the challenges encountered in first-order logic devel-
opment.
3 CASE STUDY: AN ONTOLOGY
FOR FLOW MODELLING
The motivating scenarios which initiated this work
and which will be used to illustrate the different
phases of the ontology lifecycle are based on an ef-
fort to provide a process ontology for flow modelling
formalisms such as UML activity diagrams, BPMN,
and IDEF3. For example, consider the UML activity
diagram in Figure 1; any process ontology that cap-
tures the intended semantics of such a diagram needs
to be able represent the constraints that are implicit in
the notions of split/merge and fork/join nodes. Intu-
itively, there are three possible ways in which the pro-
cess described by the activity diagram can occur; in
all three occurrences of the process, there is an initial
occurrence of the subactivity A and a final occurrence
of the subactivity E. One occurrence of the process
contains an occurrence of the subactivity F, while the
other two contain occurrences of the subactivities B,
C, and D. In order to developsuch an ontology, we be-
gan with the Process Specification Language (PSL),
but in order to capture the intended semantics of the
UML constructs, we also needed to develop an exten-
sion to the ontology that explicitly captured the asso-
ciated ordering and occurrence constraints.
In this section, we give a brief introduction of the
PSL Ontology and an overviewof the relations for the
extension to the PSL Ontology. Throughout the re-
mainder of the paper, we will follow the development
of this extension from the specification of the initial
requirements to the verification of the proposed ax-
A
B
F
D
C
E
Figure 1: Example of a UML activity diagram.
iomatization.
3.1 The PSL Ontology
The Process Specification Language (PSL) (Bock
and Gr¨uninger, 2004; Gr¨uninger, 2009b; Gr¨uninger,
2003) has been designed to facilitate correct and com-
plete exchange of process information.
1
The primary
purpose of PSL is to enable the semantic interop-
erability of manufacturing process descriptions be-
tween manufacturing engineering and business soft-
ware applications such as process planning, schedul-
ing, workflow, and project management. Additional
applications of PSL include business process design
and analysis, the implementation of business pro-
cesses as web services, and enterprise modelling.
The PSL Ontology is a modular set of theories
in the language of first-order logic. All core theo-
ries within the ontology are consistent extensions of
a theory referred to as PSL-Core, which introduces
the basic ontological commitment to a domain of ac-
tivities, activity occurrences, timepoints, and objects
that participate in activities. Additional core theories
capture the basic intuitions for the composition of ac-
tivities, and the relationship between the occurrence
1
PSL has been published as an International Standard
(ISO 18629) within the International Organisation of Stan-
dardisation. The full set of axioms (which we call T
psl
)
in the Common Logic Interchange Format is available at
http://www.mel.nist.gov/psl/ontology.html.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
38

of a complex activity and occurrences of its subactiv-
ities.
In order to formally specify a broad variety of
properties and constraints on complex activities, we
need to explicitly describe and quantify over com-
plex activities and their occurrences. Within the
PSL Ontology, complex activities and occurrences
of activities are elements of the domain and the
occurrence of relation is used to capture the relation-
ship between different occurrences of the same activ-
ity.
A second requirement for formalising queries is
to specify composition of activities and occurrences.
The PSL Ontology uses the subactivity relation to
capture the basic intuitions for the composition of ac-
tivities. Complex activities are composed of sets of
atomic activities, which in turn are either primitive
(i.e., they have no proper subactivities) or they are
concurrent combinations of primitive activities.
Corresponding to the composition relation over
activities, subactivity occurrence is the composition
relation over activity occurrences. Given an occur-
rence of a complex activity, subactivity occurrences
are occurrences of subactivities of the complex activ-
ity.
Finally, we need some way to specify order-
ing constraints over the subactivity occurrences of
a complex activity. The PSL Ontology uses the
min precedes(s
1
, s
2
, a) relation to denote that subac-
tivity occurrence s
1
precedes the subactivity occur-
rence s
2
in occurrences of the complex activity a.
Note that there could be other subactivity occurrences
between s
1
and s
2
. We use next subocc(s
1
, s
2
, a) to
denote that s
2
is the next subactivity occurrence after
s
1
in occurrences of the complex activity a.
The basic structure that characterises occurrences
of complex activities within models of the ontology
is the activity tree, which is a subtree of the legal oc-
currence tree that consists of all possible sequences
of atomic subactivity occurrences of an activity; the
relation root(s, a) denotes that the subactivity occur-
rence s is the root of an activity tree for a. Elements
of the tree are ordered by the min precedes relation;
each branch of an activity tree is a linearly ordered set
of occurrences of subactivities of the complex activ-
ity. The same tree(s
1
, s
2
, a) is used to denote that s
1
and s
2
are both elements of the same activity tree for
a. Finally, there is a one-to-one correspondence be-
tween occurrences of complex activities and branches
of the associated activity trees.
In a sense, an activity tree is a microcosm of the
occurrence tree, in which we consider all of the ways
in which the world unfolds in the context of an oc-
currence of the complex activity. Different subactiv-
ities may occur on different branches of the activity
tree — different occurrences of an activity may have
different subactivity occurrences or different order-
ings on the same subactivity occurrences. The rela-
tion mono(s
1
, s
2
, a) indicates that s
1
and s
2
are occur-
rences of the same subactivity on different branches
of the activity tree for a.
3.2 Subactivity Occurrence Orderings
The approach taken in the development of the new
extension to the PSL Ontology is to represent flow
models such as UML activity diagrams as a partial
ordering over a set of subactivity occurrences. This
partial ordering is embedded into an activity tree such
that the branches of the activity tree correspond to a
set of linear extensions for suborderings of the partial
ordering. For example, the subactivity occurrence or-
dering corresponding to the UML activity diagram in
Figure 1 can be found in Figure 2, while the activity
tree into which this partial ordering is embedded can
be found in Figure 3.
o
A
1
o
B
2
o
C
3
o
D
4
o
E
5
o
F
6
Figure 2: Example of a subactivity occurrence ordering.
Three relations are introduced to specify the rela-
tionship between the partial ordering (referred to as
the subactivity occurrence ordering) and the activ-
ity tree. The relation soo(s, a) denotes that the ac-
tivity occurrence s is an element of the subactivity
occurrence ordering for the activity a. The relation
soo precedes(s
1
, s
2
, a) captures the ordering over the
elements. For example
2
, the partial ordering in Figure
2 can be defined by:
soo(o
A
1
, a) ∧ soo(o
B
2
, a), soo(o
C
3
, a) ∧ soo(o
D
4
, a)
∧ soo(o
E
5
, a) ∧ soo(o
6
, F) ∧ soo precedes(o
A
1
, o
B
2
, a)
∧ soo precedes(o
B
2
, o
C
3
, a) ∧ soo precedes(o
C
3
, o
E
5
, a)
2
Each activity occurrence is an occurrence of a unique
activity but activities can have multiple occurrences, so we
label activity occurrences using the following convention:
for activity occurrence o
j
i
, i is a unique label for the occur-
rence and j denotes the activity of which it is an occurrence.
For example, o
C
3
and o
C
7
are two occurrences of the activity
C.
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE
39
∧ soo precedes(o
B
2
, o
D
4
, a) ∧ soo precedes(o
D
4
, o
E
5
, a)
∧ soo precedes(o
A
1
, o
F
6
, a) ∧ soo precedes(o
F
6
, o
E
5
, a)
(1)
and the activity tree in Figure 3 can be specified by
min precedes(o
A
1
, o
B
2
, a) (2)
∧ min precedes(o
B
2
, o
C
3
, a) ∧ min precedes(o
C
3
, o
D
4
, a)
∧ min precedes(o
D
4
, o
E
5
, a) ∧ min precedes(o
B
2
, o
D
6
, a)
∧ min precedes(o
D
6
, o
C
7
, a) ∧ min precedes(o
C
7
, o
E
8
, a)
∧ min precedes(o
A
1
, o
F
9
, a) ∧ min precedes(o
F
9
, o
E
10
, a)
Two branches of the activity tree correspond
to linear extensions of the subordering of the par-
tial ordering in Figure 2 consisting of the elements
{o
A
1
, o
B
2
, o
C
3
, o
D
4
, o
E
5
} while the remaining branch corre-
sponds to the subordering consisting of the elements
{o
A
1
, o
F
6
, o
E
5
}.
Finally, the preserves(s
1
, s
2
, a) relation
holds whenever the mono relation preserves the
min precedes relation; that is, if s
1
min precedes
s
2
, then there is no element of the activity tree that
is mono to s
2
that min precedes an element of the
activity tree that is mono to s
1
.
o
A
1
o
B
2
o
C
3
o
D
4
o
E
5
o
D
6
o
C
7
o
E
8
o
F
9
o
E
10
Figure 3: An activity tree corresponding to the subactivity
occurrence ordering in Figure 2.
The complete set of axioms for the subactivity oc-
currence ordering extension to the PSL Ontology can
be found in Appendix A.
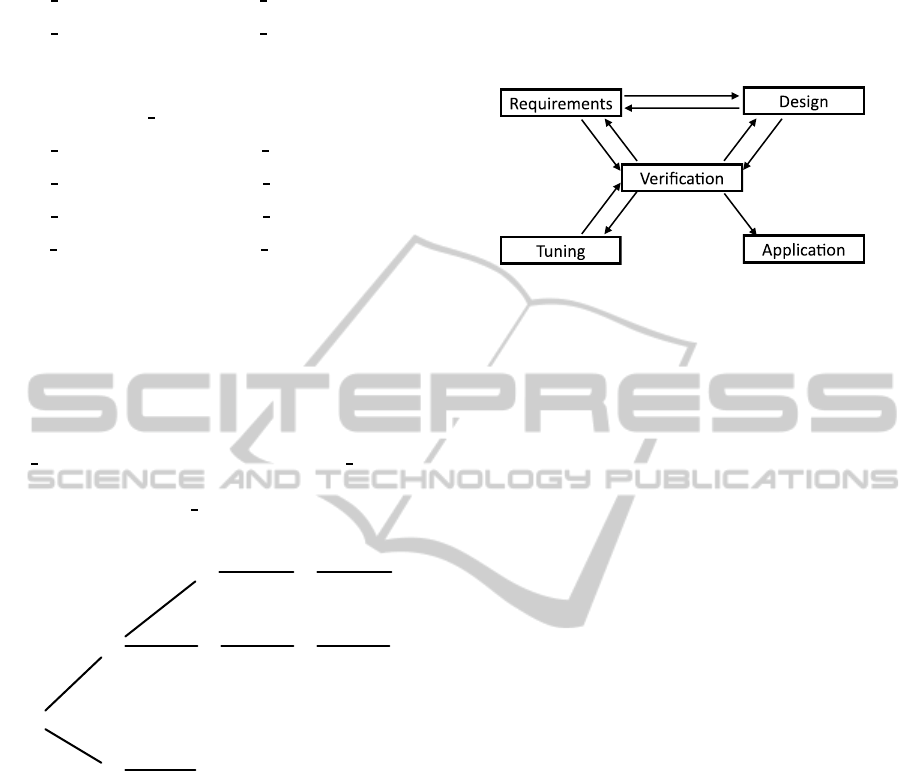
4 THE ONTOLOGY LIFECYCLE
The lifecycle presented in Figure 4 is intended to
serve as a structured framework that provides guid-
ance during the ontology development process. This
lifecycle addresses the limitations of existing verifi-
cation techniques while providing a structure within
which existing techniques for ontology design and re-
quirements identification may be applied. The feed-
back and interactions between the various phases il-
lustrates the tight integration between the design and
the verification of the ontology. Throughout this sec-
tion, we illustrate the efficacy of this lifecycle frame-
work using examples from the design and mainte-
nance of the PSL Ontology.
Figure 4: The Ontology Lifecycle.
We define five phases in the ontology lifecycle:
• The Requirements Phase produces a specification
of the intended models of the ontology arising
from a set of use cases (also referred to as motivat-
ing scenarios in (Uschold and Gr¨uninger, 1996))
• The Design Phase produces an ontology to axiom-
atize the class of models that capture the require-
ments. The feedback loop that is shown in Fig-
ure 4 between the Design Phase and the Require-
ments Phase occurs as the ontology develops. In
the Requirements Phase the intended models must
initially be specified informally, until the design
of the ontology has matured such that its require-
ments may be specified using its vocabulary.
• The Verification Phase guarantees that the in-
tended models of the ontology which are speci-
fied in the Requirements Phase are equivalent to
the models of the axioms which are produced in
the Design Phase.
• The Tuning Phase addresses the pragmatic is-
sue of dealing with cases in which the theorem
provers used in the Verification Phase fail to re-
turn a definitive answer.
• The Application Phase covers the different ways
in which the ontology is used, such as decision
support systems, semantic integration, and search.
Each phase in the ontology lifecycle is associated
with a set of reasoning problems that are defined with
respect to the axioms of the ontology T
onto
, a domain
theory Σ
domain
that uses the ontology, and a query
Φ that formalizes the competency questions and On-
tological Stance scenarios produced in the Require-
ments Phase. Since these reasoning problems are en-
tailment problems of the form:
T
onto
∪ Σ
domain
|= Φ
we can utilize theorem provers to verify that the ax-
iomatization of the ontology satisfies its requirements.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
40

The relationships between the stages of the ontology
lifecycle and the different aspects of the reasoning
problems are shown in Figure 5.
The Design Phase provides the axioms T
onto
∪
Σ
domain
that form the antecedent of the reasoning
problem. In the Verification Phase, we use theorem
provers to determine whether or not the sentences that
capture the requirements are indeed entailed by the
axioms of the ontology.
Design
z }| {
T
onto
∪ Σ
domain
|=
Requirements
z}|{
Φ
| {z }
Verification
Figure 5: Reasoning problems and stages of the ontology
lifecycle.
4.1 Requirements
Requirements for an ontology are specified with re-
spect to the intended semantics of the terminology,
and the challenge of the initial phase of the ontology
lifecycle is to cast these requirements in a testable
form. From a mathematical perspective the require-
ments may be characterized by their intended models
(Section 4.1.1); to allow for semiautomatic verifica-
tion we specify these semantic requirements as en-
tailment problems, with the use of competency ques-
tions (Section 4.1.2) or the Ontological Stance (Sec-
tion 4.1.3). From a reasoning problem perspective the
output of the Requirements Phase is a set of conse-
quents for the entailment problems described above.
4.1.1 Intended Models
In current ontology research, the languages for for-
mal ontologies (such as RDFS, OWL, and Common
Logic) are closely related to mathematical logic, in
which the semantics are based on the notion of an in-
terpretation. If a sentence is true in the interpretation,
we say that the sentence is satisfied by the interpreta-
tion. If every axiom in the ontology is satisfied by the
interpretation, then the interpretation is called a model
of the ontology. With a formal ontology, the content
of the ontology is specified as a theory, so that a sen-
tence is consistent with that theory if there exists a
model of the theory that satisfies the sentence; a sen-
tence can be deduced if it is satisfied by all models of
the theory. Therefore, the semantics of the ontology’s
terminology can be characterized by this implicit set
of models, which we refer to as the set of intended
models.
Intended models are specified with respect to
some well-understood class of mathematical struc-
tures (such as partial orderings, graph theory, and ge-
ometry). The extensions of the relations in the model
are then specified with respect to properties of these
mathematical structures.
For example, the intended models for the subac-
tivity occurrence ordering extension to the PSL On-
tology are intuitively specified by two properties:
• the partial ordering over the subactivity occur-
rences;
• the mapping that embeds the partial ordering into
the activity tree.
Formally, the intended models for the subactivity oc-
currence ordering extension are defined by
Definition 1. Let M
soo
be the following class of
structures such that for any M ∈ M
soo
,
1. M is an extension of a model of T
psl
(i.e. the PSL
Ontology);
2. for each activity tree τ
i
, there exists a unique par-
tial ordering ρ
i
= (P
i
, ≺) and a mapping
θ : τ
i
→ ρ
i
such that
(a) hs
1
, s
2
, ai ∈ min precedes ⇒ θ(s
2
) 6≺ θ(s
1
)
(b) hθ(s), s, ai ∈ mono;
(c) comparable elements in ρ are the image of com-
parable elements in τ.
3. hs, ai ∈ soo iff s ∈ P
i
;
4. hs
1
, s
2
, ai ∈ soo precedes iff s
1
≺ s
2
.
Although one can take this approach to explicitly
specify the intended models as a class of mathemat-
ical structures, in practice the specification of the in-
tended models is based on use cases for the applica-
tion of the ontology. The two primary application ar-
eas for the PSL Ontology have been in semantic in-
tegration and decision support systems. In this ap-
proach, the intended models are defined implicitly
with respect either to the set of sentences that are
satisfied by all of the intended models or to sets of
sentences that should be satisfied by some model. If
we recall that sentences satisfied by all models are
entailed by the axiomatization, then this leads us to
the idea of implicitly defining the intended models of
the ontology with respect to reasoning problems. The
reasoning problems that are associated with the Re-
quirements Phase are competency questions (which
arise primarily from decision support use cases) and
Ontological Stance scenarios (which are motivated by
semantic integration use cases).
4.1.2 Competency Questions
Following (Gr¨uninger and Fox, 1995; Gruninger and
Fox, 1994; Uschold and Gr¨uninger, 1996), compe-
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE
41

tency questions are queries that impose demands on
the expressiveness of the underlying ontology. Intu-
itively, the ontology must be able to represent these
questions and characterize the answers using the ter-
minology. The relationship between competency
questions and the requirements is that the associated
query must be provable from the axioms of the ontol-
ogy alone. Since a sentence is provable if and only if
it is satisfied by all models, competency questions im-
plicitly specify the intended models of the ontology.
In the area of decision support, the verification of
an ontology allows us to make the claim that any in-
ferences drawn by a reasoning engine using the ontol-
ogy are actually entailed by the ontology’s intended
models. If an ontology’s axiomatization has unin-
tended models, then it is possible to find sentences
that are entailed by the intended models, but which
are not provable from the axioms of the ontology.
Examples of competency questions for the subac-
tivity occurrence ordering extension include the fol-
lowing:
Which subactivities can possibly occur next after
an occurrence of the activity a
1
?
(∀o, s
1
) occurrence(s
1
, a
1
) ∧ occurrence(o, a) (3)
∧ subactivity occurrence(s
1
, o)
⊃ (∃a
2
, s
2
) occurrence(s
2
, a
2
) ∧ next subocc(s
1
, s
2
, a))
Does there exist a point in an activity tree for a
after which the same subactivities occur?
(∃a, a
1
, s
1
) subactivity(a
1
, a) ∧ occurrence of(s
1
, a
1
)
∧ ((∀o
1
, o
2
) occurrence of (o
1
, a) ∧ occurrence of(o
2
, a)
∧ subactivity occurrence(s
1
, o
1
)
∧ subactivity occurrence(s
1
, o
2
)
∧ min precedes(s
1
, s
2
, a)
⊃ (∃s
3
) subactivity occurrence(s
3
, o
2
)
∧ min precedes(s
1
, s
3
, a) ∧ mono(s
2
, s
3
, a) (4)
Recall that sentences such as these constitute the
consequent Φ of a reasoning problem (see Figure 5),
and that they are supposed to be entailed by the ax-
ioms of the ontology T
onto
together with a domain the-
ory T
domain
(which in this case is a process description
that formalizes a specific UML activity diagram). It
is in this sense that competency questions are require-
ments for the ontology – there must be sufficient ax-
ioms in T
onto
∪ T
domain
to entail the sentences that for-
malize the competency questions.
4.1.3 Ontological Stance
We can say that two software systems are semanti-
cally integrated if their sets of intended models are
equivalent. However, systems cannot exchange the
models themselves – they can only exchange sen-
tences in the formal language that they use to repre-
sent their knowledge. We must be able to guarantee
that the inferences made with sentences exchanged in
this way are equivalent to the inferences made with
respect to the system’s intended models – given some
input the application uses these intended models to
infer the correct output. This leads to the notion of
the Ontological Stance (Gr¨uninger, 2009a) in which a
software application is described as if it were an in-
ference system with an axiomatized ontology which
is used to predict the set of sentences that the infer-
ence system decides to be satisfiable. What is of rele-
vance for the ontologylifecycle is that the Ontological
Stance does not directly postulate a specific set of ax-
ioms, but rather a set of intended models: Given an
application A, there exists a class of models M
A
such
that any sentence Φ is decided by A to be satisfiable
if and only if there exists a model M ∈ M such that
M entails Φ.
In the context of the subactivity occurrence order-
ing extension to the PSL Ontology, software appli-
cations that simulate flow modelling diagrams such
as UML or IDEF3 form the basis of the Ontologi-
cal Stance scenarios. Reasoning problems associated
with such software applications typically involve ex-
ecutability – a particular execution of the process a
involving some subactivity a
1
is a possible output of
the software application if and only if the following
sentence is entailed:
(∀o) occurrence(o, a) ⊃ (∃s) occurrence(s, a
1
)
∧ subactivity occurrence(s, o) (5)
As we saw earlier with competency questions, this
sentence constitutes the consequent of the reasoning
problem that will be the focus of the Verification
Phase (see Figure 5). The antecedent for the rea-
soning problem that corresponds to the Ontological
Stance is slightly different – T
onto
is the axiomatiza-
tion of the ontology for the software application while
T
domain
is the axiomatization of the input to the soft-
ware application.
4.2 Design
As we saw in Figure 5, the Design Phase produces
a set of axioms that is supposed to entail the com-
petency questions and Ontological Stance scenarios.
We do not prescribe a specific methodology for the
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
42

design of the axioms; rather the reasoning problems
associated with the Design Phase focus on the notion
of the design rationale for axioms. The task in this
case to characterize why specific axioms are required,
tracing each axiom back to the original set of require-
ments for the ontology.
4.3 Verification
As we saw earlier, existing approaches to ontology
verification focus on taxonomic relationships and ob-
vious logical criteria for ontology evaluation such as
consistency. Strictly speaking, we only need to show
that a model exists in order to demonstrate that a
first-order theory is consistent. Constructing a sin-
gle model, however, runs the risk of having demon-
strated satisfiability for a restricted case; for example,
one could construct a model of a process ontology in
which no processes occur, without realizing that the
axiomatization might mistakenly be inconsistent with
any theory in which processes do occur. We therefore
need a complete characterization of all models of the
ontology up to isomorphism.
In general, verification is concerned with the rela-
tionship between the intended models of an ontology
and the models of the axiomatization of the ontology.
From a mathematical perspective this is formalized
by the notion of representation theorems. From a rea-
soning problem perspective this amounts to evaluat-
ing the entailment problems, and we are able to per-
form this verification semiautomatically with the use
of a theorem prover.
4.3.1 Representation Theorems
Representation theorems are proven in two parts – we
first prove every structure in the class is a model of
the ontology and then prove that every model of the
ontology is elementary equivalent to some structure
in the class.
For the new extension T
soo
to the PSL Ontology,
the representation theorem is stated as follows:
Theorem 1. Any structure M ∈ M
soo
is isomorphic
to a model of T
soo
∪ T
psl
.
Any model of T
soo
∪ T
psl
is isomorphic to a struc-
ture in M
soo
.
The characterization up to isomorphism of the
models of an ontology through a representation theo-
rem has several distinct advantages. First, unintended
models are more easily identified, since the represen-
tation theorems characterize all models of the ontol-
ogy. We also gain insight into any implicit assump-
tions within the axiomatization which may actually
eliminate models that were intended. Second, any de-
cidability and complexityresults that have been estab-
lished for the classes of mathematical structures in the
representation theorems can be extended to the ontol-
ogy itself. Finally, the characterization of models sup-
ports the specification of semantic mappings to other
ontologies, since such mappings between ontologies
preserve substructures of their models.
Representation theorems are distinct from the no-
tion of the completeness of an ontology. A logical
theory T is complete if and only if for any sentence
Φ, either T |= Φ or T 6|= Φ. The ontologies that we
develop are almost never complete in this sense. Nev-
ertheless, we can consider representation theorems to
be demonstration that the ontology T
onto
is complete
with respect to its requirements (i.e. set of intended
models M
onto
). This allows us to say that T
onto
|= Φ
if and only if M
onto
|= Φ (that is, the ontology entails
a sentence if and only if the class of intended models
entails the sentence).
The typical way to prove the Representation Theo-
rem for an ontology is to explicitly construct the mod-
els of the ontology in the metatheory and then show
that these models are equivalent to the specification
of the intended models of the ontology using classes
of mathematical structures. As we saw with the spec-
ification of the intended models, an alternative to the
mathematical specification of the representation the-
orem is to employ a theorem prover to verify that the
models of the ontology are equivalent to the intended
models. Rather than proving the Representation The-
orem directly, we can utilize the specification of the
requirements for the ontology as competency ques-
tions and Ontological Stance scenarios. We can do
this by proving that the extensions of the relations in
the models of the ontology have properties that are
equivalent to those satisfied by the extensions of the
relations in the intended models. For example, the
subactivity occurrence ordering ρ introduced in the
definition of the intended models M
soo
is a partial or-
dering, and this corresponds to the competency ques-
tions which asserts that the soo precedes relation is
also a partial ordering, and hence is a transitive rela-
tion:
(∀s
1
, s
2
, s
3
, a) soo precedes(s
1
, s
2
, a) (6)
∧ soo precedes(s
2
, s
3
, a) ⊃ soo precedes(s
1
, s
3
, a)
This illustrates the technique of identifying com-
petency questions directly from the mathematical def-
inition of the intended models.
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE
43

4.3.2 Outcomes of Verification
As we have just seen, the reasoning problems as-
sociated with Verification support the proofs of the
Representation Theorem. In addition to the compe-
tency questions, this also involves proving proposi-
tions which demonstrate that the extensions of the re-
lations in the models of the ontology have the same
properties as the extensions of relations in the in-
tended models.
For a test of any given requirement, there are three
possible outcomes of the Verification Phase:
Case 1: Unintended Proof Found. In this case, a
proof was found of a sentence that contradicts the
intended semantics of the ontology. This is of-
ten encountered when the theorem prover finds
a proof without using all, or any clauses from
the proposition or query. Given this possibility,
a thorough inspection of all proofs found must be
performed; if this case is detected, it is indicative
of at least one of two possible errors with the on-
tology:
1. An examination of the proof may lead to the
identification of some axiom in the ontology
which is not entailed by the intended models;
in this case we must return to the Design Phase.
One such result with the design of the sub-
activity occurrence ordering extension T
soo
to
the PSL ontology arose when testing its consis-
tency with the first addition of T
soo
. A proof
was found, and normally this would indicate
an error in the set of definitions that was be-
ing tested. However, upon examination we re-
alized that the definition of the same tree rela-
tion made it inconsistent for any model of the
ontology to have an occurrence in the same ac-
tivity tree as the root of the tree:
T
soo
∪ T
psl
|= (∀s
1
, a) root(s
1
, a)
⊃ ¬(∃s
2
) same tree(s
1
, s
2
, a) (7)
This sentence should not be entailed by the in-
tended models of the PSL Ontology itself, yet
it was only identified when using the axioms of
T
soo
; it was a hidden consequence of the PSL
Ontology. In particular, it was the axiom below
from T
soo
that played the critical role in deriv-
ing the unintended sentence:
(∀s
1
, a)root(s
1
, a) ⊃ (∃s
2
) soo(s
2
, a)
∧ mono(s
1
, s
2
, a) ∧ same tree(s
1
, s
2
, a) (8)
As a result of this discovery, the axiom for
same tree was modified.
It is interesting to see the relationship between
this case and the failure of a potential represen-
tation theorem for the ontology. Part of the rep-
resentation theorem shows that a sentence that
is entailed by axioms is also entailed by the set
of intended models. Hidden consequences such
as we have just considered are counterexamples
to this part of the representation, since it is a
sentence that is provablefrom the axioms, yet it
is not entailed by the intended models. One can
either weaken the axioms (so that the sentence
is no longer provable), or one can strengthen
the requirements by restricting the class of in-
tended models (so that the sentence is entailed
by all intended models).
2. An examination of the proof may lead to the
detection of some error in the definition of the
requirements; in this case we must return to the
Requirements Phase. It is important to devote
considerable attention to the detection of this
possibility so that the ontology is not revised to
satisfy incorrect requirements.
We did not encounter an example of this in
our experiences, however it would be possible
for an error in the requirements specification
to lead to an unintended proof. As discussed
above, this type of error could be addressed by
strengthening the requirements.
Case 2: No Proof Found. As a result of the semi-
decidability of first-order logic and the inherent
intractability of automated theorem proving, if no
proof is found when testing for a particular re-
quirement then a heuristic decision regarding the
state of the lifecycle must be made. It could be the
case that no proof is found because the sentence
really is not provable; there may be a mistake in
the definition of the requirement that we are test-
ing, or there may be an error in the axiomatization
of the ontology, (i.e. we cannot prove that the re-
quirement is met because it is not met). However,
it could be the case that due to the intractability of
automated theorem provers, a proof exists but the
theorem prover is unable to find it (at least within
some time limit). To avoid unnecessary work,
some effort must be made to ensure that we are
as informed as possible when making this deci-
sion; in particular, previously encountered errors
and the nature of the requirement that we are at-
tempting to prove is satisfied must be taken into
account. The heuristic decision is a choice be-
tween the following options:
1. If we believe there may be some error in the
requirements or the design of the ontology, then
we must revisit the Requirements Phase or the
Design Phase, respectively. It is recommended
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
44

that the Requirements Phase is revisited first, as
generally a much smaller investment is required
to investigate the correctness of a requirement,
rather than that of the ontology.
In the course of proving the representation the-
orem for T
soo
, the theorem prover failed to
entail a property regarding the mono relation,
namely, that the mono relation should only hold
between different occurrences of the same sub-
activity. This requirement was initially ex-
pressed as the following proposition:
(∀s
1
, s
2
, o, a) mono(s
1
, s
2
, a) ∧ occurrence of(o, a)
∧ subactivity occurrence(s
1
, o)
⊃ ¬subactivity occurrence(s
2
, o) (9)
It seemed clear that the axiomatizations of the
mono relation should have restricted all satisfy-
ing models to instances where s
1
and s
2
were
not in the same activity tree. Returning to
the Requirements Phase, an examination of the
abovesentence led to the realization that the ax-
iomatization of the proposition had been incor-
rect. We had neglected to specify the condition
that s
1
was not the same occurrence as s
2
, (in
which case the subactivity occurrence relation
clearly holds for s
2
if it holds for s
1
). Once this
issue was addressed, we continued to the Ver-
ification Phase (no revisions were required to
the ontology’s design) and the theorem prover
was able to show that the ontology entailed the
corrected property, shown below.
(∀s
1
, s
2
, o, a) mono(s
1
, s
2
, a) ∧ occurrence of(o, a)
∧ subactivity occurrence(s
1
, o) ∧ (s
1
6= s
2
)
⊃ ¬subactivity occurrence(s
2
, o) (10)
The previous example was a case where the er-
ror that was corrected resulted from a misrep-
resentation of the intended semantics of the re-
quirements. Another interesting situation was
encountered where the requirements’ semantics
were redefined following a series of inconclu-
sive test results. Originally, T
soo
was to be a
conservative extension of PSL
3
. In part, this
meant that the axiomatization of T
soo
had to ac-
count for all of the kinds of activity trees that
were represented in PSL. One particular class
of activity trees was represented by the zigzag
relation, defined below.
3
A detailed discussion of conservative extensions and
the role that they play in ontology development can be
found in (Grau et al., 2009).
(∀s
1
, s
3
, a) zigzag(s
1
, s
3
, a) (11)
≡ (∃s
2
)preserve(s
1
, s
2
, a)
∧ preserve(s
2
, s
3
, a) ∧ ¬preserve(s
1
, s
3
, a)
With the inclusion of the zigzag class in T
soo
we
were unable to entail the transitivity of the pre-
serve relation. Review of the inconclusive test
results led to the belief that with the inclusion
of the zigzag class of activity trees:
T
soo
∪ T
psl
6|= (∀s
1
, s
2
, s
3
, a) preserve(s
1
, s
2
, a)
∧ preserve(s
2
, s
3
, a) ⊃ preserve(s
1
, s
3
, a)
(12)
Careful consideration of the situation led to the
decision that the ability of T
soo
to entail the tran-
sitivity of the preserve relation was more im-
portant than developing it as a non-conservative
extension of PSL. This decision resulted in
a change in the axiomatization of T
soo
, how-
ever this change represented a change in the
requirements. We were no longer consider-
ing the zigzag class, because we had revised
the requirements such that T
soo
did not have to
be a conservative extension of PSL. After this
change was implemented, we were able to suc-
cessfully prove that the axioms of the ontology
entailed the transitivity of the preserve relation.
2. If we are strongly confident about the correct-
ness of both the requirements and the design of
the ontology, then we consider the possibility
that it is the intractable nature of the theorem
prover that is preventing a proof from being
found. In this case, we proceed to the Tuning
Phase and attempt to adapt the ontology so that
the theorem prover performance is improved to
a level where the requirements can be verified.
In another case, we were unsuccessful in
proving a particular property about the
min precedes and the preserve relations.
Based on the intended semantics of the two
relations, it would appear straightforward that
in any model where min precedes holds for
two occurrences, preserve must hold as well.
We attempted to verify this by proving that we
could entail the following proposition from the
ontology with the theorem prover, however the
results were inconclusive:
(∀s
1
, s
2
, a)min precedes(s
1
, s
2
, a)
⊃ preserve(s
1
, s
2
, a) (13)
Being fairly certain about the correctness of the
ontology and specification of the property, we
moved to the Tuning Phase. In consideration of
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE
45

the definition of the preserve relation and the
proposition we were attempting to verify, the
reflexivity of the preserve relation was an intu-
itively important property. Two lemmas regard-
ing the reflexivity of the mono relation that had
already been shown to satisfy the models of the
ontology were:
(∀s
1
, s
2
, a)min precedes(s
1
, s
2
, a)
⊃ mono(s
2
, s
2
, a) (14)
and
(∀s, o, a)subactivity occurrence(s, o) ∧ legal(s)
∧ occurrence of(o, a) ⊃ mono(s, s, a) (15)
The addition of these lemmas to the original
reasoning problem aided the theorem prover
sufficiently so that the property was proved and
we could continue testing the other require-
ments.
This example illustrates a phenomenon that
distinguishes theorem proving with ontologies
from more traditional theorem proving – we are
not certain that a particular sentence is actually
provable. Effectively, every theorem proving
task with an ontology is an open problem.
Case 3: All Requirements Met. If we obtain a
proof that a requirement is satisfied, and it is
consistent with the intended semantics of the
ontology, then we may proceed with testing the
remaining requirements. Once we obtain such
proofs for each requirement, the ontology we
have developed satisfies our requirements and we
can proceed to the Application Phase.
Note that the results of the Verification Phase may
lead to revisions of either the design or the require-
ments of the ontology. The Design Phase is revis-
ited in the case that an error is detected or suspected
in the Verification Phase. If an error in the design is
identified, it is noted that the developer must be cau-
tious and consider the entire design when making the
correction so that further errors are not created. Ad-
ditionally, when a correction is made to the design,
all previous test results should be reviewed, and any
tests (proofs) that were related to the error should be
rerun; an error in the design has the potential to posi-
tively or negatively impact the results of any tests run
prior to its identification and correction. The Require-
ments Phase is revisited in the case that an error in the
requirements is found or suspected during the Verifi-
cation Phase. It may also be revisited if revisions to
the requirements are necessary because of corrections
to the ontology that were implemented in the Design
Phase.
4.4 Tuning
The Tuning Phase focuses on the mitigation of theo-
rem prover intractability. Similar to the Design Phase,
the Tuning Phase develops a set of axioms, however
the input and the function of each phase makes the
two distinct. In contrast to the Design Phase, the in-
put of the Tuning Phase is a version of the ontology
that we believe to be correct, but have not been able to
conclusively test. Automated theorem provers some-
times have difficulty finding a proof, though one ex-
ists; the aim of this phase is to apply techniques to
streamline the ontology in an effort to mitigate theo-
rem prover intractability. This can be accomplished
with the development of subsets and the use of lem-
mas, discussed in further detail below.
To develop a subset requires that we remove some
of the axioms of the ontology that are not relevant (in
the axiomatization of the ontology) to the particular
reasoning problem we are considering. The idea is
that by excluding these axioms from the reasoning
problem, we can increase the efficiency of the theo-
rem prover, as it will not be considering axioms that
would not be used for the proof. By reducing the
number of clauses that must be considered by the the-
orem prover, there is the potential to reduce the time
required to find a solution, if one exists. The selec-
tion of a subset could be, but is not necessarily based
on the modules of an ontology. Our work with the
PSL ontology often led to breaking up the axioms in a
module. We have currently not explored all aspects of
this technique in depth, however it appears that sub-
set selection introduces a new complication that must
be considered. When selecting a subset of the ontol-
ogy, we must ensure that all of the necessary axioms
have been included. If any related axiom is excluded,
this could allow for an inconclusive test result (we
might not prove a sentence because some of the ax-
ioms required to prove it have been excluded). At this
point, we do not provide any methodology to address
this challenge; a clear and complete understanding of
the ontology is required to be certain of what axioms
must be selected for a subset for a particular reasoning
problem.
For example, when working with the PSL ontol-
ogy, we could exclude axioms from PSL-Core that
had to do with timepoints when testing reasoning
problems that were related to the composition of ac-
tivities. This was possible because of our understand-
ing of the concepts of the ontology. The size of the
PSL ontology makes the use of subsets necessary for
most reasoning problems, however we have observed
that these subsets are often successfully reused for
other related reasoning problems. While testing the
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
46

ontology, we were able to use the same subset
4
to
successfully entail 14 of 16 propositions related to the
ordering of subactivity occurrences. .
We use the term lemma in its traditional, mathe-
matical sense. Their use to improve theorem prover
performance is a commonly accepted technique. In
the Tuning Phase, we can apply this technique to as-
sist in obtaining conclusive test results. Lemmas may
be used (in conjunction or independent of subsets)
to improve performance as a means of reducing the
number of steps required to obtain a proof. By adding
a lemma, we hope to provide the theorem prover with
a sentence that will be used in the proof; in this case
the number of steps required to obtain the proof is
reduced (since the theorem prover no longer needs
to prove the lemma before using it). We also spec-
ulate that the addition of such a lemma provides a
sort of guidance for the search, in the direction of
the desired proof. Lemmas should be developed in-
telligently, with some idea of how the addition of the
sentence to the ontology will assist in finding a proof.
Another point to consider is that of reusability. Some
effort should be made to design a lemma that is gen-
eral enough to be applied for other reasoning prob-
lems. In the event that we have already developed
a lemma for one reasoning problem, we should con-
sider its potential use in the Tuning Phase for a related
reasoning problem.
An example of the use of a lemma while testing
the PSL ontology is discussed in Case 2 in the previ-
ous section.
5 DISCUSSION
The description of the Verification Phase in Sec-
tion 4.3.2 highlighted the heuristic decisions in the
methodology that result from the semidecidability
of first-order logic, and the intractability of theorem
proving in this case. As discussed, if we do not obtain
a proof when testing a requirement, then we cannot be
certain if this is because a proof does not exist (if this
is the case, then we know that our current ontology
does not satisfy the requirement, unless it was incor-
rectly specified) or if a proof does exist but the theo-
rem prover reaches a specified time limit before it is
able to find it (this would present us with either Case
1 or Case 2, as described above). We suspect that it
is this issue of uncertain paths resulting from Case 2
that will stimulate some criticism of our verification
methodology and the lifecycle as it is proposed here.
We address this concern with the following remarks:
4
This subset can be found at http://stl.mie.utoronto.ca/
colore/process/psl-subset-519.clif.
• In two of the three possible cases that we have
identified, we can be certain of the direction we
must proceed in (the cases when a proof is found).
• In Case 2, when a proof is not found and there
is uncertainty about the cause, we can be certain
that the requirements for the ontology’s applica-
tion have not been met. Applications of the ontol-
ogy that utilize a theorem prover must be able to
answer a query (competency questions) or entail
a proposition (infer a property). In other words a
theorem prover must be able to find a proof of the
requirements in some reasonable amount of time.
Therefore, we can say that in all cases the verifi-
cation methodology is capable of testing if the re-
quirements are met; the uncertainty exists in how
to proceed in development when a requirement is
not met.
• The uncertainty of which path should be followed
when a requirement is not met may be mitigated.
If thorough documentation practices are followed
through development, we may seek out trends to
indicate the most likely source of the error. Addi-
tionally, sometimes a model building tool may be
used to test for the existence of counterexamples.
• Furthermore, we havedemonstrated the feasibility
and effectiveness of our methodology in practice
with examples of each possible case in the Verifi-
cation Phase.
6 FUTURE WORK
One direction of future work that arose from the de-
velopment of the subactivity occurrence ordering ex-
tension of PSL is in the area of development envi-
ronments. Specifically, an environment capable of
capturing the development history of an ontology -
including test results, changes made to axioms and
requirements, and different versions of the ontology
developed in the Tuning Phase. This would be valu-
able not only from a documentation perspective, but
as a potential aid to heuristic decisions. A summary
of test results could indicate trends (design errors, or
lemmas required) that would assist the decision pro-
cess in the case that no proof is found. Also, if a
particular test remains inconclusiveafter considerable
effort, an environment capable of tracking test details
could allow the developer to temporarily leave the test
unresolved and return to it after additional tests have
been performed. With the necessary test history in-
formation available, the developer could easily and
efficiently apply any corrections, subsets, or lemmas
discovered in subsequent tests to the “problem” test.
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE
47

An environment dedicated to this type of documen-
tation has the potential to be theorem prover indepen-
dent. This would be beneficial since different theorem
provers may be more useful for different applications
or with different ontologies, so committing to one the-
orem prover restricts the potential application of the
methodology presented here.
Additional areas for future work that we have
identified are briefly described below:
• Perform experiments to identify the possibility of
problem-general heuristics or techniques to re-
duce uncertainty in the heuristic decision follow-
ing a Case 2 of the Verification Phase.
• Include maintenance considerations in the lifecy-
cle phases. Different types of maintenance activi-
ties (bug fixes, changes in the ontology’s domain)
should be performed differently within the lifecy-
cle.
• Explore and expand on the presence of model gen-
eration as a tool for testing in the Verification
Phase.
• Investigate the role of non-functional require-
ments in the ontology lifecycle. In keeping with
the analogy typically drawn between software and
ontology development, we identify the specifica-
tion of intended models as the functional require-
ments of an ontology. This leaves the design and
evaluation of non-functional requirements to be
explored: how can these qualities be identified
and measured? and how can they be integrated
in the development lifecycle of ontologies?
7 CONCLUSIONS
Existing ontology development methodologies do not
provide an account of ontology evaluation that is ad-
equate for verifying ontologies with respect to their
model-theoretic properties. In this paper, we have
provided an approach to the ontology lifecycle that
focuses on support for semiautomatic verification of
ontologies, including a methodology that takes into
account the pragmatic issues of semi-decidability in
first-order logic. The effective use of such a method-
ology addresses the challenges posed by ontologies
that use more expressivelanguages, such as first-order
logic.
Our presentation of the ontology lifecycle rests on
the connection between the mathematical definition
of the intended models of an ontology and the rea-
soning problems that are equivalent to the verification
of these intended models with respect to the axiom-
atization of the ontology. It is this connection which
allows theorem provers to play a pivotal role in ontol-
ogy design, analysis, and evaluation.
Nothing in the methodology and semiautomatic
verification presented here is specific to the PSL on-
tology, or to first-order logic. The lifecycle accounts
for the difficulties of development with first-order
logic; however, since the semiautomatic verification
of requirements satisfaction could be beneficial in any
application of ontology development, we close with
an invitation for the techniques presented here to be
applied with other ontologies.
REFERENCES
Bock, C. and Gr¨uninger, M. (2004). PSL: A semantic do-
main for flow models. Software and Systems Model-
ing, 4:209–231.
Fern´andez, M., G´omez-P´erez, A., and Juristo, N. (1997).
Methontology from ontological art towards ontologi-
cal engineering. In Symposium on Ontological Engi-
neering of AAAI.
G´omez-P´erez, A., Corcho, O., and Fern´andez-Lopez,
M. (2004). Ontological Engineering : with ex-
amples from the areas of Knowledge Management,
e-Commerce and the Semantic Web. First Edition
(Advanced Information and Knowledge Processing).
Springer.
Grau, B., Parsia, B., and Sirin, E. (2009). Ontology inte-
gration using e-connections. In Modular Ontologies,
pages 293–320. Springer-Verlag, Berlin.
Gr¨uninger, M. (2003). Ontology of the process specification
language. In Handbook of Ontologies, pages 599–618.
Springer-Verlag, Berlin.
Gr¨uninger, M. (2009a). The ontological stance for a man-
ufacturing scenario. Journal of Cases in Information
Systems, 11:1–25.
Gr¨uninger, M. (2009b). Using the PSL ontology. In Hand-
book of Ontologies, pages 419–431. Springer-Verlag,
Berlin.
Gruninger, M. and Fox, M. S. (1994). The role of compe-
tency questions in enterprise engineering. In Proceed-
ings of the IFIP WG5.7 Workshop on Benchmarking –
Theory and Practice.
Gr¨uninger, M. and Fox, M. S. (1995). Methodology for the
design and evaluation of ontologies. In International
Joint Conference on Artificial Inteligence (IJCAI95),
Workshop on Basic Ontological Issues in Knowledge
Sharing.
Pinto, H. S., Tempich, C., and Staab, S. (2003). Ontology
engineering and evolution in a distributed world using
diligent. In Handbook on Ontologies, International
Handbooks on Information Systems, pages 153–176.
Springer.
Sure, Y., Staab, S., Studer, R., and Gmbh, O. (2003). On-
to-knowledge methodology (otkm). In Handbook on
Ontologies, International Handbooks on Information
Systems, pages 117–132. Springer.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
48

Uschold, M. and Gr¨uninger, M. (1996). Ontologies: Princi-
ples, methods and applications. Knowledge Engineer-
ing Review, 11:93–136.
Uschold, M. and King, M. (1995). Towards a methodol-
ogy for building ontologies. In In Workshop on Ba-
sic Ontological Issues in Knowledge Sharing, held in
conjunction with IJCAI-95.
APPENDIX
Axioms for Subactivity Occurrence
Orderings
Elements of the subactivity occurrence ordering are
elements of an activity tree.
(∀a, s) soo(s, a) ⊃ (16)
root(s, a) ∨ (∃s
1
) min precedes(s
1
, s, a)
The root of an activity tree is mapped to an el-
ement of the subactivity occurrence ordering by an
order homomorphism.
(∀s
1
, a) root(s
1
, a) ⊃ (17)
(∃s
2
)soo(s
2
, a)∧mono(s
1
, s
2
, a)∧same tree(s
1
, s
2
, a)
Every element of the activity tree is mapped to an
element of the subactivity occurrence ordering by an
order homomorphism.
(∀s
1
, s
2
, a) min precedes(s
1
, s
2
, a) ⊃ (18)
(∃s
3
)soo(s
3
, a)∧mono(s
2
, s
3
, a)∧same tree(s
3
, s
2
, a)
There is no order homomorphismbetween distinct
elements of the subactivity occurrence ordering.
(∀s
1
, s
2
, a) mono(s
1
, s
2
, a) ∧ soo(s
1
, a) ∧ soo(s
2
, a)
(19)
∧same tree(s
1
, s
2
, a) ⊃ (s
1
= s
2
)
The relation soo precedes is transitive.
(∀a, s
1
, s
2
, s
3
) soo precedes(s
1
, s
2
, a)∧ (20)
soo precedes(s
2
, s
3
, a) ⊃ soo precedes(s
1
, s
3
, a)
The relation soo precedes orders elements in the
subactivity occurrence ordering.
(∀a, s
1
, s
2
) soo precedes(s
1
, s
2
, a) ≡ (21)
(soo(s
1
, a) ∧ soo(s
2
, a)
∧preserve(s
1
, s
2
, a) ∧ ¬preserve(s
2
, s
1
, a))
(∀s
1
, s
2
, a) preserve(s
1
, s
2
, a) ≡ (22)
(∃s
3
, s
4
) mono(s
1
, s
3
, a) ∧ mono(s
2
, s
4
, a)
∧min precedes(s
3
, s
4
, a)
∧same tree(s
1
, s
2
, a) ∧ same tree(s
1
, s
3
, a)
THEOREM PROVING IN THE ONTOLOGY LIFECYCLE
49
