GRAPHLET DATA MINING OF ENERGETICAL INTERACTION

PATTERNS IN PROTEIN 3D STRUCTURES

Carsten Henneges, Marc R¨ottig

Center for Bioinformatics T¨ubingen, Eberhard Karls Universit¨at T¨ubingen, Sand 1, T¨ubingen, Germany

Oliver Kohlbacher, Andreas Zell

Center for Bioinformatics T¨ubingen, Eberhard Karls Universit¨at T¨ubingen, Sand 1, T¨ubingen, Germany

Keywords:

Graphlets, Data Mining, Relative Neighbourhood Graph, Secondary Structure Elements, Decision Tree Model

Selection

Abstract:

Interactions between secondary structure elements (SSEs) in the core of proteins are evolutionary conserved

and deﬁne the overall fold of proteins. They can thus be used to classify protein families. Using a graph

representation of SSE interactions and data mining techniques we identify overrepresented graphlets that can

be used for protein classiﬁcation. We ﬁnd, in total, 627 signiﬁcant graphlets within the ICGEB Protein Bench-

mark database (SCOP40mini) and the Super-Secondary Structure database (SSSDB). Based on graphlets,

decision trees are able to predict the four SCOP levels and SSSDB (sub)motif classes with a mean Area Under

Curve (AUC) better than 0.89 (5-fold CV). Regularized decision trees reveal that for each classiﬁcation task

about 20 graphlets sufﬁce for reliable predictions. Graphlets composed of ﬁve secondary structure interactions

are most informative. Finally, we ﬁnd that graphlets can be predicted from secondary structure using decision

trees (5-fold CV) with a Matthews Correlation Coefﬁcient (MCC) reaching up to 0.7.

1 INTRODUCTION

Secondary structure elements (SSEs), β-sheets and

α-helices, are important building blocks of proteins

and interactions between these SSEs stabilize protein

tertiary structures. Many categorization schemes are

based on these SSEs like the SCOP (Murzin et al.,

1995) or CATH (Orengo et al., 1997) databases. For

example, the SCOP categorization scheme has four

levels, each one giving more detailed information

about the SSEs of a protein domain and the arrange-

ment of its SSEs.

An important question, especially in the context

of SSE-based categorization schemes like SCOP, is

whether there are interaction patterns between these

SSEs that occur preferably in native protein structures

or in protein structures of a given fold or superfamily.

As SSEs are complex three-dimensional structures,

whose relative states are hard to encode, analysing

the SSE interactions in full atomic detail can be-

come complex. However, encoding energetic inter-

action between SSEs as graphs makes this problem

amenable for graph-based analysis of protein struc-

tures. The SSEs of a structure are mapped to vertices

of a graph, and interactions between SSEs are repre-

sented by edges. Graph mining methods (Vacic et al.,

2010) can then be applied on these reduced represen-

tations of protein structures.

In the following sections, we mine these graph rep-

resentations for subgraphs, termed graphlets, that

preferably occur in native protein structures. The sig-

niﬁcance of a graphlet is statistically tested using a

random graph model, serving as a background model

(Milo et al., 2002). This background model allows us

to identify graphlets that occur more often in protein

graphs than in random graphs. The value of the ex-

tracted graphlets is then demonstrated by using them

in predictors for SCOP levels and SSSDB motifs.

2 MATERIALS AND METHODS

Databases

We perform our experiments using protein struc-

tures from the SCOP40mini dataset from the ICGEB

database and the database of super-secondary struc-

190

Henneges C., Röttig M., Kohlbacher O. and Zell A..

GRAPHLET DATA MINING OF ENERGETICAL INTERACTION PATTERNS IN PROTEIN 3D STRUCTURES.

DOI: 10.5220/0003077501900195

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages

190-195

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

tures SSSDB (Sonego et al., 2007; Chiang et al.,

2007).

Protein Preparation

We use C++ routines and the BALL library

(Kohlbacher and Lenhof, 2000) to analyse protein

structures. As a ﬁrst step, hydrogen atoms are added.

After a consistency check of each residue, we assign

partial charges and atom radii to atoms according to

the AMBER force ﬁeld. Finally, all hetero residues

are removed from the structure.

To be independent from protein annotation, all

SSEs are recomputed using the DSSP algorithm

(Kabsch and Sander, 1983), afterwards all residues

within loops are removed. α-helices are not further

modiﬁed, whereas all connected components of β-

strands linked by hydrogen bonds are merged into β-

sheets. In this way, each β-sheet is treated as a com-

plete 3D structure during the computation of interac-

tion energies.

Graphical Encoding of Energetic SSE

Interactions

To prepare the graph construction, we compute the

pairwise matrix of SSE interaction energies. Let A

and B be any secondary structures in a protein, and

let E[A, B, ...] be the AMBER energy of a set of SSEs,

then the pairwise interaction energy I[A, B] is given as

I[A, B] = E[A, B] − E[A] − E[B]. (1)

Graph construction serves for structural normal-

ization as well as extracting the interaction model.

It ﬁlters needless relations, while being independent

from the computed amount of I[A, B] energy and the

relative distance of the SSEs. Therefore, it makes pro-

teins having different numbers of SSEs comparable.

One convenient graph for this task is the Relative

Neighbourhood Graph (RNG) (Toussaint, 1980). The

RNG connects two labelled SSE nodes if the follow-

ing edge condition

I[A, B] ≤ max

{I[A,C], I[B,C]}, (2)

holds, where A, B,C are SSEs from the protein and

A 6= B 6= C. The RNG is a connected proximity graph

and, therefore, also connects SSEs that are too distant

for direct protein residue contacts. As its edge con-

dition resembles an ultra-metric (Milligan and Isaac,

1980), the RNG has shown great robustness in prac-

tice and is a powerful tool to extract meaningful per-

ceptual structures (Toussaint, 1980).

Graphlet Analysis

Graphlet analysis makes use of subgraph sampling

and, therefore, relies on a graph isomorphism test.

Each sampled subgraph is referred to as graphlet and

its frequency or probability within a network is esti-

mated by repeated sampling. In addition, statistical

graphlet analysis requires the knowledge of a back-

ground distribution to compute the probability of an

observation. As no analytical distribution function for

graphlets is known, their probabilities are in general

estimated from random graphs.

To obtain a random model resembling the input

graph distribution, each protein graph is randomized.

We use a random rewiring method where each edge

is split into two half-edges. Then, all half-edges are

randomized and rewired. This is repeated until a con-

nected graph is obtained or a maximum number of

iterations is reached. In the latter case, the last sam-

ple is saved. In summary, random rewiring conserves

important graph properties (e.g. the node degree). By

randomizing each graph once, we obtain a collection

of random graphs that closely resembles the test dis-

tribution.

Next, we estimate the graphlet distribution by ran-

dom sampling connected subgraphs. The goal of

the sampling is twofold: First, all existent graphlets

should be detected and, second, their distribution

should be estimated correctly. If all graphlets were

known in advance, drawing a ﬁxed number of samples

would yield the maximum likelihood estimate of the

graphlet distribution, which is a multinomial distribu-

tion (Wassermann, 2004; Georgii, 2004). To achieve

this estimate, we employ a two-pass approach for this

task.

In the ﬁrst pass, the data is exploratory sampled.

For counting the graphlet frequencies, we make use

of a Move-to-Front (MF) list that holds a counter for

each graphlet type. Thus, each sampled graphlet is

ﬁrst searched in the MF list for counting its occur-

rence and inserted in the case it is not found. There-

fore, the MF list length increases during this pass. We

draw 1000 samples per graph of the database to min-

imize the possibility of missing patterns.

In the second pass, we keep the MF list ﬁxed dur-

ing sampling to compute the maximum likelihood es-

timates. Again, we draw a total of 1000 samples, 5

repetitions with 200 samples, from each graph and,

thus, obtain 5 independent distribution estimates. If

sampling detects an unknown graphlet within the sec-

ond pass, a counter for unknownpatterns is increased.

Finally, we compute the distribution estimate by aver-

aging and normalizing all samplings for a graph.

We choose a sampling size of 1000 graphlets in

GRAPHLET DATA MINING OF ENERGETICAL INTERACTION PATTERNS IN PROTEIN 3D STRUCTURES

191

each phase because only a small fraction of the RNG

comprises more than 40 nodes, i.e., only a small frac-

tion of the database proteins are large. As the number

of graphlets increases exponentially with pattern size,

a trade-off between estimation accuracy and runtime

is required. We found that a sampling size of 1000 is

sufﬁcient to accurately estimate the graphlet distribu-

tion within a reasonable runtime.

To determine signiﬁcant graphlets, we employ

permutation testing, which is a non-parametric tech-

nique to efﬁciently test the equality of two distribu-

tions g, h (Wald and Wolfowitz, 1944). It requires no

assumptions on the true probability distributions. By

resampling new random distributions from the input

distribution and evaluating a test statistic T, it infers

the distribution of T under H

: g = h. This denotes

the case where g and h are equal and, therefore, al-

lows to compute the p-value for the hypothesis that

the input distributions are equal. In our experiments,

we use the

coin

package implemented in

(R Devel-

opment Core Team, 2009).

For each graphlet, we employ permutation testing

to compute the likelihood that its distribution on the

protein graphs equals its distribution on the random-

ized graphs. Hence, we determine those graphlets that

are signiﬁcantly over or under-represented in random

graphs. To account for the multiple-testing problem,

we afterwards adjust the p-values according to the

method of (Holm, 1979). Finally, all graphlets be-

low a signiﬁcance threshold of 0.05 and having a fre-

quency ratio at least 10-fold larger on protein graphs

than on the random graphs are retained for further

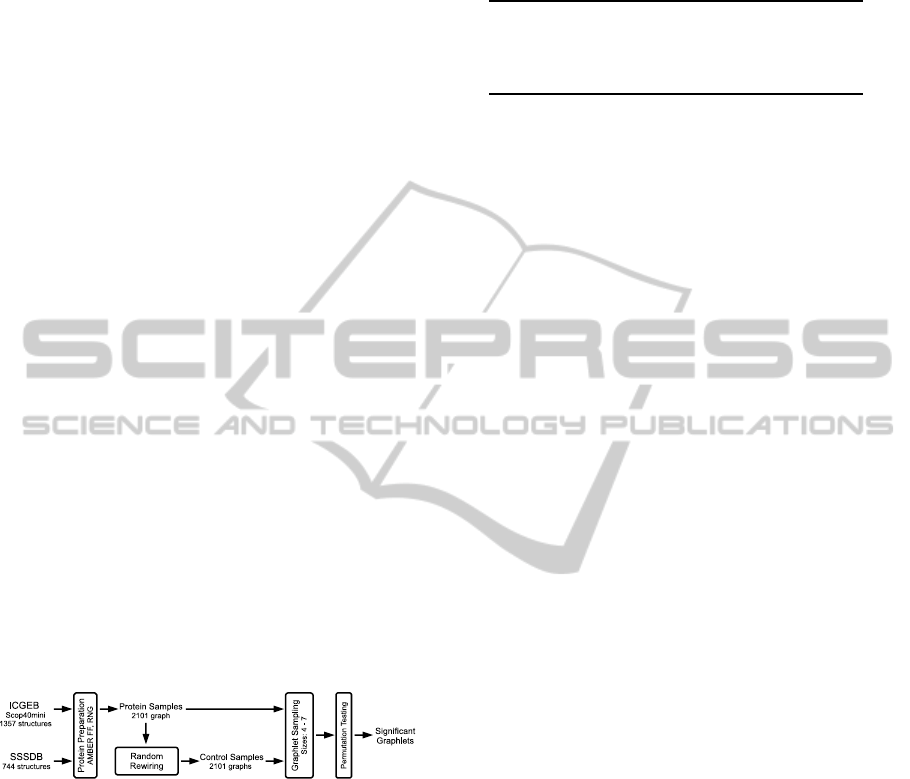
analysis. Figure 1 illustrates this analysis step.

Figure 1: The graphlet analysis workﬂow using a random

control and permutation testing.

Decision Tree Analysis

Here, we relate the extracted graphlets to global pro-

tein structure properties, e.g. the SCOP classiﬁca-

tion of each structure. Therefore, we employ decision

trees as they facilitate a better understanding of the

data set. Inspection of leafs and their associated sam-

ples allows relating speciﬁc graphlets to proteins and,

thus, facilitates the analysis of structures with respect

to interaction patterns. In addition, decision trees are

native multi-class prediction algorithms and are thus

a convenient choice for the prediction of various pro-

tein classes. However, decision trees tend to overﬁt

and therefore require careful complexity regulariza-

Table 1: Results of the Graphlet Analysis.

Graphlet Found Signiﬁcant Filter

Size Graphlets Graphlets Ratio

4 427 22 0.05

5 1,731 77 0.04

6 5,366 212 0.04

7 16,904 316 0.02

tion.

An alternative to decision trees are neural network

predictors. Neural networks represent a non-linear

class of regression functions that are estimated by gra-

dient descent. For each class a single output neu-

ron can be integrated into the network and, thus, a

single neural network can model the posterior proba-

bility of each class using a common basis of hidden

neurons. However, neural networks are pure highly

non-linear prediction models and, therefore, hard to

interpret. Consequently, they are less suited for data

mining purposes and do not provide much insight into

the dataset.

Using the graphlet distributions, we encode each

protein as a binary vector of graphlet occurrences.

Whenever a graphlet is found for a protein, it is en-

coded as 1 and as 0 else. In addition, we integrate the

SCOP level information from ICGEB as well as the

SSSDB Motif class information as a prediction target.

SCOP has four hierarchical levels: the class, fold, su-

perfamily and family of a protein domain. Similarly,

the SSSDB Motif Class encodes the super-secondary

structure super class, while the SSSDB Motif Sub-

class denotes a more precise subdivision.

We use the

partition

platform from

JMP

(SAS

Institute Inc., 2009) for learning. JMP is a reduced

version of the SAS Enterprise Miner software suite,

which is extensively used for professional data anal-

ysis in industry, and provides various platforms that

facilitate data analysis tasks. Especially, the ability of

the

partition

platform to easily inspect each predic-

tion node is helpful during the analysis of the inferred

graphlets. In our experiments, the Minimum Split

Size (MSS) parameter is chosen to be 5, 10, 15, 20, 25

and 50, while training on graphlets of size 4 to 7. For

each model, the prediction performance is evaluated

using 5-fold cross-validation to compute AUC values

for each class. Then, all AUC values are averaged to

yield the mean AUC (mAUC) for each combination

of graphlet size and MSS. For comparison purposes,

we also employ the

neural nets

platform.

Regularization

However, to obtain regularized decision trees, we fol-

low the work of (Scott and Nowak, 2005). There, the

ICFC 2010 - International Conference on Fuzzy Computation

192

space of decision tree hypotheses is regularized by

their number of leafs and their prediction error. Let T

be the hypothesis space of decision trees and |T| de-

note the number of leafs of a tree T. Furthermore, let

n be the number of data samples and λ be a weighting

factor between tree complexity and prediction error,

then the Complexity Regularization CR for decision

tree selection is given as

CR = argmin











|{z}

Empirical risk

+λ

|T|

|{z}

Bound on bias











(3)

where

R denotes the prediction error and n the num-

ber of training samples. In our case, we set

R =

1 − mAUC, because we are dealing with multi-class

predictions and the mAUC is a performance measure

between 0 and 1 that can be converted into an error

by subtracting it from 1. This error is then compared

to its theoretical bound, the Uniform Deviation Bound

UDB

, which upper bounds the true risk of a decision

tree and is given as

UDB

= argmin

T∈T

(

R(T) +

3|T| + log(n)

)

. (4)

The remaining task is to ﬁnd a valid λ for regular-

ization. We choose λ to minimize

λ = argmin

∑

(CR −UDB

)

(5)

for all considered decision trees, trained with MSS of

5, 10, 15, 20, 25, and 50.

3 RESULTS & DISCUSSION

Graphlet Extraction

We convert 1357 proteins from the ICGEB

SCOP40mini database and 744 proteins from

the SSSDB into the described graphical representa-

tion. Figure 2 illustrates the result of a conversion.

This results in a total of 2101 graphs left for graphlet

analysis. Two other datasets from ICGEB, PCB00020

(11,944 structures from SCOP95) and PCB00026

(11,373 structures from CATH95), are convenient for

our experiments. However, the enormous number of

graphlets found in this data sets leads to infeasible

computation times. Therefore, we restrict our analy-

sis to the smallest ICGEB collection and included the

SSSDB instead.

Table 1 summarizes our sampling results. It

shows that increasing the graphlet pattern size also

Figure 2: Structure (left) and RNG (right) of ICGEB struc-

ture

d1pmma

. Box nodes denote β-sheets, whereas round

nodes refer to α-helices.

increases the number of detected graphlets as well

as the number of signiﬁcant graphlets. However, the

ratio between signiﬁcant and detected graphlets re-

mains below 5%. Hence, we extract only a small

amount of signiﬁcant patterns from a large collection

of graphlets (see Table 1).

Decision Tree Learning

For each target variable the decision tree minimizing

CR −UDB

is selected as the regularized model and

saved for ﬁnal analysis. We ﬁnd that λ = 1.3 fulﬁlls

equation (5) for each target variable. We choose λ

such that the total squared deviation from the UDB

was minimal when averaged over all models using

any size of graphlets and any number of splits. Conse-

quently, all models are regularized and have maximal

expressive power along with a reduced probability of

overﬁtting. Table 2 lists the MSS, graphlet size, num-

ber of splits, as well as the mAUC of the ﬁnal models

for each target variable. We ﬁnd that simple models

sufﬁce to achievemAUC better than 0.82. In addition,

at least 20 samples can be summarized in a leaf to re-

sult in a decision tree predicting one category without

sacriﬁcing prediction performance. Finally, we ﬁnd

that graphlets of size 5 are in most cases superior to

others. Also graphlets of size 4 and 7 are used for

decision tree learning and, therefore, provide useful

information (Table 2).

We also compare the performance of decision

trees to the performance of neural networks, also im-

plemented in JMP. The last column of Table 2 shows

the mean AUC achieved by the

neural nets

plat-

form using cross-validation on a random selection of

40% of the samples, which are held out as external

validation set. The platform was trained using the de-

fault values. We ﬁnd that the neural network is supe-

rior to our regularized decision trees in predicting the

SCOP class and SCOP family, as well as the SSSDB

Motif Class. However, the performance difference

does not exceed a value of 0.06 mAUC points. Con-

GRAPHLET DATA MINING OF ENERGETICAL INTERACTION PATTERNS IN PROTEIN 3D STRUCTURES

193

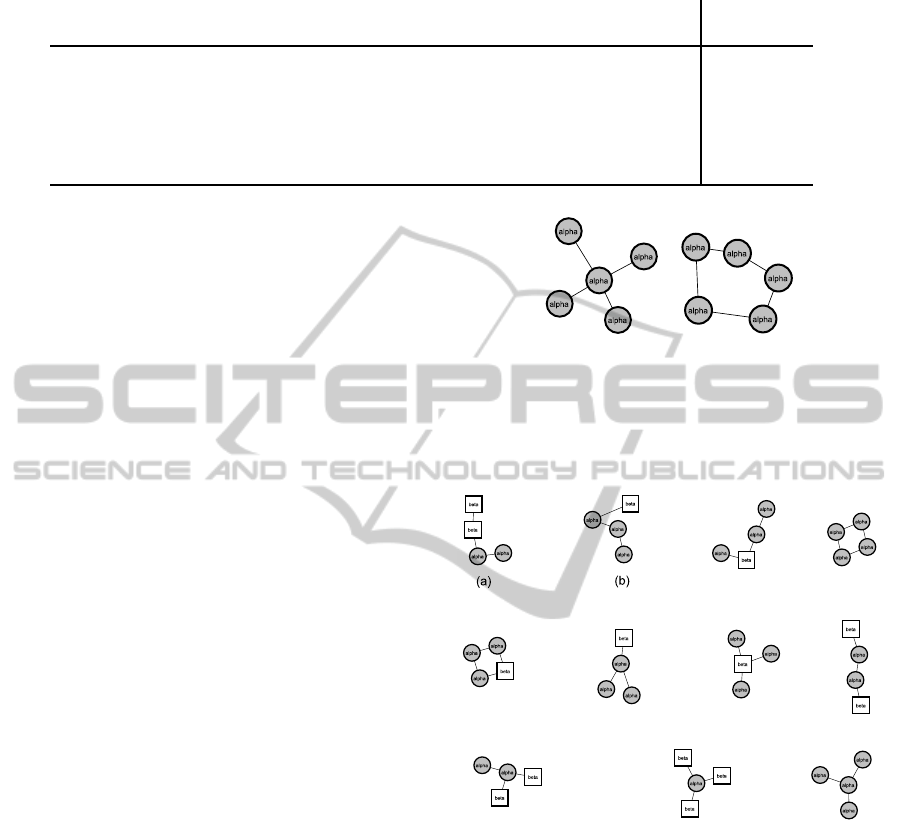
Table 2: Regularized Decision Trees for each target variable.

Target Variable # classes Graphlet MSS Performed mAUC Neural Net

Size Splits mAUC

SCOP class 5 5 20 23 0.87 0.92

SCOP fold 19 5 20 24 0.87 0.84

SCOP superfamily 7 4 20 24 0.85 0.83

SCOP family 48 5 20 16 0.83 0.87

SSSDB Motif Class 32 7 10 22 0.93 0.99

SSSDB Motif Subclass 153 5 15 21 0.96 0.96

sequently, decision trees and neural networks achieve

a comparable performance and, therefore, support the

descriptive value of our graphlet features.

Next, we extract all graphlets from the selected

regularized decision tree models to analyse their us-

ages with respect to all target variables. Here, we ﬁnd

graphlets that are used several times for the predic-

tion of various target variables, while other graphlets

are speciﬁc to one class.

While 66 graphlets are used only for the prediction

of one target variable, we ﬁnd two graphlets of size

5 that are used to predict 4 different target variables

(Figure 3). Note that this is the maximum number

achievable because two target variables are predicted

using graphlets of size 4 and 7.

In Figure 4 all SCOP superfamily graphlets are

shown. Within the decision tree for the SCOP super-

family, the graphlets (a) and (b) in Figure 4 are more

relevant for classiﬁcation, because they are used in

three and two splits, respectively. Interestingly, (a)

and (b) are paths of helices containing one or two

sheets, while the other graphlets consist mainly of star

topologies.

Finally, we predict all detected graphlets from sec-

ondary structure sequence. Therefore, we convert

each protein sequence into strings of symbols h,s, l

encoding whether a residue is within a helix, strand

or loop. We design a set of 439 features describing

lengths, as well as densities, normalized to protein

length, of helices, strands, loops. In addition, we de-

sign regular expressions for SSE sequence patterns,

which result in binary features. Then, we train deci-

sion trees, implemented in the

rpart

package of

and use 5-fold cross-validation using the

bootstrap

package to estimate the MCC (Baldi et al., 2000). We

ﬁnd that chains of SSEs and star topologies can be

best predicted by decision trees.

4 CONCLUSIONS

In summary, we ﬁnd that signiﬁcantly overrepre-

sented patterns in energetic SSE interactions exist and

(a) (b)

Figure 3: Graphlet 3(a) predicts 4 targets and is predictable

with MCC=0.6, while graphlet 3(b) predicts 4 targets and is

predictable with MCC=0.5 from secondary-structure infor-

mation.

Figure 4: This ﬁgure shows all extracted graphlets used for

the prediction of the SCOP superfamily.

can be found using graphlet analysis. Regularized

decision tree learning on the mined patterns predicts

SCOP levels and SSSDB Motifs with great accuracy

(mAUC > 0.8) using about 20 graphlets. Also, the

presence of a speciﬁc graphlet can be predicted from

secondary structure sequence of a protein with MCC

values up to 0.7. Finally, we demonstrate that the

combination of graphlet analysis using permutation

testing and decision tree learning facilitates automatic

categorization of protein structures.

We have shown that graphlets are predictable from

the secondary structure sequence, therefore graphlets

can be used as constraints for the placement of pre-

dicted secondary structure elements, when predict-

ICFC 2010 - International Conference on Fuzzy Computation

194

ing the tertiary structure from the protein sequence

alone. Thus, future work should focus on the usage of

the predictable graphlets to improve ab initio protein

structure prediction.

REFERENCES

Baldi, P., Brunak, S., Chauvin, Y., Andersen, C. A. F., and

Nielsen, H. (2000). Assessing the accuracy of predic-

tion algorithms for classiﬁcation: an overview. Bioin-

formatics, 16(5):412–424.

Chiang, Y.-S., Gelfand, T. I., Kister, A. E., and Gelfand,

I. M. (2007). New classiﬁcation of supersecondary

structures of sandwich-like proteins uncovers strict

patterns of strand assemblage. Proteins, 68(4):915–

921.

Georgii, H.-O. (2004). Stochastik. de Gruyter, 2nd edition.

p.198.

Holm, S. (1979). A simple sequentially rejective multi-

ple test procedure. Scandinavian Journal of Statistics,

6(2):65–70.

Kabsch, W. and Sander, C. (1983). Dictionary of protein

secondary structure: Pattern recognition of hydrogen-

bonded and geometrical features. Biopolymers,

22(12):2577–2637.

Kohlbacher, O. and Lenhof, H.-P. (2000). BALL–rapid soft-

ware prototyping in computational molecular biology.

Bioinformatics, 16(9):815–824.

Milligan, G. W. and Isaac, P. D. (1980). The validation of

four ultrametric clustering algorithms. Pattern Recog-

nition, 12(2):41 – 50.

Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N.,

Chklovskii, D., and Alon, U. (2002). Network Mo-

tifs: Simple Building Blocks of Complex Networks.

Science, 298(5594):824–827.

Murzin, A. G., Brenner, S. E., Hubbard, T., and Chothia,

C. (1995). Scop: A structural classiﬁcation of pro-

teins database for the investigation of sequences and

structures. Journal of Molecular Biology, 247(4):536

– 540.

Orengo, C. A., Michie, A. D., Jones, S., Jones, D. T.,

Swindells, M. B., and Thornton, J. M. (1997). CATH–

a hierarchic classiﬁcation of protein domain struc-

tures. Structure, 5(8):1093–1108.

R Development Core Team (2009). R: A Language and

Environment for Statistical Computing. R Foundation

for Statistical Computing, Vienna, Austria. ISBN 3-

900051-07-0.

SAS Institute Inc. (2009). Jmp 8.0.1. www.jmp.com.

Scott, C. and Nowak, R. (2005). On the adaptive properties

of decision trees. In Advances in Neural Information

Processing Systems 17. MIT Press.

Sonego, P., Pacurar, M., Dhir, S., Kertesz-Farkas, A., Koc-

sor, A., Gaspari, Z., Leunissen, J. A. M., and Pon-

gor, S. (2007). A Protein Classiﬁcation Benchmark

collection for machine learning. Nucleic Acids Res,

35(Database issue):D232–D236.

Toussaint, T., G. (1980). The relative neighbourhood graph

of a ﬁnite planar set. Pattern Recognition, 12:261 –

268.

Vacic, V., Iakuoucheva, L., Lonardi, S., and Radivojac, P.

(2010). Graphlet kernels for prediction of functional

residues in protein structures. Journal of Computa-

tional Biology, 17(1):55 – 72.

Wald, A. and Wolfowitz, J. (1944). Statistical tests based

on permutations of the observations. The Annals of

Mathematical Statistics, 15(4):358–372.

Wassermann, L. (2004). All of statistics. Springer. theorem

14.5.

GRAPHLET DATA MINING OF ENERGETICAL INTERACTION PATTERNS IN PROTEIN 3D STRUCTURES

195