OPTIMIZING GENETIC ALGORITHM PARAMETERS FOR A

STOCHASTIC GAME

James Glenn

Department of Computer Science, Loyola University Maryland, 4501 N. Charles Street, Baltimore, Maryland, U.S.A.

Keywords:

Genetic algorithm, Parameter optimization, Stochastic games, Heuristics.

Abstract:

Can’t Stop is a jeopardy stochastic game played on an octagonal game board with four six-sided dice. Pre-

vious work generalized a well-known heuristic strategy for the solitaire game and attempted to optimize the

parameters of the generalized strategy using a genetic algorithm (GA). There were two challenges in that

optimization process: ﬁrst, the stochastic nature of the game results in a very noisy ﬁtness function; second,

the ﬁtness function is computationally expensive. In this work we continue the optimization process for the

heuristic strategy by optimizing the GA: for a ﬁxed number of ﬁtness function evaluations, we investigate the

effects of varying the GA parameters (in particular the population size and number of generations), which in

turn affect the number of samples per individual and thus noise as well. We also examine different sampling

schedules; our schedules are unique in that selecting the ﬁnal champion is considered a schedulable phase.

The GA parameters are ﬁrst optimized on an easy-to-compute test function. The resulting GA parameters are

effective on the original problem and as a result we obtain an improved heuristic strategy for Can’t Stop.

1 INTRODUCTION

Can’t Stop is a board game for two to four players

with elements of both strategy and chance (Sackson,

2007). Simpliﬁed versions of Can’t Stop (includ-

ing solitaire versions) have been solved (Glenn et al.,

2008), but the original game is difﬁcult to solve be-

cause of the large number of states that must be evalu-

ated. Keller (1986) developed a heuristic strategy that

Glenn and Aloi later generalized into a parameterized

strategy for solitaire Can’t Stop, where the parameters

were selected with a genetic algorithm (GA) (Glenn

and Aloi, 2009); the ﬁtness of a set of parameters

was the average number of turns needed to complete

the game using the corresponding strategy. That ﬁt-

ness function was estimated by repeated simulations

of game play. Because the amount of time needed to

simulate a game is nontrivial, it is not feasible to sim-

ply run the GA until the population stops improving;

it is more practical to limit the number of simulations

performed during each run of the GA. However, be-

cause of the noisy nature of the estimated ﬁtness func-

tion, the GA is sensitive to its parameters, particularly

the population size and number of generations, and

to the scheduling of the evaluations (studied in a dif-

ferent domain by Aizawa and Wah (1993)), which to-

gether will determine the number of simulations per-

formed for a particular set of strategy parameters.

In this work we ﬁrst optimize the GA parame-

ters by substituting an easy-to-compute test function.

We consider primarily population size, number of

generations, Aizawa and Wah’s “between-generations

scheduling”, and a new aspect of scheduling we call

“phase scheduling”. We obtain better parameters for

the generalized solitaire Can’t Stop strategy by opti-

mizing them with the resulting GA.

2 RULES OF CAN’T STOP

Can’t Stop was invented by Sid Sackson and orig-

inally published by Parker Brothers in 1980 (it is

currently published by Face 2 Face Games (Sack-

son, 2007)). Can’t Stop is one of a class of games

called jeopardy stochastic games (or, more speciﬁ-

cally, jeopardy dice games when the stochastic ele-

ment is supplied by dice) in which each player’s turn

is a sequence of stochastic events, some of which al-

low the player to make progress towards a goal, and

some of which will end the player’s turn immediately.

After each incremental step towards the goal, play-

ers can choose to end their turn, in which case the

progressmade during the turn is banked and cannot be

lost on a later turn. Players who press their luck and

199

Glenn J..

OPTIMIZING GENETIC ALGORITHM PARAMETERS FOR A STOCHASTIC GAME.

DOI: 10.5220/0003079101990206

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 199-206

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: A Can’t Stop position. Black squares represent

the colored markers; gray squares are the neutral markers.

choose to continue their turns risk being forced to end

their turns by an adverse outcome of the stochastic

event (for example, rolling a one), in which case they

lose any progress made during the turn. Pig (solved

for two players (Neller and Presser, 2004; Neller and

Presser, 2006)), Ten Thousand, and Cosmic Wimpout

are other examples of jeopardy stochastic games.

The speciﬁc rules for Can’t Stop are as follows.

The game board has columns labelled 2 through 12

(the totals possible on two dice). Columns 2 and 12

are three spaces long, 3 and 11 are ﬁve spaces long,

and so forth to the thirteen spaces in column 7. Each

player has one marker for each column, colored to

distinguish them from other players’ markers. There

are three neutral markers (white) that are used to mark

progress during a turn. Each turn follows these steps:

(1) the current player rolls four six-sided dice;

(2) the player groups the dice into two pairs in such a

way that progress can be made in the next step – if

that is impossible then the turn ends immediately

with the neutral markers removed from the board

and the colored markers left as they are;

(3) in each column for the pair totals, either a new

neutral marker is placed one space above the

player’s colored marker or the neutral marker is

advanced one space, depending on whether there

was already a neutral marker in the column;

(4) the player chooses between returning to step (1) or

ending the turn, in which case the player’s colored

markers advance to replace the neutral markers.

The goal of the game is to be the ﬁrst player to ad-

vance to the top of any three columns (or to do so in as

few turns as possible for the solitaire version). Once a

player wins a column then no player can make further

progress in that column. The player must use both

pair totals if possible, but is allowed to choose which

to use if the pairing in step (2) results in pairs such

that one or the other can be used, but not both at the

same time (this can happen if only one neutral marker

remains). (Note that there is ambiguity in the ofﬁcial

rules: we interpret the rule “if you can place a marker

on your roll, you must” so it applies after a player has

chosen how to pair the dice.)

For example, in Figure 1 the possible pair totals

would be 4 and 10 or 6 and 8. In the former case the

neutral markers would be moved ahead one space in

columns 4 and 10. In the latter case the marker in col-

umn 6 would be moved up one space but no progress

would be made in column 8 because all three neutral

markers have been used. If the roll had been 6-6-6-6

then the player would have lost all progress because

the only possible pair totals would be two 12s, but

column 12 has been won and so is out of play.

3 VALUE ITERATION AND

NEWTON’S METHOD

Retrograde analysis is a common bottom-up tech-

nique used to compute game-theoretic values of

positions by starting with the terminal positions

and working backwards towards the starting posi-

tion (Str¨ohlein, 1970). For acyclic games, retrograde

analysis simply evaluates positions in reverse topo-

logical order. This technique has been used to solve

solitaire Yahtzee (Woodward, 2003; Glenn, 2006).

Retrograde analysis in its more complexforms has

been applied to endgames for non-stochastic games

including chess (Thompson, 1986; Thompson, 1996),

checkers (Lake et al., 1994; Schaeffer et al., 2004),

and Chinese chess (Wu and Beal, 2001; Fang, 2005a;

Fang, 2005b), and has been used to solve Nine Men’s

Morris (Gasser, 1996), Kalah (Irving et al., 2000), and

Awari (Romein and Bal, 2003).

The cyclic and stochastic nature of Can’t Stop re-

quires a different approach. The cycles arise from the

fact that a turn can end with no progress made. Value

iteration is one approach to handling the cycles (Bell-

man, 1957). The value iteration algorithm starts with

estimates of the position values of each vertex. Each

vertex’s position value is then updated (in no particu-

lar order in the most general form) based on the es-

timates of its successor’s values to yield a new es-

timated value. In this way the estimates are reﬁned

until they converge.

Because the cycles in Can’t Stop are only one

turn long (progress that has been banked can never be

lost), the game graph can be decomposed into com-

ponents, each of which component consists of an an-

chor representing the start of a turn and all of the

positions that can be reached before the end of that

ICEC 2010 - International Conference on Evolutionary Computation

200

turn. The components form an acyclic graph and

can be processed in reverse topological order. Iter-

ative methods can then be used within the compo-

nents; one method (Glenn et al., 2008) breaks the

cycles within the components by removing anchors’

incoming edges, guesses a position value x for the an-

chor, and then computes a new estimate f(x) of the

anchor’s position value. The resulting function f is

continuous and piecewise linear; the ﬁxed point of f

gives the position value of the anchor. For any x, f(x)

and f

′

(x) can be computed using retrograde analy-

sis within the component. Computing f

′

(x) allows

the use of Newton’s method, which converges to the

ﬁxed point signiﬁcantly faster than value iteration or

its variants.

4 HEURISTIC STRATEGIES

The method described above has been used to solve

simpliﬁed variants of solitaire Can’t Stop. These vari-

ants use dice with fewer than six-sides and a board

with possibly shorter columns. The variants are re-

ferred to as (n, k) Can’t Stop where n is the number

of sides on the dice and k is the length of the shortest

column (with adjacent columns always differing by 2

in length).

The most complex version of solitaire Can’t Stop

that has been solved is (5, 2) Can’t Stop. Evaluating

its 17 billion positions took 60 CPU days; an estimate

for the time required to solve the ofﬁcial game us-

ing current techniques is 3000 CPU years. Heuristic

strategies for the full game are therefore still of inter-

est. Even for simple games heuristics are more useful

to human players: no human can memorize the data or

mentally perform the calculations needed to replicate

the optimal strategy for (5,2) Can’t Stop.

4.1 The Rule of 28

One heuristic strategy is the Rule of 28 (Keller, 1986).

The Rule of 28 is used to determine when to end a turn

by assigning a progress value to each conﬁguration

of the neutral markers. Players should end their turn

when this value reaches or exceeds 28. The progress

value computation is split into two parts: one part for

measuring the progress of the neutral markers; and

one part for assessing the difﬁculty of making a roll

that will allow further progress.

The ﬁrst part of the progress value is computed

as column-by-column sum. The value a column con-

tributes to the sum is computed as some constant

weight assigned to that column times one more than

the number of spaces advanced in that column. The

weights are one for column 7, two for columns 6 and

8, and so forth to six for columns 2 and 12, reﬂect-

ing the fact that it is more difﬁcult to make progress

in the outer columns, and those columns are shorter,

so progress in them is therefore more valuable. So

if ~s = (s

,. .. , s

) where s

is the number of spaces

of progress in column i during the current move, then

the marker progress value is

(~s) =

∑

i=2

+ 1)(|7−i|+ 1). (1)

Because certain combinations of columns are

riskier to be in than others, a difﬁculty score is added

to that sum. For example, if a roll is all evens then it is

impossible to make an odd pair total. Therefore, two

points are added to the progress value when all three

neutral markers are in odd columns. On the other

hand, every roll permits at least one even pair total,

so if the neutral markers are all in even columns, two

points are subtracted from the progress value, length-

ening a turn. Additionally,four points are added when

the columns are all high (≥ 7) or all low (≤7).

For example, in Figure 1 the progress value for

column 4 is (2 + 1) ·4 = 12, the progress value for

column 6 is (3+ 1) ·2 = 8, and the progress value for

column 10 is (1+ 1) ·4 = 8. Because all three neutral

markers are in even columns, 2 points are subtracted

to get a total progress value of 12+ 8 + 8 −2 = 26.

The Rule of 28 suggests rolling again.

A similar scheme can be used to determine how

to pair the dice: each column is assigned a weight and

each possible move is scored according to the weights

of the columns it would make progress in. The to-

tal is called the move value; the move with the high-

est move value is the one chosen. Giving the outer

columns lower weights than the middle columns (thus

favoring choosing the middle columns) works better

than the opposite pattern. In order to conserve neu-

tral markers, a penalty is subtracted for each neutral

marker used. In particular, if ~p = (p

,. .. , p

) where

is the number of squares advanced by a move in

column i and ~m = (m

,. .. , m

) where m

is 1 if the

move places a new neutral marker in column i and 0

otherwise, then the total move value is

(~p, ~m) =

∑

c=2

·(6−|7−i|) −6·m

) (2)

For example, in Figure 1 using the 6 has a score of 5

(the move value of one space in column 6). Using the

4 and 10 has a score of 3+ 3 = 6, so this rule suggests

using the 4 and 10.

When we henceforth refer to the Rule of 28 we

mean the Rule of 28 combined with the above method

OPTIMIZING GENETIC ALGORITHM PARAMETERS FOR A STOCHASTIC GAME

201

of choosing how to pair the dice. This strategy av-

erages approximately 10.74 turns to win the solitaire

game.

4.2 Generalizing the Rule of 28

Any of the constants assigned to the columns can

be altered, as can the threshold and any of the difﬁ-

culty values. Furthermore, the spaces within a column

needn’t be assigned the same weights. In general, to

evaluate a particular move we denote the move by two

vectors ~m = (m

,. .. , m

) and~n = (n

,. .. n

) where

is the position of the neutral marker in column i (or

the colored marker if there is no neutral marker) be-

fore the move and n

is the position the neutral marker

would advance to after the move. Assign the weight

to space j in column i. Then the total move value

v is the sum of the weight of the spaces that would

be advanced over in the current turn if that move was

made:

(~m,~n) =

∑

i=2

∑

j=m

. (3)

The same technique could be applied to progress val-

ues as well.

4.3 Linear Weights Strategies

Previous work studied two constrained versions of the

generalized heuristic (Glenn and Aloi, 2009). The

most ﬂexible (and most successful) constrained the

progress values to be constant within each column

and required the move weights x

to be described

by a linear function within each column. Specif-

ically, a Linear Weights strategy was described by

,. .. , p

,..., m

,..., b

,e, o,h,k,t) where

1. the p

are progress values with p

∈ {0, .. .7} for

each column i ∈ {2, .. ., 7} (symmetry is used so

that, for example, p

= p

2. m

and b

deﬁne the linear function for column i

that determines the move weights of each space

within that column:



+ b



(4)

(where l

is the length of column i, m

is chosen

from 32 somewhat arbitrarily chosen values be-

tween 0 and 64, and b

∈ {0,. .. ,7}),

3. e, o, and h are the even, odd, and high penalties

(each chosen from between -8 to 7 and with the

low penalty l equal to the high penalty h),

4. k is the marker penalty (between 0 and 15), and

5. t is the progress threshold (between 0 and 31).

The best Linear Weights strategy found achieved

an average score of 9.05 turns, with a standard devia-

tion of 2.30.

5 GENETIC ALGORITHM

The parameters of the Linear Weights strategies

have been optimized using a genetic algorithm

(GA) (Glenn and Aloi, 2009). Each candidate strat-

egy was encoded using the appropriate number of bits

for each parameter (87 total). Various-sized popula-

tions of those bit strings were subjected to standard

GA operators (two-point crossover, mutation, two-

round tournament selection) for twenty generations.

The ﬁtness of an individual strategy was taken to be

the expected number of turns that strategy takes to ﬁn-

ish the solitaire game. That expectation was estimated

by computing the mean over n simulated games. The

high level of noise in the evaluation function (the best

strategy found has a standard deviation of approxi-

mately 25% of its mean turns to complete the game)

was therefore an issue. Some attempt was made to de-

termine the optimal population size for a ﬁxed number

of total evaluations, but the results were not conclu-

sive. We now strive to better optimize the parameters

of the Linear Weights strategies; to do so we will ﬁrst

optimize the GA parameters. We continue with a GA

instead of some other optimization method for two

reasons:

1. the ﬁtness function is multi-modal; and

2. Arnold and Beyer (2003) found that in a simple

environment with high levels of noise, evolution

strategies were more robust than other optimiza-

tion algorithms, and we assume that this robust-

ness is shared with genetic algorithms.

5.1 Optimizing Genetic Algorithm

Parameters in the Presence of Noise

For a ﬁxed number of total simulations there is a

tradeoff between using more evaluations per individ-

ual (thus reducing noise) and having a larger popu-

lation (increasing diversity and allowing more of the

search space to be examined). Fitzpatrick and Gref-

fenstette (1988) performed analysis suggesting that in

noisy environments and given a ﬁxed number of func-

tion evaluations, it is better to have a larger popula-

tion with fewer evaluations than a smaller population

with more evaluations. They then presented empiri-

cal work with two problems (a noisy version of one

of De Jong’s (1975) original test functions, and medi-

cal image registration) that conﬁrmed their analysis to

ICEC 2010 - International Conference on Evolutionary Computation

202

a point: choosing a population size that allowed two

evaluations per individual was generally better than

choosing a population size that allowed only one eval-

uation. They used a ﬁxed number of generations, ex-

cept that they reduced the number of generations in

cases where it was necessary to compensate for the

additional GA overhead required for larger popula-

tions (that is, when the GA overhead was not domi-

nated by the total evaluation time).

Arnold and Beyer (2003) found that for low levels

of noise, efﬁciencydrops as population size increases.

These two results together suggest that there is an op-

timal population size that is reached once noise is

reduced sufﬁciently. Experiments with the solitaire

version of the game Yahtzee (Glenn, 2007) presented

some conﬁrmation of that, although the value exam-

ined was the average ﬁtness in the ﬁnal generation

rather than the best individual.

Aizawa and Wah (1993) considered the schedul-

ing of a ﬁxed number of evaluations for a ﬁxed pop-

ulation size in two senses: “duration scheduling” or

“between-generation scheduling”, which determines

how many evaluations are used during each genera-

tion; and “sample allocation” or “within-generation

scheduling”, which determines how many evaluations

are allocated to each member of a population within

a single generation. They found that performance im-

proves when more evaluations are scheduled in later

generations, and that a dynamic approach to within-

generation scheduling offers further improvements.

Jin and Branke (2005) survey more approaches to

dealing with noise.

We now wish to consider more completely the ef-

fects of GA parameters on the results with the aim

of further optimizing the Linear Weights strategies.

However, since a single run of the GA can take sev-

eral hours, it is computationally expensive to do so

by trial and error (or by using a meta-GA). Instead,

we optimize the GA parameters for a function that is

easier to compute and then hope it has characteristics

similar enough to those of the ﬁtness function for the

Linear Weights strategies so that the same GA param-

eters will work well for the latter.

5.2 Schwefel’s Function

The function we choose to model noise is Schwefel’s

function, a well-known function used to benchmark

genetic algorithms (M¨uhlenbein et al., 1991; T¨orn

and Zilinskas, 1989). Schwefel’s function takes n real

numbers as inputs and is deﬁned by

s(x

,..., x

) =

∑

i=1

420.9697−x

·sin

| x

|. (5)

Schwefel’s function is continuous and highly multi-

modal; those properties along with the fact that it can

be extended to any number of inputs makes it a desir-

able test case. We deﬁne a family of functions equal

to Schwefel’s function with noise introduced: let s

′

n,σ

be deﬁned by

′

n,σ

,..., x

) = s(x

,..., x

) +

(0;σ), (6)

where the last term denotes a random variable with

the given normal distribution. This variable is chosen

anew each time s

′

n,σ

is evaluated.

When the inputs are restricted to [−500, 500],

Schwefel’s function is minimized to zero when all

inputs x

are equal to 420.9697.. . (which is near a

boundary and far from the next-best local minima,

which occur when x

= −302.5249.. . for one i and all

other x

equal 420.9697. ..). In the absence of noise

there are methods that have no trouble ﬁnding this

minimum. We wish to determine, for different noise

levels, the optimal parameters for a GA that uses a

ﬁxed number of evaluations of s

′

n,σ

. We will inves-

tigate how those parameters depend on n and σ, and

how effective the resulting GA is.

5.3 Selecting GA Parameters

We now consider optimizing the following genetic al-

gorithm parameters: 1) the population size; 2) the

number of generations; 3) the between-generations

schedule, simpliﬁed so the number of evaluations

used during a particular generation is a linear function

of the generation number; and 4) the “phase sched-

ule”. The phase-scheduling problem is a third type

of scheduling problem we introduce to go along with

between- and within-generation scheduling. Our GA

is divided into two phases: the evolution phase, and

the ﬁnal champion selection phase. The latter phase

is necessary for two reasons: because the expected

number of evaluations per member of the population

will be very low, it is impossible to select the over-

all most ﬁt individual with any conﬁdence; and it is

currently infeasible to compute the exact ﬁtness of a

particular Linear Weights strategy. The latter compli-

cation is not present when dealing with test functions

with artiﬁcially introduced noise such as Schwefel’s

function or De Jong’s function (one can simply evalu-

ate the exact ﬁtness by not adding in the noise), and is

not present to the same extent when dealing with Fitz-

patrick and Greffenstette’s problem of medical image

registration (instead of estimating ﬁtness by using a

sample of pixels, one can compute the exact ﬁtness by

examining every pixel; there is additional overhead,

but that overhead can be accounted for).

We therefore add a second phase to the GA after

the ﬁnal generation has been generated. In this phase

OPTIMIZING GENETIC ALGORITHM PARAMETERS FOR A STOCHASTIC GAME

203

we use many more evaluations in order to greatly im-

prove our ﬁtness estimates so we can determine with

some conﬁdence the overall most ﬁt individual (the

“ﬁnal champion”) from among some pool of candi-

dates, which we take to be the entire ﬁnal generation.

We use a constant mutation rate and crossover rate

and do not consider the effects of dynamic within-

generation scheduling, although we do use a some-

what simpliﬁed version of dynamic scheduling in the

ﬁnal champion selection phase.

Results of a meta-GA used to determine optimal

parameters for a GA optimizing s

′

,. .. , x

,1000)

indicated that evaluation scheduling is less important

than the population size and number of generations –

the meta-GA tended to settle on the same values for

population size and number of generations but chose

wider ranges for the other parameters over several

runs. We therefore examined the former two param-

eters more closely. We varied the number of gener-

ations between 32 and 1024 and the population size

between 64 and 2048. We ran a GA with those pa-

rameters to optimize s

′

n,σ

. Each run of the GA used

2,500,000 total ﬁtness evaluations, the same number

of evaluations for each generation, and 16% of evalu-

ations to select the ﬁnal champion. Sixteen bits were

used to represent each input to s

′

(n). The mean ﬁt-

ness of the ﬁnal champion over 100 runs of the GA

for s

′

10,1000

, s

′

10,4000

, and s

′

20,1000

are given in Tables

1-3. Values that are statistically signiﬁcantly different

than the minimum (boxed) at the p = 0.05 level are

given in bold.

Table 1: Average ﬁtness of champions for s

′

10,1000

Population

Gen. 128 256 512 1024 2048

32 190.3 99.02 72.21 69.31 70.71

64 151.4 58.24 46.06 50.75 54.89

128 125.3 48.54 40.79 45.92 50.05

256 134.1 44.77 40.30 46.39 52.69

512 149.0 50.74 41.48 45.73 57.61

1024 113.5 54.95 47.23 51.50 59.51

Table 2: Average ﬁtness of champion for s

′

10,4000

Population

Gen. 128 256 512 1024 2048

32 271.2 173.0 165.7 172.6 218.7

64 220.0 125.4 101.0 104.2 132.3

128 201.9 103.1 91.78 89.89 103.4

256 218.7 107.3 89.74 93.67 100.3

512 217.1 120.8 100.1 94.85 110.8

1024 240.4 138.5 109.7 105.1 114.8

Table 3: Average ﬁtness of champion for s

′

20,1000

Population

Gen. 128 256 512 1024 2048

32 1115. 685.3 491.7 394.2 338.7

64 667.4 311.3 165.1 139.6 138.4

128 560.1 222.2 112.7 103.4 113.4

256 496.6 206.2 100.1 101.7 114.4

512 475.7 202.3 106.6 106.1 119.2

1024 446.3 203.7 119.4 117.0 131.6

We can compare the performance of the GA in

the presence of noise to the results obtained by the

Breeder Genetic Algorithm (BGA) (M¨uhlenbein and

Schlierkamp-Voosen, 1993). In the absence of noise,

BGA was able to ﬁnd the minimum of the 20-input

version of Schwefel’s function using 16,100 func-

tion evaluations. We performed roughly 155 times

as many evaluations. Applying those evenly to the

16,100 inputs evaluated by BGA would reduce the

noise level for s

′

20,1000

to approximately

1000

√

155

≈ 80;

our GA on average found solutions about 1.25 stan-

dard deviations from the minimum.

The optimal parameters seem to be fairly insen-

sitive to the noise level and the number of inputs. If

anything, there is possibly a trend towards a larger

population as noise and number of inputs increase.

That is perhaps a counterintuitive notion since those

changes would result in fewer evaluations per indi-

vidual and one might expect that noise would be best

mitigated by increasing the number of evaluations per

individual.

6 TRANSFER TO CAN’T STOP

Guided by the results on the noisy version of Schwe-

fel’s function, we ran a GA to optimize the Linear

Weights strategies using a population of 512 individ-

uals evolved over 256 generations. We used 10

eval-

uations per execution of the GA, allocating an equal

number of evaluations to each generation and 16%

of the total to select the ﬁnal champion from the last

generation. Then, to check whether those parameters

were optimal for the Linear Weights strategies, we

reran the GA for populations of 128, 256, 512, and

1024 evolved over 64, 128, 256, and 512 generations.

We ran the GA up to 60 times for each combination of

parameters; the average ﬁtness of the ﬁnal champions

are given in Table 4.

We have also run the GA with different between-

generation schedules and different phase schedules

to conﬁrm that the parameters have the same (very

small) effect on the GA for the Linear Weights strate-

ICEC 2010 - International Conference on Evolutionary Computation

204

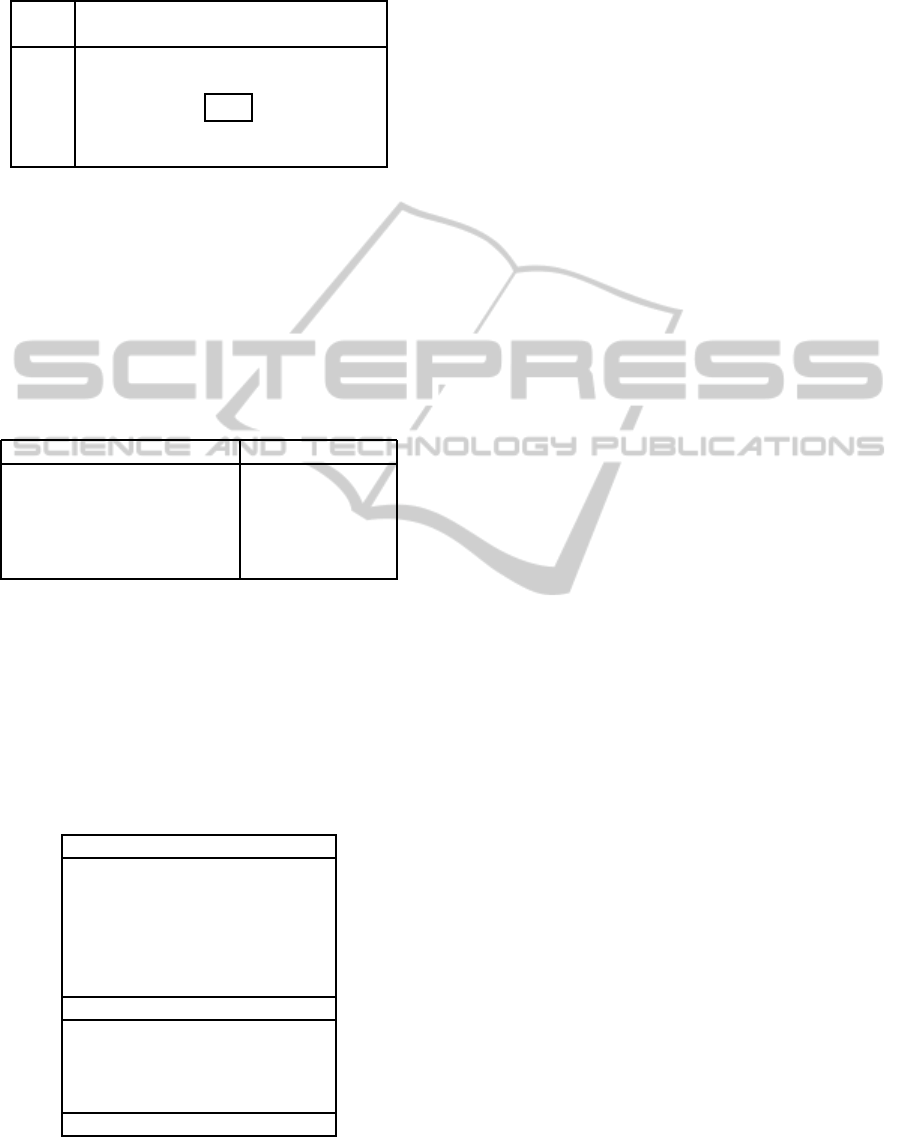
Table 4: Effects of GA parameters on linear weights cham-

pions.

Population

Gen. 64 128 256 512 1024

64 9.01 8.93 8.95 8.97 9.00

128 8.98 8.92 8.90 8.95 8.95

256 8.93 8.91 8.89 8.92 8.97

512 8.94 8.91 8.91 8.94 9.05

1024 8.96 8.92 8.95 9.01

gies that they do on the noisy Schwefel’s function.

Results are given in Table 5 and compared to the

standard of 256 generations, population 256, 16% of

evaluations to select the ﬁnal champion, and constant

between-generation schedule. Statistically signiﬁcant

differences are in bold; it seems that varying these pa-

rameters has as much effect as varying the population

size or number of generations by a factor of two.

Table 5: Effects of evaluation scheduling on linear weights

champions.

Variation Champion Mean

Standard 8.889

8% to select champion 8.897

32% to select champion 8.904

3x evaluations in ﬁrst gen. 8.913

3x evaluations in ﬁnal gen. 8.890

The best strategy found over all the runscompletes

solitaire Can’t Stop in an average of 8.78 turns (ver-

sus 9.05 for the best in the previous work by Glenn

and Aloi (2009)). It was found using a GA with

a population of 512 and 256 generations, and with

a between-generations schedule that allocated three

times as many evaluations to the ﬁnal generation as

to the ﬁrst. Its parameters are given in Table 6.

Table 6: Overall linear weights champion.

Column Progress Move

2,12 15 72x+ 15

3,11 13 48x

4,10 8 56x+ 3

5,9 8 44x

6,8 4 28x+ 7

7 3 32x+ 5

Difﬁculty Scores

odds 11

evens -1

highs, lows 4

marker 12

threshold 61

The encoding used here uses one more bit per pa-

rameter, thus allowing a wider range of values for

each. Furthermore, one bug has been ﬁxed since

Glenn and Aloi’s original implementation of the gen-

eralized heuristic. To isolate the effects of those

changes from the effects of the optimized GA param-

eters, we ran the GA with the changes in effect but

with the old, unoptimized GA parameters (population

400, 20 generations, but 25% more evaluations). The

average ﬁtness of the ﬁnal champion was 9.12 with a

best over 40 runs of 8.93. About half of the improve-

ment is therefore due to the more expressiveencoding

combined with the bug ﬁx and about half is due to the

optimized GA parameters.

6.1 Other Games

In a previous study (Glenn, 2007) we introduced a

class of strategies for solitaire Yahtzee that use an es-

timate of the expected score in each category to esti-

mate the position value at the start of each turn. We

optimized the estimates using 34 runs of a genetic al-

gorithm and found a strategy with an expected score

of 243.63. We reran the GA 40 times using the same

parameters as for Can’t Stop and found a strategy with

an expected score of 244.11, which closes 4.4% of the

gap to the optimal score of 254.59.

7 CONCLUSIONS

We have conﬁrmed previous results in other domains

suggesting that, in the presence of noise, there is some

fairly low optimal number of samples per individ-

ual. A key difference is the deﬁnition of “fairly low”:

Fitzpatrick and Greffenstette (1988) found the opti-

mal value to be 2; our results show a optimal value

between 10 and 20 for Schwefel’s function and the

parameterized Can’t Stop heuristic. It remains to be

determined what characteristics of the objective func-

tion and noise determine the optimal number of sam-

ples and other GA parameters.

Our study shows that optimal GA parameters for

the generalized heuristic and for Schwefel’s function

are similar. The population size and number of gen-

erations were the most important parameters. The

effects of the allocation of evaluations within and

between phases (including our new ﬁnal champion

phase) is roughly equivalent to the effect of varying

the population size or number of generations by a fac-

tor of two.

Finally, we were able to ﬁnd a strategy for soli-

taire Can’t Stop that performs better than the best pre-

viously known, which had been found using unopti-

mized GA parameters. The success was matched for a

parameterized non-optimal solitaire Yahtzee strategy.

OPTIMIZING GENETIC ALGORITHM PARAMETERS FOR A STOCHASTIC GAME

205

ACKNOWLEDGEMENTS

James Glenn was supported by sabbatical leave

granted by the Loyola College of Arts and Sciences

at Loyola University Maryland.

REFERENCES

Aizawa, A. and Wah, B. (1993). Scheduling of genetic al-

gorithms in a noisy environment. In Forrest, S., editor,

Proc. 5th Intl. Conf. on Genetic Algorithms, pages 48–

55, San Mateo, CA. Morgan Kaufman.

Arnold, D. and Beyer, H.-G. (2003). A comparison of evo-

lution strategies with other direct search methods in

the presense of noise. Comp. Opt. and App., 24:135–

159.

Bellman, R. E. (1957). Dynamic Programming. Princeton

University Press, Princeton, NJ, USA.

De Jong, K. (1975). An Analysis of the Behavior of a Class

of Genetic Adaptive Systems. PhD thesis, University

of Michigan.

Fang, H. (2005a). The nature of retrograde analysis for Chi-

nese chess, part I. ICGA Journal, 28(2):91–105.

Fang, H. (2005b). The nature of retrograde analysis for Chi-

nese chess, part II. ICGA Journal, 28(3):140–152.

Fitzpatrick, J. and Grefenstette, J. (1988). Genetic algo-

rithms in noisy environments. Machine Learning,

3:101–120.

Gasser, R. (1996). Solving nine men’s Morris. Computa-

tional Intelligence, 12:24–41.

Glenn, J. (2006). An optimal strategy for Yahtzee. Techni-

cal Report CS-TR-0002, Loyola College in Maryland,

4501 N. Charles St, Baltimore MD 21210, USA.

Glenn, J. (2007). Computer strategies for solitaire Yahtzee.

In IEEE Symp. on Comp. Intell. and Games, pages

132–139.

Glenn, J. and Aloi, C. (2009). A generalized heiristic for

can’t stop. In Proc. 22nd FLAIRS Conf., pages 421–

426. AAAI Press.

Glenn, J., Fang, H., and Kruskal, C. P. (2008). Retrograde

approximate algorithms for some stochastic games.

ICGA Journal, 31(2):77–96.

Irving, G., Donkers, J., and Uiterwijk, J. (2000). Solving

Kalah. ICGA Journal, 23(3):139–147.

Jin, Y. and Branke, J. (2005). Evolutionary optimization

in uncertain environments – a survey. Evolutionary

Computation, IEEE Transactions on, 9(3):303–317.

Keller, M. (1986). Can’t stop? Try the rule

of 28. World Game Review, 6. See also

http://www.solitairelaboratory.com/cantstop.html last

visited Nov. 22, 2008.

Lake, R., Schaeffer, J., and Lu, P. (1994). Solving large ret-

rograde analysis problems using a network of work-

stations. In van den Herik, H., Herschberg, I. S., and

Uiterwijk, J., editors, Advances in Computer Games

VII, pages 135–162. University of Limburg, Maas-

tricht. the Netherlands.

M¨uhlenbein, H. and Schlierkamp-Voosen, D. (1993). Pre-

dictive models for the breeder genetic algorithm. Evo-

lutionary Computation, 1:25–49.

M¨uhlenbein, H., Schornisch, M., and Born, J. (1991). The

parallel genetic algorithm as function optimizer. Par-

allel Computing, 17:619–632.

Neller, T. and Presser, C. (2004). Optimal play of the dice

game Pig. The UMAP Journal, 25(1):25–47.

Neller, T. and Presser, C. (2006). Pigtail: A Pig addendum.

The UMAP Journal, 26(4):443–458.

Romein, J. W. and Bal, H. E. (2003). Solving the game of

Awari using parallel retrograde analysis. IEEE Com-

puter Society, 36(10):26–33.

Sackson, S. (2007). Can’t Stop. Face 2 Face Games, Provi-

dence, RI, USA. Boxed game set.

Schaeffer, J., Bj¨ornsson, Y., Burch, N., Lake, R., Lu, P., and

Sutphen, S. (2004). Building the checkers 10-piece

endgame databases. In van den Herik, H., Iida, H.,

and Heinz, E., editors, Advances in Computer Games

10. Many Games, Many Challenges, pages 193–210.

Kluwer Academic Publishers, Boston, USA.

Str¨ohlein, T. (1970). Untersuchungen ¨uber kombinatorische

Spiele. PhD thesis, Fakult¨at f¨ur Allegemeine Wis-

senschaften der Technischen Hochschule M¨unchen,

Munich.

Thompson, K. (1986). Retrograde analysis of certain

endgames. ICCA Journal, 9(3):131–139.

Thompson, K. (1996). 6-piece endgames. ICCA Journal,

19(4):215–226.

T¨orn, A. and Zilinskas, A. (1989). Global Optimization.

Springer Verlag, New York.

Woodward, P. (2003). Yahtzee: The solution. Chance,

16(1):18–22.

Wu, R. and Beal, D. (2001). Fast, memory-efﬁcient retro-

grade algorithms. ICGA Journal, 24(3):147–159.

ICEC 2010 - International Conference on Evolutionary Computation

206