DISCOVERING CORTICAL ALGORITHMS
Atif G. Hashmi and Mikko H. Lipasti
Department of Electrical and Computer Engineering, University of Wisconsin - Madison
1415 Engineering Drive, Madison, WI - 53706, U.S.A.
Keywords:
Cortical columns, Unsupervised learning, Invariant representation, Supervised feedback, Inherent fault toler-
ance.
Abstract:
We describe a cortical architecture inspired by the structural and functional properties of the cortical columns
distributed and hierarchically organized throughout the mammalian neocortex. This results in a model which
is both computationally efficient and biologically plausible. The strength and robustness of our cortical ar-
chitecture is ascribed to its distributed and uniformly structured processing units and their local update rules.
Since our architecture avoids complexities involved in modeling individual neurons and their synaptic con-
nections, we can study other interesting neocortical properties like independent feature detection, feedback,
plasticity, invariant representation, etc. with ease. Using feedback, plasticity, object permanence, and temporal
associations, our architecture creates invariant representations for various similar patterns occurring within its
receptive field. We trained and tested our cortical architecture using a subset of handwritten digit images ob-
tained from the MNIST database. Our initial results show that our architecture uses unsupervised feedforward
processing as well as supervised feedback processing to differentiate handwritten digits from one another and
at the same time pools variations of the same digit together to generate invariant representations.
1 INTRODUCTION
Understanding of the structural and operational as-
pects of various components of the mammalian neo-
cortex has significantly increased over the past few
decades (Nicholls et al., 2001; Binzegger et al., 2004;
Ringach, 2004; Weng et al., 2006; Kalisman N, 2005;
Roth and Dicke, 2005; Hawkins and Blakeslee, 2005;
Sillito et al., 2006; Hirsch and Martinez, 2006; Ai-
mone et al., 2009). This has led to the develop-
ment of both low level biologically realistic as well as
high level biologically inspired computational mod-
els. Low level biologically realistic models include
the blue brain project (Markram, 2006), DARPA’s
SyNAPSE project (DARPA, 2008), and other simi-
lar projects. These models use neurons as their ba-
sic implementation abstraction and simulate detailed
low-level behavior of these neurons. Most of these
models use Hebbian rules (Clopath et al., 2007; Mar-
tinetz, 1993) along with detailed Spike Timing De-
pendent Plasticity (STDP) (Arthur and Boahen, 2006)
for learning and information processing. As a conse-
quence these models are intrinsically quite complex
and computationally very expensive. To cope with
these issues, other researchers have proposed biologi-
cally inspired high level learning models. These mod-
els implement some of the aspects of the neocor-
tex like uniform structure, hierarchy, spatial pooling,
temporal pooling, etc. Some of these models in-
clude ART (Carpenter et al., 1991), HTM (Hawkins
and George, 2006), Bayesian networks (George and
Hawkins., 2005), and deep belief networks (Hinton
et al., 2006). Even though these models are compu-
tationally quite efficient and implement some behav-
ioral aspects of the neocortex, they are quite divorced
from the actual biological structure and properties of
the neocortex. As a result, these models fail to match
the power and robustness of the mammalian neocor-
tex.
In this paper, we describe a cortical architecture
that models cortical columns found in the mammalian
neocortex (Mountcastle, 1978; Mountcastle, 1997) as
its basic structural and functional abstraction. Since
we model the structural and functional properties of
cortical columns, our architecture is computationally
quite efficient and biologically plausible as well. Our
model uses unsupervised feedforward processing and
plasticity principles to learn and extract independent
features from the patterns appearing within its recep-
tive field and it uses supervised feedback processing,
196
G. Hashmi A. and H. Lipasti M..
DISCOVERING CORTICAL ALGORITHMS.
DOI: 10.5220/0003079301960204
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
196-204
ISBN: 978-989-8425-32-4
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

object permanence, and temporal associativity to de-
velop invariant representations for variations of the
same pattern. To test and validate our cortical ar-
chitecture, we used a subset of handwritten digit im-
ages obtained from the MNIST database (Lecun and
Cortes, 1998). Our results show that our cortical ar-
chitecture learns to identify each of the unique digits
present in the sample set and it also pools variations
of the same digit together to develop invariant repre-
sentations.
The main contributions of this paper are as fol-
lows:
• We propose a cortical architecture that uses corti-
cal columns as its basic structural and functional
abstraction.
• We present detail modeling of feedforward and
lateral information processing algorithms that
columns used to identify independent features
from the patterns occurring in their receptive
fields.
• We hypothesizeand model how feedback process-
ing and temporal associations can be hierarchi-
cally utilized by the columns to learn invariant
representations for similar patterns.
• We hypothesize and model how the neocortex
might use feedback for better resource manage-
ment.
• Since in our model there is no separate training
and testing phase, it continues to evolve and learn
all the time.
• Due to its unsupervised learning rules, our model
contains an inherent resilience to permanent er-
rors (both in terms of hardware and software).
2 CORTICAL STRUCTURES AND
ORGANIZATION
The human brain can be divided into two main parts:
the old brain and the new brain. The old brain mainly
constitutes those parts of brain that developed early
in evolution. They include pathways from sensory
modalities to the new brain, spinal cord, and other
parts that deal with instinctual behavior. The new
brain, also referred to as the neocortex, is part of the
brain which is unique to mammals and is highly de-
veloped for humans; it accounts for about 77% of the
human brain (in volume) (Swanson, 1995). The neo-
cortex is responsible for perception, language, imag-
ination, mathematics, arts, music, planning, and all
the other aspects necessary for an intelligent system.
It contains virtually all our memories, knowledge,
skills, and experiences.
A very intriguing property of the neocortex
is its apparent structural and functional unifor-
mity (Mountcastle, 1978; Mountcastle, 1997). Be-
cause of this property, the regions of the neocor-
tex that process auditory inputs, for instance, ap-
pear very similar to the regions that handle visual
and other inputs. This uniformity suggests that even
though different regions specialize in different tasks,
they employ the same underlying algorithm. In
essence, the neocortex is a hierarchy of millions of
seemingly-identical functional units that are called
cortical columns. The concept of cortical columns
was introduced by Mountcastle in his seminal paper
in 1978 (Mountcastle, 1978). Since then, this concept
has been widely accepted and studied. Later studies
showed that cortical columns could further be classi-
fied into minicolumns and hypercolumns (Hubel and
Wiesel, 1962; Calvin, 1998; Johansson and Lansner,
2004; Ringach, 2004; Hirsch and Martinez, 2006). A
hypercolumn contains about 50 to 100 minicolumns,
and each of these minicolumns consists of around 200
to 300 neurons. The term cortical column is some-
times used for both types of columns, though, in lit-
erature, it usually refers to hypercolumns. The mini-
columns within the same hypercolumnshare the same
receptive field and are strongly connected with each
other through inhibitory lateral connections. Studies
(Hubel and Wiesel, 1962; Hubel and Wiesel, 1968)
hypothesize that the minicolumns use these paths to
learn unique/independent features from set of inputs
they are exposed to. The hypercolumns are then ar-
ranged in the form of a hierarchy throughout the neo-
cortex. Information flows up this hierarchy via excita-
tory feedforward paths and flows down the hierarchy
through feedback paths. Figure 1 shows the typical
structure of a hypercolumn.
The arrangement and functionality of the hyper-
columns and minicolumns has been studied in detail
in the visual cortex – the part of the neocortex respon-
sible for processing vision (Hubel and Wiesel, 1962;
Hubel and Wiesel, 1968; Binzegger et al., 2004; Sil-
lito et al., 2006; Peissig and Tarr, 2007). These stud-
ies suggest that minicolumns at the lower levels in
the hierarchy learn to identify very basic features like
edges of different orientation and communicate their
response to minicolumns at the upper levels. It is be-
lieved that cortical regions operate by progressively
abstracting and manipulating increasingly complex
notions throughout the neural hierarchy (Peissig and
Tarr, 2007). For instance, from the set of pixels of an
image, the visual cortex will first identify segments,
then elementary shapes such as angles and intersec-
tions, and increasingly complex combinations, such
DISCOVERING CORTICAL ALGORITHMS
197

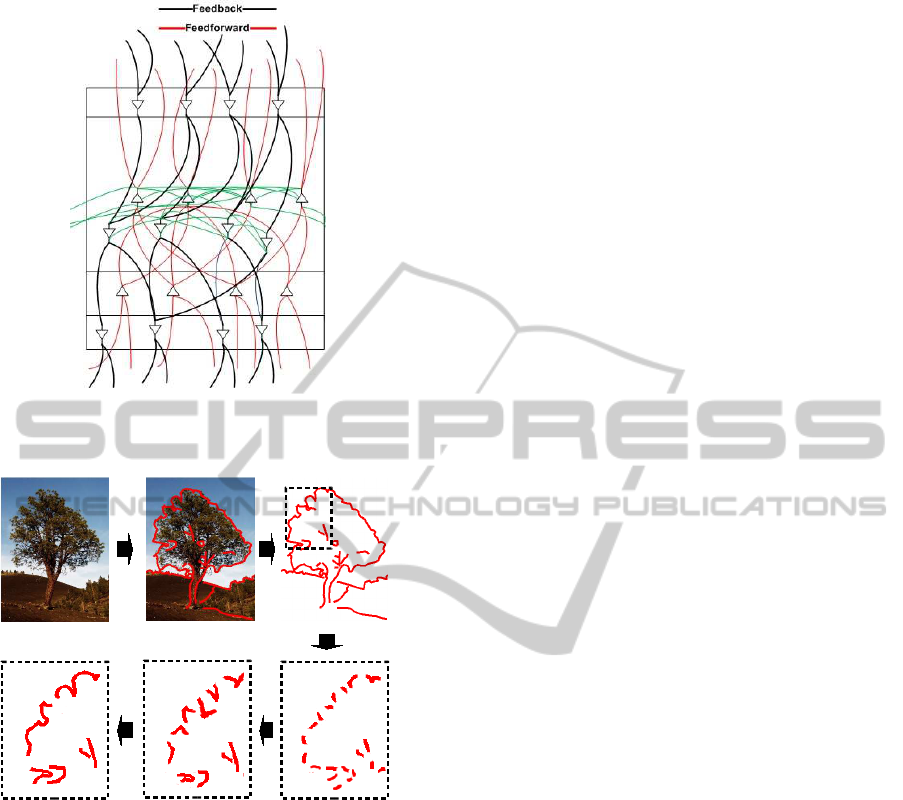
Figure 1: Forward, feedback and lateral connections be-
tween neurons and cortical columns.
Figure 2: Increasingly complex visual abstractions (seg-
ments, angles and long segments, complex shapes,...).
as objects found in our environment (Grill-Spector
et al., 1998), see Figure 2. This automatic abstrac-
tion capability for various inputs (visual, auditory, ol-
factory) partly explains why the neocortex still out-
performs traditional computers for a number of tasks,
such as face recognition, language learning, and mo-
tor control. Emulating such capability is thus a major
step in building computing systems that can compete
with the processing characteristics of the brain.
3 CORTICAL ARCHITECTURE
DESCRIPTION
3.1 Abstract Hypercolumn Model
As mentioned in Section 1, we model cortical
columns as our basic structural and functional imple-
mentation abstraction. Figure 3 shows the architec-
ture of the basic functional unit in our cortical model.
A hypercolumn consists of multiple minicolumns that
are strongly connected with each other via horizontal
inhibitory connections. All of the minicolumns within
a hypercolumn share the same receptive field. A re-
ceptive field is defined as the region within sensory
input that is associated to a hypercolumn.
3.2 Unsupervised Feedforward
Processing and Independent
Feature Learning
In our model each of the minicolumns within a hyper-
column learns to identify independent features from
the patterns appearing within its receptive field using
lateral inhibitory paths. This is quite in accordance
with the biological discussion presented in Section 2.
In this section, we provide detailed discussion on how
each of the minicolumns learns to identify these pat-
terns without any supervision.
3.2.1 Random Activations and Initial Learning
Initially all the minicolumns within a hypercolumn
are initialized with random weights. Thus, they show
no preference for any pattern that might occur within
their receptive field. Since our minicolumns also
model the stochastic nature of neurons by including
random neocortical firing behavior (Freeman, 1996;
Rokni et al., 2007), they exhibit high activations over
random intervals. When the random activation of a
specific minicolumn coincides frequently with vari-
ous occurrences of the same pattern, the minicolumn
adjusts its weights so that the correlation between the
weights and the input patterns increases. Thus over
time, that minicolumn develops a firing preference
for that specific pattern. While this random activa-
tion of minicolumns may not initially seem produc-
tive, this behavior is harnessed to make the model
fault-tolerant, improvesthe model’s training time, and
mimics the behavior of its biological inspirations.
3.2.2 Evaluating Output of Minicolumns
Each of the minicolumns contains a set of weights W
initialized to random values which are close to zero.
ICFC 2010 - International Conference on Fuzzy Computation
198

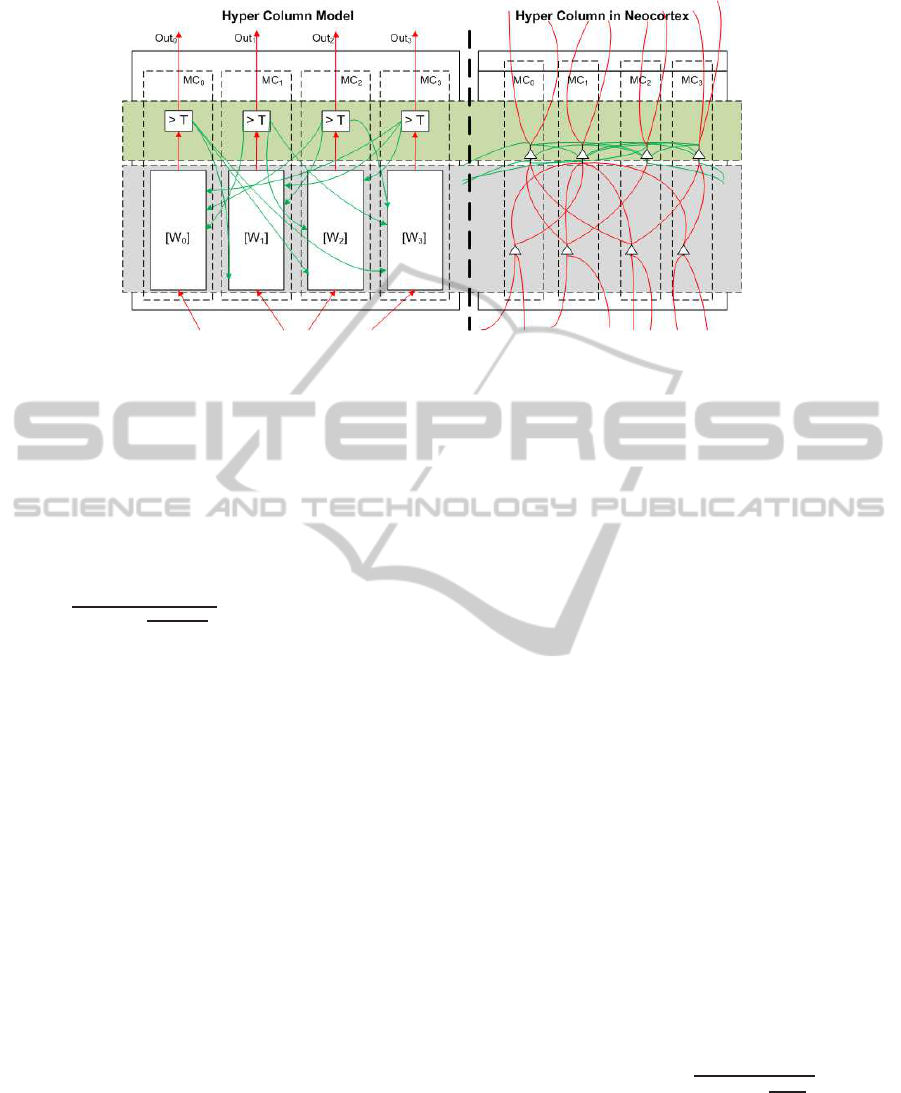
Figure 3: Mapping between our hypercolumn network and feedforward circuitry of a hypercolumn in the neocortex. The left
portion of the figure shows a Hypercolumn network with four minicolumns while the right portion shows the structure of a
typical hypercolumn. MC=Minicolumn, T=Threshold of Activation Function. A minicolumn fires if the dot-product of its
weights with the input is greater than the threshold.
During each training epoch, each of the minicolumns
evaluates the dot-product DP =
∑
N
i=1
X
i
.W
i
between
its weights
~
W and the input
~
X. The result of the dot-
product becomes the input to the activation function
given by,
1.0
1.0+ e
(−
DP−cuto f f
β
)
+ α ×
∑
|W
i
| (1)
Here, cutof f = φ×
∑
|W
i
|. φ determines the error tol-
erance of the minicolumn. β defines the sharpness of
the activation function while α controls the effect of
weight strength of a minicolumn on its output. The
minicolumn is said to fire if the value of its activation
function is greater than a determined threshold.
3.2.3 Lateral Inhibition and Independent
Feature Identification
Initially when an input
~
X is presented to the hyper-
column, none of the untrained minicolumns fire for
that input. However, if the random firing activity of a
minicolumn coincides with the occurrence of an in-
put pattern, that minicolumn adjusts its weights so
that the dot-productbetween the input and the weights
is improved. This is achieved by strengthening the
weights corresponding to the inputs X
i
that are cur-
rently active. Thus, over multiple iterations a mini-
column learns to identify a feature that initially co-
incided with the random activity of the minicolumn.
At the same time, each minicolumn inhibits neigh-
boring minicolumns from firing for the pattern it has
learned to recognize via lateral inhibitory connec-
tions. If multiple minicolumns fire at the same time,
the one with the strongest response inhibits the ones
with weaker responses. The inhibited minicolumns
then weaken their weights correspondingto highly ac-
tive X
i
so that their dot-product with the input is min-
imized. As a result of this process, the hypercolumn
network is able to recognize unique patterns without
any supervision. A very interesting byproduct of hav-
ing minicolumns learn independent features through
lateral inhibition is inherent fault tolerance. Lets as-
sume that a minicolumn that was firing for a feature
suddenly dies (permanent hardware or software error
in a future synthetic application) and stops firing for
that feature. It will not inhibit any other minicolumn
if that minicolumn fires for the same feature. Thus,
over time, another minicolumn with start firing for the
feature that was being recognized by the minicolumn
that just died. This makes our hypercolumn structure
inherently tolerant to permanent faults.
3.2.4 Weight Update Rules
Each time a minicolumn fires it modifies its weights
so that its correlation with the input pattern that has
caused it to fire increases. A minicolumn does that by
strengthening all the weights that correspond to the
input that are active at that time. To strengthen the
weights, we use the following update rule.
W
i
= X
i
× W
i
+ C
1
+ γ ×
1.0
1.0+ e
(−
W
i
−C
2
β
)
!!
(2)
Here, X
i
is the input corresponding to W
i
, C
1
de-
fines the minimum amount of update added to the cur-
rent W
i
and C
2
defines how the present W
i
will affect
the weight update. In our weight strengthening rule,
the update added to W
i
is dependent upon the present
value of W
i
as well. This means that if W
i
is strong it
DISCOVERING CORTICAL ALGORITHMS
199

will get a higher update value. This is quite in accor-
dance with biological data (Rokni et al., 2007; Seung,
2003).
In the case when a minicolumn is inhibited, it
modifies the weights using the following update rule.
W
i
= X
i
× (W
i
− δ) (3)
Here, δ defines the weight update rate in the pres-
ence of inhibition. It should be noted that other com-
plex update can also be used here.
Apart from updating the weights in the presence of
excitation and inhibition, the weights also decay over
time. This is quite similar to the forgetting behavior in
animals. This update is done using a rule quite similar
to the one used for excitatory updates and is given by.
W
i
= W
i
+ C
3
+ ε × 1−
1.0
1.0+ e
(−
W
i
−C
2
β
)
!!
(4)
Here, C
3
is the minimum amount of decay while ε
increase in forgetting rate proportional to the current
weight value. It should be noted that C
3
<< C
1
and
ε << γ. This insures that the forgetting rate is signif-
icantly smaller than the learning rate. This is quite in
accordance with the existing biological data.
3.3 Hierarchical Arrangement of
Hypercolumns
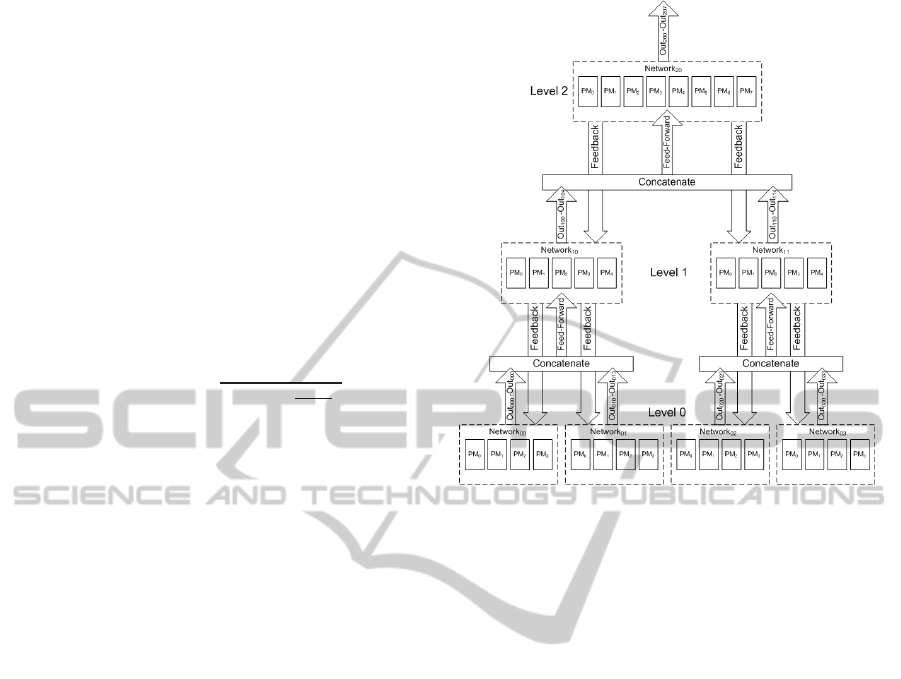
To perform complex tasks the hypercolumns can be
arranged in the form of a hierarchy. Lower hierar-
chical levels identify simple features and communi-
cate their output to the higher levels via feedforward
paths. Each of the higher level hypercolumnsreceives
inputs from multiple lower level hypercolumns. In
this manner the activations flow up the hierarchy and
the minicolumns in the top-level hypercolumns train
themselves to identify each of the complex unique
pattern from the input. Each level of this hierarchy
behaves the same way as different levels of the vi-
sual cortex i.e. in the case of image recognition,
lower level hypercolumns detect edges, and the hy-
percolumns at the higher levels detect progressively
complex features. A simple hierarchical arrangement
of multiple hypercolumns with feedforward and feed-
back paths is shown in Figure 4. It should be noted
that our hierarchical model supports any complex hi-
erarchical arrangement of hypercolumns.
3.4 Supervised Feedback Processing
and Invariant Representations
Our feedforward learning process enables our corti-
cal hierarchy to learn unique features from the input
Figure 4: A simple hierarchical arrangement of multiple hy-
percolumns.
patterns. Even though each of the minicolumns can
withstand and fire for patterns with small variations
but patterns with significant variations are recognized
as different features. This means that two variations
of the same pattern might be recognized as two differ-
ent features. To resolve this issue and generate invari-
ant representation for variations of the same pattern,
we make use of our supervised feedback processing
algorithm.
Lets assume that our hierarchical network has
started to recognize a pattern. Now it is exposed to an-
other variation of the same patterns that is quite differ-
ent from the previous one e.g. two different variations
of a handwritten digit. At this point, only some of the
minicolumns within the hierarchy might now fire. As
a result, the top level minicolumn that is supposed to
fire for that pattern does not fire. If this behavior per-
sists, new minicolumns will train themselves to rec-
ognize features in the new variation that are quite dif-
ferent from the original pattern. Over time, that new
variation will be identified as a new pattern. This will
be marked by firing of a minicolumn in the top level
of the hierarchy. At this point, the top level hypercol-
umn receives a feedback signal. This feedback signal
forces the minicolumn firing for the original pattern
to fire and also inhibits the minicolumn that is firing
for the new variation. Now, the minicolumn receiving
excitatory feedback also adjusts its weights so that it
fires for the new variation as well while the inhibited
ICFC 2010 - International Conference on Fuzzy Computation
200

minicolumn changes its weights so that it does
not fire for that input pattern. Thus over multiple
exposures, the minicolumn firing for the original
pattern will also start to fire for the new variation.
Once the top level minicolumn starts to give a stable
activation for both the variations, it will start to
send the feedback signal down so that lower level
minicolumns can also create invariant representa-
tions. The amount of feedback sent to each of the
lower level minicolumns is proportional to its firing
history i.e. if a minicolumn has been firing a lot
in the past, it will get stronger feedback. Thus,
over time most active minicolumn ends up pooling
its child minicolumns to generate invariant repre-
sentations and inhibits its neighbours from firing.
This results in significant resource optimization.
The process of generating invariant representations
within a minicolumn using feedback is explained
in the pseudo-code provided in Algorithm 1.
In Algorithm 1, UpdateSynapticWtsExcitatory
models the functionality of Equation 2 while
U pdateSynapticWtsInhibitory models Equation 3.
Algorithm 1: Pseudo code for generating invariant
representations within a minicolumn using supervised
feedback.
if feedback > 0 then
if hasNotFired then
if hasMaxFiringHistory then
U pdateSynapticWtsExcitatory( feedback)
end if
else
if hasMaxFiringHistory then
U pdateSynapticWtsExcitatory( feedback)
if isStable then
for i = 1 to N do
if IsActive(child[i]) then
SendFBToChild(i, feedback)
end if
end for
end if
else
U pdateSynapticWtsInhibitory( feedback)
end if
end if
end if
4 EXPERIMENTS AND RESULTS
To test and validate different properties of our corti-
cal architecture and to evaluate its learning and recog-
nition performance, we used a subset of handwritten
digit images obtained from the MNIST database (Le-
cun and Cortes, 1998). For this digit recognition task,
we created a hierarchical network with 6 levels. We
initialized this network as described in Table 1. Level
0 corresponds to the lowest level in the hierarchy. All
the digits in the MNIST database are in the form of
28x28 pixel wide black and white images. Out of the
28 rows, top 2 and bottom 2 rows were always black.
Thus, in our experiments, we ignored these rows to
save on execution time. Each of the remaining rows
becomes the input to one of the twenty four Level 0
hypercolumns.
Table 1: Detailed description of the hierarchical network
created for recognition of handwritten digit images.
Level Hypercolumns (HC) Minicolumns/HC
5 1 100
4 1 200
3 3 200
2 6 200
1 12 300
0 24 500
4.1 Experiment 1: Feedforward
Processing and Independent
Feature Recognition
In the first experiment, we validated our feedforward
information processing and learning algorithm. For
this experiment, we disabled the feedback process-
ing and studied how the network learns independent
features from the input patterns. Since there was
no feedback, we anticipate that in Level 5 (top most
level) of the hierarchy, variations of same digits will
be recognized by different minicolumns. For this ex-
periment, we took 100 handwritten digit images (10
variations of each digit) from the MNIST database
and trained and tested our network with them till it
achieved 100% recognition rate. Figure 5 shows the
results of this experiment.
In Figure 5, we can see that the top level hyper-
column contains 89 minicolumns that have learned to
recognize various digit patterns present in the input
dataset. 11 digit variations are pooled with some other
variation of the same digit due to spatial similarities.
4.2 Experiment 2: Feedback Processing
and Invariant Representation
To test how our feedback processing algorithm gen-
erates invariant representations, we used the same hi-
erarchical network mentioned above. For the input
DISCOVERING CORTICAL ALGORITHMS
201

0
10
20
30
40
50
60
70
80
90
0 10 20 30 40 50 60 70 80 90 100
Number of Unique Digits Recognized
Number of Digits in Input Dataset
Figure 5: Unique digit variations learned by the hierarchical
network in the absence of feedback.
dataset, we used the same 100 digit images (10 vari-
ations for each digit) for training as used in Exper-
iment 1 and trained the network with these images
till the network achieved 100% recognition rate. At
this point, we noticed that there were only 10 mini-
columns in the top level hypercolumn that were firing
in response to the digits being exposed to the network.
This meant that there was just one minicolumn fir-
ing for all the different variations of the same digit.
We also evaluated the resource optimization achieved
through feedback processing. To do that we calcu-
lated the number of active minicolumns in the hierar-
chical network with and without feedback. In steady
state, without feedback the network used 3876 mini-
columns while with feedback it only used 1283 mini-
columns. Thus, our feedback processing algorithm
results in about 3x resource optimization.
4.3 Experiment 3: Robustness to Test
Images
In this experiment, we tested the robustness of our
cortical network to the patterns not present in the
training dataset. For this experiment we again used
the same hierarchical network described above. We
used 400 handwritten digits images (40 variations of
each digit) training images and 40 test images (4 vari-
ations of each digit). We then trained the network
with the images till the images in the training dataset
till the network achieved 100% recognition rate and
was in a stable state i.e. all the levels in the hierar-
chy had generated invariant representations for all the
input digit variations. Figure 6 shows the recognition
rate of the network as the number of images in the
training dataset is increased from 10 to 400. For this
experiment, recognition rate is defined as the percent-
age of the images in the test dataset that were recog-
nized correctly.
After training with 400 images, our hierarchical
network achieves a recognition rate of around 80%
0
10
20
30
40
50
60
70
80
10 40
70
100
130 160
190
220 250 280 310
340 370
400
Recognition Rate (%)
Number of Training Handwritten Images
Figure 6: Recognition rate of the network for handwritten
test digit images as the number of training images is in-
creased.
for the 40 test images. We believe that as we increase
the number of training images the recognition rate can
further be increased. Presently, we cannot create re-
ally big networks due to memory and training time
limitations. In the future we are planning to extend
our cortical architecture so that it can run on NVidia
GPUs. This will let us create and test large hypercol-
umn based networks and will overcome this issue.
4.4 Experiment 4: Inherent Fault
Tolerance
The final experiment that we conducted studies and
validates the inherent fault-tolerant property of our
cortical network. For this experiment, we used the
same hierarchy as described above and used 200
handwritten digit images for training. To reduce the
execution time for each epoch, we limited the feed-
back processing to Level 5 (top-most level) of the hi-
erarchy only. Initially, we trained the hierarchy with
all the 200 images till it achieved 100% recognition
rate. At this point we corrupted 5% of the total num-
ber of minicolumns throughout the hierarchy. This
was done by randomly selecting minicolumns and
forcing their output to stay 0 permanently. Then we
evaluated the recognition rate of the hierarchy with
all the 200 training images to determine the amount
of loss in recognition. Then we trained the damaged
hierarchy with the same training images and evalu-
ated the peak recognition rate for the training images.
We repeated this cycle multiple times corrupting 5%
of the original number of minicolumns every time to
observe how the hierarhcy behaves as we inject more
and more permanent faults. Table 2 shows the behav-
ior of our cortical network in the presence of perma-
nent faults.
When Fault Injection Attempt is 5 that means that
we have damaged 25% of the total minicolumns orig-
inally present in the hierarchy. For this attempt, after
ICFC 2010 - International Conference on Fuzzy Computation
202

Table 2: Evaluation of the inherent fault tolerance prop-
erty of our cortical network. Initial Recognition Rate means
the recognition rate (percentage) measured immediately af-
ter the faults are injected. Peak Recognition Rate means
the maximum recognition rate achieved through training the
damaged network.
Fault Injec-
tion Attempt
Initial Recog-
nition Rate
(%age)
Peak Recog-
nition Rate
(%age)
1 92 100
2 89 100
3 90 100
4 88 100
5 88 94
6 82 82
7 71 71
8 65 65
training the damaged hierarchy, it achieves the peak
recognition rate of 94%. This is due to the fact that
some of the hypercolumns ran out of the minicolumns
that were idle. As a result the features being recog-
nized by the minicolumns that were damaged could
not be relearned. This experiment also shows that as
long as there are idle resources available in the net-
work, it can recover from permanent faults.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we havedescribed a hierarchical cortical
architecture that uses the concept of cortical columns
as its basic structural and functional abstraction. We
have demonstrated that building models based on the
properties of cortical columns can be computation-
ally efficient as well as biologically plausible. Using
these models, we can study various neocortical prop-
erties like independent feature identification, feed-
back, plasticity, invariant representation, and resource
management.
In the future, we plan to validate our hypercolumn
unit using STDP level models. We also plan to ex-
tend our model so that it can run on NVidia GPUs
so that we can create huge hypercolumn networks for
real world applications. We also plan to add other in-
teresting neocortical features like temporal sequence
learning, memory, attention, etc. in our model.
REFERENCES
Aimone, J., Wiles, J., and Gage, F. (2009). Computational
influence of adult neurogenesis on memory encoding.
Neuron, 61(2):187–2002.
Arthur, J. and Boahen, K. (2006). Learning in silicon: Tim-
ing is everything. In Proceedings of Advances in Neu-
ral Information Processing Systems, volume 18, pages
75–82. Advances in Neural Information Processing
Systems.
Binzegger, T., Douglas, R., and Martin, K. (2004). A quan-
titative map of the circuit of cat primary visual cortex.
J. Neurosci., 24(39):8441–8453.
Calvin, W. (1998). Cortical columns, modules, and hebbian
cell assemblies. In Arbib, M. A., editor, The Hand-
book of Brain Theory and Neural Networks, pages
269–272. MIT Press, Cambridge, MA.
Carpenter, G., Grossberg, S., and Rosen, D. (1991). Art2-
a: An adaptive resonance algorithm for rapid category
learning and recognition. Neural Networks, 4:493–
504.
Clopath, C., Longtin, A., , and Gerstner, W. (2007). An
online hebbian learning rule that performs indepen-
dent component analysis. In Proceedings of Neural
Information Processing Systems. Neural Information
Processing Systems.
DARPA (2008). Systems of neuromorphic adap-
tive plastic scalable electronics (synapse).
http://www.darpa.mil/dso/thrusts/bio/biologically/
synapse/.
Freeman, W. (1996). Random activity at the microscopic
neural level in cortex (”noise”) sustains and is reg-
ulated by low-dimensional dynamics of macroscopic
activity (”chaos”). International Journal of Neural
Systems, 7(4):473–480.
George, D. and Hawkins., J. (2005). A hierarchical bayesian
model of invariant pattern recognition in the visual
cortex. In Proceedings of International Joint Con-
ference on Neural Networks, volume 3, pages 1812–
1817. IEEE International Joint Conference on Neural
Network.
Grill-Spector, K., Kushnir, T., Hendler, T., Edelman, S.,
Itzchak, Y., and Malach, R. (1998). A sequence of
object-processing stages revealed by fmri in the hu-
man occipital lobe. Hum. Brain Map., 6:316–328.
Hawkins, J. and Blakeslee, S. (2005). On Intelligence.
Henry Holt & Company, Inc.
Hawkins, J. and George, D. (2006). Hierarchical temporal
memory. www.numenta.com/Numenta HTM Conce
pts.pdf.
Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006). A fast
learning algorithm for deep belief nets. Neural Com-
put., 18(7):1527–1554.
Hirsch, J. and Martinez, L. (2006). Laminar processing in
the visual cortical column. Current Opinion in Neuro-
biology, 16:377–384.
Hubel, D. and Wiesel, T. (1962). Receptive fields, binocular
interactions and functional architecture in cat’s visual
cortex. Journal of Physiology, 160:106–154.
Hubel, D. and Wiesel, T. (1968). Receptive fields and func-
tional architecture of monkey striate cortex. Journal
of Physiology, 195:215–243.
DISCOVERING CORTICAL ALGORITHMS
203

Johansson, C. and Lansner, A. (2004). Towards cortex sized
artificial nervous systems. Lecture Notes in Com-
puter Science: Knowledge-Based Intelligent Informa-
tion and Engineering Systems, 3213:959–966.
Kalisman N, Silberberg G, M. H. (2005). The neocortical
microcircuit as a tabula rasa. Proc. Natl. Acad. Sci.
USA, 102, 880-885.
Lecun, Y. and Cortes, C. (1998). The mnist database of
handwritten digits. http://yann.lecun.com/exdb/
mnist/.
Markram, H. (2006). The blue brain project. In SC
’06: Proceedings of the 2006 ACM/IEEE conference
on Supercomputing, page 53, New York, NY, USA.
ACM.
Martinetz, T. (1993). Competitive hebbian learning rule
forms perfectly topology preserving maps. In Inter-
national Conference on Artificial Neural Networks,
ICANN, pages 427 –434.
Mountcastle, V. (1978). An organizing principle for cere-
bral function: The unit model and the distributed sys-
tem. In Edelman, G. and Mountcastle, V., editors, The
Mindful Brain. MIT Press, Cambridge, Mass.
Mountcastle, V. (1997). The columnar organization of the
neocortex. Brain, 120:701–722.
Nicholls, J., Martin, A., Wallace, B., and Fuchs, F. (2001).
From Neuron To Brain. Sinauer Associates Ins, 23
Plumtree Road, Sunderland, MA, USA.
Peissig, J. and Tarr, M. (2007). Visual object recognition:
do we know more now than we did 20 years ago?
Annu. Rev. Psychol., 58:75–96.
Ringach, D. (2004). Haphazard wiring of simple receptive
fields and orientation columns in visual cortex. J. Neu-
rophysiol., 92(1):468–476.
Rokni, U., Richardson, A., Bizzi, E., and Seung, H. (2007).
Motor learning with unstable neural representations.
Neuron, 64:653–666.
Roth, G. and Dicke, U. (2005). Evolution of brain and intel-
ligence. TRENDS in Cognitive Sciences, 5:250–257.
Seung, H. (2003). Learning in spiking neural networks
by reinforcement of stochastic synaptic transmission.
Neuron, 40:1063–1073.
Sillito, A., Cudeiro, J., and Jones, H.(2006). Always return-
ing: feedback and sensory processing in visual cortex
and thalamus. Trends Neurosci., 29(6):307–316.
Swanson, L. (1995). Mapping the human brain: past,
present, and future. Trends in Neurosciences,
18(11):471 –474.
Weng, C., Yeh, C., Stoelzel, C., and Alonso, J. (2006). Re-
ceptive field size and response latency are correlated
within the cat visual thalamus. Journal of Neurophys-
iology, 93:3537 –3547.
ICFC 2010 - International Conference on Fuzzy Computation
204