AN INVESTIGATION OF THE EFFECT OF

INPUT REPRESENTATION IN ANFIS MODELLING

OF BREAST CANCER SURVIVAL

Hazlina Hamdan and Jonathan M. Garibaldi

Intelligent Modelling and Analysis (IMA) Research Group, School of Computer Science

The University of Nottingham, Jubilee Campus, Wollaton Road, Nottingham, NG8 1BB, U.K.

Keywords:

Adaptive neuro-fuzzy inference system, Survival analysis, Breast cancer, Nottingham prognostic index.

Abstract:

Fuzzy inference systems have been applied in recent years in various medical ﬁelds due to their ability to

obtain good results featuring white-box models. Adaptive Neuro-Fuzzy Inference System (ANFIS), which

combines adaptive neural network capabilities with the fuzzy logic qualitative approach, has been previously

used in modelling survival of breast cancer patients based on patient groups derived from the Nottingham

Prognostic Index (NPI), as discussed in our previous paper. In this paper, we extend our previous work to

examine whether the ANFIS model can be trained to better match the data with the NPI variable represented

as a real number, rather than a categorical group. Two input models have been developed and trained with

different structures of ANFIS. The performance of these models, in the capability to predict the survival rate

in survival of patients following operative surgery for breast cancer, is examined.

1 INTRODUCTION

The use of artiﬁcial intelligence (AI) techniques in the

medical ﬁeld in the early 1970s emerged to model ex-

pert behaviour by utilising the knowledge and repre-

senting it in symbolic form. Medical AI has since

become very popular and has more recently been ac-

cepted by clinicians for its ability to produce high-

quality results and demonstrate improvements upon

previous techniques used (Joseph and David, 2006).

In clinical situations such as diagnosis, treatment and

prognosis in which there are complex interactions of

clinical, biological and pathological variables, com-

puterised analytical tools are needed to exploit the re-

lationships between these variables. Soft-computing

approaches including artiﬁcial neural networks and

fuzzy inference systems (and many others) have been

used to address this problem.

An artiﬁcial neural network (ANN) is an infor-

mation processing system inspired by the structure

of the human brain. ANNs have been the sub-

ject of great interest, following the discovery of the

back-propagation algorithm, and recently have be-

come very popular in the prediction of survival in

medical contexts (Joseph and David, 2006; Lisboa,

2002; Burke et al., 1997). With their ability to learn

through experience, neural networks work by detect-

ing patterns in data, learning from the relationships

and adapting to them. This knowledge is then used to

predict the outcome for new combinations of data.

Fuzzy inference is based on the concepts of fuzzy

set theory, fuzzy if-then rules, and fuzzy reasoning in

which a mapping from a given input to an output is

deﬁned based on expert knowledge. The knowledge

is encoded as a set of explicit linguistic rules, which

can be easily understood by people without techni-

cal expertise. In medical ﬁelds, fuzzy inference have

been used extensively for over a decade in data clas-

siﬁcation, decision analysis, diagnosis and prognosis

(Yardimci, 2009). As fuzzy information deals with

knowledge that is uncertain, ambiguous or imprecise,

it is suitable to be used in the medical contexts to rep-

resent certain elements as members of sets with some

degree of membership.

A hybrid methodology which combines the ad-

vantages of ANNs and fuzzy inference known as

adaptive neuro-fuzzy inference system (ANFIS) tech-

nique was presented in modelling survival (Hamdan

and Garibaldi, 2010). In this previous study, the Not-

tingham Prognostic Index (NPI) variable was repre-

sented as a categorical group. We now present a fur-

ther study in which we extend our previous work by

examining whether the ANFIS model can be trained

to better match the data with the NPI variable repre-

Hamdan H. and M. Garibaldi J..

AN INVESTIGATION OF THE EFFECT OF INPUT REPRESENTATION IN ANFIS MODELLING OF BREAST CANCER SURVIVAL.

DOI: 10.5220/0003081100990104

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICFC-2010), pages

99-104

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

sented as a real number. In addition, two input models

are presented to the ANFIS model and comparison of

these two models is made as to the effect of member-

ship function and generalization performance.

2 BACKGROUND

2.1 Breast Cancer

Cancer is a leading cause of death worldwide, as

reported by the World Health Organization (WHO,

2010). Lung, stomach, liver, colon and breast can-

cer are all major contributors to the overall cancer

mortality each year. Breast cancer is one of the most

common cancers to afﬂict the female population. It is

estimated that one in nine women in the UK will de-

velop breast cancer at some point in their life (Cancer

Research UK, 2010).

Breast cancer is a malignant tumour that devel-

ops from uncontrolled growth of cells in the breast.

A malignant tumour is composed of cells that invade

or spread to other parts of the body. The exact cause

of the breast cancer is not really known, but is most

likely to be a combination of genetic and environmen-

tal factors. However, in general, earlier diagnosis and

treatment should increase the survival rates, as the dis-

ease is much easier to control if it has not spread to

other parts of the body.

Breast cancer patients can be assigned into prog-

nosis groups using a ‘prognostic index’. The ‘Not-

tingham Prognostic Index’ (NPI) has been widely ac-

cepted in clinical practice to categorise patients into

high (78%), intermediate (50%) or low (20%) risk

groups. This index is based on pathological size,

grade of tumor and the number of axillary nodes ef-

fected are identiﬁed signiﬁcant in the prediction of

survival (Galea et al., 1992). The NPI score can be

calculated as:

NPI=0.2*pathological tumor size(cm)+lymph node

stage+histological grade

Table 1 shows the accepted clinical cut-offs of the

NPI score into categories patient into ‘good’, ‘moder-

ate’ or ‘poor’.

Table 1: Category of NPI score.

NPI score Category

Less than 3.41 Good

Between 3.41 to 5.4 Moderate

Over 5.4 Poor

2.2 Survival Analysis

Survival analysis describes the analysis of data that

corresponds to the time from when an individual en-

ters a study until the occurrence of some particular

event or end-point. In medical contexts, the event can

be the response to a treatment, recurrence or disease-

free survival, or death. An individuals with cancer

cannot all be observed for the same length of time,

because some individual are diagnosed at the begin-

ning of the period under study, some near the end and

others may be diagnosed at any time in the study.

Basically, survival data contains uncensored and

censored observations. Uncensored observations in-

volved patients who are observed until they reach the

end of the study. Censored observations on the other

hand, involve only patients who survive beyond the

end or who are lost to follow-up at some point.

The survival function is deﬁned as the probability

that an individual survives longer than time t, where T

denotes a positive random variable associated with the

survival time, represented as (Biganzoli et al., 1998):

S(t) = P(T > t) (1)

On the other hand, the hazard function, also known

as conditional failure probability, is the probability an

individual will die at a certain time t (conditioned on

survival up to that time) and so denotes the instanta-

neous death rate. It can be shown in this form:

= P(T ∈ A

|T > t

l−1

) =



S(t

l−1

) − S(t

)

S(t

l−1

)



(2)

where the time interval l = 1, 2, ..., L forms disjoint

intervals A

= (t

l−1

The survival and hazard functions are related to

each other, in that the estimation of survival function

can be written as:

S(t) =

∏

l:t

≤t

(1 − h

) (3)

Statistical methods, such as the Kaplan-Meier es-

timate, are usually used to explain the data and to

model the disease progression with the ability to han-

dle censored data. A plot of the Kaplan-Meier is to

represent the estimation of the survival function of

some particular groups against time, can be view as

a series of horizontal steps of declining magnitude.

2.3 ANFIS Architecture

The use of fuzzy logic in medical contexts may be

said have been introduced by (Zadeh, 1969) in his pa-

per entitled ‘Biological application of the theory of

ICFC 2010 - International Conference on Fuzzy Computation

100

fuzzy sets and system’ (Yardimci, 2009; ?). Fuzzy

logic is based on fuzzy sets that use linguistic vari-

ables with certain degree of membership and which

can then be connected using IF-THEN rules to form

a series of fuzzy rules. Fuzzy rules can have mul-

tiple antecedents connected with AND or OR opera-

tors, where all parts are calculated simultaneously and

resolved into a single number. Consequents can also

be comprised of multiple parts, which are then aggre-

gated into a single output of a fuzzy set (Negnevitsky,

2005).

Fuzzy inference is a process of mapping from a

given input to an output using the methods of fuzzy

set manipulations. Two types of fuzzy inference most

commonly used are the Mamdani method (Mamdani

and Assilian, 1975) and the Sugeno method (Sugeno,

1985). The difference between these two fuzzy infer-

ences methodologies is the speciﬁcation of the con-

sequent part. In the Mamdani method, consequents

are fuzzy sets, and the ﬁnal crisp output of Mam-

dani method is based on defuzziﬁcation of the over-

all fuzzy output using various types of defuzziﬁcation

method. In contrast, in the Sugeno method, conse-

quents are real numbers, which can be either linear or

constant (zero-order Sugeno model). The ﬁnal output

(known as a singleton output membership function),

is the weighted average of each rule’s output.

Using an adaptation of the Sugeno fuzzy inference

method, (Jang, 1993) proposed the adaptive neuro-

fuzzy inference system (ANFIS) method that com-

bined the neural network adaptive capabilities and

the fuzzy logic qualitative approach. The ANFIS

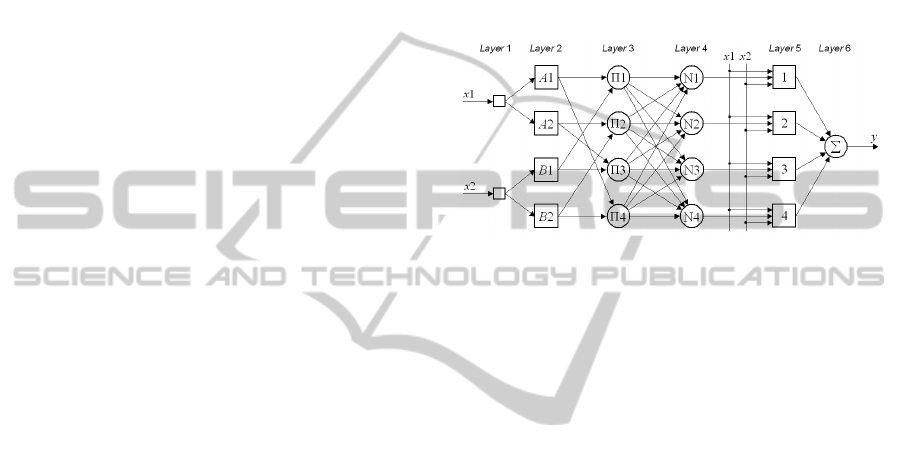
architecture contains a six-layer feed-forward neural

network as shown in Figure 1 (Negnevitsky, 2005).

Brieﬂy, the functional of each layer are as given be-

low:

Layer 1 is the input layer that passes external crisp

signals to Layer 2.

Layer 2 known as the fuzziﬁcation layer, to deter-

mine the membership grades for each input imple-

mented by the given fuzzy membership function.

Layer 3 is the rule layer, which calculates the ﬁring

strength of the rule as the product of the member-

ship grades.

Layer 4 called the ‘normalised ﬁring strengths’, in

which each neuron in the layer receives inputs

from all neurons in Layer 3, and calculates the ra-

tio of the ﬁring strength of a given rule to the sum

of ﬁring strengths of all rules.

Layer 5 is the defuzziﬁcation layer that yields the

parameters of the consequent part of the rule.

Layer 6 is a single node that calculates the overall

output as the summation of all incoming signals.

Full details of the ANFIS process can be found in

(Jang, 1993) and (Negnevitsky, 2005).

ANFIS training can use alternative algorithms to

reduce the error of the training. A hybrid approach,

featuring a combination of the gradient descent algo-

rithm and a least squares algorithm, is used for an ef-

fective search for the optimal parameters. The main

beneﬁt of such a hybrid approach is that it converges

much faster, since it reduces the search space dimen-

sions of the backpropagation method used in neural

networks (Jang, 1993).

Figure 1: Adaptive Neuro-Fuzzy Inference System (AN-

FIS).

3 DATA AND METHODS

3.1 Data

A set of 958 breast cancer patients collected by the

Breast Cancer Pathology Research Group in the Uni-

versity of Nottingham were used in a previous study

to model the survival curve using the ANFIS model

(Hamdan and Garibaldi, 2010). In the study, the pa-

tients are assigned into three groups of NPI whether

good, moderate or poor (represented as 1, 2, and 3,

respectively) based on the clinical cut-offs as shown

in Table 1.

In this study, we used the same data set as a pre-

vious study with two variables as the input which are

NPI values and survival time. However, the NPI vari-

able in this study is presented as a real number (orig-

inal values from the clinical). The ANFIS model was

applied to the data set to examine whether the mem-

bership functions of a real-valued NPI can be trained

to better match the data.

3.2 Methods

Data pre-processing was based on that of the non-

linear method known as Partial Logistic Artiﬁcial

Neural Network (PLANN) (Biganzoli et al., 1998)

to produce smooth estimation of hazard rate. This

method was created to allow the use of a standard

AN INVESTIGATION OF THE EFFECT OF INPUT REPRESENTATION IN ANFIS MODELLING OF BREAST

CANCER SURVIVAL

101

back-propagation ANN architecture to be used for

modelling survival. A major process is to perform

a speciﬁc form of data replication that was used in

training phase of ANFIS method.

As stated in a previous study (Hamdan and

Garibaldi, 2010), for training purposes, each patient

is replicated for all the intervals in which the patient

is observed, using the event indicator as the target.

The input of the network (survival time and NPI val-

ues) is replicated into t times which is the maximum

survival time of an individual patient. The event at-

tribute as a target of the network is also replicated and

assigned as zero until the last time value is reached,

where the event is 1 for occurrence and zero for cen-

sored. An example of replication as shown in Table 2

which suitable to be train by the ANFIS.

While for the testing data to ﬁnd the estimation

of hazard rate for each interval time, each patient is

replicated until the maximum time is observed or the

full study time is reached. The hazard rate for each

interval is the mean of hazard rate of all patient in that

particular interval, and this depends on the cut-off of

NPI to group the patients into good, moderate or poor.

The estimation of survival function is determined us-

ing equation (3).

Initial parameters of the fuzzy inference system

have to be established before the training process

commences. Several ANFIS model were conﬁgured

with different numbers of membership functions for

the survival time, ranging from 3 to 7 and the number

of membership functions for the NPI variable is based

on the clinical groups (which is three). Gaussians

were used for the membership functions and constants

were used for the rule outputs (a zeroth-order Sugeno

model). Hybrid learning, the combination of gradient

descent and least squares algorithm, was selected as

the learning algorithm.

4 EXPERIMENTAL RESULTS

AND DISCUSSION

Data from 958 breast cancer patients were subjected

to the pre-processing described above before being

passed to the training process. This section presents

the result of two models input into the ANFIS model:

the ﬁnal membership function generated, the learning

rate and the conditional event probability will be dis-

cussed. Also, a comparison of survival rate of two

input models is made according to the Kaplan-Meier

method.

Two models of inputs are presented to the AN-

FIS model. In the ﬁrst input model, the survival time

is based in months with an observation time of 120

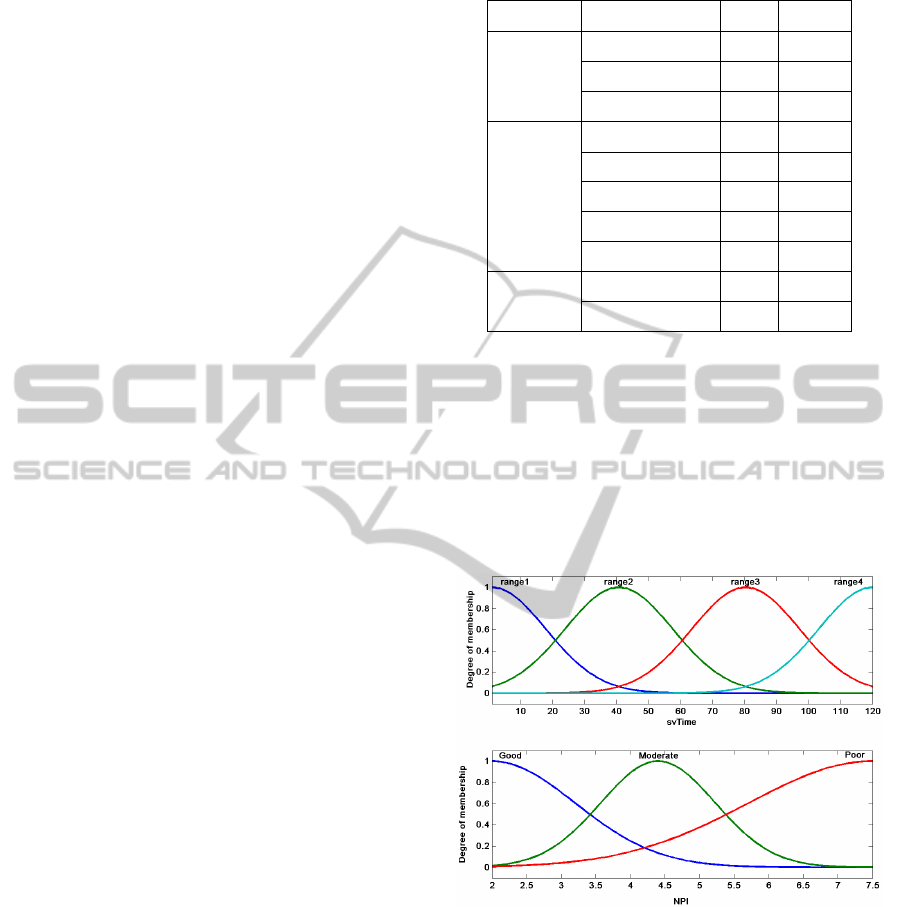
Table 2: Replication for training.

Time interval NPI Event

1 4.4 0

Patient 1 2 4.4 0

3 4.4 1

1 2.8 0

2 2.8 0

Patient 2 3 2.8 0

4 2.8 0

5 2.8 0

Patient 3 1 6.3 0

2 6.3 1

months while, in the second input model, the survival

time was transformed into a yearly basis, correspond-

ing to a ten year period of observation. Both models

used real values of NPI.

Four membership functions of survival time were

ﬁnally selected as it was observed that these provided

a smooth conditional hazard function for the both in-

put models. Figure 2 shows the initial membership

functions for the ﬁrst input model.

Figure 2: Initial membership functions of ﬁrst input model.

In the training phase, the learning rate taken by

the ﬁrst input model is quite long, with 1100 epochs,

rather than the second input model with only 100

epochs. In addition, the ﬁnal membership functions

of NPI generated by the second input model provide

better interpretability than the ﬁrst input model. Fig-

ure 3 and Figure 4 shows the ﬁnal memberships of the

ﬁrst and second input models, respectively.

After both input models have been trained using

the ANFIS methodology, we perform fuzzy inference

calculations using the testing data as described in Sec-

ICFC 2010 - International Conference on Fuzzy Computation

102

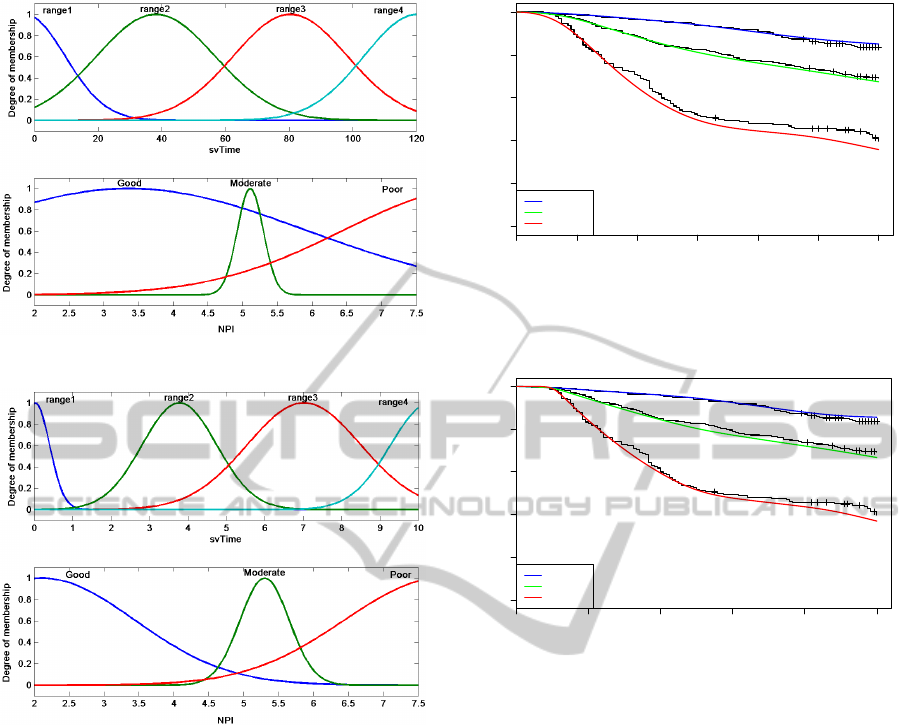
Figure 3: Final membership functions of ﬁrst input model.

Figure 4: Final membership functions of second input

model.

tion 3.2. The output of the testing is the estimation of

conditional failure probability for each time interval

(i.e. the hazard function). From this, the estimation

of survival function using Equation (3) can be plot-

ted. Figure 5 and Figure 6 shows the estimates of

survival function for the ﬁrst input model and second

input model, respectively, against the Kaplan-Meier

plot for the original (observed) data.

It can be seen that, while the ﬁtted-curve obtained

from the second input model are close to Kaplan-

Meier plot for the ‘poor’ category (red line), the ﬁrst

input model produces better a ﬁtted-curve for the

‘moderate’ category (green line). However, both in-

put models gave approximately the same ﬁtted-curve

for the ‘good’ category. It can be seen that, the curves

obtained from the ANFIS model are close to those

of the Kaplan-Meier plot when the NPI value is pre-

sented as a real number.

0 20 40 60 80 100 120

0.0 0.2 0.4 0.6 0.8 1.0

Time(months)

Propotion Surviving

Good

Moderate

Poor

Figure 5: Survival curve of actual Kaplan-Meier (balck

solid lines) estimated against the ﬁrst input model (color

lines).

0 2 4 6 8 10

0.0 0.2 0.4 0.6 0.8 1.0

Time(year)

Propotion Surviving

Good

Moderate

Poor

Figure 6: Survival curve of actual Kaplan-Meier (balck

solid lines) estimated against the second input model (color

lines).

5 CONCLUSIONS

The ANFIS models have been applied to the Notting-

ham Breast Cancer data set with the NPI variable rep-

resented as a real number to estimate the conditional

failure probability and the survival curve. This com-

pares to our previous work, in which the NPI was pre-

sented as a categorical input. Two input models have

been developed and data replication performed in or-

der for the data to used to train an ANFIS model. With

the NPI represented in real values, the ANFIS model

can estimate the proportional hazard rates and, fur-

thermore, the survival function can be plotted.

In general, as ANFIS adapts the neural network

learning, normally before training neural network, it

is necessary to transform the data to new represen-

tation to reduce the dimensionality of input data and

to optimise the generalization performance (Bishop,

2007). In our ﬁndings, when the input variables

span similar ranges or scale, it produces a better in-

terpretability on the ﬁnal membership function with

AN INVESTIGATION OF THE EFFECT OF INPUT REPRESENTATION IN ANFIS MODELLING OF BREAST

CANCER SURVIVAL

103

short learning rate. That is, the results obtained when

representing the time in months differ from those in

which the time is represented in years, despite the fact

this is just a simple scaling.

6 FUTURE WORK

In the future, we aim to investigate how to restrict the

constant value of the singleton output of the rules pro-

ducing by the ANFIS to be all positive, so that we can

obtain a smooth curve of conditional probability with

non-negative values in any of the time intervals.

Further investigations into the effects of scaling

the inputs to the ANFIS model will also be under-

taken, to see whether there are any signiﬁcant effects

on learning rate and/or ﬁnal membership functions.

We also aim to create ANFIS models for other

clinical data sets — we have recently obtained data for

a cohort of over 400 colorectal cancer patients with

ten year follow-up survival data.

ACKNOWLEDGEMENTS

The authors thank all members of the Nottingham

Breast Cancer Pathology Research Group, and par-

ticularly Prof. Ian Ellis, Dr Andy Green and Dr Des

Powe, for their help in preparing and providing the

data set used in this study.

This study was supported by the Ministry of

Higher Learning, Malaysia and Universiti Putra

Malaysia (UPM).

REFERENCES

Biganzoli, E., Boracchi, P., Mariani, L., and Marubini, E.

(1998). Feed forward neural networks for the analysis

of censored survival data: a partial logistic regression

approach. Statistics in Medicine, 17(10):1169–1186.

Bishop, C. M. (2007). Neural Networks for Pattern Recog-

nition. Oxford University Press, UK.

Burke, H., Goodman, P., Rosen, D., Henson, D., Weinstein,

J., Harrell, F., Marks, J., Winchester, D., and Bost-

wick, D. (1997). Artiﬁcial neural network improve

the accuracy of cancer survival prediction. Cancer,

79(4):857–862.

Cancer Research UK (2010). Uk breast cancer incidence

statistics. Date last accessed: 18/05/2010.

Galea, M., Blamey, R., Elston, C., and Ellis, I. (1992). The

nottingham prognostic index in primary breast cancer.

Breast Cancer Research and Treatment, 22(3):207–

219.

Hamdan, H. and Garibaldi, J. M. (2010). Adaptive neuro-

fuzzy inference system (ANFIS) in modelling breast

cancer survival. In 2010 IEEE International Confer-

ence on Fuzzy Systems (FUZZ-IEEE), pages 573–580.

Jang, J.-S. (1993). Anﬁs adaptive-network-based fuzzy in-

ference system. IEEE Transactions on Systems, Man

and Cybernetics, 23(3):665–685.

Joseph, A. C. and David, S. W. (2006). Applications of

machine learning in cancer prediction and prognosis.

Cancer Informatics, 2:59–78.

Lisboa, P. J. G. (2002). A review of evidence of health bene-

ﬁt from artiﬁcial neural networks in medical interven-

tion. Neural Networks, 15(1):11–39.

Mamdani, E. H. and Assilian, S. (1975). An experiment

in linguistic synthesis with a fuzzy logic controller.

International Journal of Man-Machine Studies,, 7:1–

13.

Negnevitsky, M. (2005). Artiﬁcial Intelligence: a guide to

intelligent systems. Pearson Education Limited, Es-

sex, England.

Ramesh, A. N., Kambhampati, C., Monson, J. R. T., and

Drew, P. J. (2004). Artiﬁcial intelligence in medicine.

Annals of The Royal College of Surgeons of England,

86:334–338.

Sugeno, M. (1985). Industrial applications of fuzzy control.

Elsevier Science Pub. Co.

WHO (2010). Cancer. Date last accessed: 18/05/2010.

Yardimci, A. (2009). Soft computing in medicine. Applied

Soft Computing, 9(3):1029 – 1043.

Zadeh, L. A. (1969). Biological application of the theory

of fuzzy sets and systems. In Proceeding of the Inter-

national Symposium of Biocybernetics of the Central

Nervous System, pages 199–212.

ICFC 2010 - International Conference on Fuzzy Computation

104