
NEURAL NETWORK BASED CONTROLLER FOR NONLINEAR
AUTOMATIC GENERATION CONTROL
S. Z. Rizvi, M. S. Yousuf
Department of Electrical Engineering, King Fahd Univ. of Petroleum & Minerals, Dhahran, Saudi Arabia
H. N. Al-Duwaish
Department of Electrical Engineering, King Fahd Univ. of Petroleum & Minerals, Dhahran, Saudi Arabia
Keywords:
Artificial neural network controller, Nonlinear control, Automatic generation control, Load frequency control.
Abstract:
This paper presents an Artificial Neural Network (ANN) based controller design for nonlinear multivariable
systems. The proposed method uses a novel algorithm for using and training a radial basis function (RBF)
neural network based controller. The training algorithm makes sure that it does not violate any constraints on
the inputs or outputs. Trajectory tracking results are presented for the challenging problem of nonlinear single
area Automatic Generation Control (AGC) power system. Both linear and nonlinear cases are considered and
robustness of the controller is tested as well.
1 INTRODUCTION
Artificial neural networks (ANN) have been used for
pattern recognition, function approximation, time-
series prediction and classification problems for quite
some time (Haykin, S., 1999). Owing to their learning
capability, the use of ANN for applications requiring
intelligence, is of no surprise. Hence, like all fields,
researchers working in the field of system theory and
control systems have been attracted to the use and de-
velopment of ANN to solve complex, nonlinear, and
often time varying real life processes. Controlling a
real life process is a task of imminent industrial sig-
nificance and requires effective controller design, that
can steer the process from one operating point to an-
other, keeping in mind all the deterministic as well as
stochastic constraints and limitations on various in-
puts and outputs. The learning properties of neural
networks make them ideal for this purpose.
The use of neural network for controller design
can be found in the literature with different designs
and training techniques. Smith and Boning (Smith,
T. H., Boning, D. S., 1997) proposed a self-tuning
EWMA adaptive controller which, according to the
authors was able to replace an experienced engineer
needed to tune the controller. Thapa, Jones, and Zhu
proposed a scheme for combining back propagation
trained neural network with self tuning regulator tech-
niques (Thapa, B. K., Jones, B., Zhu, Q. M., 2000).
Other efforts to solve control problems using ANN
include, but are not limited to those of (Shukla, D.,
Dawson, D. M., Paul, F. W., 1999; Lu, J., Yahagi, T.,
2000; Hayakawa, T., Haddad, W., Hovakimyan, N.,
2000; Yang, Y., Wang, X., 2007; Hayakawa, T., Had-
dad, W., Volyanskyy, K. Y., 2008; Zayed, A. S., Hus-
sain, A., Abdullah, R. A., 2006; Petre, E., Selisteanu,
D., Sendrescu, D., 2008; Cong, S., Liang, Y., 2009),
and (Al-Duwaish, H. N., Rizvi, S. Z., 2010).
Power systems play a vital role in our lives, en-
suring proper generation, distribution, conservation,
recycling and regeneration of power for domestic as
well as commercial life. Power systems can safely be
regarded as the backbone of every industry. Hence,
proper control of power systems is an extremely im-
portant task and calls for accelerated efforts from
researchers all over the world (Shijie, Y., Xu, W.,
2009). This paper presents a new neural network
based controller design for nonlinear multivariable
systems. The design uses radial basis function (RBF)
neural network as controller. Output layer synaptic
weight are updated and weight update equations us-
ing classical least mean square (LMS) principle is de-
rived for the RBF network. Because of remarkable
adaptation properties of neural networks, the derived
322
Z. Rizvi S., S. Yousuf M. and N. Al-Duwaish H..
NEURAL NETWORK BASED CONTROLLER FOR NONLINEAR AUTOMATIC GENERATION CONTROL.
DOI: 10.5220/0003081503220329
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
322-329
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

controller is robust to accommodate parameter vari-
ations, if any, as well. The developed controller is
tested by employing it to control frequency deviation
caused by changes in loading in a power generator.
This problem is known as Load Frequency Control
(LFC) or Automatic Generation Control (AGC), and
has been an important control problem for power en-
gineers owing to its significance in daily life.
Notations in this paper are used in the follow-
ing manner. Variables in lower case represent scalar
quantities. Lower case bold variables represent vector
quantities. Upper case bold variables represent matri-
ces. The only exceptions to this convention is in the
choice of a more conventional J for the cost function,
and where notations are defined otherwise, as in the
AGC model. The paper is arranged as follows. Sec-
tion 2 takes a detailed look at the development and
training algorithm of the proposed controller. Section
3 takes a look at the power system model and defines
the AGC control problem in detail. Simulation re-
sults for the AGC problem are presented in section 4.
Finally, conclusions are drawn and recommendations
for future work are provided in section 5.
2 CONTROLLER DESIGN
Consider a multi-input multi-output nonlinear process
having p inputs and m outputs shown in Figure 1. It is
required that the process outputs follow a desired set
of reference points r(t) = [r
1
(t)· ··r
m
(t)]. The process
is approximated using a linear time-invariant (LTI)
model. This can be achieved in terms of offline sys-
tem identification. The linearized approximation can
be expressed as
x(t + 1) = Ax(t) + Bu(t),
y(t) = Cx(t) + Du(t). (1)
The controller consists of an RBF nerual network.
The j
th
output of the RBF network is given by
v
j
(t) = w
j
φ
T
(t), (2)
where w
j
is the vector for weights of j
th
RBF output,
given by
w
j
= [w
1j
···w
qj
], (3)
and φ(t) is the basis function vector which is given by
φ(t) = [φ(kr(t) − c
1
k)···φ(kr(t) − c
q
k)]. (4)
In the above equations, q denotes the number of neu-
rons in the hidden layer, c
i
is the center vector for
the i
th
neuron of that layer, φ is the radial basis func-
tion, and k.k denotes norm. RBF networks enjoy sev-
eral advantages over multi-layer perceptrons (MLP)s
in that RBF networks consist of only one hidden layer
as opposed to multiple layers in MLPs. Hence, the
learning time of RBF networks is much less as com-
pared to MLPs. RBF networks are also called univer-
sal approximators (Haykin, S., 1999), and hence can
approximate any continuous nonlinear function. It is
this property of RBF neural networks that has moti-
vated the authors to choose it for controller design.
RBF network can compensate for the nonlinearity in
the process, and hence can control the process using
linearized model for updating its weights.
For j = 1, 2,··· p, the constraints on any control
signal u
j
(t) are given by
u
min
≤ u
j
(t) ≤ u
max
.
To meet this constraint, the output of the RBF net-
work is transformed by a tangent-sigmoid activation
function forming the constrained control signal
u
j
(t) = α
e
kv
j
(t)
− 1
e
kv
j
(t)
+ 1
= α
e
kw
j
φ(t)
− 1
e
kw
j
φ(t)
+ 1
,
where α = |u
min
| = |u
max
| denotes the upper and lower
limits of the constraints and k is used to adjust the
slope of the linear part of tangent-sigmoid function.
The difference between the reference point r(t)
and the process output
ˆ
y(t) gives the error e(t) =
[e
1
(t)· ··e
m
(t)]
T
. In order to update the controller, a
cost function J is sought to be minimized.
J = e
T
(t)e(t). (5)
The RBF output layer weights are updated in the neg-
ative direction of the gradient of J. This approach,
known as the classical Least Mean Square principle is
a ‘sensible’ choice for training RBF networks accord-
ing to (Haykin, S., 1999). Hence, the weight update
equation for j
th
control signal u
j
(t) is given in equa-
tion (6) as
w
j
(k+ 1) = w
j
(k) − η
∂J
∂w
j
. (6)
Now finding the partial derivative of J w.r.t w
j
∂J
∂w
j
= 2e
T
(t)
∂
∂w
j
e(t)
= 2e
T
(t)
∂
∂w
j
(r(t) −
ˆ
y(t))
= −2e
T
(t)
∂
∂w
j
ˆ
y(t)
= −2e
T
(t)
∂
∂w
j
(Cx(t) + Du(t)),
NEURAL NETWORK BASED CONTROLLER FOR NONLINEAR AUTOMATIC GENERATION CONTROL
323
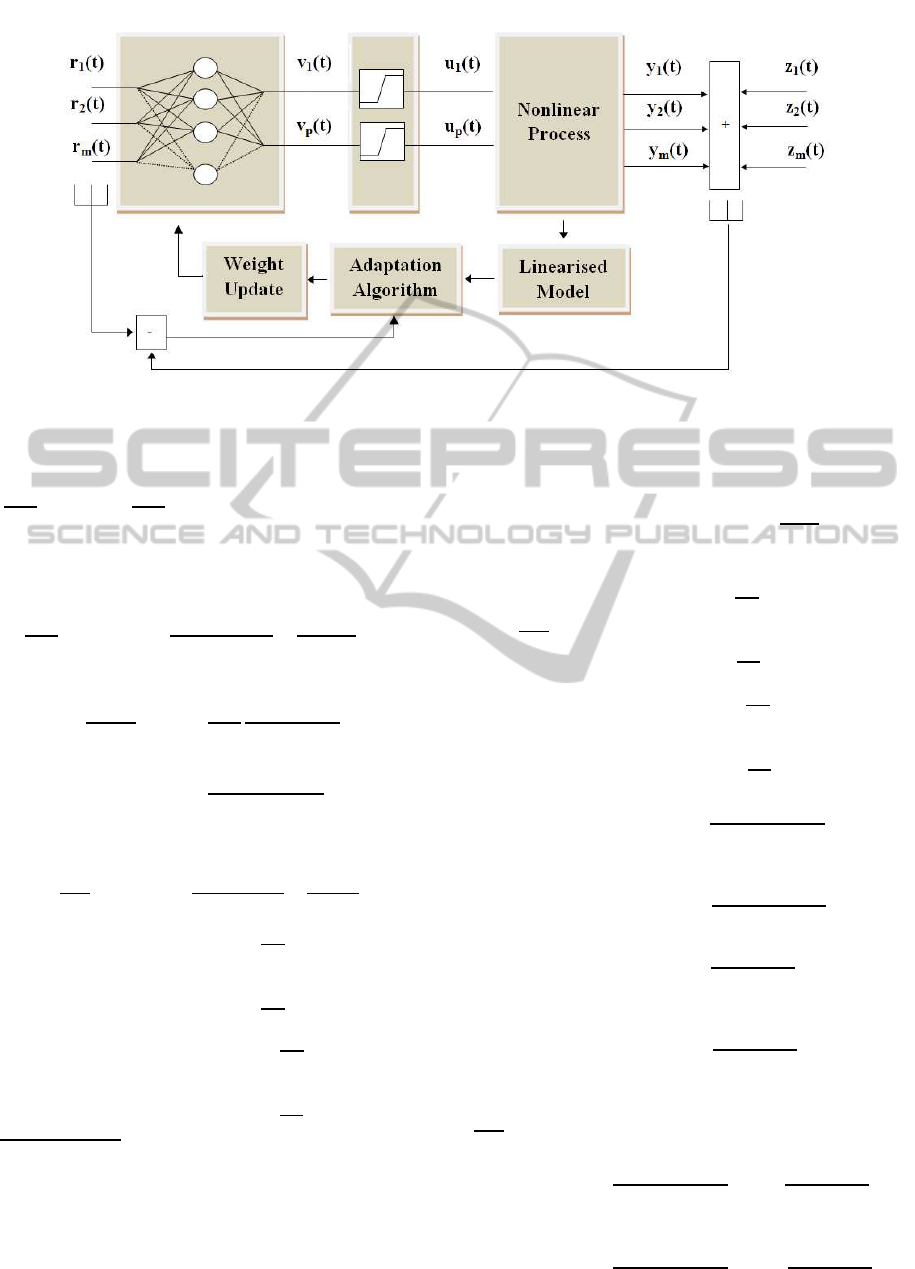
Figure 1: Neural network based controller for nonlinear MIMO systems. Parameters z
i
(t) indicate output additive noise at the
i
th
output.
which can be written as
1
∂J
∂w
j
= −2e
T
(t)
∂
∂w
j
(C{Ax(t − 1) + Bu(t − 1)}
+Du(t)).
The terms independent of w
j
would vanish,
∂J
∂w
j
= −2e
T
(t)
∂CBu(t − 1)
∂w
j
+
∂Du(t)
∂w
j
. (7)
Finding the derivative of tangent-sigmoid function
∂u
j
(t)
∂w
j
= α
∂
∂w
j
e
kw
j
φ(t)
− 1
e
kw
j
φ(t)
+ 1
= α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+ 1)
2
. (8)
Equation 7 can now be written as
∂J
∂w
j
= −2e
T
(t)
CB∂u(t −1)
∂w
j
+
D∂u(t)
∂w
j
(9)
= −2e
T
(t)
ψ
11
·· ·ψ
1p
.
.
.
.
.
.
.
.
.
ψ
m1
·· ·ψ
mp
∂
∂w
j
u
1
(t −1)
.
.
.
∂
∂w
j
u
p
(t − 1)
+
d
11
·· ·d
1p
.
.
.
.
.
.
.
.
.
d
m1
·· ·d
mp
∂
∂w
j
u
1
(t)
.
.
.
∂
∂w
j
u
p
(t)
, (10)
1
Since x(t − 1) depends on u(t − 2) which in turn is a
function of w, the dependence of state vector x(t − 1) on
the weights w of the neural network is acknowledged. How-
ever the term for derivative of CAx(t − 1) w.r.t w is deliber-
ately neglected since expansion of x(t) into past state terms
Ax(t − n) + Bv(t − n) for n ≥ 2 does not yield significant
improvement on controller result.
where Ψ ε ℜ
m×p
is the product of C ε ℜ
m×n
and B
ε ℜ
n×p
. The derivative of all terms except u
j
(t − 1)
and u
j
(t) would vanish. Substituting
∂u
j
(t)
∂w
j
from the
derivative equation 8,
∂J
∂w
j
= −2e
T
(t)
ψ
1j
∂
∂w
j
u
j
(t −1)
.
.
.
ψ
mj
∂
∂w
j
u
j
(t −1)
+
d
1j
∂
∂w
j
u
j
(t)
.
.
.
d
mj
∂
∂w
j
u
j
(t)
(11)
= −2e
T
(t)
ψ
1j
α
2kφ(t−1)e
kw
j
φ(t−1)
(e
kw
j
φ(t−1)
+1)
2
.
.
.
ψ
mj
α
2kφ(t−1)e
kw
j
φ(t−1)
(e
kw
j
φ(t−1)
+1)
2
+
d
1j
α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+1)
2
.
.
.
d
mj
α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+1)
2
(12)
∂J
∂w
j
= −2[e
1
(t)·· ·e
m
(t)] (13)
ψ
1j
α
2kφ(t−1)e
kw
j
φ(t−1)
(e
kw
j
φ(t−1)
+1)
2
+ d
1j
α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+1)
2
.
.
.
ψ
mj
α
2kφ(t−1)e
kw
j
φ(t−1)
(e
kw
j
φ(t−1)
+1)
2
+ d
mj
α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+1)
2
ICFC 2010 - International Conference on Fuzzy Computation
324

= 2e
1
(t)
ψ
1j
α
2kφ(t − 1)e
kw
j
φ(t−1)
(e
kw
j
φ(t−1)
+ 1)
2
+ d
1j
α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+ 1)
2
!
·· ·−2e
m
(t)
ψ
mj
α
2kφ(t − 1)e
kw
j
φ(t−1)
(e
kw
j
φ(t−1)
+ 1)
2
+ d
mj
α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+ 1)
2
!
.
(14)
Finally, the weight update equation for j
th
control
signal u
j
(t) becomes
w
j
(k+ 1) = w
j
(k) + 2η
m
∑
l=1
e
l
(t)
ψ
l j
α
2kφ(t − 1)e
kw
j
φ(t−1)
(e
kw
j
φ(t−1)
+ 1)
2
+ d
l j
α
2kφ(t)e
kw
j
φ(t)
(e
kw
j
φ(t)
+ 1)
2
!
.
(15)
where e
l
(t) corresponds to error at the l
th
output, ψ
l j
is the element at the l
th
row and j
th
column of the
matrix Ψ, η is the learning rate of the RBF neural
network, w
j
is the vector for the weights of j
th
RBF
output, m is the number of outputs of the process, and
φ(t) is the basis function vector.
3 THE AUTOMATIC
GENERATION CONTROL
PROBLEM
Automatic Generation Control (AGC) has been an
important subject for power engineers for quite some
time. It is also known as Load Frequency Control
(LFC) and has been under study for decades. The
problem arises from the fact that loading in power
systems is never constant, and changes in load in-
duce changes in system frequency. This is because
imbalance between real generated power and loading
causes the generator shaft speed to change, resulting
in the variation of system frequency.
Hence, a controller is needed to keep the fre-
quency of the output electrical power at the nominal
value. The input mechanical power to the generator is
used to control the load frequency. The main qual-
ity risk involved during control is that control area
frequencies can undergo prolonged fluctuations due
to a sudden change of loading in an interconnected
power system as described in (Chan, W. C., Hsu, Y.
Y., 1981). These prolonged fluctuations are mainly
the result of system nonlinearities. The purpose of
AGC is to track load variations and reduce these fluc-
tuations. In this way, the system frequency is main-
tained, transient errors are minimized and steady state
error is avoided.
Linear and nonlinear control of AGC systems has
been studied by several researchers as in (Pan, C. T.,
Liaw, C. M., 1989; Wang, Y., Zhou, R., Wen, C.,
1993). AGC systems are modeled with nonlineari-
ties, one of the main type of which is the Generation
Rate Constraint (GRC) (Velusami, S., Chidambaram,
I. A., 2007). This is the constraint on the power
generation rate of the turbine and due to it the dis-
turbance in one area affects the output frequency in
other interconnected areas. Variable Structure Con-
trol (VSC) based techniques, (Al-Hamouz, Z. M., Al-
Duwaish, H. N., 2000), (Wang, Y., Zhou, R., Wen,
C., 1993) and Model Predictive Control (MPC) based
techniques (Yousuf, M. S., Al-Duwaish, H. N., Al-
Hamouz, Z. M., 2010), (Kong, L., Xiao, L., 2007)
have been applied to AGC and an excellent literature
survey is given in (Shayeghi, H., Shayanfar, H. A.,
Jalili, A., 2009).
3.1 AGC System Model
The block diagram of an AGC system is given in Fig-
ure 2 and the states of the system are:
˙
X =
∆
˙
f
i
(t)∆
˙
P
g
i
(t)∆
˙
X
g
i
(t)∆
˙
P
c
i
(t)∆
˙
P
t
i
(t)
T
. (16)
The definitions of the symbols used in the model
are as follows:
f
i
: area frequency in ith area (Hz).
P
gi
: generator output for ith area (p.u. MW).
X
gi
: governor valve position for ith area (p.u.
MW).
P
ci
: integral control value for ith area (p.u. MW).
P
ti
: tie line power output for ith area (p.u. MW).
P
ti
: load disturbance for ith area (p.u. MW).
T
gi
: governor time constant for ith area (s).
T
pi
: plant model time constant for ith area (s).
T
ti
: turbine time constant for ith area (s).
K
pi
: plant transfer function gain for i
t
h area.
R
i
: speed regulation due to governor action for ith
area (Hz p.u. MW
−1
).
B
i
: frequency bias constant for ith area (p.u. MW
Hz
−1
).
a
ij
: ratio between the base values of areas i and j.
The model can be generally represented by the fol-
lowing equations:
˙
X
i
(t) = A
i
x
i
(t) + B
i
u
i
(t)+
n
∑
j=1, j6=i
E
ij
x
j
(t) + F
i
d
i
(t), (17)
y
i
(t) = C
i
(t)x
i
(t), (18)
NEURAL NETWORK BASED CONTROLLER FOR NONLINEAR AUTOMATIC GENERATION CONTROL
325
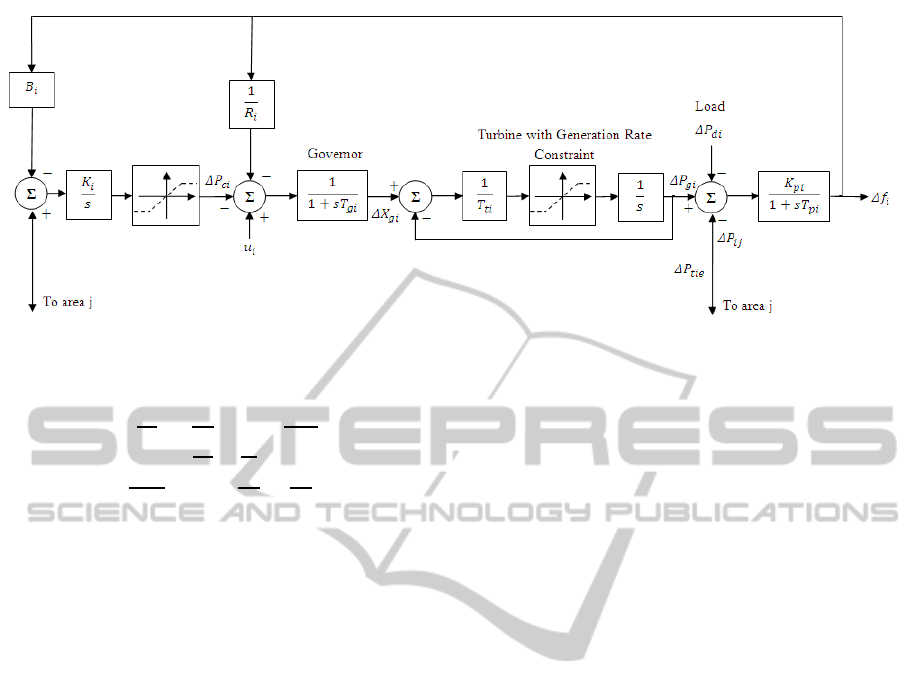
Figure 2: Block diagram of n
th
area AGC with GRC nonlinearities.
where
A
i
=
−1
T
p
i
K
p
i
T
p
i
00
−K
p
i
T
p
i
0
−1
T
t
i
1
T
t
i
0 0
−1
R
i
T
G
i
0
−1
T
G
i
−1
T
G
i
0
K
E
i
0 0 0 K
E
i
∑
j
T
ij
0 0 0 0
,(19)
where K
E
i
is zero for single area machine.
B
T
i
=
0 0 1/T
G
i
0 0
, (20)
E
ij
=
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
−T
ij
0 0 0 0
, (21)
F
T
i
=
−K
p
i
/T
p
i
0 0 0 0
, (22)
d
i
(t) = P
d
i
(t). (23)
The numerical values of these parameters are
given in Section 4. The control objective of AGC is to
keep the change in frequency, ∆ f
i
(t) = x
1
(t) as close
to 0 as possible in the presence of load disturbance,
d
i
(t) by the manipulation of the input, u
i
(t). The de-
tailed model of the system along with the values of
state matrices can be found in (Yang T. C., Cimen,
H., Zhu, Q. M., 1998).
3.2 Control Objective
Given a linear or nonlinear AGC system, the con-
troller objective is to construct the ANN based con-
troller such that it minimizes the error in the minimum
time using minimum effort in the presence of distur-
bances and constraints.
The disturbance is applied as a p.u. load demand.
Practically, this translates to a step load demand of a
certain percentage from the AGC system. Naturally,
this demand will cause the system to adjust its load
by the same amount to fulfil the quality of service.
This will change the load frequency. The proposed
controller is required to minimize this frequency de-
viation and bring it to zero in minimum time while
obeying the constraints on system states and control
signal.
4 SIMULATION RESULTS
Linear as well as the nonlinear control for a single
area AGC system is simulated. The system is sim-
ulated as a single-input single-output (SISO) system,
with one control signal being the input and frequency
deviation being the output. The cost function is given
by
J = e
T
(t)e(t)
= kr(t) −
ˆ
y(t)k
2
,
where r(t) denotes reference values for frequency de-
viation, which is zero for the given control objective.
The vector
ˆ
y(t) denotes the actual AGC output values
of these parameters. The AGC parameters are com-
puted using the following values:
T
p
= 20s, K
p
= 120 Hz p.u. MW
−1
, T
t
= 0.3s, T
g
= 0.08s, R = 2.4 Hz p.u. MW
−1
, T
s
= 0.05s, where
T
s
refers to discretization sampling time. The corre-
sponding values of A, B & F are:
A =
−0.05 6 0 0
0 −3.33 3.33 0
−5.208 0 −12.5 −12.5
0.6 0 0 0
, (24)
B =
0 0 12.5 0
T
, (25)
F =
−6 0 0 0
T
. (26)
ICFC 2010 - International Conference on Fuzzy Computation
326
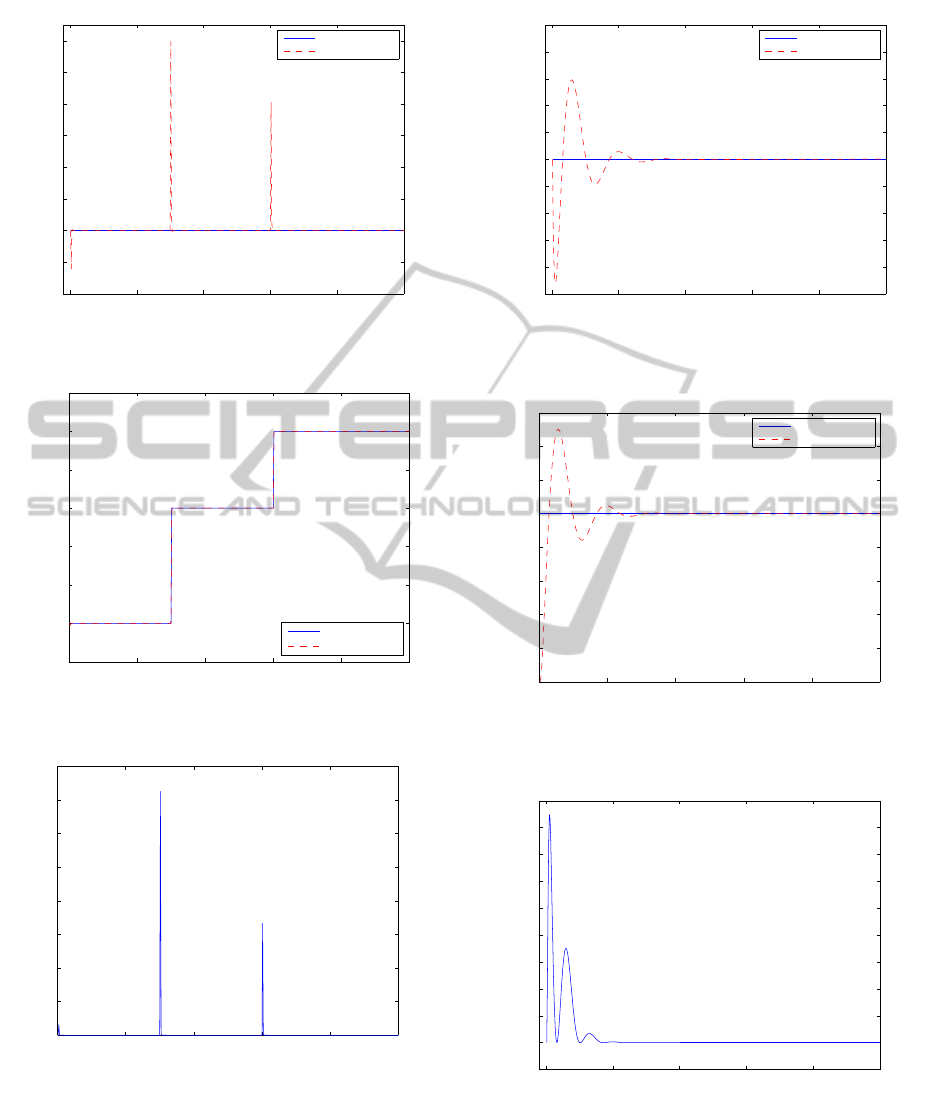
0 5 10 15 20 25
−4
−2
0
2
4
6
8
10
12
x 10
−3
time(sec)
state x
1
reference signal
controlled output
Figure 3: Frequency deviation for linear AGC.
0 5 10 15 20 25
−0.01
0
0.01
0.02
0.03
0.04
0.05
0.06
time(sec)
x
2
load disturbance
generated power
Figure 4: Change in generated power for linear AGC.
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
x 10
−5
time(sec)
mse
Figure 5: Convergence of error function for linear AGC.
While designing a controller, a suitable number of
neurons can be chosen based on experience. Repeated
simulations can then be run to test the controller with
increased number of neurons each time until no ap-
preciable increase in performance is noted. To begin
with, a network of just two RBF neurons is used for
0 5 10 15 20 25
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
time(sec)
state x
1
reference signal
controlled output
Figure 6: Frequency deviation for AGC with GRC nonlinear-
ity.
0 5 10 15 20 25
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
0.016
time(sec)
x
2
load disturbance
generated power
Figure 7: Change in generated power for AGC with GRC non-
linearity.
0 5 10 15 20 25
−0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
time(sec)
mse
Figure 8: Convergence of error Function for AGC with GRC
nonlinearity.
controller design. The input to the neural network is
the reference signal for frequency deviation. A neu-
ron center for each neuron is chosen around the desi-
NEURAL NETWORK BASED CONTROLLER FOR NONLINEAR AUTOMATIC GENERATION CONTROL
327

red set-point on the reference trajectory. Spread of the
gaussian basis function σ is chosen such that the RBF
functions are neither too peaked nor too flat. Methods
to find proper basis function spread exist in (Haykin,
S., 1999). A nominal spread of 0.04 is chosen. The
learning rate η has to be chosen with care as well.
Small value of learning rate can cause slow conver-
gence of error while too large a value can make the
controller unstable.
The constraint α = |u
min
| = |u
max
| on the control
signal is given by
−0.5 ≤ α ≤ 0.5.
Single area linear and nonlinear AGC is simulated
with zero initial conditions and the neural network
controller shows satisfactory control results for both
cases.
4.1 Single Area AGC excluding
Nonlinearities
First, the nonlinearity is excluded and the perfor-
mance of the proposed controller is tested for the lin-
ear system.
To study the robustness of the proposed controller,
a condition of varying load disturbance is considered.
The load is simulated to vary from a disturbance of
0 p.u. to 0.03 p.u. after 7.5 seconds, and then going
up to 0.05 p.u. after 15 seconds. This directly affects
the load frequency as seen in Figure 3. It is seen that
the load frequency varies most when the disturbance
varies most, but the neural network controller quickly
pushes it back zero. The corresponding behavior of
the change in generated power is seen in the Figure
4. It is seen that the change in generated power fol-
lows the load disturbance as well, meaning that the
system can supply the load its power demand. The
power generated changes most when the disturbance
is largest. The error convergence is given in Figure 5.
4.2 Single Area AGC including GRC
Nonlinearities
Now the case of nonlinear AGC system is considered.
The nonlinearities in the system appear in the form of
saturation on change of states x
2
and x
4
as illustrated
in Figure 2. Mathematically, the nonlinearity can be
described as
x
i
(t − 1) − GRC ≤ ∆x
i
(t) ≤ x
i
(t − 1) + GRC,
for i = 2,4
The system is tested for a practical GRC value of 0.6
p.u. MW min
−1
= 0.01 p.u. MW sec
−1
, as done
in previous work of (Wang, Y., Zhou, R., Wen, C.,
1993). This means that the generated power output of
the system cannot vary by more than 0.01 p.u. MW in
1 second. A disturbance of 1% p.u. is present in the
system. The proposed controller is applied to the sys-
tem with this nonlinearity and the results can be seen
in Figures 6, 7, and 8. The NN controller successfully
keeps the frequency deviation to zero while the Gen-
erated power follows the step change in load demand
disturbance.
5 CONCLUSIONS
A new and efficient ANN based control scheme is
designed. Weight update algorithm is worked out
and the controller is shown to be viably applicable to
practical power systems. The dynamical behavior of
the single nonlinear AGC system with proposed con-
troller is examined. The proposed controller performs
well for linear as well as nonlinear case. With just
two neurons, the performance of the controller is well
acceptable under rapid load variations. Encouraging
results are a sound motivation for possible future ap-
plication of proposed controller to multiple area linear
and nonlinear AGC problem.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the support
of King Fahd University of Petroleum & Minerals,
Dhahran, Saudi Arabia.
REFERENCES
Al-Duwaish, H. N., Rizvi, S. Z. (2010). Neural network
based controller for constrained multivariable sys-
tems. In 12th WSEAS Conference on Automatic Con-
trol, Modelling and Simulation ACMOS 2010, Italy,
pages 104–109.
Al-Hamouz, Z. M., Al-Duwaish, H. N. (2000). A new load
frequency variable structure controller using genetic
algorithms. In Electric Power Systems Research. vol-
ume 55, no. 1, pages 1-6.
Chan, W. C., Hsu, Y. Y. (1981). Automatic generation
control of interconnected power system using variable
structure controllers. In Proceedings of the IEE Part
C. volume 128, no. 5, pages 269-279.
Cong, S., Liang, Y. (2009). Pid-like neural network nonlin-
ear adaptive control for uncertain multivariable mo-
tion control systems. In IEEE Transaction on Indus-
trial Electronics. volume 56, no. 10, pages 288-292.
ICFC 2010 - International Conference on Fuzzy Computation
328

Hayakawa, T., Haddad, W., Hovakimyan, N. (2000). Neu-
ral network adaptive control for nonlinear uncertain
dynamical systems with asymptotic stability guaran-
tees. In IEEE American Control Conference, 2005,
USA. pages 1301-1306.
Hayakawa, T., Haddad, W., Volyanskyy, K. Y. (2008). Neu-
ral network hybrid adaptive control for nonlinear un-
certain impulsive dynamical systems. In Nonlinear
Analysis: Hybrid Systems. pages 862-874.
Haykin, S. (1999). Neural Networks - A Comprehensive
Foundation. Prentice-Hall, Second Edition.
Kong, L., Xiao, L. (2007). A new model predictive con-
trol scheme-based load-frequency control. In IEEE
International Conference on Control and Automation.
volume 1, pages 2514-2518.
Lu, J., Yahagi, T. (2000). Application of neural networks to
nonlinear adaptive control systems. In IEEE Interna-
tional Cconference on Signal Processing, ICSP, 2000.
pages 252-257.
Pan, C. T., Liaw, C. M. (1989). An adaptive controller
for power system and load frequency control. In
IEEE Transactions on Power Systems. volume 4, no.
1, pages 122-128.
Petre, E., Selisteanu, D., Sendrescu, D. (2008). Neural net-
works based adaptive control for a class of time vary-
ing nonlinear processes. In IEEE International Con-
ference on Control, Automation and Systems, ICCAS,
2008, Korea. pages 1355-1360.
Shayeghi, H., Shayanfar, H. A., Jalili, A. (2009). Load fre-
quency control strategies: A state-of-the-art survey for
the researcher. In Energy Conversion and Manage-
ment. volume 50, no. 1, pages 344-353.
Shijie, Y., Xu, W. (2009). Rbf neural network adaptive con-
trol of microturbine. In IEEE Global Congress on In-
telligent Systems. pages 288-292.
Shukla, D., Dawson, D. M., Paul, F. W. (1999). Mul-
tiple neural-network-based adaptive controller using
orthonormal activation function neural networks. In
IEEE Transaction on Neural Networks. volume 10,
no. 6, pages 1494-1501.
Smith, T. H., Boning, D. S. (1997). A self-tuning ewma
controller utilizing artificial neural network function
approximation techniques. In IEEE Transaction on
Components, Packaging, and Manufacturing Technol-
ogy, Part C. volume 20, no. 2, pages 121-132.
Thapa, B. K., Jones, B., Zhu, Q. M. (2000). Non-linear
control with neural networks. In Fourth International
Conference on knowledge-based Intelligent Engineer-
ing Sys. & Allied Tech., 2000, U.K. pages 868-873.
Velusami, S., Chidambaram, I. A. (2007). Decentralized bi-
ased dual mode controllers for load frequency control
of interconnected power systems considering gdb and
grc non-linearities. In Energy Conversion and Man-
agement.
Wang, Y., Zhou, R., Wen, C. (1993). Robust load frequency
controller design for power systems. In IEE Proceed-
ings Part C. volume 140, no. 1, pages 11-16.
Yang T. C., Cimen, H., Zhu, Q. M. (1998). Decentralised
load-frequency controller design based on structured
singular values. In IEE Proceedings on Generation,
Transmission and Distribution. volume 145, no. 1,
pages 7-14.
Yang, Y., Wang, X. (2007). Adaptive h
∞
tracking control
for a class of uncertain nonlinear systems using radial-
basis-function neural networks. In Neurocomputing.
volume 70, pages 932-941.
Yousuf, M. S., Al-Duwaish, H. N., Al-Hamouz, Z. M.
(2010). PSO based predictive nonlinear automatic
generation control. In 12th WSEAS Conference on Au-
tomatic Control, Modelling and Simulation ACMOS
2010, Italy, pages 87–92. In Press.
Zayed, A. S., Hussain, A., Abdullah, R. A. (2006). A novel
multiple-controller incorporating a radial basis func-
tion neural network based generalized learning model.
In Neurocomputing. volume 69, pages 1868-1881.
NEURAL NETWORK BASED CONTROLLER FOR NONLINEAR AUTOMATIC GENERATION CONTROL
329
