USING SLOW FEATURE ANALYSIS TO IMPROVE

THE REACTIVITY OF A HUMANOID ROBOT’S

SENSORIMOTOR GAIT PATTERN

Sebastian H

ofer and Manfred Hild

Neurorobotics Research Laboratory, Computer Science Department, Humboldt-Universit

at zu Berlin, Berlin, Germany

Keywords:

Slow feature analysis, Biped walking, Volterra ﬁlters, Recurrent neural networks, Sensorimotor control, Hu-

manoid robotics.

Abstract:

This paper presents an approach for increasing the reactivity of a humanoid robot’s gait, incorporating Slow

Feature Analysis (SFA), an unsupervised learning algorithm issuing from the domain of theoretical biology.

The main objective of this work is to ﬁnd a means to detect disturbances in the gait pattern at an early stage

without losing stability. Another goal is to investigate the general potential of SFA for using it within sen-

sorimotor loops which to our knowledge has not been considered until now. The application of SFA within

sensorimotor loops is motivated by pointing out its relation to second-order Volterra ﬁlters. Our experiments

show that the overall reactivity of the gait pattern increases without any profound loss in stability, and that

SFA appears to be suitable for the usage even at such levels of sensorimotor control that are directly involved

into motor activity regulation.

1 INTRODUCTION

Recent trends in cognitive robotics stipulate new prin-

ciples for designing intelligent systems, amongst oth-

ers ecological balance in the complexity of the sen-

sory, motor and neural systems of the agent (Pfeifer

and Bongard, 2006). In order to develop autonomous

robots that are able to learn advanced behaviours, par-

ticularly if they are presumed to learn in a fairly un-

supervised manner, we expect the integration of re-

dundantly covered sensory data channels to be inde-

spensable for better and stable control mechanisms.

For we are dealing with real hardware and a greatly

intricate real world environment, ably integration of

high-dimensional sensory data may increase stability

and adaptivity without losing the reactivity of the dy-

namical system formed by the robot and its environ-

ment.

On the other hand, the integration of multi-

dimensional sensory data streams asks for means to

extract useful information in a computationally ef-

ﬁcient manner. Slow Feature Analysis (SFA), the

method applied in this paper is a promising candi-

date that may fulﬁll the forementioned constraints and

needs.

SFA is an unsupervised learning algorithm issuing

from the domain of theoretical biology. It was develo-

ped in order to ﬁnd a method for learning and extract-

ing invariances from visual data, exploiting the idea

of temporal slowness (also called temporal stability,

see e.g., (Wyss et al., 2006)), assuming that high-level

abstract features of the input signal vary slowly over

time. SFA can deal with high-dimensional data, for

it is based on the generalised eigenvalue problem, for

which fast and reliable algorithms exist. By applying

SFA to visual data, it could be shown that temporal

slowness is an important learning principle, yielding

structures that resemble cells found in the primary vi-

sual cortex and the hippocampus (Berkes and Wiskott,

2002; Franzius et al., 2007). Besides, the algorithm’s

capability to detect and extract driving forces from

non-stationary time-series (Wiskott, 2003) as well as

its use for pattern recognition (Berkes, 2006) have

been investigated.

In a recent paper, we have successfully shown

that SFA can handle many kinds of sensory qualities

by applying it to abstract visual features, accelera-

tion sensor and motor position data from humanoid

robots (Spranger et al., 2009). SFA extracted mean-

ingful components from the multisensory input data

stream, which were employed for detecting and clas-

sifying postures of humanoid robots.

In this article we demonstrate how SFA can be

used to increase the reactivity of a biped gait pattern

212

Höfer S. and Hild M..

USING SLOW FEATURE ANALYSIS TO IMPROVE THE REACTIVITY OF A HUMANOID ROBOT’S SENSORIMOTOR GAIT PATTERN.

DOI: 10.5220/0003082102120219

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages

212-219

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

provided for a humanoid robot platform. The gait pat-

tern is neuronally implemented and based on a senso-

rimotor loop. Although the walking pattern is gen-

erally stable, robots tend to fall to the ground when

walking on surfaces with a high grip, such as carpets

or natural surfaces. Thus, a mechanism to detect when

the gait becomes unstable is needed. One of the main

problems is that the fraction of time to avoid a col-

lision with the ground or at least alleviate its effects

is very short. However, in general both high stability

and reactivity cannot be easily achieved at the same

time. We show that SFA applied to a time embedded

signal is formally equivalent to a so-called Volterra

ﬁlter, and use SFA to learn the ﬁlter weights in an un-

supervised manner. The result is a highly reactive ﬁl-

ter, which is incorporated into the sensorimotor con-

trol loop that generates the movement, decreasing the

response time of the dynamical system formed by the

robot and its environment, and consequently provid-

ing means for a robust fall detection and prevention.

To our knowledge this is the ﬁrst attempt to use

SFA components for robot control, so that the pre-

sented work also constitutes a proof of concept for

the successful application of SFA within sensorimo-

tor loops.

The remaining paragraphs will cover the follow-

ing topics: We begin with a short introduction to the

Slow Feature Analysis and Volterra ﬁlters, pointing

out why quadratic ﬁlters are a well-motivated choice

for our purposes. Next, we pass over to the experi-

ments section, presenting the robot platform that was

used for our experiments, and describe the examined

gait pattern and our modiﬁcations to it. In the last

section we present our results and show that the mod-

iﬁcations performed prove useful for increasing the

robots reactivity without destabilisation of the gait.

We conclude this article with a summary of the ob-

tained results and by giving insights into future work.

2 METHODS

In this section we ﬁrst give a brief introduction to the

Slow Feature Analysis (SFA) algorithm and its math-

ematical foundations. Then, we show that SFA yields

a solution that is formally equivalent to second-order

Volterra ﬁlters with ﬁnite kernel. In a later section, we

will exploit this relationship when we train an equiv-

alent structure by means of a supervised learning al-

gorithm and compare the obtained results.

2.1 Slow Feature Analysis

Slow Feature Analysis is an unsupervised learning

algorithm that attempts to solve a particular opti-

misation problem related to temporal slowness (see

(Wiskott, 1998) for the original publication and

(Wiskott and Sejnowski, 2002) for a more extensive

introduction). The aim of the algorithm is to extract

slowly changing features from a multi-dimensional

input signal which vary over a short time scale.

The learning problem can be stated as follows:

Given a potentially multidimensional input signal

x(t) = [x

, .., x

]

, N being the dimensionality of the

input, the algorithm searches for input-output func-

tions g

(x), j ∈ J that determine the output of the sys-

tem y

(t) := g

(x(t)). The objective function is given

∆(y

) := h ˙y

is minimal (1)

where h·i

signiﬁes the average over time and ˙y is the

derivative

of y. The equation speciﬁes the intended

learning problem of temporal stability, i.e., ∆(y

) is

minimal if y

varies slowly over time. However, every

constant function would easily fulﬁll this restriction,

so three additional constraints are formulated:

= 0 (zero mean) (2)

= 1 (unit variance) (3)

∀i < j hy

= 0 (decorrelation) (4)

Equation 3 forces the output signal to carry informa-

tion. Equation 4 requires the set of output functions to

be decorrelated and therefore to carry different infor-

mation and to not simply reproduce each other. It also

induces an ordering on the output signals, i.e., the ﬁrst

signal y

will be slowest one, while the next signal y

will be less optimal, etc.

Since the above stated optimisation problem is

in general hard to solve, SFA provides a solution to

learning the real valued functions g

by simplifying

the problem: The input-output functions g

are con-

strained to be linear combinations of a ﬁnite set of ba-

sis functions. Let the input signal be x = [x

, .., x

]

then the input-output function g = [g

(x), ..., g

(x)]

can be deﬁned as the weighted sum of K basis func-

tions h = [h

, .., h

]

, yielding

= g

(x) :=

∑

k=1

(x). (5)

In the linear case no speciﬁc basis functions are

used and the input-output functions compute as the

The derivative is approximated by a ﬁnite difference

˙x(t) := x(t) − x(t − 1) for we are dealing with discrete sig-

nals.

USING SLOW FEATURE ANALYSIS TO IMPROVE THE REACTIVITY OF A HUMANOID ROBOT'S

SENSORIMOTOR GAIT PATTERN

213

weighted sum of the input data; this application is

called SFA(1) or linear SFA. In order to deal with

nonlinearities in the input data the basis functions are

chosen to be a polynomial, usually quadratical, ex-

pansion of the input, leaving the weight vectors w

be learnt. This technique is similar to the so-called

kernel trick (Aizerman et al., 1964), for the expanded

signal serves as a basis for the vector space of polyno-

mials or at least some ﬁnite dimensional subset of that

vector space. The unit consisting of a polynomial ex-

pansion up to degree two combined with a linear SFA

is usually referred to as SFA(2) or quadratic SFA.

Denoting the original input data or in case of

SFA(2) the expanded data, respectively by

x, param-

eters are learnt by applying SFA to the mean centered

signal x =

x − h

. Obviously x automatically fulﬁlls

constraint 2. Inserting x into the objective function 1

and into equation 4 yields

∆(y

) = h ˙y

= w

=: w

(6)

and

= w

hxx

=: w

. (7)

Furthermore, constraint 3 can be integrated into equa-

tion 1, resulting in the new objective function

∆(y

) =

h ˙y

. (8)

It is known from linear algebra that the solution to

this problem is given by the generalised eigenvalue

approach:

AW = BWL, (9)

letting W = [w

, . . . , w

] be the matrix of the gen-

eralised eigenvectors and L the diagonal matrix of

the corresponding eigenvalues λ

, . . . , λ

. It can be

shown that the orthonormal set of eigenvectors sorted

in descending order accordingly to their correspond-

ing eigenvalues yields the weight vectors w

(Berkes,

2006).

One of the key features of the SFA algorithm is

that if the training signal shares most of the char-

acteristics of the target input signal, the learnt pa-

rameter set will generalise well on unseen data. Al-

though the previously described exact solution of the

optimisation problem is computationally demanding,

the application of a trained SFA(2) to new data sim-

ply consists in the multiplication of the nonlinearly

expanded, mean centered input signal by the SFA

weight matrix W.

Since the input signal might already be from a

high dimensional input space, SFA(2) does, due to the

polynomial expansion, heavily suffer from the curse

of dimensionality. In order to deal with the explosion

in dimensionality SFA can be applied successively

in networks of SFA modules, passing only a limited

amount of slowest components to the next module.

We will reduce the dimensionality of the input by

prepending the SFA(2) module with an SFA(1) mod-

ule.

2.2 Second-order Volterra Filters

It has been shown in (Berkes and Wiskott, 2006) that

every input-output function y

(t) = g

(x) learnt by a

quadratic SFA can be formulated in a general inho-

mogenous quadratic form as given by the following

equation:

(t) = c +f

x +

Hx. (10)

Letting x(t) := [x(t − m + 1), x(t − m + 2), . . . , x(t)],

i.e., a time embedded signal with tap delay m, this

form corresponds to the second-order Volterra series

with ﬁnite kernel, which provides the basis for so-

called Volterra ﬁlters, a type of well-studied nonlin-

ear FIR ﬁlters

(Mathews, 1991; Lau et al., 1992).

The coefﬁcient terms c ∈ R, f ∈ R

and H ∈ R

m×m

are also called the ﬁlter kernels. The relation between

SFA and Volterra ﬁlters is interesting insofar as clas-

sic approaches for the design of these ﬁlters focus on

supervised adaptation, whereas the SFA is a strictly

unsupervised method.

In fact, quadratic ﬁlters are very suitable for the

use with dynamic acceleration sensory data: As de-

scribed in the next section, the robot platform used in

this paper features several pairs of orthogonal acceler-

ation sensors. The two-dimensional vector x formed

by the values of an orthogonal acceleration sensor pair

can be expressed by polar coordinates,

= r cos(φ), x

= r sin(φ), (11)

and obviously, the squared sum of the two sensors

eliminates the sinus and cosinus terms,

+ x

= r

, (12)

thus, being proportional to the energy. As shown be-

low, the described ﬁlter learning algorithms exploit

this fact in order to separate the sensory input signal

into dynamic and static parts, facilitating the smooth-

ing of the signal.

3 EXPERIMENTS

Our experiments were conducted on a humanoid

robot platform which was developed at our laboratory

Finite impulse response ﬁlters.

ICFC 2010 - International Conference on Fuzzy Computation

214

Figure 1: Extract from a high speed video depicting the movement in the coronal plane.

speciﬁcally for researching basic motion capacities,

most importantly biped walking. In this section we

brieﬂy describe our robot platform, the examined gait

pattern and how we use SFA for our aim of increasing

its reactivity.

3.1 Embodiment

The humanoid robots used in our experiment are

robots of the so-called A-series platform. The robot

is based on a commercially available robot kit, called

Bioloid, which was augmented by additional process-

ing power, a camera in the head and several proprio-

ceptive sensors. The robot features 21 degrees of free-

dom, 19 in the body, including elbow, hand, hip, knee

and foot joints, as well as motors driving the pan-and-

tilt unit for the camera. Eight microprocessor boards

are distributed across the body for actuator control,

additionally featuring a two-axes acceleration sensor

each. The boards are located on the hips, arms and

shoulders. Each board controls up to two actuators,

while communicating via a shared system bus, that in-

tegrates incoming and outgoing data from the sensors

and the motors. Throughout our experiments all sen-

sory and motor values were normalised to [−1.0, 1.0].

3.2 Gait Pattern

The studied gait pattern is based on a neurally imple-

mented sensorimotor loop, which was developed at

our laboratory. The underlying neural model consists

of standard time discrete units using the hyperbolic

tangent as a nonlinear transfer function.

The gait pattern starts with an oscillation in the

coronal plane, initiated by letting the robot move its

feet such that it subsequently displaces its weight

from one foot to the other in order to get the feet off

the ground. Figure 1 shows a series of snapshots from

a high speed video depicting this coronal movement.

Then, as soon as a sensory threshold is reached, the

robot starts moving its feet to the front, beginning to

walk.

In this article we concentrate on a speciﬁc piece

of the whole network, namely the part responsible for

the creation of the oscillating movement in the coro-

nal plane. Figure 2 shows the corresponding neu-

ral networks. The blue circles indicate input coming

from the robot’s sensors, red circles output to the mo-

tors and ﬁnally white circles represent the foremen-

tioned neural units. A possible bias value is written

into the neuron. The input values received by the net-

work consist of data from two acceleration sensors

that are located on the robot’s left and right shoulder

and direct to the coronal plane. The calculated out-

put value is passed to the robot’s hip and ankle roll

motors.

In ﬁgure 2(a), the ﬁrst version of the gait net-

work is depicted, which will be called the unﬁltered

gait network. The inputs are fed into a neuron where

they are equally weighted, summed and possibly dis-

torted by the nonlinearity of the hyperbolic tangent.

In this version of the network the output of the neuron

is immediately fed into the motor outputs; however,

conducting the unﬁltered signal directly to the motors

results in high energy consumption and a less stable

movement pattern because of high frequency compo-

nents, which are contained in the possibly noisy ac-

celeration sensor data. Therefore, as shown in ﬁgure

2(b), two IIR ﬁlters

in terms of two leaky integrators

connected in parallel (red neurons and weights) were

introduced into the network serving as a low-pass ﬁl-

ter. We will call this network the IIR gait network.

3.3 Training Data

In order to use the SFA(2) module within the senso-

rimotor loop, the module has to be passively trained

on a recorded walking sequence. For comparison, dif-

ferent sequences were generated and used as training

data: The ﬁrst type of sequences was generated us-

ing the unﬁltered gait network, the second type using

the IIR gait network. The sequences consisted only

of the walking pattern and did mostly not contain any

remarkable disturbances. Sequences were recorded at

100 Hz and were up to 60 seconds long.

In each case the slowest component was used for

the motor outputs. However, the slowest component

had to be multiplied by −0.1 since the sign switched

according to the coronal acceleration sensor, and it

also had to be rescaled in order to be used as a motor

control value.

Inﬁnite impulse response ﬁlters.

USING SLOW FEATURE ANALYSIS TO IMPROVE THE REACTIVITY OF A HUMANOID ROBOT'S

SENSORIMOTOR GAIT PATTERN

215

0.03

-0.03

0.3

0.18

0.3

SLy_fr

SRy_fr

LHipRoll

LAnkleRoll

RHipRoll

RAnkleRoll

0.5

(a) Without Filter.

0.03

-0.03

0.3

0.18

0.3

SLy_fr

SRy_fr

LHipRoll

LAnkleRoll

RHipRoll

RAnkleRoll

0.5

0.08

0.088

-1.1

0.8

0.92

(b) With IIR Filter.

0.03

-0.03

0.3

0.18

0.3

SLy_fr

FLx_fr

LHipRoll

LAnkleRoll

RHipRoll

RAnkleRoll

Expansion

Time

Embedding

SFA

0.1

SLx_sa

Figure 2: Sensorimotor loops generating an oscillation in

the coronal plane. Top: Raw sensorimotor loop without any

ﬁlter. Middle: Intermediate smoothing with an IIR ﬁlter

(red structure). SLy fr and SRy fr denote the robot’s coro-

nal shoulder acceleration sensors. Bottom: Replacing the

IIR ﬁlter by an SFA module. Integrating more sensors into

the SFA module yields more stable output components.

3.4 Application of the SFA

An obvious drawback of using a leaky integrator to

ﬁlter the sensory input is that it decreases the reactiv-

ity of the whole network. Therefore, the ﬁlter structu-

re was replaced by an SFA module as depicted in ﬁg-

ure 2(c). In contrast to the IIR ﬁlter more accelera-

tion sensor values were integrated, namely four sen-

sors from both shoulders and another four sensors lo-

cated at the robot’s feet (overall four sensors directing

to the coronal plane and four to the sagittal plane).

All 16 sensors could have been used, but in order to

keep computational cost low the number of sensors

was reduced as long as no deterioration of the result-

ing SFA(2) components was observed. Interestingly,

the resulting components were slightly better when

also sagittal sensors were fed into the SFA(2) mod-

ule. As previously mentioned, this is owed to the fact

that the orthogonal sensor pairs facilitate the extrac-

tion of dynamic components.

The employed SFA module consists of several

subunits: First, the incoming sensory data is embed-

ded in time. The number of tap delays was set to

m = 8, i.e., the current and the seven prior sensory

data values were passed to the SFA unit, which was

empirically evaluated to be a good compromise be-

tween computational effort and smoothness of the re-

sulting signal. In the next step, the result from the

time embedding is fed into a linear SFA unit which

reduces the dimensionality of the signal to 16 com-

ponents. Then the 16 components are expanded us-

ing a polynomial expansion up to degree 2 and at

last passed to a ﬁnal SFA unit, together forming an

SFA(2) unit. Output signals from both the linear

and the quadratic SFA units are cut off and bound to

[−10.0, 10.0] in order to prevent from very high val-

ues caused by the polynomial expansion. Only the

ﬁrst and thus slowest component y

of the ﬁnal SFA

unit is considered and used as a driving force for the

motor outputs.

Although we described in (Spranger et al., 2009)

that it is possible to obtain very smooth resulting SFA

components by the application of several subsequent

SFA steps and without time embedding, this method

is inappropriate for this task. The reason is that a

cascade of subsequent SFA components adapts very

strongly to the training data, causing heavily jittered

components if applied to even slightly differing un-

seen input data.

4 RESULTS

We conducted several experiments with our robots,

using the SFA implementation available from the

open source Modular Toolkit for Data Processing

(MDP) (Zito et al., 2009).

In order to compare the obtained signals the η

value proposed in (Wiskott and Sejnowski, 2002) was

ICFC 2010 - International Conference on Fuzzy Computation

216

used:

η(y) :=

2π

∆(y), (13)

a smaller value indicating slower signals.

4.1 Extracted SFA Components

Figure 3 plots data stemming from an extract of an

SFA training sequence generated by the unﬁltered gait

network. The acceleration sensor data mix, the sig-

nal obtained by the application of the IIR ﬁlter to the

acceleration data mix and the slowest component ex-

tracted by the SFA module are depicted. All signals

were whitened before plotting for better comparabil-

ity and calculation of η values. The acceleration data

mix’s η value being at 10.45 is much higher than the

values of the IIR and SFA ﬁltered signals ranging both

at about 2.9. It is obvious that the resulting slowest

component is highly correlated to both the accelera-

tion data mix and to the IIR ﬁltered signal. However,

a short delay in the SFA module compared to the other

signals issuing from the time delay is observable. As

shown later this has no negative impact on the reactiv-

ity of the system, although it does slightly lower the

maximum frequency of the coronal oscillation. The

SFA components resulting from training on a IIR gait

network looked similar.

4.2 Comparison to an LMS Adaptive

Volterra Filter

As mentioned before, the trained SFA module corre-

sponds to a second-order Volterra ﬁlter. Therefore,

we compared the SFA module to a ﬁlter obtained

by an adaptive algorithm based on a straightforward

least mean squares (LMS) approach (Lau et al., 1992),

(Zaknich, 2005, chapter 10.4). The algorithm was

trained with the input data and the same tap delay

as the SFA (m = 8), the IIR ﬁlter output was used

as the supervisor signal. The weight terms were ini-

tialised with small random values and different learn-

ing rates µ were tested. Applied to the same acceler-

ation data mix as depicted in ﬁgure 3, the optimal re-

sult of η = 4.36 was achieved with µ = 0.01, yielding

a slightly worse result than the SFA and IIR ﬁlters.

The examination of the weights learnt by the

Volterra ﬁlter as well as the SFA component shows,

that both learning algorithms combine the linear and

the quadratic part in an identical manner: The lin-

ear part contains the main oscillation of the signal,

whilst the quadratic part is irrespective of the oscilla-

tory movement and only captures high-frequent com-

ponents. Hence, by means of the quadratic part high-

frequent and noisy components can be removed from

the signal. Figure 4 shows the slowest SFA compo-

nent and its quadratic and linear parts.

4.3 Using SFA in the Sensorimotor

Loop

As the slowness criterion is not equivalent to the def-

inition of an ideal low-pass ﬁlter, it is by no means

guaranteed that the trained SFA module repels high

frequencies, and therefore there is a risk that high-

frequency components become predominant in the

signal and lead to instability of the whole gait. Any-

way, the SFA module built into the network structure

provided a stable walking gait when trained on walk-

ing sequences generated by the unﬁltered gait net-

work. Unforeseen motor activity with strong jitters

was only experienced if the robot was not upright but

laid down or the like; obviously, this jitters can eas-

ily be avoided, e.g., by using an SFA posture detector

signal inhibiting motor activity in non-upright posi-

tions.

Surprisingly, using an SFA module trained on se-

quences stemming from the IIR gait network yielded a

less stable gait and provoked more jitters. We hypoth-

esise that training an SFA module with noisier input

makes the resulting module more sensitive to the ex-

perienced noise and therefore more stable.

Table 1 summarises the properties of the different

gait networks. For each of the presented networks,

a sequence of 40 seconds was recorded. In order to

obtain the average frequency of the frontal oscillatory

movement of the resulting gait, the autocorrelation of

the equally weighted sum of the two frontal shoul-

der acceleration sensors was calculated. While the

unﬁltered gait network and the IIR ﬁltered gait net-

work produce an oscillation with almost the same fre-

quency, the SFA gait network produces a less dynamic

movement due to the aforementioned tap delay. The

increased amplitude of the unﬁltered gait net results

from instabilities during the training sequence.

Table 1: The average frequency and its amplitude for the

oscillatory movement resulting from the different gait net-

works.

Frequency (Hz) Amplitude

No ﬁlter 0.01475 0.41

IIR 0.01525 0.33

SFA 0.01275 0.32

USING SLOW FEATURE ANALYSIS TO IMPROVE THE REACTIVITY OF A HUMANOID ROBOT'S

SENSORIMOTOR GAIT PATTERN

217

Figure 3: Comparing a weighted sum of the coronal acceleration sensors located at the shoulders to an IIR ﬁltered signal and

the slowest component extracted by SFA.

0 50 100 150 200 250 300

−2

−1

SLy_fr

quadratic part

linear part

Figure 4: The slowest SFA component, separated into its linear and its quadratic part. The linear part contains the oscillatory

movement while the quadratic part consists of noisy

4.4 Impact of Disturbances

Now that we have shown the stability of the modiﬁed

gait network using SFA, we have to give evidence that

the reactivity of the system increases. In order to do

so we consider an artiﬁcially disturbed input signal

and compare the response of the trained SFA mod-

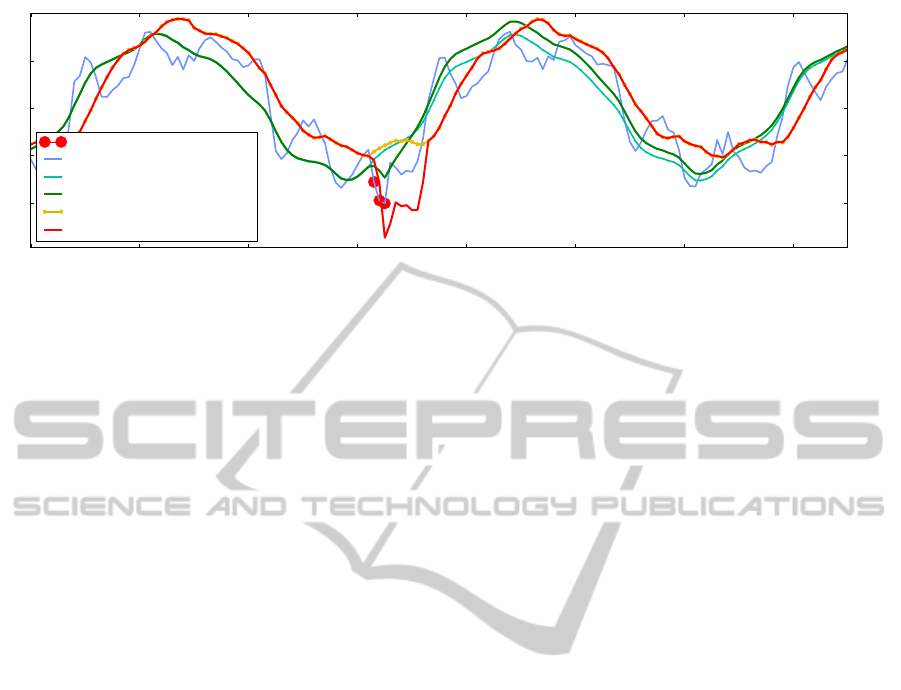
ule to the response of the IIR ﬁlter. Figure 5 shows

both reactions to an artiﬁcial stimulus, consisting of

an increasing negative value of 3 time steps (30 mil-

liseconds) duration added to all coronal sensors. The

dotted lines indicate how the IIR ﬁlter or the SFA

module, respectively, react on the non-disturbed sig-

nal, the continuous lines show the reaction to the dis-

turbance which is indicated by the red dots. While

the IIR ﬁlter remains almost unchanged, the distur-

bance exhibits strong impact on the SFA component

immediately. When disturbing the acceleration sen-

sors with positive values, the SFA component also ex-

hibits a remarkable reaction.

5 CONCLUSIONS AND FUTURE

WORK

We have demonstrated how Slow Feature Analysis, an

unsupervised learning algorithm based on the slow-

ness principle can successfully be integrated into sen-

sorimotor loops for advanced robot control. Using

a time embedded signal of noisy acceleration sensor

data recorded during a walk sequence of a humanoid

robot as training data for the SFA, we get a structure

that is formally equivalent to a second-order Volterra

ﬁlter. The obtained ﬁlter structure extracts the gait

pattern’s main characteristics from the training data

in a reliable and unsupervised manner, reducing noise

and disturbances. More importantly, the ﬁlter can be

used within the sensorimotor loop for the generation

of the walking pattern and its characteristics exhibit

higher reactivity than a comparable IIR ﬁlter.

This insight reveals new perspectives for the op-

portunities to use SFA for signal processing and

within sensorimotor loops, even at low levels which

are directly involved in motor activity control.

Equally, the new structure allows faster detection

ICFC 2010 - International Conference on Fuzzy Computation

218

300 320 340 360 380 400 420 440

−2

−1

IIR vs. SFA: Simulated short-term disturbances

Simulated disturbance

SLx_fr/SRx_fr mix

IIR filter mix

IIR filter mix with disturbance

SFA y

with disturbance

Figure 5: Comparing the response to a short disturbance of the IIR ﬁltered signal and the slowest component extracted by

SFA.

of undesirable conﬁgurations of the robot.

Future work will focus on how the achieved in-

crease in reactivity can be efﬁciently used for the im-

provement of the safety of the gait pattern. Several ap-

proaches are conceivable, e.g., the reduction of motor

activity as soon as the SFA signal leaves its allowed

range. Also one could imagine to use predictors that

are trained on the SFA component; a high prediction

error would then indicate upcoming problems.

Another promising investigation is the online

adaption of the calculated SFA component by an

adaptive LMS algorithm as mentioned in 4.2. This

would prove helpful in cases when the robot’s sensors

are exchanged and therefore slight decalibration may

occur.

In addition, further investigation will be carried

out on the applicability of SFA to other use cases for

humanoid robotics. The newly available successor of

the A-series platform, the Myon robot, is equipped

with a higher amount and additional modalities of

sensors, like pressure sensors located in the feet, etc.

Considering the results hitherto, SFA can prove useful

for the extraction of robust high level abstract features

that meaningfully describe the robot’s states on one

hand, and stabilise robot control on the other hand.

ACKNOWLEDGEMENTS

This work has been supported by the European re-

search project ALEAR (FP7, ICT-214856).

REFERENCES

Aizerman, A., Braverman, E. M., and Rozoner, L. I.

(1964). Theoretical foundations of the potential func-

tion method in pattern recognition learning. Automa-

tion and Remote Control, 25:821–837.

Berkes, P. (2006). Temporal slowness as an unsupervised

learning principle. PhD thesis, Humboldt-Universit

zu Berlin.

Berkes, P. and Wiskott, L. (2002). Applying Slow Feature

Analysis to Image Sequences Yields a Rich Reper-

toire of Complex Cell Properties. In Dorronsoro,

J. R., editor, Proc. Intl. Conf. on Artiﬁcial Neural Net-

works - ICANN’02, Lecture Notes in Computer Sci-

ence, pages 81–86. Springer.

Berkes, P. and Wiskott, L. (2006). On the analysis and inter-

pretation of inhomogeneous quadratic forms as recep-

tive ﬁelds. Neural Computation, 18(8):1868–1895.

Franzius, M., Sprekeler, H., and Wiskott, L. (2007). Slow-

ness and sparseness lead to place, head-direction,

and spatial-view cells. PLoS Computational Biology,

3(8):e166.

Lau, S., Leung, S., and Chan, B. (1992). A reduced rank

second-order adaptive volterra ﬁlter. In ISSPA 92, Sig-

nal Processing and its Applications, pages 561–563,

Gold Coast, Australia.

Mathews, J. (1991). Adaptive polynomial ﬁlters. IEEE Sig-

nal Processing Magazine, 8(3):10–26.

Pfeifer, R. and Bongard, J. C. (2006). How the Body Shapes

the Way We Think: A New View of Intelligence (Brad-

ford Books). The MIT Press.

Spranger, M., H

ofer, S., and Hild, M. (2009). Biologically

inspired posture recognition and posture change de-

tection for humanoid robots. In Proc. IEEE Interna-

tional Conference on Robotics and Biomimetics (RO-

BIO), pages 562–567, Guilin, China.

Wiskott, L. (1998). Learning Invariance Manifolds. In Proc.

of the 5th Joint Symp. on Neural Computation, May

16, San Diego, CA, volume 8, pages 196–203, San

Diego, CA. Univ. of California.

Wiskott, L. (2003). Estimating Driving Forces of Nonsta-

tionary Time Series with Slow Feature Analysis.

Wiskott, L. and Sejnowski, T. (2002). Slow Feature Anal-

ysis: Unsupervised Learning of Invariances. Neural

Computation, 14(4):715–770.

Wyss, R., K

onig, P., and Verschure, P. F. M. J. (2006). A

model of the ventral visual system based on temporal

stability and local memory. PLoS Biol, 4(5).

Zaknich, A. (2005). Principles of adaptive ﬁlters and self-

learning systems. Springer London.

Zito, T., Wilbert, N., Wiskott, L., and Berkes, P. (2009).

Modular toolkit for Data Processing (MDP): a Python

data processing frame work.

USING SLOW FEATURE ANALYSIS TO IMPROVE THE REACTIVITY OF A HUMANOID ROBOT'S

SENSORIMOTOR GAIT PATTERN

219