
OPTIMIZING B-SPLINES USING GENETIC ALGORITHMS
APPLIED TO AIR-TRAFFIC CONFLICT RESOLUTION
Clement Peyronne, Daniel Delahaye
Applied Mathematic Laboratory (LMA), ENAC, 7 rue Edouard Belin, Toulouse, France
Marcel Mongeau
Universite de Toulouse, UPS, INSA, UT1, UTM, Institut de Mathematiques de Toulouse, F-31062 Toulouse, France
CNRS, Institut de Mathematiques de Toulouse UMR 5219, F-31062 Toulouse, France
Laurent Lapasset
Air Traffic Management, Capgemini, Toulouse, France
Keywords:
Air-traffic conflict resolution, B-splines, Genetic algorithms.
Abstract:
Conflict resolution has always been a sensitive matter in air-traffic management. Current European projects
aim partial or total automation of air traffic control to deal with the constant growth of air traffic. Techno-
logical advances on flight management system allows us to consider an automatic conflict resolution using
continuous trajectories. In this paper, we present a new methodology that, first, relies on B-splines to model
trajectories, secondly models air-traffic conflict resolution as an optimization problem whose decision vari-
ables are the spline control points. Finally, we use genetic algorithms to tackle this optimization problem in
order to generate optimal conflict-free situations.
1 INTRODUCTION
From the beginning, the most critical point of air traf-
fic control was to ensure safety separation between
airplanes. To achieve this goal a safety standard sep-
aration distance has been defined: 5 Nm (Nautical
miles) horizontally and 1000 feet vertically. Air traf-
fic controllers are responsible for ensuring the respect
of these separation rules.
1.1 Context
Air traffic being constantly increasing, controllers in
charge of an aviation sector must handle more and
more flights. Up to now, decreasing the size of avi-
ation sectors could compensate the growth of traffic
but we are reaching the point where a decrease of the
size of sectors is no longer efficient.
Nowadays, air traffic management has already
used every available ressource to increase airspace ca-
pacity. However, from now to 2020, air traffic is ex-
pected to be multiplied by two or three. Consequently,
air traffic management (ATM) will have to deal with
this overload while ensuring at least equivalent stan-
dards of safety (Alliot and de Verdi
`
ere, 2003). The
SESAR European project aims at finding solutions
to this problem by providing a decision support to
air traffic controllers in order to decrease their work-
load. Considering the technological advances on the
aircraft flight management system (FMS), we will ex-
plore in this paper the possibility of a full automation
generating continuous trajectories that new FMS can
follow.
1.2 Previous Related Work
By the past, two kinds of method have become pre-
dominant in automatic air traffic conflict resolution
for their good results : genetic algorithms (GA) (Du-
rand, 2004) and navigation functions (Zeghal, 1994).
Genetic algorithms are part of what is known as
natural computation or evolutionary methods. This
optimization method is based on the evolution theory
213
Peyronne C., Delahaye D., Mongeau M. and Lapasset L..
OPTIMIZING B-SPLINES USING GENETIC ALGORITHMS APPLIED TO AIR-TRAFFIC CONFLICT RESOLUTION.
DOI: 10.5220/0003082802130218
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 213-218
ISBN: 978-989-8425-31-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

and uses concepts such as mutation, crossover and,
of course, selection. Each possible solution of our
optimization problem is encoded as a chromosome
via a specific encoding (for example, number and du-
ration of simple maneuvers). The algorithm creates
randomly a first chromosome population. Each chro-
mosome ability to solve the problem (fitness) is then
evaluated. The best individuals (according to their fit-
ness) are selected and mutation, crossover are applied
to obtain a new population of chromosome (next gen-
eration). The user chooses the necessary generation
number for the algorithm to converge (this choice is
usually done empirically).
The obtained trajectories’ velocity stays within ac-
ceptable bounded range with respect to ATM oper-
ational constraints. However, these techniques have
not been tested yet with curved trajectories.
Navigation functions use a different representa-
tion. Indeed, the airspace is considered as a poten-
tial field, and airplanes like particles navigating in it.
Naturally, negative charges represent obstacles to the
airplane (other aircrafts, congested areas) and positive
charges, its destination. As a result, each airplane is
attracted to its destination while being repulsed by ob-
stacles which enables to the automatic generation of
conflict-free trajectories.
Figure 1: Principle of navigation functions between two air-
crafts (left), between an aircraft and an obstacle (right).
It has been demonstrated that navigation function
methods ensure collision avoidance and connection
between departure and destination. The major draw-
back of this method is that the obtained solution does
not respect the ATM constraints such as limited speed,
or trajectory smoothness. Evenmore, they can lead to
major delays and overcosts as they tolerate any devi-
ation from the business trajectories (BT : the straight
line between the departure and arrival points).
In this paper, we present a new methodology that,
first, relies on B-splines to model trajectories, sec-
ondly models air-traffic conflict resolution as an op-
timization problem whose decision variables are the
spline control points. Finally, we use genetic algo-
rithms to tackle this optimization problem in order to
generate optimal conflict-free situations.
We present our trajectory model in Section 2. Sec-
tion 3 presents the optimization method we chose to
solve our optimization problem: genetic algorithms
(GA). We detail in Section 4 the objective function
(conflict detection) of our optimization problem. Nu-
merical results are presented in Section 5. We draw
conclusions in Section 6.
2 TRAJECTORY MODEL
B-spline was primarily introduced to find a curve in-
terpolating a set of points of R
2
called control points.
It was later extended to approximation, thereby avoid-
ing the undesirable oscillation inherent to interpola-
tion. In our study, we shall focus on this use of splines
to approximate a set of control points. The control
polygon, the piecewise linear curve linking the control
points, completely defines the curve (Rabut, 2008).
Basically, B-splines are parameterized curves gen-
eralizing the Bezier curve concept. It is an efficient
approximation tool which is constructed from poly-
nomial pieces joined at certain parameter’s values
called knots, stored in a knot vector. In a very sim-
plified way, if we consider a set of control points
(X
i
,Y
i
) = P
i
∈ R
2
(i = 0, 1, ..., n), and a parameter u,
we can define the B-spline as follows :
C(u) = (σ
x
(u), σ
y
(u)), u ∈ [a, b]
where σ
x
(u) and σ
y
(u) are the B-splines approxi-
mations of the couples (i, X
i
)
i=0:n
and (i,Y
i
)
i=0:n
for
u ∈ [a, b] .
Theoritically, the curve is calculated by multiply-
ing the B-splines basis functions by the control points
coordinates. For σ
x
:
σ
x
(u) =
n+1
∑
i=−1
X
i
B
i
(u) (1)
However, in practice, B
i
construction is made by
recurrence. Consequently, we used a more numeri-
cally convenient way to calculate the B-spline values
only using control points values. The B-spline and its
derivative values at knot u
i
are defined by :
σ
i
=
X
i+1
+4X
i
+X
i−1
6
σ
0
i
=
X
i+1
−X
i−1
2h
σ
00
i
=
X
i+1
−2X
i
+X
i−1
h
2
σ
000
i
=
X
i+2
−3X
i+1
+3X
i
−X
i−1
h
3
(2)
ICEC 2010 - International Conference on Evolutionary Computation
214

Therefore, by using Taylor series, we obtain the B-
spline value for all u ∈ [u
i
,
i+1
]:
σ
x
(u) = σ
x
i
+ (u − u
i
)(σ
0
x
i
+ (u − u
i
)(
σ
00
x
i
2
+ (u − u
i
)
σ
000
x
i
6
))
(3)
We choose to rely on B-spline modeling trajectories
because it is a very efficient tool for curve approx-
imation in terms of both approximation quality and
computational time. Moreover, B-splines feature in-
teresting properties such as C
2
-continuity (crucial for
modeling smooth aircraft trajectories), robustness and
flexibility (if one control point is displaced, only a
small part of the curve will be affected). The last
good point in favor of B-splines is its compatibility
with GA : the curve is completely determined by few
control points only, which will be the optimization pa-
rameters of the GA. In our study, we use a fixed max-
imal number of control points between the departure
and the arrival points.
3 OPTIMIZATION METHOD
When several aircraft are involved in a conflict, the
conflict resolution problem has been shown to be NP-
hard (Durand, 2004). Moreover, the optimization
variables being the B-splines control-point location,
we shall see that our objective function (4) is not
differentiable with respect to these variables. Con-
sequently, we must rely on black box (direct) opti-
mization methods to address our problem. In this pa-
per, we choose to use a stochastic global optimization
method, genetic algorithms, to guide the control-point
location. As we mentioned in the previous part, GA
seem to be appropriate with B-splines. In this section,
we explain briefly GA theory and then we shall detail
how we adapt the different operators (selection, muta-
tion and crossover) to our air traffic conflict resolution
problem.
3.1 Basis of Genetic Algorithms
Evolutionary algorithms use techniques inspired by
evolutionary biology such as inheritance, mutation,
natural selection, and recombination (or crossover) to
find approximate solutions to optimization problems
(Goldberg, 1989), (Koza, 1992). An individual, or so-
lution to the problem to be solved, is represented by
a list of parameters, called chromosome or genome.
Initially several such individuals are randomly gener-
ated to form the first initial population (POP(k) with
k = 0 on Figure 2). Then each individual is evaluated,
and a value of fitness is returned by a fitness function
Figure 2: Genetic algorithm with tournament selection. The
first step consists in the selection of the best individuals
from population POP(k). Afterwards, recombination op-
erators are applied in order to produce the POP(k + 1) pop-
ulation.
(generally, the objective function of our optimization
problem). This initial population undergoes a selec-
tion process which identifies the most adapted indi-
viduals. The selection process which has been used in
our experiments is a deterministic (λ, µ)-tournament
selection. This selection begins by randomly select-
ing λ individuals from the current population POP(k)
and keeps the µ bests (λ > µ). These two steps are re-
peated until a new intermediate population (POP
i
) is
completed. Following selection, one of the three fol-
lowing operators is applied : nothing, crossover, and
mutation. The associated probability of application
are respectively (1− p
c
− p
m
)), p
c
and p
m
. Crossover
results in two new child chromosomes, which are
added to the next generation population. The chro-
mosomes of the parents are mixed during crossover.
These processes ultimately result in the next gener-
ation population of chromosomes (POP(k+1) on Fig-
ure 2) that is different from the initial generation. This
generational process is repeated until a termination
condition has been reached. The next section presents
the application of this algorithm to our specific prob-
lem.
3.2 Chromosome Encoding and Fitness
Calculus
In this section we detail the link between our model-
ing method and genetic algorithms. Indeed, our op-
timization method is using B-splines to calculate the
aircraft trajectories in order to determine each individ-
uals fitness. To define this interaction, we first define
an encoding.
A chromosome will represent the trajectories of
N aircrafts using a matrix of N × N
c
where N
c
is the
maximal number of control points we wish to con-
OPTIMIZING B-SPLINES USING GENETIC ALGORITHMS APPLIED TO AIR-TRAFFIC CONFLICT RESOLUTION
215
sider. For example, the case where N = 20 airplanes
and N
c
= 2 we encode the trajectories as follows :
Airplane1 P
1
1
P
1
2
Airplane2 P
2
1
P
2
2
... ... ...
Airplane19 P
19
1
P
19
2
Airplane20 P
20
1
P
20
2
Obviously, departure and arrival points are not en-
coded in the chromosome as they are not meant to
move, they are not optimization variable.
Let us now define precisely how we specify the
control points P
j
i
. We want a compromise between
allowing the trajectory to deviate freely (in any direc-
tions) from the business trajectory (BT) and staying
as close as possible from it. For that purpose, we de-
fine a fixed width band (D
max
), depending on the BT
length (D
tot
), around the BT trajectory where the con-
trol points are allowed to lie.
A matter for the control point location is that, if
there are all gathered in the same region, it can create
oscillations on the resultant trajectory. Consequently,
we distribute uniformly the control points along the
BT.
To summarize, a control point can be defined by
a single parameter representing a bandwidth percent-
age (±
d
D
max
% ).
Moreover, it is desirable to be able to have
a different number of control points for a given
chromosome. In order to satisfy this goal, we
used a convention: percentage are generated within
[−200%;200%], if the percentage is between −100%
and 100%, then we create a control point, if it belongs
to [−200%;−100%[∪[100%;200%], we do not. Con-
sequently, our chromosome is a N × N
c
matrix of per-
centage. Several cases are presented in Figure 3 and
4.
Figure 3: Chromosome encoding and corresponding B-
spline with one percentage exceeding 100%.
3.3 Crossover and Mutation
Let us now describe how we adapted the genetic op-
erators we use in our GA.
Figure 4: Another chromosome encoding and its
corresponding B-spline with both percentages within
[−100%, −100%].
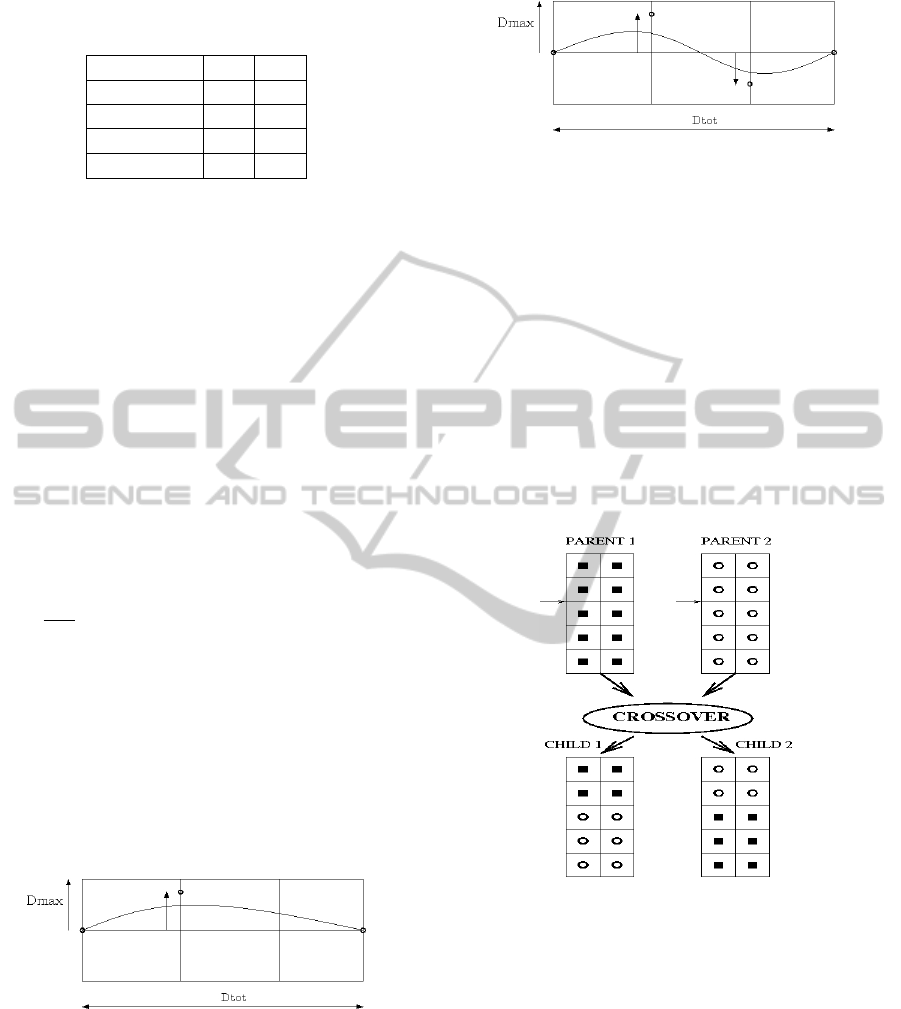
3.3.1 Slicing Crossover
The crossover operator aims at finding better solu-
tions by mixing two good individuals of the previ-
ous generation. Therefore, we decide to keep trajec-
tory consistencies by inverting only complete trajec-
tories using a slicing crossover (we do not separate
control points belonging to the same trajectory). Ac-
cordingly, the crossover consists in picking a plane
number randomly and inverting the parent trajecto-
ries corresponding to the next aircrafts. An example
is given in Figure 5 :
Figure 5: Parent and children chromosomes.
3.3.2 Mutation
The mutation operator aims at diversifying the genes
in the population in order to explore as much as
possible the problem space. Thus, mutation con-
sists in choosing randomly one control point in the
chromosome and to assign to it a new random num-
ber (using a uniform distribution) in the interval
[−200%;200%]. (see Figure 6).
ICEC 2010 - International Conference on Evolutionary Computation
216

Figure 6: Initial and mutated chromosome.
4 OBJECTIVE FUNCTION :
CONFLICT DETECTION
METHOD
In order to evaluate each chromosome fitness, we de-
code it into N trajectory curves (one per aircraft) and
evaluate two quantities. First, how many conflicts the
situation engenders and secondly what is the total ex-
tra distance induced with respect to the BT. To cal-
culate these quantities, we discretize the airspace into
square cells of size half the standard separation (noted
d). Our conflict detection is performed in two steps :
• First, for each airplane, we store the grid’s cells
through which the aircraft flies, the aircraft num-
ber (its label), the entry and exit times in and out
each of the stored cell,
• Then, we select each stored cell and we check
whether any other airplane goes through any of
the eight neighboring cells for other airplanes. If
there are such airplanes, we check the time to see
whether there is a conflict between these two air-
planes. If so, we calculate the conflict duration.
Our conflict detection procedure send back the
chromosome fitness to the GA. Here is the formula
we use to calculate the fitness:
f (X ) = −(CN + (
N
∑
i=1
NR
i
BT
i
− N)) (4)
where CN is the number of conflict, NR
i
the length
of the new route calculated by the algorithm for the
aircraft i, while BT
i
the length of the business tra-
jectory (straight line from the departure to the arrival
point) and N the number of aircraft. High fitness cor-
responds to good individuals. Indeed, the lower are
the number of conflict and the route lengthening, the
better is the chromosome.
5 RESULTS AND PERSPECTIVES
In this section, we present several results we obtained
using our methodology. First, we test our method on
the roundabout test problem which is a very common
test on automatic conflict-detection method. It con-
sists in making a certain number of planes fly to the
diametrically opposed point at a common speed (each
point on the circle has an outgoing and an incoming
trajectory).
We choose to fly N = 16 aircrafts for results’
readability) equidistributed on a circle of 100Nm(=
185200m) radius To address this conflict resolution,
we use the following parameters :
• Number of generation : 100.
• Size of the population : 500.
• Mutation probability : p
m
= 0.3.
• Crossover probability : p
c
= 0.6.
• Maximal number of control points : N
c
= 2.
To compute the conflict resolution, we used a
2.53GHz Intel(R) Core(TM)2 Duo on a Windows
Vista Operating System and we coded in Java. The
obtained conflict-free situation is presented in meter-
scale (1Nm = 1852m) in Figure 7. This whole resolu-
tion computation required approximately 4 minutes.
Figure 7: The roundabout configuration after resolution.
The fitness’ evolution with respect to generations
is shown in Figure 8. The fitness is meant to increase
to 0 as formula (4) shows. Moreover, when the fit-
ness is in [−1, 0] the situation is conflict-free. Conse-
quently, the algorithm stops only when the best indi-
vidual fitness is in [−1, 0].
Although one can easily solve intuitively this aca-
demic problem due to its symmetry, our automatic
implementation does not exploit any symmetry here.
This result shows that our methodology is promising
as the obtained conflict resolution is consistent with
experts’ experience.
We also test our methodology on a more realistic
operational problem where N = 15 aircrafts are in-
volved in a fuzzy convergence. In this situation, for
OPTIMIZING B-SPLINES USING GENETIC ALGORITHMS APPLIED TO AIR-TRAFFIC CONFLICT RESOLUTION
217

Figure 8: The fitness evolution with respect the generation.
each aircraft, we have its departure point, its head-
ing and its speed. To calculate the arrival points, we
make the 15 aircrafts fly for one hour at a constant
speed, on a straight line following the initial direction
(heading). We present the conflict-free situations our
algorithm obtains is displayed in Figure 9.
Figure 9: The operational problem after resolution.
We can see on Figure 10 that on an operational
application, our method converges far more rapidly in
three generations (90 generations for the roundabout
test problem). This results shows that our method can
be very efficient from an operational point of view.
Indeed, in operational problems, there are never more
than four aircrafts involved in the same conflict. Con-
sequently, our algorithm will be able to deal very effi-
ciently with operational air traffic. For this situation,
we used a different number of generations because of
its extremely quick convergence (number of genera-
tion: 20). Moreover, we can see that few aircrafts
are deviated, which is consistent with a controller be-
haviour, who would prefer to deviate largely one air-
craft instead of deviating lightly several aircrafts to
solve conflicts.
6 CONCLUSIONS
We have shown in this paper that the combination of
B-splines and genetic algorithms can be a promising
methodology for automatic conflict resolution in air
traffic control. However, we have in mind several
Figure 10: The fitness evolution with respect the generation.
developments to improve our approach such as us-
ing sharing in GA (deals with equirepartition of the
population on the different maximums) in our GA
or implementing a self-adaptative GA (every param-
eter such as bandwidth, control points’ number, etc
will be considered within the chromosome encoding,
as proper optimization variables). Furthermore, we
plan to exploit our B-spline model of trajectory to ad-
dress the conflict resolution problem with determinis-
tic derivative-free optimization methods (Conn et al.,
2009). Indeed, despite the local aspect of these meth-
ods, they can also be adapted to global optimization.
ACKNOWLEDGEMENTS
This work has been supported by French National Re-
search Agency (ANR) through COSINUS program
(project ID4CS n°ANR-09-COSI-005) and Capgem-
ini through the first author PhD funding.
REFERENCES
Alliot, J. and de Verdi
`
ere, D. C. (2003). L’ATM : 20 ans
d’efforts et perspectives. In Vers l’automatisation du
vol et de sa gestion.
Conn, A., Scheinberg, K., and Vicente, L. (2009). Introduc-
tion to derivative-free optimization. Society for Indus-
trial and Applied Mathematics.
Durand, N. (2004). Algorithmes g
´
en
´
etiques et autres outils
d’optimisation appliqu
´
es
`
a la gestion du trafic a
´
erien.
PhD thesis, CENA, Toulouse.
Goldberg, D. (1989). Genetic Algorithms in Search Opti-
mization and Machine Learning. Reading MA Addi-
son Wesley.
Koza, J. (1992). Genetic Programming. MIT press.
Rabut, C. (2008). Courbes, outils pour la CAO, approxima-
tion
`
a une variable. INSA-Toulouse lecture notes.
Zeghal, K. (1994). Vers une th
´
eorie de la coordination
d’actions, application
`
a la navigation a
´
erienne. PhD
thesis, Universit
´
e Paris VI.
ICEC 2010 - International Conference on Evolutionary Computation
218
