NANOSTRUCTURES THERMAL EMISSION OPTIMIZATION
USING GENETIC ALGORITHMS AND PARTICLE SWARMS
E. Nefzaoui, J. Drevillon and K. Joulain
Institut Pprime, CNRS-Universit
´
e de Poitiers-ENSMA, D
´
epartement Fluides, Thermique, Combustion
ESIP-B
ˆ
atiment de m
´
ecanique, 40, avenue du Recteur Pineau, F 86022 Poitiers, Cedex, France
Keywords:
Particle swarm, Genetic algorithm, Optimization, Coherent thermal emission, Nanostructure.
Abstract:
Nanotechnologies and nanofabrication techniques provided unmeasureable possibilities to control intrinsic
microscopic features of materials and structures in the last years. In particular, materials optical properties and
light propagation control have been some of the most challenging problems due to their various application
possiblities. The present investigation shows that temporally coherent thermal sources have been success-
fully designed and optimized with evolutionary optimization methods such as genetic algorithms and particle
swarms. This lead to a bilayer structure of germanium and silicon carbide, which is, to our knowledge, the
simplest existing structure with such properties.
1 INTRODUCTION
Thermal sources radiative emission has been for a
long time thought to follow the black body laws. This
implies emission in quasi all space directions and
over a wide wavelengths range. Recently, thanks to
advances in materials nanostructuration and related
theoretical developments, this paradigm could be
surpassed (Greffet and Carminati, 1999; Shchegrov
et al., 2000), and sources that exhibit a temporal
(temporal coherence is used for monochromatic emis-
sion or emission in a very narrow spectral domain)
and/or spatial (spatial coherence means emission in
specific directions) coherent emission have been de-
signed and fabricated (Sai et al., 2001; Greffet et al.,
2002; Richter et al., 1993). This kind of sources are
of great interest for new energy conversion devices
which aim to improve energy converters such as ther-
mophotovoltaic devices, for radiation detectors and
radiative cooling systems. These sources could be re-
alized with various structures exploiting completely
different physical phenomena. First, sources of coher-
ent spontaneous emission such as polar materials sur-
mounted by an appropriate surface grating (exploit-
ing surface phonon-polaritons diffraction in the far
field) (Greffet et al., 2002) or those based on left-
handed materials (artificial materials with a refrac-
tive index much lower than 1) (Enoch et al., 2002)
emitted essentially in the visible spectrum which is
not the wavelength range concerned by thermal emis-
sion at usual temperatures (room temperature for
example). Later, photonic crystals (PC) (periodic
dielectric/metallo-dielectric nanostructures that allow
the photons propagation control) made possible the
design of infrared (IR) temporally coherent thermal
emitters, when introducing a defect in the periodicity
of a PC for example (Ben-Abdallah and Ni, 2005).
As for spatial coherence, it was obtained with var-
ious structures like resonant cavities coupled with
metallic layers (Celanovic et al., 2005), surface grat-
ings coupled with waveguides (Joulain and Loizeau,
2007) or a polar material coupled with a semi-infinite
PC (Lee et al., 2005; Fu et al., 2005). A general
method for spatially and temporally coherent IR ther-
mal sources ab-initio design, based on genetic algo-
rithms, was proposed for the first time by Drevillon
(Drevillon and Ben-Abdallah, 2007). This method
leads to interesting multilayer structures which could
not be found easily by a rational reasoning because
of their complexity and random internal structure. In
spite of their academic importance, their complexity
makes their fabrication at a large scale as difficult as
other previously proposed structures such as PC. They
though led, after some optimization effort, using par-
ticle swarm optimization, to very simple structures,
bilayer structures in this case, which exhibit very high
temporal coherence properties. Theses structures are
very interesting since they provide very suitable solu-
tions for industrialization. Besides, their simple inter-
nal composition allows an easier analytical approach
to understand the underlying physical phenomena of
such particular coherence properties.
219
Nefzaoui E., Drevillon J. and Joulain K..
NANOSTRUCTURES THERMAL EMISSION OPTIMIZATION USING GENETIC ALGORITHMS AND PARTICLE SWARMS.
DOI: 10.5220/0003083802190224
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 219-224
ISBN: 978-989-8425-31-7
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

2 MULTILAYER STRUCTURES
AND GENETIC ALGORITHM
OPTIMIZATION
In this section, a brief presentation of multilayer struc-
tures and methods used to calculate their radiative
properties is proposed. Their optimization approach
with a genetic algorithm is then introduced as well as
some of the remarkable obtained results.
2.1 Multilayer Structures
An example of structures considered in this work is
presented in Figure 1. Each structure is composed of
N layers of the same thickness L. Two kinds of struc-
tures have been investigated: those with metals and
polar materials. Each structure contains at least an
absorbent (Silver (Ag), and Silicon carbide (SiC) are
used here) and a transparent material (Silicon diox-
ide (SiO
2
),Silicon (Si) and Germanium (Ge)) in the
considered wavelength range. We are interested in
the radiative properties of these structures thus in the
spectral and directional emissivity ε(λ, θ), reflectiv-
ity r(λ, θ) and transmittivity t(λ, θ). These quantities
are calculated with the basic electromagnetism rela-
tions and the whole structure properties obtained with
the transfer matrix formalism as detailed by Drevil-
lon (Drevillon, 2007). Simplest obtained structures
are compound of 50 layers 50-nanometer thick each.
If three different materials are considered in such a
structure, more than 7 × 10
23
different structures are
possible. A stochastic method such as genetic algo-
rithms (GA) to explore the search domain is then very
useful.
2.2 Genetic Algorithm
Since we were looking for a structure with certain
emissivity and reflectivity, the following objective
function (fitness) had to be minimized:
J =
∑
p
Z
θ
2
θ
1
Z
λ
max
λ
min

ε
target
(λ, θ) − ε
p
struc
(λ, θ)

2
dθdλ
+
∑
p
Z
θ
2
θ
1
Z
λ
max
λ
min

r
target
(λ, θ) − r
p
struc
(λ, θ)

2
dθdλ
(1)
where the discrete sum operates over both thermal
radiation polarization states. ε
target
and r
target
are the
desired emissivity and reflectivity and ε and r those
of the optimized structure. A simplified version of ge-
netic algorithm was first developed. Considered struc-
tures were always made of the same number of lay-
ers, and all layers had the same thickness. The only
Figure 1: Schematic of the planar structure made of N lay-
ers of linear dielectrics coated on a semi-infinite substrate.
The electric field in out EL = (EL
in
, EL
out
) on the left-hand
side of the structure is linearly related to the electric field
ER = (ER
out
, ER
in
) on the right-hand side (Here, only the
scattering of TE waves is illustrated. k is the wave vector of
the incident field).
variable parameter to optimize was the different lay-
ers order. For instance, if we are in the presence of a
two materials structure (material 0 and material 1), it
can be represented by a binary sequence of the form
01001101110 . . . . A random population is initially
generated and the objective function of each individ-
ual is then calculated. A pair number of structures
among those with the lowest fitness is selected and a
crossover is performed between each structures pair.
The crossover operation consisted in partially mixing
the binary sequences of a pair of structures. For ex-
ample, the structures 110010011 and 01011001 are
split and recombined to form two children structures
110011001 and 01010011. The new generation in-
dividuals fitness is calculated and the same operation
repeated until obtaining a satisfactory fitness. A mu-
tation operator was necessary to avoid convergence
to local minima. Some of the obtained results are
presented in the following paragraph. A schematic
diagram of this algorithm is presented in Figure 2.
An initial population of 100 individuals was usually
adopted and the stopping criteria was a sufficiently
small fitness or a maximal number of iterations (be-
tween 100 and 200). Nevertheless, the best struc-
tures’ fitness varied highly and the algorithm always
stopped when reaching the maximal iterations num-
ber. A variable mutation probability p
m
was used and
updated at each iteration as detailed in (Drevillon and
Ben-Abdallah, 2007)
ICEC 2010 - International Conference on Evolutionary Computation
220

Figure 2: Principle of genetic algorithm GA used to design a
binary nanostructured one-dimensional functional material.
Here, the main steps of GA are described: initialization of
a random population, selection of parents generation, cross
over, and mutation.
2.3 Results
First, a temporally coherent thermal source in the
wavelength range [8, 14]µm using 50 layers of three
materials was looked for. In this wavelength domain,
Germanium (Ge) and Cadmium Telluride (CdTe)
are transparent with approximate dielectric constants
ε
Ge
= 16 and ε
CdTe
= 7.29 respectively (Palik, 1998).
Silicon Carbide (SiC) is the absorbent material. Its
dielectric permittivity is well described by the oscil-
lating Lorentz’s model (Palik, 1998)
ε
SiC
= ε
∞

1 +
ω
2
L
− ω
2
T
ω
2
T
− ω
2
− ıΓω

(2)
where ω
L
= 18.253 × 10
13
rad.s
−1
, ω
T
= 14.937 ×
10
13
rad.s
−1
, Γ = 8.966 × 10
11
rad.s
−1
and ε
∞
= 6.7
are the longitudinal and transverse optical phonon
pulsations, the damping factor and the high frequency
dielectric constant respectively. A very satisfying
structure obtained by this mean is presented in Fig-
ure 3. Its directional and spectral emissivity for the
TE polarization as well as target emissivity are pre-
sented in Figure 4. The obtained source emissivity
exhibits a very narrow peak around the wavelength
λ
m
= 12.6µm that culminates at ε
max
= 0.9 for both
polarizations. However, a degradation of the emission
coherence occurs at large angles for TM polarization.
The obtained source radiative properties are very in-
teresting, since they present the highest coherence de-
grees ever observed with thermal sources at this wave-
length range. However, its structure is still quite com-
Figure 3: A schematic of a multilayer structure of Ge, SiC
and CdTe made of 50 50-nanometer thick layers and ob-
tained by a genetic algorithm in order to have a coherent
emission around λ = 12.6µm.
Figure 4: Spectral and directional emissivity (TE polariza-
tion) of the multilayer structure presented in Figure 3 and
target emissivity adopted in the optimization process by the
GA.
plex from an industrial point of view and still needs
further improvements. In the following section, an-
other optimization method is adopted, and we show
that it allowed the design of structures as simple as a
bilayer and with coherence degrees even higher than
those of the structure aforementioned.
NANOSTRUCTURES THERMAL EMISSION OPTIMIZATION USING GENETIC ALGORITHMS AND PARTICLE
SWARMS
221

3 BILAYER STRUCTURES
AND PARTICLE SWARMS
OPTIMIZATION (PSO)
Starting from the structures obtained with GA and
with a manual trial and error approach, it has been
shown that simpler structures with a high coherence
degree were realizable. A PSO algorithm was used
to optimize them taking into account more param-
eters like dielectric permittivities and layers thick-
nesses which allowed to understand their influence on
such radiative properties and the underlying physical
phenomena. Finally, the design of other IR coher-
ent thermal sources with different materials and over
other wavelength domains was made possible. These
different steps and obtained results are presented in
the following paragraphs.
3.1 Trial and Error Approach
Even if the structure presented in Figure 3 is made
of 50 elementary layers, it is obvious that this number
can be reduced thanks to the existence of adjacent lay-
ers of the same materials. According to Figure 3 it can
be reduced to at least 13, without changing the global
structure. After more than 35 trials and errors, where
layers thicknesses, the number of layers, and their or-
ganization were modified manually, a simpler coher-
ent source could be obtained by eliminating CdTe and
using only Ge and SiC. This structure is presented
in Figure 5 and its directional and spectral emissivity
and reflectivity are plotted in Figure 6. It is clear that
Figure 5: Bilayer structure made of a 700nm thick Ge layer
and a 200nm thick SiC layer. This structure was obtained
when trying to simplify manually the 50 layers structure
obtained by GA while keeping high coherence and emis-
sion properties.
coherence properties, compared to those of the multi-
layer structure of Figure 3 are improved. The trial and
error process does not allow to find the optimal struc-
ture since many local minima exist around the global
minimum. Founding the global minimum this way
Figure 6: Spectral and directional emissivity for TM (a) ,
TE (b) polarizations, and reflectivity for TM (c) , TE (d) po-
larizations of the quasimonochromatic thermal source pre-
sented in Figure 5.
would at least necessitate a big number of off-putting
essays. We also wanted to know whether it was pos-
sible to obtain coherent sources with other materials.
A PSO algorithm was then used.
3.2 PSO and Bilayer Optimization
To determine the optimal bilayer structure with SiC
and Ge or any other transparent material and in order
to know whether other coherent emitting structures
with different materials were possible, we had to ex-
plore a search space with more dimensions. We then
adopted PSO and looked for the optimal layers thick-
nesses and materials dielectric permittivities. We al-
though kept the same form of the absorbent material
dielectric permittivity (Lorentz oscillator). Particles
were initialized with random positions (x
i
) and nil ve-
locities (v
i
). Then, they were updated at each iteration
as following:
v
i
= ωv
i
+ c
1
r
1
(x
bn,i
− x
i
) + c
2
r
2
(x
bm,i
− x
i
)(3)
x
i
= x
i
+ v
i
(4)
where ω = 0.729 is inertia weight factor, r
1
and r
2
are two random factors, c
1
= 1.494 and c
2
= 1.494
are the ”social” and ”cognitive” weight factors, x
bn,i
and x
bm,i
the best positions in the particle i neighbor-
hood and memory respectively. Populations were al-
ways composed of 20 particles. 1000 iterations were
sufficient to obtain the best structures. Finally, since
physical parameters are looked for, all values are not
allowed for the optimized parameters. When a parti-
cle run out of the search domain, it was put back on its
boundary with a nil velocity. This procedure showed
that for SiC and Ge structures, the optimum is ob-
tained for slightly different thicknesses (d
Sic
= 65nm
and d
Ge
= 735nm) and that it is possible to design
ICEC 2010 - International Conference on Evolutionary Computation
222

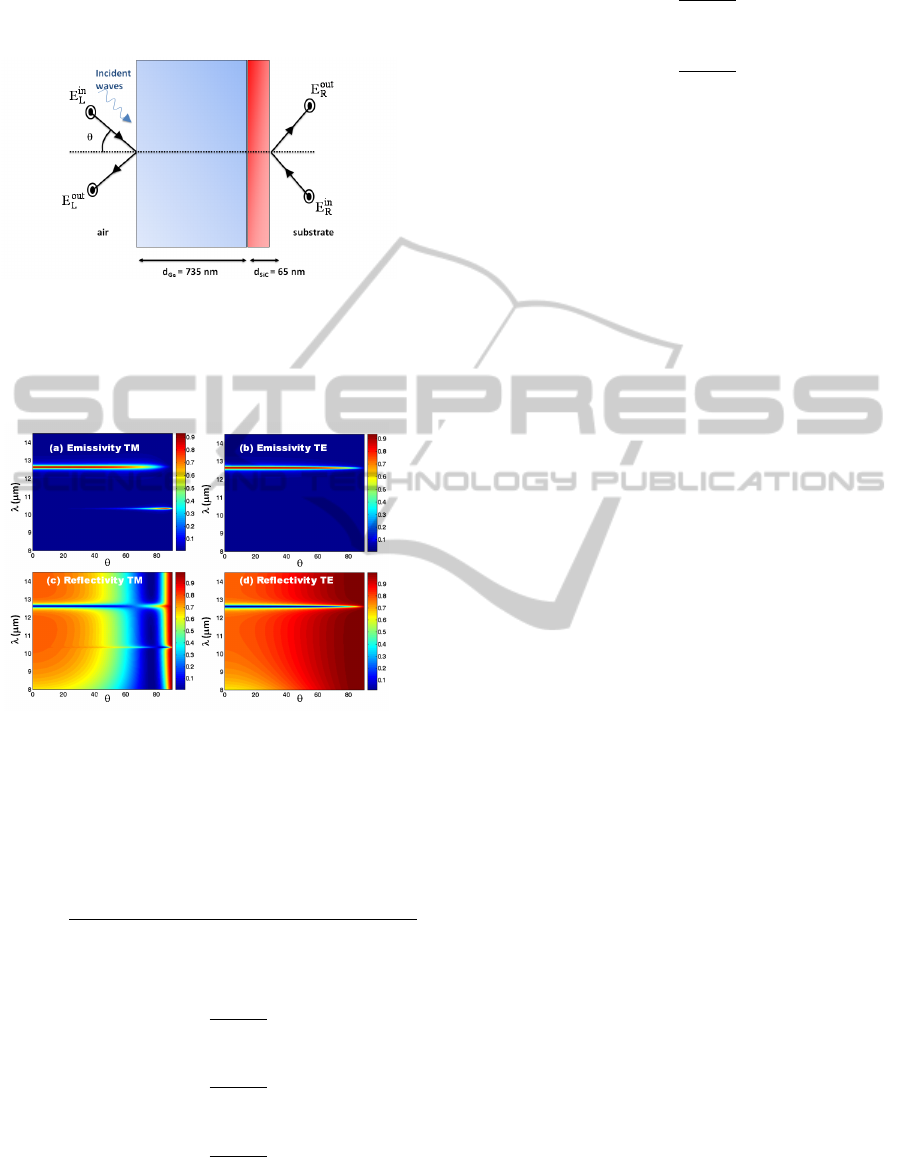
coherent thermal sources with other materials. The
resulting Ge − SiC structure is presented in Figure 7
and its radiative properties in Figure 8. Thanks to
Figure 7: Optimal quasimonochromatic structure made of
a 735nm thick Ge layer and a 65nm thick SiC layer. This
structure was obtained when trying to improve the previ-
ously and manually obtained bilayer structure (Figure 5)
using PSO. This structure presents the highest emission in-
tensity while conserving the best coherence level.
Figure 8: Spectral and directional emissivity for TM (a), TE
(b) polarization, and reflectivity for TM (c), TE (d) polar-
ization of the optimal quasimonochromatic thermal source
obtained by PSO and presented in Figure 7.
the simplicity of bilayer structures, an analytical ap-
proach is possible. The reflectivity of such a structure
is given by:
re
ıδ
=
r
12
+ r
23
e
−ı∆
2
+ r
34
e
−ı(∆
2
+∆
3
)
+ r
12
r
23
r
34
e
−i∆
3
1 + r
12
r
23
e
−ı∆
2
+ r
12
r
34
e
−ı(∆
2
+∆
3
)
+ r
23
r
34
e
−i∆
3
(5)
where
r
12
=
n
1
− n
2
n
1
+ n
2
(6)
r
23
=
n
2
− ˜n
3
n
2
+ ˜n
3
(7)
r
34
=
˜n
3
− n
4
˜n
3
+ n
4
(8)
are Fresnel reflexion coefficients between media 1-2,
2-3 and 3-4 respectively and
∆
2
=
4πd
2
n
2
λ
(9)
∆
3
=
4πd
3
˜n
3
λ
(10)
are the electromagnetic wave phase shifts due to the
propagation through media 2 and 3 respectively. d
2
and d
3
are the thicknesses of the layers 2 and 3 , n
1
,
n
2
, ˜n
3
and n
4
are the refractive indices of the media
1 (air), 2(Ge) , 3(SiC) and 4(air). The tilde on ˜n
3
means that this quantity is complex since SiC is an ab-
sorbent medium in the considered wavelength range.
We realized that for thicknesses given by PSO, the
structure reflectivity goes to zero at the emission peak
wavelength and is very high for other wavelengths.
This means that Ge layer plays the role of an antire-
flector for a certain wavelength. This is possible be-
cause Ge layer thickness, Ge and SiC dielectric per-
mittivities satisfy particular conditions(Zhang, 2007).
Besides, SiC dielectric permittivity resonance occurs
at this same wavelength. SiC layer is then excited at
its resonance which leads to the high emissivity. For
other wavelengths incident radiation is reflected and
can not reach SiC layer. In addition, the highest coher-
ence degree and emission intensity are obtained only
for d
SiC
= 65nm. In fact, SiC layer also plays a waveg-
uide role. For higher thicknesses, more modes around
the resonance mode can propagate which leads to a
coherence loss. For lower thicknesses, the structure
is not opaque anymore since the absorbent layer is
then thinner than the penetration depth. An increase
of transmittivity leads to a loss in the emissivity in-
tensity . Taking into account these different obser-
vations which have been made possible by the sim-
plicity and accuracy of PSO results, other coherent
thermal sources could be designed. For instance, a bi-
layer structure constituted of a 450nm thick Ge layer
and a 310nm thick boron nitride (BN) layer presents
original coherence properties around λ = 9.3µm. BN
dielectric permittivity is modeled by a Lorentz oscil-
lator (Palik, 1998). This structure emissivity for TM
polarization is given in Figure 9.
Due to the form of the dielectric permittivity of
BN whose peak is larger than SiC’s one, this source
is less coherent than those based on SiC. However,
it shows that it is possible to obtain other coherent
thermal sources based on the same principle, with
other materials and on other wavelength ranges. It
also gives interesting ideas to greatly improve theses
sources coherence by controlling and tuning the polar
materials (such as SiC and BN) dielectric permittivi-
ties (making the peaks narrower for example).
NANOSTRUCTURES THERMAL EMISSION OPTIMIZATION USING GENETIC ALGORITHMS AND PARTICLE
SWARMS
223

Figure 9: Spectral and directional emissivity and reflectivity
for TM and TE polarizations of a bilayer structure made of
a 450nm thick Ge layer and a 310nm thick BN layer.
4 CONCLUSIONS
It was shown in this paper that evolutionary opti-
mization methods (genetic algorithms and particle
swarms) can be very helpful for the inverse design
of complex nanostructures with peculiar properties.
It was possible to design multilayer nanostructures
with coherent thermal emission in the mid infrared
region in spite of a relative ignorance of the pre-
cise physical phenomena underlying such properties.
The same optimization methods helped in simplify-
ing these sources to finally obtain Ge − SiC bilayer
structures, which are, to our knowledge, the simplest
existing structures with such features. The simplicity
of the resulting objects, made possible an analytical
study and the understanding of their internal function-
ing. This allows a more rational design of of new co-
herent thermal sources emitting in other wavelength
ranges. Optimization algorithms are being improved
to implement multi-objective optimization and make
more systematic the design and simplification of ther-
mal sources in mid and near infrared regions, with a
big variety of materials.
ACKNOWLEDGEMENTS
Elyes Nefzaoui thanks Jacques Nrault, Manuel Gi-
rault and Younes Ezzahri for helpful discussions.
REFERENCES
Ben-Abdallah, P. and Ni, B. (2005). Single-defect bragg
stacks for high-power narrow-band thermal emission.
J. Appl. Phys., 97:104910.
Celanovic, I., Perreault, D., and Kassakian, J. (2005).
Resonant-cavity enhanced thermal emission. Phys.
Rev. B, 72:075127.
Drevillon, J. (2007). Design ab-initio de mat
´
eriaux micro et
nanostructur
´
es pour l’
´
emission thermique coh
´
erente
en champ proche et en champ lointain. PhD thesis,
Universit
´
e de Nantes.
Drevillon, J. and Ben-Abdallah, P. (2007). Ab initio de-
sign of coherent thermal sources. J. Appl. Phys.,
102:114305.
Enoch, S., Tayeb, G., Sabouroux, P., Gurin, N., and Vincent,
P. (2002). A mtamaterial for directive emission. Phys.
Rev. Lett., 89:213902.
Fu, C. J., Zhang, Z. M., and Tanner, D. B. (2005). Planar
heterogenous structures for coherent emission of radi-
ation. Opt. Lett., 30:1873.
Greffet, J. J. and Carminati, R. (1999). Near-field effects in
spatial coherence of thermal sources. Phys. Rev. Lett.,
82:1660–1663.
Greffet, J. J., Carminati, R., Joulain, K., Mulet, J. P., Main-
guy, S., and Chen, Y. (2002). Coherent emission of
light by thermal sources. Nature, 416:61–64.
Joulain, K. and Loizeau, A. (2007). Coherent thermal
emission by microstructured waveguides. JQSRT,
104:208.
Lee, B. J., Fu, C. J., and Zhang, Z. M. (2005). Coher-
ent thermal emission from one-dimensional photonic
crystals. Appl. Phys. Lett., 87:071904.
Palik, E. D. (1998). Handbook of optical constants of solids.
Academic Press, London.
Richter, K., Chen, G., and Tien, C. L. (1993). Partial coher-
ence theory of multilayer thin-film optical properties.
Opt. Eng., 32:1897–1903.
Sai, H., Yugami, H., Akiyama, Y., Kanamori, Y., and Hane,
K. (2001). Spectral control of thermal emission by
periodic microstructured surfaces in the near-infrared
region. J. Opt. Soc. Am. A, 18:1471–1476.
Shchegrov, A. V., Joulain, K., Carminati, R., and Gref-
fet, J. J. (2000). Near field spectral effect due to
electromagnetic surface excitations. Phys. Rev. Lett.,
85:1548–1551.
Zhang, Z. M. (2007). Nano/microscale Heat Transfer.
McGraw-Hill, New York.
ICEC 2010 - International Conference on Evolutionary Computation
224