OPTIMAL VIABLE PATH SEARCH FOR A CHEESE RIPENING

PROCESS USING A MULTI-OBJECTIVE EA

Salma Mesmoudi, Nathalie Perrot

UMR782 G

enie et Microbiologie des Proc

es Alimentaires. AgroParisTech, INRA, 78850 Thiverval-Grignon, France

Romain Reuillon, Paul Bourgine

ISC-PIF, CNRS CREA, UMR 7656, Paris, France

Evelyne Lutton

INRIA - Saclay-Ile-de-France, AVIZ team, Orsay, France

Keywords:

Multiobjective evolutionary algorithm, Viability modeling, Optimal path search, Indirect encoding, Agri-food

process modeling, Cheese ripening.

Abstract:

Viability theory is a very attractive theoretical approach for the modeling of complex dynamical systems.

However, its scope of application is limited due to the high computational power it necessitates. Evolutionary

computation is a convenient way to address some issues related to this theory. In this paper, we present a multi-

objective evolutionary approach to address the optimisation problem related to the computation of optimal

command proﬁles of a complex process. The application we address here is a real size problem from dairy

industry, the modeling of a Camembert cheese ripening process. We have developed a parallel implementation

of a multiobjective EA that has produced a Pareto front of optimal control proﬁles (or trajectories), with respect

to four objectives. The Pareto front was then analysed by an expert who selected a interesting compromise,

yielding a new control proﬁle that seems promising for industrial applications.

1 INTRODUCTION

In this paper, we consider a multi-objective optimisa-

tion problem related to the modeling of an agri-food

industrial process, that is the camembert cheese ripen-

ing process. Experimental and analytical approaches

allow to build a set of models that reﬂect the nu-

merous interactions that take place at different scales,

from microscopic to macroscopic levels. These mod-

els are combined into a single complex one, that is

exploited via as a so-called viability analysis.

Viability theory considers the problem of main-

taining a system under a set of constraints (Aubin,

1991). To solve viability problems one generally

builds a viability kernel, which is the set of initial

states from which there exists a trajectory that remains

in the set of constraints. This theory is very conve-

nient to model complex systems, but current numer-

ical applications are limited due to the high compu-

tational power it necessitates. A question currently

addressed by the community is the computation of

a viability kernel, and various approaches now exists

(Bokanowski et al., 2006).

We deal here with another critical problem related

to the application of this theory, which is how to prac-

tically use a viability kernel once it has been com-

puted. A question that needs to be addressed is the

one of ﬁnding an optimal path within the viability ker-

nel. By optimal path we mean a set of control param-

eters and commands that guides the dynamical system

toward a desired target state (that is, in the case of a

cheese, a desired target weight and quality). We will

see in the sequel that it can be formulated as a multi-

objective optimisation problem.

The paper is organised as follows. Section 2 de-

scribes some basic principles of a viability analysis

applied to cheese ripening modeling, and describes

the optimisation problem that has to be solved. Then

the OpenMOLE platform on which algorithms have

been developed, is described in section 3. Section 4

225

Mesmoudi S., Perrot N., Reuillon R., Bourgine P. and Lutton E..

OPTIMAL VIABLE PATH SEARCH FOR A CHEESE RIPENING PROCESS USING A MULTI-OBJECTIVE EA.

DOI: 10.5220/0003083902250230

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 225-230

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

presents the details of the algorithm that has been de-

veloped: it is based on an indirect encoding of a path

in the viability graph. Experimental setup and results

are given in section 5. An analysis of the optimal tra-

jectory is then made by a cheese-ripening expert in

section 5.3, before concluding (section 6).

2 VIABILITY ANALYSIS OF AN

INDUSTRIAL CHEESE

RIPENING PROCESS

Industrial cheesemaking of camembert is based on the

use of pasteurized milk, and on a ripening process

conducted in controlled chambers, in order to obtain

a product at a given (savety and quality) target.

A camembert type cheese is made by in-

oculating milk with lactic acid bacteria (Flora

Danica lyophilisate, CHN11, Chr Hansen, Arpa-

jon, France), and other speciﬁc microorganisms

like Kluyveromyces marxianus (GMPA collection,

448), Geotrichum candidum (Degussa,D), Penicil-

lium camemberti (Degussa,R), and Brevibacterium

aurantiacum (ATCC9175) as ripening ﬂora. After co-

agulation and cutting, it is then shaped in moulds. Af-

ter drained (around 24h), fresh cheese is obtained and

transfered in the ripening chamber. At this stage, each

cheese weights around 300g. The cheeses are then left

for ripening for at least 3 weeks, in order to obtain to

obtain (1) a limited mass loss and at the same time

(2) a given quality of coat of the rind and a creamy

texture, due to an optimum microorganisms behavior.

For modeling purpose, we consider here a criti-

cal phenomenon for industrials which is the cheese

mass loss during the ripening process. It is linked in a

complex way to evaporation and to carbon consump-

tion due respiration of micro-organisms in the ripen-

ing chamber (Helias et al., 2007), for instance:

• Low relative humidity and high temperature on

the cheese surface increases evaporation.

• Cheese surface temperature decreases when evap-

oration occurs.

• Respiration increases the cheese surface temper-

ature as heat is produced during the substrate

degradation.

The state variables that have then been chosen to

build the viability kernel are:

• the cheese mass, with a range from 250g to 310g

with steps of 1g,

• the cheese temperature from 8

◦

C to 16

◦

C (step

◦

• the respiration rate of micro-organisms from 0 to

50 g/m

/day (step 1g/m

/day).

Additionnally, the control variables are

• the ripening room temperature (from 8

◦

C to 16

◦

C, step 1

◦

C),

• the relative humidity (from 84% to 98%, step 2%).

The viability kernel is deﬁned by the following

constraints:

• The ripened cheese should have at the end of the

process a mass between 250−270g, a temperature

between 8

◦

− 10

◦

C and a respiration between 23

and 50g/m

/day.

• The (CO

) gas rate evolution should follow

a speciﬁed proﬁle along the process, in order

to fully exploit the micro-organisms capabilities.

This constraint is set by experts. The respiration

rate should begin at level 0 on day 1 (microbial

growth latency), reaches a maximum between day

3 and day 8 and decreases slowly during the last

days of ripening (see (Sicard et al., 2009) for more

details).

On the basis of this model, a viability kernel has

been calculated (Sicard et al., 2009). Coupled to this

calculus, a geometric analysis of the shape of the vi-

ability kernel, and of all the viable paths to the target

(also named the viability tube), provides useful infor-

mations about the robustness and uncertainties of the

system. This analysis is based on the computation of

the boundaries of the viability tube, and for each point

of the tube, on its distance to the nearest boudary. Op-

timal algorithms for the Euclidean distance transform

(EDT) in arbitrary dimension have been developed for

morphological mathematics and image analysis pur-

pose. (Mesmoudi et al., 2009) adapted one of these

algorithms (Coeurjolly and Montanvert, 2007) for the

analysis of viability tube data.

The aim is to ﬁnd an optimal strategy, i.e. an op-

timal and real path, among each possible viable path

to the target. However each trajectory in the viabil-

ity tube can be evaluated according to four goals :

loss mass minimisation, number of control changes,

trajectory robustness and optimal breath evaluated by

the time to reach the maximal respiration rate. Con-

venient algorithms for that purpose are thus multi-

objective optimisation ones.

Multi-objective optimisation problems are often

NP-hard, complex and CPU time consuming. Exact

methods can be used to ﬁnd the exact Pareto front (or

a subset of the front), but usually it is impossible to

compute exact solutions for large problems, as they

are time and memory consuming. For instance, for

the cheese ripening case, there exists 10

possible

trajectories in the viability kernel we deﬁned.

ICEC 2010 - International Conference on Evolutionary Computation

226

Figure 1: The viability graph calculated for 12 days of

ripening. The time, respiration rate and cheese weigth vi-

able value for each days are represented.

We rely in this work on the use of multi-objective

Evolutionary Algorithm (EA) to approximate Pareto

fronts within a reasonable computation time. Addi-

tionnally, as the cheese mass loss modeling is actually

a large sized problem, the algorithms have been im-

plemented on a parallel and distributed computation

grid.

Our problem corresponds to a search for an opti-

mal path in a graph, where each node represents the

state of the cheese (mass and breath) and each edge

represents a control (relative humidity and chamber

temperature). The graph is organised as a succession

of slices, each representing a day, it is therefore not

complete.

3 PARALLEL

IMPLEMENTATION

In this paper, we deal with a grid of computers (mul-

ticomputers architecture), a multiple-population (or

multiple-deme) structure is more convenient. These

algorithms maintain several subpopulations that oc-

casionally exchange individuals (during a migration

step). Additionnally, we choose to use the multiob-

jective approach proposed by (Horn et al., 1994) and

(Deb et al., 2000): Nondominated Sorting Genetic Al-

gorithm (NSGA) and NSGAII.

Our implementation is based on the OpenMOLE

platform of ”workﬂow” (Reuillon et al., 2010). The

development of OpenMOLE was organized under

the form of a community of free software pro-

grams that is today very active. OpenMOLE is a

framework providing distributed computing facilities.

It takes advantage of generic interface of JSAGA

(http://grid.in2p3.fr/jsaga/) and provides on

top of that. OpenMOLE has been designed to work

out of the box on the user desktop with the idea of

completely hiding the fact that computation may be

carried out on distributed environments.

4 ALGORITHM

The NSGA-II algorithm is based on a ranking that

shares the population into several classes at each gen-

eration (see (Deb et al., 2000) for more details).

4.1 Search Space, Solutions Encoding

The Camembert ripening process can be described via

a graph, where each node is a viable state, i.e. a point

in a space of dimension 3: mass(M) (in g), breathing

(R) (in g/m

/day) and time (i) (in days of ripening).

This graph is oriented with respect to time. It is in-

complete since every state cannot be connected to all

others states. Usually, for every viable state there ex-

ists k outgoing edges, or controls, such as 1 ≤ k ≤ 74.

Every viable state E

such as 2 ≤ i ≤ N is at least

connected by two oriented edges:

i−1

,i−1

→ E

i+1

,i+1

to each edge (→) corresponds a control pair C

: that

represents the relative humidity and the ripening room

temperature to be applied to obtain the connected

node (objective state), for instance E

i+1

,i+1

from

A ﬁrst question to address now is how to encode

a viable path in a genome and respect the various va-

lidity constraints. A direct encoding is for instance

an ordered list of states, that represent the successive

states of a camembert during its ripening. Each state

change, that corresponds to an edge of the viability

graph, is characterised by its controls C

. This rep-

resentation has however an important drawback, as it

becomes difﬁcult to maintain a set of valid solutions

after the application of genetic operators.

We thus preferred an indirect encoding, i.e. to en-

code the way a graph is built instead of encoding the

graph itself. Any viable path can be specifyed, by its

initial state and by a set of successive controls. But,

as the the number of outgoing controls/edges may be

different for each state, it has been necessary to built

an ad-hoc addressing that is valid whatever the state.

Let C

= C

,...,C

be the set of possible out-

going control pairs for the state E

(k is variable

and depends on the current state). To specify a given

edge it is thus enough to provide an index that identify

the edge in the set C

A robust way to do this, while ensuring a valid

edge is uniquely identiﬁed at each state, is to use an

edge addressing based on real numbers, as follows.

Let S = {p(C

), p(C

),.., p(C

)} be a set of reals of

[0,1] where each p(C

) represents a proportion, or per-

centage that is interpreted with respect to the number

of outgoing edges of the state E

. For instance, if in a

state E

has 10 outgoing edges, then if p(C

) belongs

OPTIMAL VIABLE PATH SEARCH FOR A CHEESE RIPENING PROCESS USING A MULTI-OBJECTIVE EA

227

to [0,

] it represents the ﬁrst edge, the second one if

it belongs to ]

], so on until ]

n−1

] for the last

edge. The edges are ordered using the values of the

associated control pair (humidity and temperature).

4.2 Fitness Functions, Pareto

Optimality

An optimal ripening path can be deﬁned with respect

to four objectives:

1. mass loss, to be minimised

2. number of control changes, to be minimised,

3. trajectory robustness, to be maximised,

4. number of days to get the maximum of respira-

tion, to be minimized.

This problem is a typical multiobjective optimisation,

usually deﬁned as follows.

”min/max”z = f (x) = ( f

(x), f

(x),..., f

(x)) ∈ R

with x = (x

,...,x

) ∈ X, an n − dimensional vec-

tor, and X the search space. f

are partial evaluations

of the solution, usually corresponding to contradic-

tory aims. The optimal solutions correspond thus to a

set of compromise between the m various partial eval-

uations. In other words, the Pareto optimal set X

∗

is made of all non-dominated points, i.e. points for

which it is impossible to improve any objective with-

out simultaneously worsening another:

∗

= {x

∗

∈ X| 6 ∃x ∈ X, f (x) ≤ f (x

∗

)},

where f (x) ≤ f (y) ⇐⇒ ∀i ∈ 1..m, f

(x) ≤ f

(y)

and ∃ j ∈ 1..m, f

(x) < f

(y)

4.3 Genetic Engine

• Selection and elitism: Among the various selec-

tion operators that have been proposed in the lit-

erature (see for instance (Goldberg, 1989)), we

choose to use a tournament selection, due to its

parsimonious mechanism that only considers a

small random subsample of the population. Ad-

ditionnally, comparisons are based on both domi-

nation and crowding criteria (Tsai et al., 2002).

• Crossover: In the case of a direct coding, i.e.

when the path is encoded as a set of succes-

sive states, it becomes necessary to repair in-

valid genomes after crossover. There exists var-

ious solutions in the literature to cope with order-

based encodings, like cycle crossover (Oliver

et al., 1987), partially matched crossover (Gold-

berg, 1989) and order crossover (Goldberg, 1989),

(Davis, 1985).

However, the indirect encoding we propose in sec-

tion 4.1 allows to directly use simple crossovers

such as the uniform crossover (UX) (Syswerda,

1989) and arithmetic crossover (AX) (Eiben and

Smith, 2003).

• Mutation: In this work we used a basic random

mutation.

5 RESULTS

5.1 Parameters Setting

The parameter values were set heuristically. Addi-

tionally, as the computational load is high (around

8 hours using a computionnal grid) we did not per-

form a comprehensive study on the inﬂuence of dif-

ferent parameter settings, and it is possible that a care-

ful ﬁne-tuning of some values could bring slight im-

provements to the achieved results. For all experi-

ments, the parameter setting is given in table 1.

5.2 Numerical Results

The Pareto front that has been estimated is made of

142937 trajectories, however, with respect to the ob-

jectives, they correspond to only 329 combinations

(see ﬁgure 2). A principal component analysis (PCA)

was performed on the Pareto front obtained using our

implementation. The PCA was based on the follow-

ing variables: mass loss minimisation, number of con-

trol changes, trajectory robustness and optimal breath

evaluated by the time to reach the maximal respiration

rate. The ﬁrst two eigenvectors represent 45.35% and

28% of the total variance, respectively. The variable

projection and the distribution of the Pareto front so-

lutions are represented in Figure 2. we can notice that

the objective space is diversiﬁed: several solutions are

associated to each objectif.

5.3 Analysis

This Pareto front has been analysed by a cheese ripen-

ing expert, who selected an efﬁcient optimised trajec-

tory (PT) for a 0.280 kg cheese. The controls of this

trajectory are presented in table 2.

The optimised trajectory (PT), has been compared

to a viable trajectory (TVA) computed in a 8-day via-

bility kernel and already applied a pilot (Sicard et al.,

2010), and to a standard one (SRT) running in 12-

day and used in dairy industry. This TP trajectory

differs from the TVA trajectory and from the classical

one. The relative humidity is not constant like in TVA

ICEC 2010 - International Conference on Evolutionary Computation

228

Table 1: Parameters setting.

Population size 10 000

Crossover rate UX 0.1

AX 0.1

Mutation rate inversion 0.7

random 0.1

Stopping criterion max number of evaluations 10 000000

max number of evaluations without improvement 10000

Number of replication 1000

Table 2: Summary of controls (temperature T

◦

and relative

humidity RH% ) applied to the optimised trajectory PT, the

viable trajectory TVA , and a standard trajectory SRT.

◦

value RH% value

Day PT TVA SRT PT TVA SRT

1 12 12 12 84 84 92

2 11 13 12 96 94 92

3 14 14 12 95 94 92

4 14 14 12 95 94 92

5 14 12 12 95 94 92

6 9 12 12 96 94 92

7 9 9 12 96 94 92

8 - - 12 - - 92

9 - - 12 - - 92

10 - - 12 - - 92

11 - - 12 - - 92

Figure 2: Projection of Pareto front solutions using a prin-

cipal component analysis (PCA).

(94%) or in the standard SRT trajectory (92%) (table

2). However, like in TVA (table 2) the temperature

control varies whereas in the standard trajectory it re-

mains constant. To analyse the consequences of these

PT trajectory control changes, we compare its cheese

mass loss evolution and respiration rate to those of

TVA and standard trajectories.

Figure 3 shows the expected mass loss during the

PT trajectory compared to the mass loss during the

Figure 3: Comparison of cheese mass loss between PT tra-

jectory (computed values), and TVA and SRT ones (mea-

sured values from real experiments in a ripening chamber).

TVA and SRT trajectories. The quantities that are

displayed are computed for PT, and measured during

an experimental real simulation in a ripening chamber

for TVA and SRT. The mass loss is 0.013 kg for the

PT trajectory, while it is of 0.034 kg for the TVA tra-

jectory and of 0.054 kg for the standard ripening. This

result is signiﬁcative, as a minimisation of mass loss

is a very challenging issue for the dairy industry. This

small mass loss can be explained by the high values

of relative humidity of the PT trajectory. The cheese

mass at the end of the robust ripening remains within

the desired target range (0.25 kg to 0.27 kg).

Nevertheless, the mass loss is not enough to assess

the quality of a cheese ripening process. Mass loss is

a very sensitive parameter (a mass can be lost in a

dried atmosphere in a few days only), but it is not the

only one. If the other phenomena are not correctly

controlled, ripening may not be satisfying. The mi-

crobial activities of optimized (PT), viable (TVA) and

standard (SRT) ripening processes were also com-

pared, and the results are presented in Figure 4. The

respiration rate is the only kinetic that was checked.

As shown, the respiration rate starts at 0, reaches a

maximum of over 40 g/m

/day, and then slowly de-

creases until the day the cheese is wrapped. The max-

imum respiration rate begins two days earlier in the

PT ripening process than in the standard ripening pro-

OPTIMAL VIABLE PATH SEARCH FOR A CHEESE RIPENING PROCESS USING A MULTI-OBJECTIVE EA

229

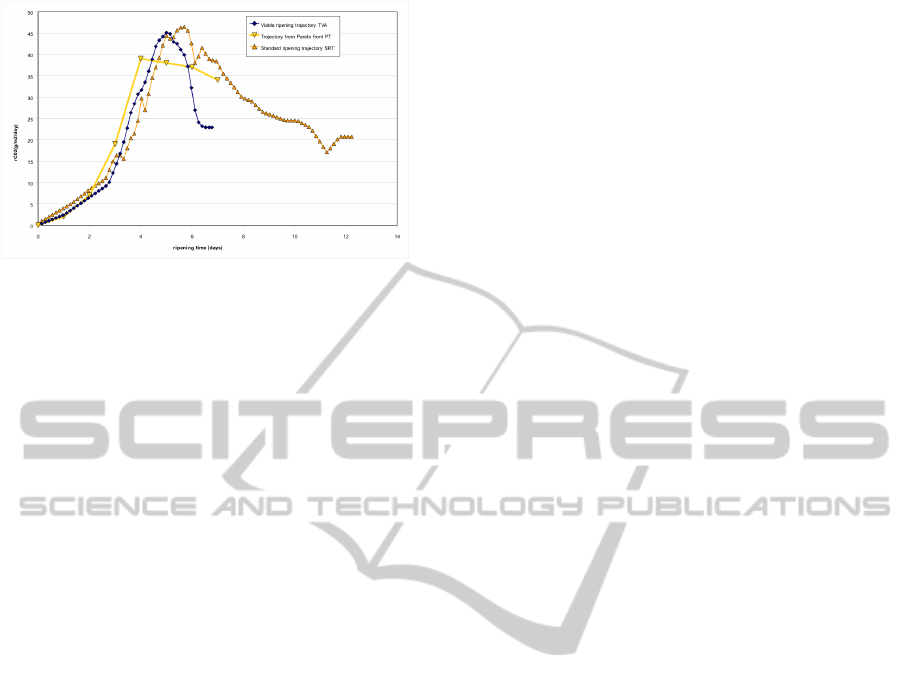
Figure 4: Comparison of respiration rates between PT tra-

jectory (computed values), and TVA and SRT ones (mea-

sured values).

cess, and one day and a half ealier in the TVA ripening

process.

We can therefore conclude that the PT ripening

process is very similar to the TVA one.

6 CONCLUSIONS

In this work, we used a parallel multi-objective evo-

lutionary algorithm to model a cheese ripening pro-

cess. Based on viability theory, the analysis yield a

Pareto front of a set of viable trajectories. A analy-

sis made by a cheese ripening expert allowed to select

an interesting trajectory in this Pareto set. The major

improvement of this optimal controlled trajectory is

its shortening, which is in accordance with previous

work on this topic. It has been experimentally ver-

iﬁed that a 8 days trajectory (the TVA trajectory of

ﬁgure 3 and 4) was able to yield a similar cheese in

terms of sensory panel (Sicard et al., 2010) in compar-

ison to the standard trajectory used in cheese ripening

industry. Additionally, for the 8 days trajectory, the

simulated process yield quantities that seems coherent

with real experiments using expert-based optimised

control settings. Further work on this topic will con-

sist in using the Pareto optimal trajectory to control an

experimental ripening process, in order to verify the

precision and validity of the modeling.

REFERENCES

Aubin, J. P. (1991). Viability Theory. Birkhauser, Basel.

Bokanowski, O., Martin, S., Munos, R., and Zidani, H.

(2006). An anti-diffusive scheme for viability prob-

lems. Applied Numerical Mathematics, 56:1147–

1162.

Coeurjolly, D. and Montanvert, A. (2007). Optimal separa-

ble algorithms to compute the reverse euclidean dis-

tance transformation and discrete medial axis in arbi-

trary dimension. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 29(3):437–448.

Davis, L. (1985). Applying adapting algorithms to epistatic

domains. In Proc. int. joint conf. articial intelligence,

Quebec, canada.

Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T. (2000).

A fast elitist non dominated sorting genetic algorithm

for multi-objective optimization: Nsga-ii. In In M.

S. et al. (Ed.), Parallel Problem Solving from Nature

PPSN VI, Springer, pages 849–858.

Eiben, A. E. and Smith, J. E. (2003). Introduction to Evolu-

tionary Algorithms. Springer, Berlin.

Goldberg, D. (1989). Genetic algorithm in search, opti-

mization and machine learning, Machine Learning.

Addison-Wesley, New York26.

Helias, A., Mirade, P., and Corrieu, G. (2007). Modeling of

camembert-type cheese mass loss in a ripening cham-

ber. Main biological and physical phenomena Journal

of Dairy Science, 90:5324–5333.

Horn, J., Nafpliotis, N., and Goldberg, D. E. (1994). A

niched pareto genetic algorithm for multiobjective op-

timization. In In Proceedings of the First IEEE Con-

ference on Evolutionary Computation, IEEE World

Congress on Computational Computation, Volume 1,

Piscataway, NJ, IEEE Press, pages 82–87.

Mesmoudi, S. P., Alvarez, I., Martin, S., Perrot, N., and

Wuillemin, P.-H. (2009). Geometric analysis of a cap-

ture basin. application to cheese rippening process. In

Proceeding of the European Conference on Complex

Systems (ECCS).

Oliver, I., Smith, D., and Holland, J. (1987). A study of per-

mutation crossover operators on the traveling sales-

man problem. In Second int. conf. genetic algorithms,

volume 5, pages 224–230.

Reuillon, R., Chuffart, V., Leclaire, M., Faure, T., Du-

moulin, N., and Hill, D. (2010). Declarative task

delegation in openmole. In proceedings of Interna-

tional Conference on High Performance Computing

and Simulation (HPCS 2010).

Sicard, M., Martin, S., Rouillon, R., Mesmoudi, S., Al-

varez, I., and Perrot, N. (2010). Development of a

viability approach for reverse engineering in complex

food processes: Application to a camembert cheese

ripening process. geometric analysis for a reverse en-

gineering approach - part i. Food Engineering, sub-

mitted.

Sicard, M., Perrot, N., Baudrit, C., Reuillon, R., Bourgine,

P., Alvarez, I., and Martin, S. (2009). The viability

theory to control complex food processes. In Proceed-

ing of the European Conference on Complex Systems

(ECCS).

Syswerda, G. (1989). Uniform crossover in genetic algo-

rithms. In Schaffer, J. D. Proceedings of the Third

International Conference on Genetic Algorithms, San

Mateo, California, USA: Morgan, pages 2–9. Kauf-

mann Publishers.

Tsai, C., Tsai, C., and Yang, T. (2002). A modied multiple-

searching method to genetic algorithms for solving

traveling salesman problem. In In: IEEE int conf sys-

tems, Man and cybernetics, volume 3, pages 6–9.

ICEC 2010 - International Conference on Evolutionary Computation

230