
A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM
MOVEMENTS BASED ON PHYSIOLOGICAL INTER-JOINT
COUPLINGS
Till Bockemühl
1
and Volker Dürr
1,2
1
Dept. of Biological Cybernetics,
2
Cognitive Interaction Technology - Center of Excellence, CITEC
University of Bielefeld, PO Box 100131, 33501 Bielefeld, Germany
Keywords: Motor control, Motor synergies.
Abstract: Substantial evidence suggests that nervous systems simplify motor control of complex body geometries by
use of higher level functional units, so called motor primitives or synergies. Although simpler, such high
level functional units still require an adequate controller. In a previous study, we found that kinematic inter-
joint couplings allow the extraction of simple movement synergies during unconstrained 3D catching
movements of the human arm and shoulder girdle. Here, we show that there is a bijective mapping between
movement synergy space and 3D Cartesian hand coordinates within the arm’s physiological working range.
Based on this mapping, we propose a minimal control schema for a 10-DoF arm and shoulder girdle. All
key elements of this schema are implemented as artificial neural networks (ANNs). For the central
controller, we evaluate two different ANN architectures: a feed-forward network and a recurrent Elman
network. We show that this control schema is capable of controlling goal-directed movements of a 10-DoF
arm with as few as five hidden units. Both controller variants are sufficient for the task. However, end-point
stability is better in the feed-forward controller.
1 INTRODUCTION
The complex biomechanics of limbs like the primate
arm facilitates the generation of a remarkable variety
of dexterous and context-dependent behaviors.
However, the large number of degrees of freedom
(DoFs), e.g. ten DoFs of the human arm and
shoulder girdle, complicates the required neural
control. This issue is known as motor redundancy
problem (Bernstein, 1967).
Central nervous systems (CNS) seem to easily
overcome this problem. One proposed mechanism
used by the CNS for the solution of the redundancy
problem is the combination of several DoFs into a
small set of higher level functional control units,
typically referred to as movement synergies or
primitives. There is substantial evidence that this
general concept is realized in vertebrate nervous
systems in one way or another (for reviews see Flash
and Hochner, 2005, and Ting and McKay, 2007).
Because the complexity of the control problem
depends on the number of controlled variables, these
synergies can simplify the control of the limb. Here,
we propose and evaluate a synergy-based and
closed-loop control schema that can be implemented
as a modular artificial neural network.
Classical studies on human reaching movements
tended to search for global optimization parameters
like speed (Atkeson and Hollerbach, 1985), jerk
(Flash and Hogan, 1985), or torque change (Uno, et
al., 1989). Most, if not all of these studies were
based on well-controlled but strongly constrained
movement paradigms, such as center-out tasks with
planar movements and fixed shoulder position.
Although these studies identified movement
invariants, they did not specify models of how the
brain could use them to overcome the problem of
redundancy. Furthermore, these invariants are based
on predictive strategies, i.e. global parameters that
are optimized offline and prior to the actual
movement. In these strategies sensory feedback
during an ongoing movement plays only a minor
role.
In contrast, current concepts of goal-directed
behavior favor prospective strategies that (a)
explicitly take into account sensory feedback during
ongoing behavior and (b) define motor goals in a
task space that is then mapped to motor output
(Todorov, 2004). Both of these aspects are realized
220
Bockemühl T. and Dürr V..
A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL INTER-JOINT COUPLINGS.
DOI: 10.5220/0003084102200226
In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages
220-226
ISBN: 978-989-8425-32-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

in the approach we propose here: (a) It relies on
continuous sensory feedback and (b) exploits a small
set of movement synergies, which can be viewed as
a set of elementary motor tasks as each synergy by
itself defines a valid movement.
In a previous experiment (Bockemühl, et al.,
2010) we studied natural and unconstrained arm
movements during a catching task in a large portion
of the arm’s workspace and recorded 10-D joint
angular time courses thereof. Using principal
components analysis (PCA) for synergy extraction
we found that the distribution of recorded postures
that occur during movements can be described
efficiently by linear combinations of a set of three
inter-joint couplings. We also found that the
individual contributions of these kinematic synergies
varied systematically with catching position in
external (Cartesian) hand coordinates. Together with
the fact that three is the minimum number of
synergies for control of end-effector position in 3D,
this suggests that neural control of arm movements
may exploit a simple mapping between synergy
space and Cartesian space. Here, we show that the
mapping between synergy space and hand position is
bijective within a large physiological working range.
Based on the three movement synergies that
capture natural inter-joint couplings, we propose a
simple closed-loop control schema for a 10-DoF
limb consisting of shoulder girdle, upper and lower
arm and hand. All elements of this schema are
implemented as ANNs. We evaluate two alternative
ANN variants as central controller: a multilayer
feed-forward network and a recurrent Elman
network.
We show that both controller variants we
examine here can generate physiological trajectories
of goal-directed reaching movements, similar to
those found experimentally. The networks are also
capable of generating reaching movements towards
novel targets, as well as smoothly interpolating
between two different movements. Internal
recurrence in the Elman controller improves learning
of physiological training data. In contrast to the
multilayer feed-forward network, however, the
Elman controller shows a tendency to drift and fails
to maintain a resting posture that keeps the hand at
the target position.
2 MATERIAL AND METHODS
2.1 Kinematic Model
We use a 10 DoF kinematic model of the human
upper limb, i.e., arm and shoulder girdle. The model
comprises 4 segments corresponding to a collarbone
that moves the shoulder joint with 3 DoFs, a
shoulder joint that moves the upper arm with 3
DoFs, an elbow and lower arm with 2 DoFs, and a
hand with 2 DoFs. Segment lengths within the
model are adjusted individually for each one of nine
recorded human subjects (Bockemühl, et al., 2010).
Consequently, each set of 10 joint angles is
equivalent to a unique posture, and standard forward
kinematics can be used to calculate the hand position
(end-effector).
2.2 Inter-joint Coupling Gives Rise to
Movement Synergies
The inter-joint couplings found in natural human,
one-handed catching movements are equivalent to
the first three principal components (PCs) of 10-D
arm postures (Bockemühl, et al., 2010). Each PC
constitutes a movement synergy so that each posture
can be described by a linear combination of the
mean posture of the original data set and a weighted
sum of three movement synergies. Because the
kinematic model, mean posture, and movement
synergies are fixed for a given subject, any hand
position in 3-D Cartesian space can solely be
described by a 3-D vector of scores that scale the
contribution of each synergy (see Equation 1).
3
1
)()(
i
ii
tst vmp
(1)
Here, p(t) represents a 10-D posture at time t, m
is the mean posture, s
i
(t) is the score of the posture
p(t) on the i
th
synergy, and v
i
is the i
th
synergy.
Modulating the scores in a target-dependent manner
therefore generates target-dependent hand
trajectories.
2.3 Control Structure and Artificial
Neural Networks
Given the current hand position and a target
position, e.g., the position of a ball to be caught, our
main goal is to generate an appropriate time series of
postures that moves the hand from its current
position to the target. Appropriate means that hand
trajectories should match the measured ones. Since
natural movements are marked by substantial inter-
joint couplings, we propose a control structure that
exploits these natural inter-joint couplings (Fig. 1).
This control schema contains an ANN module
that implements motor synergies in the form of a
A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL
INTER-JOINT COUPLINGS
221

feed-forward network (called synergy network in
Fig. 1). This module maps 3-D score vectors onto
10-D posture vectors in analogy to Equation 1.
The output of the synergy network can be
described by
3
1i
ijijj
swmp
(2)
where w
ji
is the weight matrix which is equivalent to
the 3x10 loadings of the PCs and that are used as
motor synergies here. The controller compares the
target position vector with the current hand position
and calculates the score changes necessary to
minimize the difference. The result is added to the
current 3D score vector, thus updating the arm
posture for the next iteration.
We evaluate two different ANN controller
variants. The first is a two-layered feed-forward
network; the second is a recurrent Elman network
(Elman, 1990). Both ANNs are identical except for
the additional recurrent connections comprising the
context layer of the Elman network (Figure 1).
Owing to the small number of synergies, input
and output of the controller are minimal and
equidimensional: both the two input position vectors
and the output synergy scores are three-dimensional.
The output Δs of the two-layered feed-forward
network can be calculated by
6
σ
,
,7
,1 ,
11
n
out out in in
s
wwwwx
ji i
j
kkn kj
ji
(3)
Output of the recurrent Elman network can be
calculated by the Equations 4 and 5. First, the
intermediate output y
hidden
at time t has to be
determined by
6
,
,7
,
1
1
() () ( 1)
n
hidden in in cont hidden
ji i
j
hjhh
i
h
ytw wxtwyt
(4)
Then, the output Δs at time t can be calculated
according to
n
h
hidden
hhk
out
nkk
tywwts
1
,1,
)()(
(5)
The input vector x in Eq. 3 and 4 contains the
coordinates of the target position, tp, and the current
hand position, cp (see Fig. 1). σ(x) is a hyperbolic
tangent function used as sigmoid activation function
of the hidden layer.
Figure 1: Control schema with inserts showing the synergy
network (top insert) and two ANN controller variants
(bottom insert). Black structures only: two-layer feed-
forward network. Black and gray structures combined:
recurrent Elman network. For clarity, the number of
hidden units is set to 3 (h
1
to h
n
).
ICFC 2010 - International Conference on Fuzzy Computation
222
2.4 Network Training
Training data consist of a series of eight goal-
directed hand trajectories recorded during
experiments in which participants were instructed to
catch an approaching ball (Bockemühl, et al., 2010).
Each trajectory starts at one of two initial positions,
ends at one of sixteen target positions, and contains
25 time steps. Half of the data set (eight trajectories)
is used for training, the other half is used for testing
generalization (further eight trajectories). In order to
account for end-point stability, each trajectory is
extended by a leading initial phase of 5 time steps
during which the hand remains at the initial position,
and a trailing target phase of 10 time steps during
which the hand remains at the catching position. In
accordance, the target position tp is kept at the
initial position for 5 time steps and is subsequently
set to one of the 16 prospective catching positions
for the remaining trial.
The goal of the training is to find weight
matrices for the controller ANNs that generate
physiologically plausible hand trajectories towards
the target. The root mean squared error (RMSE)
between training trajectories and generated
trajectories was used as the evaluation function.
Weight matrix optimization was realized via the
Levenberg-Marquardt algorithm (Levenberg, 1944,
Marquardt, 1963) implemented in MatLab 7.10 (The
Mathworks). To avoid local minima, the training
was repeated 100 times, using different randomly
initialized weight matrices. As a main objective of
this study was to determine the minimal size of the
hidden layer, we tested ANNs with 3, 4, 5, 6 or 10
hidden units.
3 RESULTS
3.1 The Mapping between Synergy
Space and Cartesian Space is
Bijective
As our movement synergies are principal
components of the joint angle space, they describe
correlations between joint angles. Owing to the
PCA, these synergies are orthogonal to each other.
However, the mapping of synergy space into
Cartesian space involves non-linear forward
kinematics of the controlled arm and, therefore,
needs not be bijective: multiple postures, and
therefore synergy combinations, could result in the
same hand position. A bijective mapping is a
prerequisite for simple control of arbitrary point-to-
point movements though. To ensure that the
mapping allows arbitrary hand positioning within its
working range (surjective mapping) and that any
combination of synergies leads to distinct hand
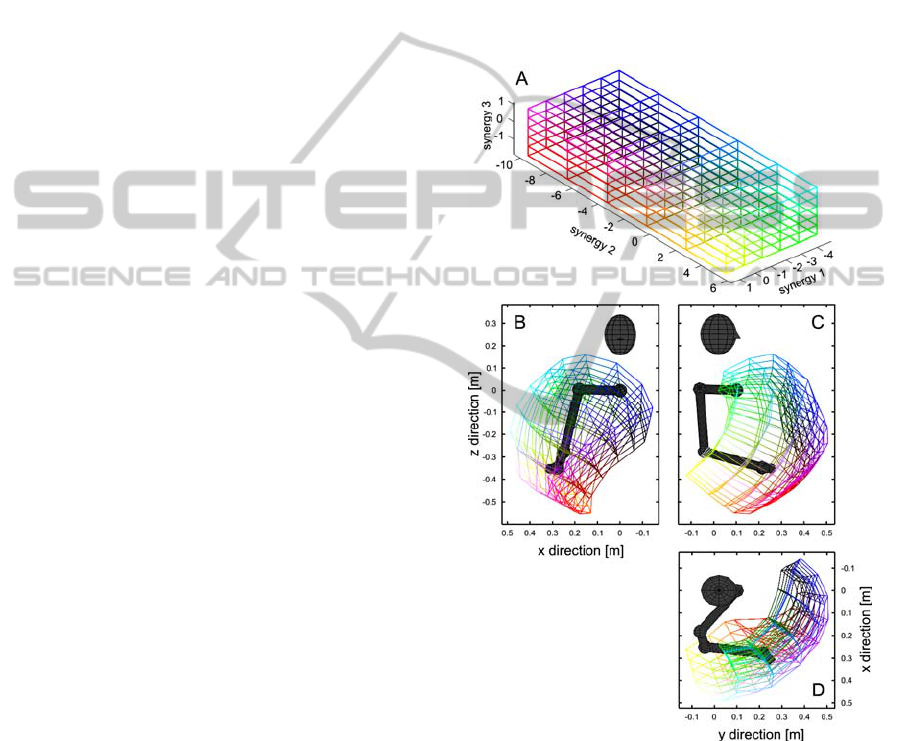
positions (injective mapping), Fig. 2 shows the
mapping of a 3D grid of synergy combinations into
Cartesian space of hand positions. Although the
mapping is non-linear, it covers a substantial
fraction of the physiological range of a human arm
(surjective) and the warped grid in Cartesian space
has no overlapping regions (injective).
Figure 2: Mapping between synergy space (A) and
Cartesian space (B, C and D) of the right human arm. B:
Frontal view. C: View from the right. D: Top view. The
kinematic model as well as a stylized head are depicted in
gray. Colors in synergy space correspond to the equivalent
color in Cartesian hand space and vice versa.
3.2 Training and Generalization
Performance
We find that both controller variants are able to
adapt to the training data. Figure 3 shows
A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL
INTER-JOINT COUPLINGS
223

representative results for training and generalization
performance, using data from a single subject and
initial position.
During training, the networks with more than
four hidden neurons reached RMSE values of less
than 20 mm, regardless of network type. Elman
networks with six or more hidden units even reached
values as low as 5 mm. However, generalization
performance leveled off at hidden layer sizes above
4 units. As generalization is as important as learning
performance on trained data, we used 5 hidden units
for both controller variants in all other experiments.
Figure 3: Performance of networks during training and
during generalization. A: performance of feed-forward
networks. B: performance of recurrent Elman network.
Figure 4: Representative trajectories during 40 time steps
generated by a feed-forward network (A and B) and an
Elman network (C and D) containing five hidden units. A
and C: trajectories to target positions encountered during
training. B and D: trajectories to novel target positions.
Red: trajectories generated by networks. Blue: trajectories
measured during experiment. At the same time, blue
trajectories seen in A and C are the training trajectories.
View from the rear right side of the kinematic model.
To illustrate overall controller performance,
Figure 4 shows representative trajectories produced
by a feed-forward network and an Elman network.
Whereas trajectories of both controller variants are
similar during the first half of the corresponding
movements, differences occur toward the end of the
trajectory. Here, the feed-forward network produces
a small, terminal curvature in the vicinity of the
target position. In comparison, the terminal
trajectory of the Elman network shows less deviation
from the physiological reference data, except for a
small but distinct kink near the end.
3.3 End-point Stability
An important aspect of target-directed movement is
the ability to keep the end-effector at the target after
reaching it. We tested this ability of both controller
variants by extending the presentation of target
inputs by 70 time steps. A representative result is
depicted in Figure 5. The prolonged holding phase
emphasizes the differences in end-point stability.
The feed-forward controller is much better in
keeping the end-effector at the target, though the
spirals at the end of high trajectories indicate
damped oscillations of the posture, beginning with
an overshoot followed by a gradual decline towards
a stable endpoint. In contrast, the trajectories
generated by the Elman controller tend to terminate
in a drifting hand position, indicating a constant
error output that slowly accumulates. The Elman
controller seems not to be able to compensate for
errors that occurr after the target is reached.
Figure 5: End-point stability. A: Trajectories generated by
a feed-forward ANN variant after 110 time steps (see also
Fig. 4B). B: Trajectories generated by an Elman ANN
variant after 110 time steps (see also Fig. 4D).
4 DISCUSSION
We have shown that goal-directed movement of a
ICFC 2010 - International Conference on Fuzzy Computation
224

human-like limb consisting of arm and shoulder-
girdle can be modelled by a comparatively simple
closed-loop control schema that comprises small
neural network modules and physiological
movement synergies.
In classical studies, only artificial or reduced data
have been used as a basis for the training of neural
networks for motor control (e.g., Massone and Bizzi,
1989, Kawato, et al., 1990, Massone and Myers
1994, Karniel and Inbar, 1997). More recent efforts
to model reaching movements based on ANNs do
take a physiologically oriented approach (Koike, et
al., 2006, Choi, et al., 2009) but still somewhat
neglect the importance of motor primitives or
synergies.
In contrast, numerous studies find evidence in
favor of a modular organization of the nervous
system (e.g. Mussa-Ivaldi, et al., 1994, d'Avella, et
al., 2006). Although these studies propose potential
CNS structures that might be important for motor
primitives, these studies often keep silent with
regard to more concrete neural models and how
exactly movement modules might be combined in a
task- or goal-dependent manner in order to produce
meaningful behavior.
The approach presented here tries to
accommodate both aforementioned aspects: We
combine a connectionist approach based on ANNs
with experimentally observed movement synergies
during a natural reaching task. Combining several
DoFs within one synergies and thereby reducing the
complexity of the control problem allows us to
exploit a bijective mapping between movement
synergy space and task space.
Comparative evaluation of the two controllers
indicates that, for the present problem, the recurrent
Elman network is less appropriate, owing to
insufficient end-point stability. Given, that the
context layer could be interpreted as an internal
model, and that internal models are assumed to be an
important computational element central to nervous
motor control (Wolpert & Ghahramani, 2000), this is
somewhat surprising.
Another notable aspect of the control schema
presented here is the low number of necessary
neuronal units. A feed-forward network with five
hidden units seems to be sufficient for the task of
accurately controlling three movement synergies.
There are two possible explanations for this: On the
one hand, the dissociation of the neuronal substrate
into two distinct modules, i.e. into a controller ANN
and a synergy network, might be more efficient that
a monolithic architecture of similar size. On the
other hand, the approach described here is solely
based on joint angle kinematics and neglects a
further potential source of complexity:
transformation of movement kinematics into a
muscle activation pattern. Again, this transformation
is a one-to-many mapping and might exacerbate the
necessary computations.
REFERENCES
Atkeson, C. G., Hollerbach, J. M. (1985). Kinematic
features of unrestrained vertical arm movements. The
Journal of Neuroscience 5, 2318 – 2330.
Bernstein, N. (1967). The co-ordination and regulation of
movements. New York: Pergamon Press Ltd.
Bockemühl, T., Troje, N. F., and Dürr, V. (2010). Inter-
joint coupling and joint angle synergies of human
catching movements. Human Movement Science 29,
73 – 93.
Choi, K., Hirose H., Sakurai, Y., Iijima, T., Koike, Y.
(2009). Prediction of arm trajectory from the neural
activities of the primary motor cortex with modular
connectionist architecture. Neural Networks 22, 1214
– 1223.
d’Avella, A., Portone, A., Fernandez, L., Lacquaniti, F.
(2006). Control of Fast-Reaching Movements by
Muscle Synergy Combinations. The Journal of
Neuroscience 26, 7791 – 7810.
Elman, J. L. (1990). Finding Structure in Time. Cognitive
Science 14, 179 – 211.
Flash, T., Hochner, B. (2005). Motor primitives in
vertebrates and invertebrates. Current Opinion in
Neurobiology 15, 660 – 666.
Flash, T., Hogan, N. (1985). The coordination of arm
movements: An experimentally confirmed
mathematical model. The Journal of Neuroscience, 5,
1688 – 1703.
Karniel A., Inbar G. (1997). A model for learning human
reaching movements. Biological Cybernetics 77, 173 –
183.
Kawato, M., Maeda Y., Uno, Y., Suzuki R. (1990).
Trajectory formation of arm movement by cascade
neural network model based on minimum torque-
change criterion. Biological Cybernetics 62, 275 –
288.
Koike, Y., Hirose, H., Sakurai, Y., Iijima, T. (2006).
Prediction of arm trajectory from a small number of
neuron activities in the primary motor cortex.
Neuroscience Research 55, 146 – 153.
Levenberg, K. (1944). A method for the solution of certain
nonlinear problems in least squares. Quarterly Journal
of Applied Mathematics 2, 164 – 168.
Marquardt, D. W. (1963). An algorithm for least-squares
estimation of nonlinear parameters. Siam Journal on
Applied Mathematics 11, 431 – 441.
Massone, L., Bizzi, E. (1989). A neural network model for
limb trajectory formation. Biological Cybernetics 61,
417 – 425.
A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL
INTER-JOINT COUPLINGS
225

Massone, L., Myers, J. (1994). A Neural Network Model
of an Anthropomorphic Arm. IEEE Transactions on
Systems, Man, and Cybernetics [B] 26, 719 – 732.
Mussa-Ivaldi, F. A., Giszter, S. F., Bizzi, E. (1994). Linear
combinations of primitives in vertebrate motor control.
Proceedings of the National Academy of Sciences of
the United States of America 91, 7534 – 7538.
Ting, L. H., McKay, J. L. (2007). Neuromechanics of
muscle synergies for posture and movement. Current
Opinion in Neurobiology. 17, 622 – 628.
Todorov, E. (2004). Optimality principles in sensorimotor
control. Nature Neuroscience 7, 907 – 915.
Uno, Y., Kawato M., Suzuki R. (1989). Formation and
control of optimal trajectory in human multijoint arm
movement. Biological Cybernetics 61, 89 – 101.
Wolpert, M., Ghahramani, Z. (2000). Computational
principles of movement neuroscience. Nature
Neuroscience 3, 1212-1217.
ICFC 2010 - International Conference on Fuzzy Computation
226
