AN EFFICIENT IMPLEMENTATION OF A REALISTIC SPIKING

NEURON MODEL ON AN FPGA

Dominic Just, Jeferson F. Chaves, Rogerio M. Gomes and Henrique E. Borges

Intelligent Systems Laboratory, CEFET-MG, Av. Amazonas 7675, Belo Horizonte, MG, CEP 30510-000, Brazil

Keywords:

Spiking neural networks, Field programmable gate array (FPGA), Hardware design.

Abstract:

Hardware implementations of spiking neuron models have been studied over the years mainly in researches

focused on bio-inspired systems and computational neuroscience. This introduced considerable challenges for

researchers particularly in terms of the requirements to realise a efﬁcient embedded solution which may pro-

vide artiﬁcial devices adaptability and performance in real-time environment. Thus, programmable hardware

was widely used as a model for the adaptable requirements of neural networks. From this perspective, this

paper describes an efﬁcient implementation of a realistic spiking neuron model on a Field Programmable Gate

Array (FPGA). A network consisting of 10 Izhikevich’s neurons was produced, in a low-cost and low-density

FPGA. It operates 100 times faster than in real time, and the perspectives of these results in newer models of

FPGAs are promising.

1 INTRODUCTION

Hardware implementations of spiking neuron models

have been carried out by several researchers in or-

der to develop systems that present autonomy, such as

robots (Florian, 2006) (Floreano et al., 2006). These

implementations had also as motivation to develop a

model which presents high performance, adaptability

in real-time environment, as well as biological plausi-

bility (Maguire et al., 2007) (Thomas and Luk, 2009).

There are two aspects in the biological back-

ground to be considered: the function and the struc-

ture of the network. Unlike the classical approach of

artiﬁcial neural networks, in which these two aspects

are studied together, the present work aims solely to

reproduce the structure of a natural neural network,

according to recent studies. Research on the func-

tional aspect of the neural network is currently carried

on by the authors in other experiments (Soares et al.,

2010).

Studies in neuroscience have revealed, by means

of experimental evidences, that the cortex can be de-

scribed as being organized, functionally, in hierar-

chical levels, where higher levels would coordinate

sets of functions of the lower levels (Edelman, 1987)

(Hadders-Algra, 2000) (Izhikevich et al., 2004) (Fris-

ton, 2010). One of the theories that is in compliance

with these studies is the Theory of Neuronal Group

Selection (TNGS) proposed by Edelman (Edelman,

1987).

TNGS establishes that correlations of the local-

ized neural cells in the cortical area of the brain, gen-

erate clusters units denoted as: neuronal groups (clus-

ter of 50 to 10.000 neural cells), local maps (reen-

trant clusters of neuronal groups) and global maps

(reentrant clusters of neural maps). A neuronal group

(NG) is a set of tightly coupled neurons which ﬁre and

oscillates in synchrony. Each neuron belongs only

to a single neuronal group, which is spatially local-

ized and functionally hyper-specialized. According

to TNGS, NGs are the most basic structures in the

cortical brain, from which memory and perception

processes arise, and can been seen as performing the

most primitive sensory-effector correlations.

Presently, large scale implementations of neurons

based models have been studied mainly on FPGAs.

Thomas and Luk (Thomas and Luk, 2009) developed

a fully-connected network of spiking neurons based

on Izhikevich spiking model that could be simulated

at 100 times real-time speed. However, the synap-

tic weights and the input currents were represented in

ﬁxed-point format using 9 bits. Thus, it is possible to

observe that when a mechanism of plasticity (STDP)

is inserted, the whole structure of the system has to be

changed. In addition, Thomas and Luk used a high-

density FPGA which contributed to the implementa-

tion of a greater number of neurons.

The feasibility of using FPGAs for large-scale

344

Just D., F. Chaves J., M. Gomes R. and E. Borges H..

AN EFFICIENT IMPLEMENTATION OF A REALISTIC SPIKING NEURON MODEL ON AN FPGA.

DOI: 10.5220/0003084303440349

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages

344-349

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

simulations of the model according to Izhikevich in

(Izhikevich, 2003) was explored in (Rice et al., 2009).

A modularized processing element to evaluate a large

number of Izhikevich’s spiking neurons in a pipelined

manner was developed, which allowed an easy scala-

bility of the model to larger FPGAs. They utilized an

algorithm based character recognition on Izhikevich’s

model for this study. However, this system was not

completely implemented on FPGAs, but some mod-

ules of the algorithm were processes on a computer.

Basically, the aim of the strategy proposed in this

paper is to embed a network of neurons that presents

the same anatomical structure of a neuronal group,

as proposed by Edelman, in a Field Programmable

Gate Array (FPGA). This design is built using ﬂoating

point circuits and has provide high-speed processing

speed, i.e., real time processing. Floating point hard-

ware implementations are extremely resource inten-

sive and the number of neurons embedded in FPGA

depends on the efﬁciency in terms of the used re-

sources.

Real time processing of neuronal groups is also

extremely important in real world applications. Thus,

the implementation proposed in this paper runs a very

accurate simulation of the biological reality.

This high level of biological plausibility is due to

the model of neuron used (Izhikevich, 2004), and due

to the possibility of using any topology by setting the

right parameters, e.g., the synaptic connection matrix.

As a scientiﬁc contribution, the present work

presents, as standpoint for the implementation of an

suitable biologically plausible architecture of spiking

neurons. Moreover, as regards to the principles of bi-

ological operations on the coordination structure of

the TNGS, the solution can be applied in the valida-

tion of various hypothesis with which neuroscience is

concerned. This trend have established itself recently

in literature, given the difﬁculties in performing some

experiments in vitro. Another important contribu-

tion of this paper is the establishment of a technol-

ogy or technique to increase the efﬁciency of a pro-

grammable logic hardware through the minimization

of the area covered by logical circuits. The beneﬁts

of this research have also contributed to the neuronal

implantation area.

In section 2 we present the neuron model used

in this work. The neuron model should be compu-

tationally simple in order to make this implementa-

tion feasible. The hardware designs developed are

introduced, analyzed and discussed in Section 3. In

addition, this section shows a comprehensive under-

standing of how the circuit works. Finally, Section 4

concludes the paper and presents some relevant exten-

sions of this work.

2 IZHIKEVICH MODEL

According to (Izhikevich, 2007), the biologically

most accurate models of neurons simulate the con-

centrations of several types of ions. The most impor-

tant ions are sodium (Na

), potassium (K

), calcium

(Ca

) and chloride (Cl

−

). There are two important

mechanisms, which lead to a concentration asymme-

try:

• Passive redistribution: some ions can penetrate

the cell membrane.

• Active transport: ions are pumped into the cell by

ionic pumps.

Both of these mechanisms lead to concentration

gradients. A concentration gradient causes an elec-

tric potential between the inside and the outside of

the cell. In addition, there is one more factor to con-

sider getting a comprehensive model. Since some of

the channels are susceptible to the concentration of

the potential and of the ion concentration, the conduc-

tance of the ionic channels can vary heavily and in a

strong nonlinear way. The Hodgkin-Huxley Model in

(Izhikevich, 2007) summarizes all this effects in one

model of four coupled ordinary differential equations

of ﬁrst order. This set of differential equations shows

the highly nonlinear behaviour of the whole system.

The Hodgkin-Huxley model is one of the most impor-

tant models of neurons, however, it presents a high

computational cost, limiting the simulation of a net-

work with few neurons.

In contrast, Eugene Izhikevich (Izhikevich, 2003)

developed a model of spiking neurons that reproduces

the behavior of neurons very accurate, but with much

simpler equations and low computational cost, allow-

ing the simulation of networks with large numbers of

neurons. It consists of the following two dimensional

system of one quadratic and one linear differential

equation, each of ﬁrst order:

= 0.04v

+ 5v + 140 − u + I (1)

= a(bv − u) (2)

with the after-spike resetting

if v ≥ 30mV, then v = c and u = u + d (3)

In these equations, u and v are the states of the

systems where v represents the membrane potential

of the system and u represents a membrane recov-

ery variable. I is the input current from the outside

world and from other neurons in the network, which

are connected to this neuron. The variables a, b, c,

d are ﬁxed dimensionless parameters. Depending on

these parameters, the Izhikevich model can describe

AN EFFICIENT IMPLEMENTATION OF A REALISTIC SPIKING NEURON MODEL ON AN FPGA

345

regular spiking, intrinsically bursting, chattering, fast

spiking, thalamus-cortical and low-threshold spiking

neurons as well as resonators. Table 1 shows some of-

ten used values for the parameters for the Izhikevich

model.

Table 1: Izhikevich Parameters.

Parameters Typical values Possible values

a 0.02 [0.02;0.1]

b 0.2 [0.2;0.25]

c -65mV [-55;-65]

d 2 [2;8]

For fast computation, Izhikevich suggested a nu-

meric method to simulate the behaviour of spiking

neurons in his publication (Izhikevich, 2003). This

code implements the system of differential equations

by using a Runge-Kutta method and by dividing the

computation of v into two steps. It simulates a net-

work of 1000 neurons fed with a random input circuit

I outside. Having an algorithm, a simulation of a sin-

gle neuron is straightforward.

3 THE HARDWARE DESIGN

The ﬁrst attempt is a simple mapping of the simpli-

ﬁcation of Izhikevich’s MATLAB-code in hardware.

The simpliﬁcation used looks like following:

(1) a=0.02*ones(10,1); b=0.2*ones(10,1);

(2) c=-65*ones(10,1); d=2*ones(10,1);

(3) S=rand(10,10);

(4) v=-65*ones(10,1); u=b.*v;

(5) for t=1:1000

(6) I_outside=rand(10,1);

(7) fired=find(v>=30);

(8) I_neuron=zeros(10,1);

(9) I_neuron(fired)=1;

(10) v(fired)=c(fired);

(11) U(fired)=u(fired)+d(fired);

(12) I=I_outside+sum(S(:,fired),2);

(13) v=v+0.5*(0.04*v.ˆ2+5*v+140-u+I);

(14) v=v+0.5*(0.04*v.ˆ2+5*v+140-u+I);

(15) u=u+a.*(b.*v-u);

(16) end;

This MATLAB-code is the basic idea for con-

structing an integrated circuit as shown in Figure 1.

This circuit has two registers to store each of the states

v and u. The content of the memory is fed into compu-

tational unit ComputeStepV which performs the op-

erations on line 13 and 14 of the algorithm. Then,

the computational unit ComputeStepU performs the

operations on line 15 in the MATLAB-code. The

computational units support the resetting condition

on lines 10 and 11, too. The component checkSpike

Figure 1: This ﬁgure shows the structure of the circuit of

the MATLAB-code. This circuit consists of blocks, which

perform the function v = v +0.5(0.04 v

+5v +140− u +I)

with reset condition v = c and the function u = u + a (b v −

u) with reset condition u = u + d. The clock management

controls checkSpike and the registers (indicated with a short

line).

Figure 2: This ﬁgure shows the structure of the circuit be-

hind the computeStepU-block in Figure 1. The inputs u and

v are fed into the blocks, which compute step by step the

formula u = u + a (b v − u) with reset condition u = u + d.

A, b and d are constants, which were hard coded in the cir-

cuit.

checks the condition on line 7 on the MATLAB-code.

If there is a spike, it sets the output I outside to 1

according to line 8 and 9. A clock management-

block controls at which time the value of v should be

checked for a spike. It controls as well, at which time

which memory has to be written and at which time

a cycle ends. As there are two computational steps

of v = v + 0.5 (0.04 v

+ 5 v + 140 − u + I), this de-

sign can be more efﬁcient by using the block com-

puteStepV twice. Therefore, clock management is

programmed in a way, that the circuit reuses the block

ComputeStepV twice in order to calculate the code on

line 13 twice. To keep the hardware usage small, all

calculations in this project is done with single preci-

sion (32 bit).

To explain how the hardware is designed in de-

tail, Figure 2 shows the block ComputeStepU of Fig-

ure 1. The variables u and v are inputs of the system

and unew is the only output. A closer look into the

function ComputeStepU shows how the actual com-

putation works: In the multiplier mul1, v·b is calcu-

lated. After this the subtracter sub subtracts u from

the prior result. Then, v·b-u is calculated. This re-

sult is fed to the multiplier mul2 and then to the adder

add1. After this, unew is ready. The multiplexer is

needed to make it possible to perform the function

u=u+d, if the input from I outside is 1. Behind the

boxes clock management, ComputeStepV and check-

Spike, there are similar circuits.

In the ﬁrst design, the MATLAB-code was simply

implemented in hardware. As a result, only a limited

ICFC 2010 - International Conference on Fuzzy Computation

346

number of neurons could be implemented in hardware

due to the heavy use of the FPGA resources.

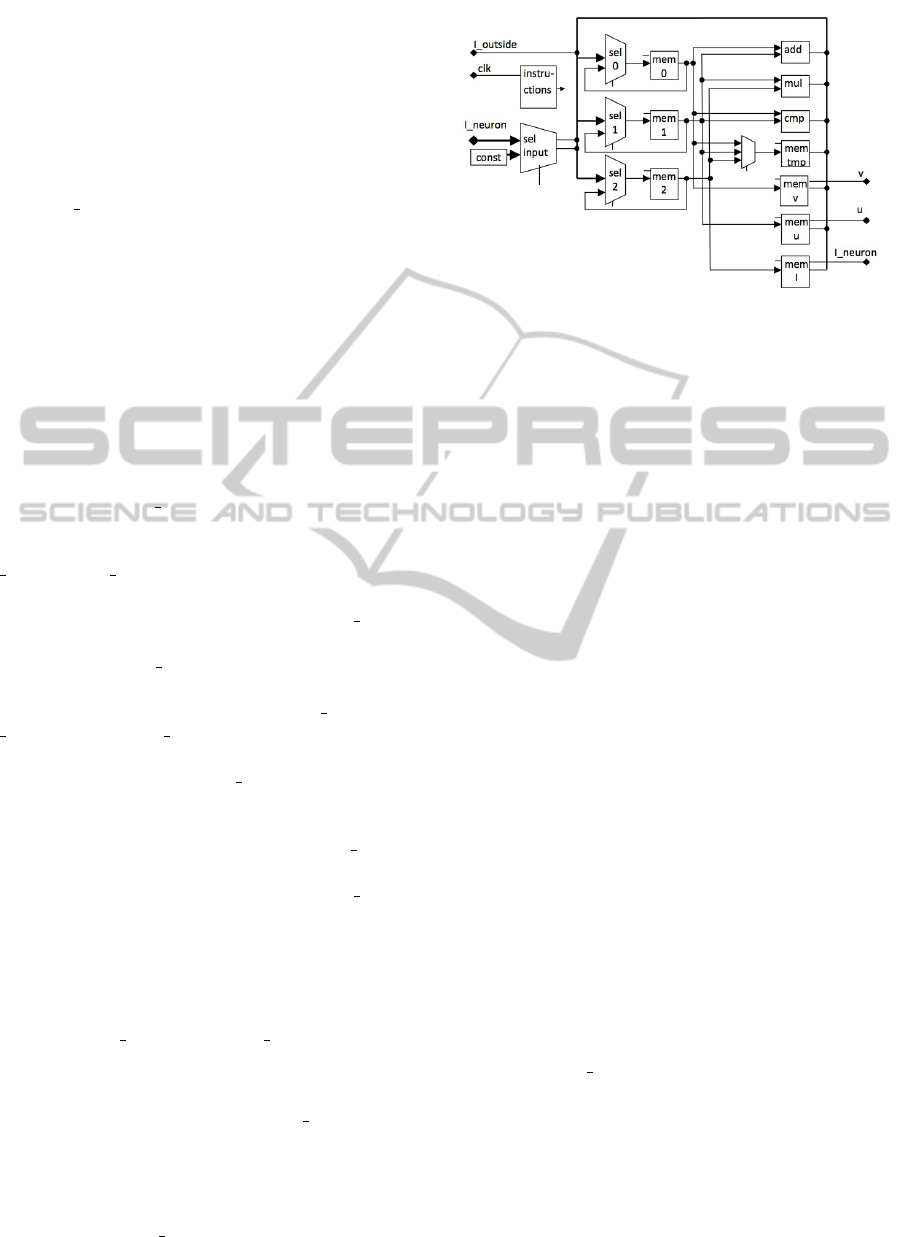
In order to improve the ﬁrst architecture a second

design was proposed. This new design consists in

building a computer-like circuit on an FPGA. Figure

3 shows the developed architecture where each wire is

32 bit wide, with exceptions of the 1 bit input clk, the

64 bit output of the instructions-block and of the 1 · n

bit input I neuron, where n is the number of neurons

in a neural network.

This circuit consists only of one instance of each

macrofunction. There is one adder (add), one mul-

tiplier (mul) and one comparator (cmp). There are 7

memories, as well. The most important ones are the

three 32 bit wide registers mem 0, mem 1 and mem

2 before the computing devices add, mul, cmp. The

values of these memories are the inputs of the compu-

tational blocks. They are as well the memories which

store the results of the output of the computational

blocks. The other memories mem v, mem u and mem

I store the states u and v of the system and the state

of the output spike I neuron. The memory mem temp

stores some temporary values to use them in further

computational steps. This circuit has the inputs clk,

I outside and I neuron.

The clk input is necessary for clocking some of

the system’s memories and macrofunctions. I outside

brings an input spike from the outside world to the

neuron. The input I neuron carries the input stimuli

generated by pre-synaptic neurons.

The reason for the distinction from I neuron and

I outside is because I outside can have any value and

is just added to the total current (code on page 3, line

6), whereas the input current I neuron from the other

neurons is either 0 or 1 (code on page 3, line 9) and

before adding I to get the input current for the formula

v = v+0.5(0.04v

+5v+140−u+I), each I neuron

has to be multiplied with a weight factor s

, which

represents the strength of the connection. I outside

counts other stimuli than the pre-synaptic (eg. noise).

This fact is also shown in the following formula,

where n represents the number of neurons in a neural

network:

I = I outside +

∑

i=0

· I neuron

(4)

The outputs v and u can be used to monitor the states

v and u of the neuron. The output I neuron is the

only important output of the neuron in the network

perspective. It gives the information, whether the neu-

ron spikes or not.

In a network of several neurons, it has to be con-

nected to the input I neuron of each other neuron in

the network.

Figure 3: This ﬁgure shows the datapath of one neuron. The

control paths are indicated by small lines. The control in-

formation come from the block Instructions. The bold lines

represent busses. The wires in this ﬁgure are 32 bit wide

with the exceptions of the one bit wide clock input clk and

the 64 bit wide control output from the Instructions-block.

There are ﬁve multiplexers in the circuit. The most

important ones are the three before the mem 0, mem

1 and mem 2. These multiplexers select one of their

inputs to feed it to their following memories. By do-

ing this, they select an operation or a memory. These

data will be stored in mem 0, mem 1 and mem 2 and

affect the system in the next cycle. The inputs to these

multiplexers are the following:

• The output of the memory after the multiplexer.

This source is selected, if the memory should not

change its value in a cycle. When the mem-

ory stores its next value, the same value is being

stored in the memory, which was already in the

memory.

• The result of the adder.

• The result of the multiplier.

• The output of the comparator.

• The output of mem v.

• The output of mem u.

• The output of mem I.

• The last 32 bits of the output of the instruction.

This operation is used to load a constant value to

the registers.

• The input I outside, which is the input from the

outside world to a neuron.

• The output of mem tmp.

• The ﬁrst output of the multiplexer sel input,

which contains the information whether predeces-

sor neurons spiked.

• The second output of the multiplexer sel input,

which contains the information about the weight

AN EFFICIENT IMPLEMENTATION OF A REALISTIC SPIKING NEURON MODEL ON AN FPGA

347

Figure 4: The Instructions-block is divided into the source

part and the time management part. The source part is a

memory, which gives an instruction for each value of PC.

The time management increases the PC after some clock

cycles in the clock wire. The number of clock cycles which

are necessary to increase the program-counter (PC) by 1 is

given by each instruction individually.

of the connection from another neuron to this neu-

ron. With this information, the input spike can be

calculated according to equation (4).

• Four inputs to select the parameters a, b, c, d.

The multiplexer Sel input has 2 outputs and 2·n in-

puts, where n is the number of neurons in a neural net-

work. For each neuron in the network, there are two

connections to the multiplexer sel input. One input

carries the information whether the predecessor neu-

ron spikes and one input carries the information, con-

taining the weight of the connection between the two

neurons. When summing up the input spikes from

other neurons, this multiplexer chooses a neuron, and

read in its spike. Then, it selects the next neuron, to

read in its spike and sum all spikes up according to

formula (4). The multiplexer next to mem tmp selects

which number (if any) should be stored in mem tmp.

The instructions-block provides the circuit with

instructions, which control what the circuit does. Fig-

ure 4 provides an overview of the Instructions-block.

The ﬁrst sub-block is the source-block. This block

consists of a memory, which is initialized with some

predeﬁned content before the circuit begins to run

and it is read only. The 7 bit program counter PC is

connected to the address input of the memory-block

source. For each value of PC, there is a 64 bit value on

the output of the source-block: The instruction. The

instruction is one of the outputs of the instructions-

block, but it is used in the time management-block as

well. In the whole circuit, only some parts of this 64

bit value are used to control the function of blocks,

memories and to control the multiplexers.

The time management is built of two functions.

The clock divider divides the clock by the 4 bit wide

number on its second input. So, the clock divider’s

output end instruction is a clock with a reduced fre-

quency. The counter-block increases its value after

each cycle of the end instruction. It starts with 0 and

counts up. The resulting output signal of the counter

is the program counter (PC), which affects the mem-

ory source. The output end instruction causes the

memories mem 0, mem 1 and mem 2 in Figure 3 to

store the next value. Since the end instruction wire

determines, when an instruction ends, a whole cycle

of end instruction is often just called cycle.

4 CONCLUSIONS

The ﬁrst attempt was straightforward to implement

and it was easy to understand the underlying func-

tion. But for the goal to implement a lot of neurons

in a relatively small FPGA, this model is not sufﬁ-

cient. The second model described in this paper is

much more efﬁcient, as it makes it possible to im-

plement a model of a neural network 10 times higher

than in traditional implementation. The limiting fac-

tor are the embedded multipliers. In this work, it is

not possible to create the desired macrofunctions just

out of logic and without the use of these multipliers.

However, the system computes much faster than real-

time. While designing this model, there was always a

focus on real-time compatibility, very important when

this network is needed to simulate a group of neurons,

which have to interact with the outside world.

All the designs in this paper work correctly. First,

the hardware design was logically validated with

Modelsim software, then was performed a timing

analysis with Altera TimeQuest software. After all

these software validations, the hardware was tested

in one Altera DE2 board containing one Cyclone II

FPGA, EP2C35F672C6, resulting in a computation

speed 109 times faster than real-time. The resource

usage of the circuit is very high since the processing

of ﬂoating point instructions is very resource inten-

sive, making a parallel simulation of more than 10

neurons impossible with the used device (low-cost Al-

tera FPGA). Table 2 shows the resource usage for of

the two models which were described in this paper. It

is important to emphasize that this work was imple-

ment on a low-cost and low-density FPGA Design.

There are some solutions to overcome the hard-

ware limitations: considering that the processing time

is only 10 % of the real time, each module might be

used 10 times, raising the number of neurons in the

network. Another possibility consists in using exter-

nal memories -containing large bandwidth- to store

the synaptic weights, as in the latest FPGAs models.

This work showed an efﬁcient hardware imple-

mentation of a neural model. The current implemen-

tation runs a very accurate simulation of the biologi-

cal reality. One of the results of this project is a neural

model consisting out of 10 neurons, 100 times faster

ICFC 2010 - International Conference on Fuzzy Computation

348

Table 2: Resource usage.

First implementation Second implementation Board ressources

Total combinatorial functions 7287 1664 33216

Registers 3819 755 33216

Embeded 9 bit multipliers 42 7 70

than real time, for further research and development.

However, higher density FPGAs with higher

bandwidth would make it possible to simulate larger

networks. The latest FPGA model from the same

manufacturer has 36 times more logical elements than

the device used in this work.

ACKNOWLEDGEMENTS

The authors would like to thank FAPEMIG for fund-

ing the project, the laboratory of intelligent systems

of CEFET-MG for the technical support and for mak-

ing available its infra-structure, which made this work

possible.

REFERENCES

Edelman, G. M. (1987). Neural darwinism: The theory of

neuronal group selection. Basic Books, New York.

Floreano, D., Epars, Y., Zufferey, J., and Mattiussi, C.

(2006). Evolution of Spiking Neural Circuits in Au-

tonomous Mobile Robots. International Journal of

Intelligent Systems, 21(9):1005–1024.

Florian, R. (2006). Spiking Neural Controllers for Pushing

Objects Around. LECTURE NOTES IN COMPUTER

SCIENCE, 4095:570.

Friston, K. (2010). The free-energy principle: a uni-

ﬁed brain theory? Nature Reviews Neuroscience,

11(2):127–138.

Hadders-Algra, M. (2000). The neuronal group selection

theory: a framework to explain variation in normal

motor development. Developmental Medicine and

Child Neurology, 42(08):566–572.

Izhikevich, E. (2003). Simple model of spiking neurons. In

IEEE transaction on neural networks.

Izhikevich, E. (2004). Which Model to Use for Cortical

Spiking Neurons? IEEE Transactions on Neural Net-

works, 15(5):1063.

Izhikevich, E., Gally, J., and Edelman, G. (2004). Spike-

timing dynamics of neuronal groups. Cerebral Cortex,

14(8):933.

Izhikevich, E. M. (2007). Dynamical Systems in Neuro-

science: The geometry of Excitability and Bursting.

MIT Press, Cambridge, London, ISBN 0262090430,

9780262090438, 441 pp.

Maguire, L., McGinnity, T., Glackin, B., Ghani, A., Bela-

treche, A., and Harkin, J. (2007). Challenges for large-

scale implementations of spiking neural networks on

FPGAs. Neurocomputing, 71(1-3):13–29.

Rice, K., Bhuiyan, M., Taha, T., Vutsinas, C., and Smith, M.

(2009). FPGA Implementation of Izhikevich Spiking

Neural Networks for Character Recognition. In 2009

International Conference on Reconﬁgurable Comput-

ing and FPGAs, pages 451–456. IEEE.

Soares, G. E., Borges, H. E., and Gomes, R. M. (2010).

Synthesis of Frequency Generator via Spiking Neu-

rons Network: a Genetic Algorithm Approach. In-

ternational Conference on Bio-Inspired Computing:

Theory and Applications.

Thomas, D. and Luk, W. (2009). FPGA accelerated sim-

ulation of biologically plausible spiking neural net-

works. In 2009 17th IEEE Symposium on Field Pro-

grammable Custom Computing Machines, pages 45–

52. IEEE.

AN EFFICIENT IMPLEMENTATION OF A REALISTIC SPIKING NEURON MODEL ON AN FPGA

349