REAL-TIME TRAJECTORY MODIFICATION
BASED ON BÉZIER SHAPE DEFORMATION
L. Hilario
1
, N. Montés
1
, M. C. Mora
2
and A. Falcó
1
1
Cardenal Herrera CEU University, C/San Bartolomé 55 46115, Alfara del Patriarca, Spain
2
Mechanical Engineering and Construction Department, Universitat Jaume I, Castellón, Spain
Keywords: Bézier, Deformation, Constrained optimization, Trajectory, Path planning, Artificial potential fields.
Abstract: This paper presents a new technique for flexible path planning based on the deformation of a Bézier curve
through a field of vectors. This new technique is called Bézier Shape Deformation (BSD). This deformation
is computed with a constrained optimization method (Lagrange Multipliers Theorem). The main advantage
of this method is how the solution is obtained. A linear system is solved to achieve the result. As a
consequence, the deformed curve is computed in a few milliseconds where the linear system can be solved
offline if the Bézier curve order is maintained constant during the movement of the robot. This method
allows the use of these trajectories in dynamic environments where the computational cost is critical. This
technique can be combined with any collision avoidance algorithm that produces a field of vectors. In
particular, it is appropriate for artificial potential field methods. At the end of the paper, the presented
methodology is combined with an artificial potential fields algorithm recently proposed, the Potential Field
Projection method (PFP). This method is based on the combination of the classical Potential Fields method
and the multi-rate Kalman filter estimation and takes into account the uncertainties on locations, the future
trajectory of the robot and the obstacles and the multi-rate information supplied by sensors. As shown in the
simulation results, flexible trajectories for collision avoidance are generated with smooth curves.
1 INTRODUCTION
A robot can be defined as a machine that should be
able to collect information as well as to interact in a
natural way with the surrounding environment. The
key idea is how to obtain a proper trajectory that
must be smooth and must interact with the
environment in order to guarantee that the path is
free of collisions in real-time.
Collision avoidance is one of the main goals in
the research carried out in industrial applications. In
this sense, parametric curves are an option to
represent these trajectories. The properties of
parametric curves produce smooth paths. The most
commonly used in robotics are B-Splines, see for
instance (Connors and Elkaim, 2007), NURBS,
(Alleoti and Caselli, 2005), RBC, (Montes et al.,
2008) and Bézier.
The main difference between them is the
complexity of their mathematical definition. While
Bézier curves are the simplest ones, B-Splines or
NURBS are more complex although they can more
accurately represent objects in CAD programs.
However, in mobile robotics real-time applications
are required and, for this reason, more researchers
work with Bézier curves.
Moreover, (Nagatani et. al, 2001) used a path
planning algorithm based on Bézier curves
considering the minimum radius of curvature of
vehicle. (Hwang et. al, 2003) presented a new
interfacing method using a touchpad/screen to
control a mobile robot, capable of real-time dynamic
obstacle avoidance as well. They developed two
algorithms: a significant points extraction algorithm
for noisy input data and an on-line piecewise cubic
Bézier curves trajectory generation algorithm for a
mobile robot. (Skrjanc and Klancar, 2007)
developed a new cooperative collision avoidance
method for multiple nonholonomic robots with
constraints and known start and goal velocities based
on Bernstein-Bézier curves. The minimization
problem used is an inequality optimization problem.
The objective function minimizes the sum of all
absolute maximal times subjected to the distances
between the robots. (Choi et. al, 2008-2009)
presented two path planning algorithms based on
243
Hilario L., Montés N., Mora M. and Falcó A..
REAL-TIME TRAJECTORY MODIFICATION BASED ON BÉZIER SHAPE DEFORMATION .
DOI: 10.5220/0003086002430248
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 243-248
ISBN: 978-989-8425-31-7
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

Bézier curves for autonomous vehicles with
waypoints and corridor constraints. In this paper a
mathematical problem of constraint optimization is
used. The cost function is the curvature of the Bézier
curve to obtain resulting paths with larger radii of
curvature. (Lizarraga and Elklaim, 2008) used
Bézier curves for generating spatially deconflicted
paths for multiple UAVs (unmanned aerial vehicles).
The critical issue addressed is that of guaranteeing
that all the paths lie inside a predefined airspace
volume. Bézier curves represent a natural tool for
meeting this requirement (convex hull’s property).
The path generation problem is formulated as a
constrained optimization problem over a finite
optimization set and solved using standard
MATLAB optimization tools. In this case, the cost
function penalizes excessive lengths; the vehicles
must use the shortest possible path. The constraint of
the problem is the distance between the multiple
vehicles, as the generated paths must have a
minimum separation among them. The problem is
non-linear and the solution is obtained by numerical
techniques.
Through these works we can conclude that an
ideal solution is having a mathematical tool to obtain
the deformation of the predefined trajectory,
obtaining the modified curve in real time. In the
literature, there is a similar research topic where all
of the customary parametric curves are used, see
(Meek et. al, 2003) for NURBS shape modification
and (Fowler and Bartels, 1993) for B-Spline shape
modification.
In (Xu et. al, 2002) the Bézier shape
modification by constrained optimization based on
the discrete coefficient norm is discussed. The
problem of parametric curves shape modification by
constrained optimization was proposed recently.
(Wu and Xia, 2005) developed a new technique to
modify a Bézier curve by minimizing the changes of
the shape. This result was used by (Montés et. al,
2008) and it was improved and developed for Liquid
Composite Moulding Processes. This is our previous
work, defined as Bézier Shape Deformation (BSD).
This method computes the modification of the shape
defining a constraint optimization problem solved by
the Lagrange Multipliers theorem. In this theorem a
cost function is defined to minimize the distance
between two curves and a set of constraints are used
to obtain our aim. The principal constraint is how
the modified curve passes through the “Target
Point”. The rest of constraints are necessary to
obtain a smooth curve, for example, continuity and
derivability on the full curve.The advantage of this
method is the possibility to add as many different
constraints as necessary to obtain the best solution.
The current paper proposes a new path planning
algorithm that has the ability to interact with the
environment. This fact is able due to the
combination of a proposed mathematical tool, called
BSD, and an algorithm that gives repulsive forces.
In the present work we use a very recent work in this
field, (Mora et al., 2007).
This paper is organized as follows: Section 2
defines the Bézier curve and its useful properties for
path planning. Section 3 develops the new technique
called Bézier Shape Deformation (BSD). In Section
4, simulation results are given. Finally, Section 5
provides the conclusions and future work.
2 DEFINITIONS AND
PRELIMINARY NOTATION
The Bézier curve of degree n, given (n+1) control
points,
i
P , is defined to be
() ()
[]
,
0
;0,1
n
iin
i
tBtt
=
=⋅ ∈
∑
α P
(1)
where t is a normalized time variable, 0≤ t/T
max
≤1,
and
(
)
,ni
B
t
, are called the Bernstein polynomials or
Bernstein Basis functions of degree n.
()
()
⎪
⎩
⎪
⎨
⎧
≤≤−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
otherwise ,0
0;1
,
nitt
i
n
tB
i
in
ni
(2)
Bézier curves have useful properties for path
planning because: always pass through the first and
the last control points, lie within the convex hull of
the control points, they are tangent to the vector of
the difference P
1
-P
0
at the start point and the vector
of the difference P
n
-P
n-1
, they can be translated and
rotated by performing these properties on the control
points and in any case a smooth curve is guaranteed.
The displacement of every control point is denoted
as:
[
]
n
εεε 
0
=
. The Bézier curve obtained
modifying its controls points,
()
()
St
ε
α
, is defined to
be
()
,
0
(): ( ) ()
n
ii ni
i
tBt
=
=+⋅
∑
ε
S α P ε
(3)
ICEC 2010 - International Conference on Evolutionary Computation
244

3 BÉZIER SHAPE
DEFORMATION IN MOBILE
ROBOTS AND OBSTACLES.
To deform a given Bézier curve, we only need to
change the control points, and then it is necessary to
compute the perturbation
i
ε
of every control point.
For that, a constraint optimization problem is
proposed. Then, it is necessary to define a cost
function to optimize and a set of constraints to
obtain the desirable solution.
The cost function to optimize is defined as
follows;
()()() ()
()
∫
∑
∫
∑
∫
⎟
⎠
⎞
⎜
⎝
⎛
⋅=
=⋅=−
=
=
1
0
2
0
,
1
0
2
2
0
,
1
0
2
2
min
minmin
dttB
dttBdtttS
n
i
ini
n
i
ini
ε
εαα
ε
ε
ε
ε
(4)
This function minimizes the changes of the shape
minimizing the distance between both curves (see
Figure 1).
Figure 1: The deformation of a Bézier curve.
A Bézier curve constructed using a large number
of control points is numerically unstable (Skrjanc
and Klancar, 2007). For this undesirable property it
is necessary to concatenate two or more Bézier
curves of second order to represent the full trajectory
joining the initial and final positions of the mobile
robot. The order of the Bézier curve must not be
third or higher because it produces a loop or a cusp
depending of the geometrical location of the control
points.
()
()
()
() ()
()
∑
∫
∑
∫
∑∑
====
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=⋅
k
l
n
i
in
l
i
k
l
n
i
in
l
dttBdttB
l
l
k
i
k
1
1
0
2
0
,
)(
,,
1
0
1
2
2
0
,
)(
1
1
minmin εε
εεεε 
(5)
Our goal is to develop a navigation algorithm
that satisfies a set of constraints:
1.-The modified Bézier curve
()
()
α t
ε
S
passes
through the target point T. Thus, the curve satisfies
the following constraint:
() ()
(
)
(
)
(
)()
(
)
(
)
0,,0
11
=−=−
l
kl
l
k
l
l
l
tStS αTαT
εε

(6)
2.-To maintain the derivative property of the curve,
derivative restrictions in the start and end points of
the resulting concatenated curve are imposed to the
constrained optimization method,
(
)
(
)
(
)
() ()
(
)
0000
1
0
1
11
'
1
'
1
=−⋅⇒=− εεαSα
ε
n
,
(
)
(
)
(
)
() ()
(
)
0011'
1
'
1
=−⋅⇒=−
−
k
n
k
nkk
kk
n εεαSα
ε
(7)
3.- Continuity has to be imposed in the joined points
of the concatenated curves,
()
()
()
()
()
()
()
() 001,,001
1221
=−=−
−− kk
αSαSαSαS
εεεε

(8)
The evaluation of these equations is,
(
)
(
)
(
)
(
)
()
(
)
() () 1
0
1
01
0,,1
++
+
+=+=
ll
l
l
n
l
nl
ll
εpαSεpαS
εε

(9)
4.- Derivability is also required,
() () () () () () () ()
001,,001
'
1
'
2
'
2
'
1
=−=−
−− kk
αSαSαSαS
εεεε

(10)
(
)
(
)
(
)
(
)
(
)
() ()
(
)
[
]
l
n
l
n
l
n
l
nll
llll
n
11
'
1
−−
−+−⋅= εεppαS
ε
(
)
(
)
(
)
(
)
(
)
() ()
(
)
[
]
1
0
1
1
1
0
1
11
'
1
0
++++
++
−+−⋅=
llll
ll
n εεppαS
ε
(11)
The Lagrange multipliers theorem is applied to solve
the constrained optimization problem. The
constraints are added to the cost function resulting in
the Lagrange function defined as,
(
)
43211
rrrrgL
i
++
+
+
=
ε
(12)
The cost function is:
()
()
dttBg
k
l
n
i
in
l
i
l
2
2
1
0
10
,1
∫
∑∑
==
= ε
(13)
The constraints are included in the Lagrange
function as follows,
() ()
()()
∑∑
==
−=
k
l
r
j
l
jl
l
j
l
tr
11
1
, αSTλ
ε
(14)
(
)
(
)
(
)
(
)
(
)
() 11,00,
'''
1
'
12 kk
r αSαλαSαλ
εε
−+−=
(15)
()
()
()
()
1
31
1
,1 0
k
ll
l
r
−
+
=
=−
∑
εε
λ S α S α
(16)
()
()
()
()
1
41
1
,'1 '0
k
ll
l
r
−
+
=
=−
∑
εε
λ S α S α
(17)
This function depends on these variables,
REAL-TIME TRAJECTORY MODIFICATION BASED ON BÉZIER SHAPE DEFORMATION
245

()
(
)
(
)
λεε ,,,
1 k
LL …=
(18)
The number of the constraints depends on the
number of the concatenated Bézier curves,
()() 1111
1
−+−+++
∑
=
kkr
k
l
l
(19)
The problem is solved making zero the partial
derivatives of the Lagrange function,
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
∂
∂
=
∂
∂
0
0
λ
ε
L
L
l
(20)
In this way, a system of linear equations is obtained,
⋅=AX b
The characteristics of this system are:
1.- The variable vector is a column vector,
(
)
()
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
λ
ε
ε
X
k

1
(21)
2.- The independent vector is a column vector too,
[
]
C0vv0b ,,,
)()1( kT
=
(22)
The terms of b
T
are defined as,
(
)
(
)
[
]
)()()(
1
)(
1
)( l
r
l
r
lll
ll
STSTv −−= 
(23)
() () ( ) ( )
[
]
1,,11,,01,2,11,2,0
,,,,
−−
=
kkkk
CCCCC 
(24)
()()
(
)() 1
01,,0
−
−
−=
l
n
l
ll
l
ppC
()()
()
(
)
(
)
() ()
(
)
ll
l
l
n
l
nlll
nn
ll
01
11
111,,1
1
ppppC −⋅+−⋅=
−−
−−−
−
(25)
3.- The matrix of the system is defined in (26). It is a
square matrix defined as a block matrix. Every block
is defined as a part of the cost function or the
constraints. This form allows adding new blocks that
belong to other constraints.
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
000A
000A
000A
AAAA
A
41
31
21
14131211
(26)
The solution of this system is obtained as,
bAX
1−
=
(27)
The most important advantage of the proposed
method is that the solution is not an approximation.
It is an accurate solution. Another important thing is
its low computational cost. The deformation of the
initial robot path can be done in real time because
the problem to solve is linear and the inverse matrix
A
-1
can be computed in advance.
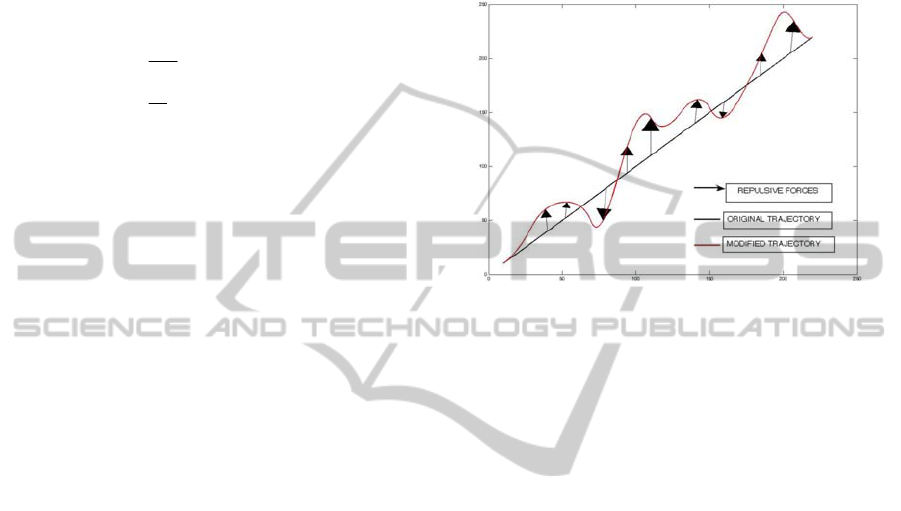
In Figure 2 it is shown a numerical result of the
BSD algorithm. The modified trajectory is computed
in 0.23 ms in a Pentium IV 2.4 Ghz.
Figure 2: Numerical Result of the BSD with ten Bézier
curves of second order.
4 SIMULATION RESULTS
The technique explained above has been evaluated
through a predictive path planning method described
in (Mora et. al, 2007) and (Mora and Tornero, 2007),
the Potential Field Projection method (PFP). This
method is based on the combination of the classical
Potential Fields method (Khatib, 1986) and the
multi-rate Kalman filter estimation (Tornero et. al.,
1999), (Pizá, 2003) and takes into account the
uncertainties on locations, the future trajectory of the
robot and the obstacles and the multi-rate
information supplied by sensors.
Dynamic models of moving objects are essential
in the estimation procedure. In this case, particle
kinematic models, described in (Mora et. al, 2007),
have been used for the robot and the obstacles.
Predicted future positions and uncertainties are
obtained from the prediction equations of the multi-
rate Kalman filter (28) for every object in the
environment, where
ˆ
x
∈ℜ
n
is the state estimation
vector, A∈ℜ
nxn
, B∈ℜ
nxm
and C∈ℜ
pxn
are the state
space matrices for linear systems, P∈ℜ
nxn
is the
error estimation variance matrix, K∈ℜ
nxp
is the
Kalman gain and Q∈ℜ
nxn
and R ∈ℜ
pxn
are,
respectively, the process noise and the measurement
noise covariance matrices.
ICEC 2010 - International Conference on Evolutionary Computation
246

[]
1/ /
T
1/ /
1
TT
/1 /1
//1 /1
//1 /1
ˆˆ
ˆˆ ˆ
kk kk k
kk kk
kkk kk k
kk kk k k kk
kk kk k kk
+
+
−
−−
−−
−−
=⋅ +⋅
=⋅ ⋅ +
⎡⎤
=⋅⋅⋅⋅+⋅
⎣⎦
=+⋅−⋅
=−⋅⋅
xAxBu
PAPAQ
KP CCP CR Δ
xx KzCx
PP KCP
(28)
The delta function Δ modifies the expression of
the Kalman gain indicating the presence (unit Δ
matrix) or the absence (zero Δ matrix) of
measurements in one particular estimation instant.
Predicted future positions are derived imposing zero
Δ matrices for future instants, as measurements are
not available.
Regarding to the robot, the sequence of predicted
positions is considered as the Start points, S
i
, of the
reference trajectory for the Bézier Shape
Deformation method explained above. Every Start
point is located in each second order Bézier curve.
Regarding to the obstacles, their future trajectories
and associated uncertainties are considering as
restricted areas for path planning.
These predicted trajectories are used in the
generation of the potential field U(q,i)=U
att
(q,i)+
U
rep
(q,i), defined in (Mora et. al., 2007) even in the
instants of time without measurements of the
environment (i>0).
The potential field generates a force in every
prediction instant i, F(q,i)=-∇U(q,i), that modifies
the initial prediction depending on the location of
the goal and the future trajectories of the obstacles.
In fact, these set of forces are transformed into
displacements taking into account a particle dynamic
model. These displacements are the Target points,
T
i
, defining the necessary vector, v, for the BSD.
With the BSD algorithm we are able to compute
a new Bézier curve in real-time that modifies the
preliminary predicted trajectory. This new curve
guarantees the smoothness and the continuity.
A simulation application has been implemented
in Matlab in order to demonstrate the statements
above. Figure 3 represents a 2D four-sided scenario
with six mobile obstacles and a mobile robot. The
uncertainty ellipses associated to each predicted
position within the prediction horizon are also
depicted for the robot (in red) and the obstacles (in
pink). Initially, the robot and the obstacles follow
linear trajectories (given by the kinematic model)
going from side to side of the environment.
When the obstacles come close to the robot, it
starts a smooth avoiding manoeuvre, based on the
Bézier Shape Deformation method, which modifies
its initial trajectory and guides the robot to the goal
without collision. In Figure 3a the robot is following
a straight line trajectory when a future collision is
detected. The initial trajectory is modified in real-
time using the BSD method and the resulting
trajectory is shown in Figure 3b and Figure 3c.
Finally, Figure 3d shows another avoidance
manoeuvre the modified trajectory.
5 CONCLUSIONS AND FUTURE
WORK
This paper presents a new technique, called Bézier
Shape Deformation (BSD), for a flexible path
planning based on the deformation of a Bézier curve
through vectors. These parametric curves represent
in a proper way an optimized path satisfying a set of
constraints at the same time. The main advantage of
this method is the solution obtained; it is an accurate
solution of a linear system and the computational
cost is low. It computes a new trajectory in real-time
avoiding the obstacles in the environment. These
obstacles generate repulsive forces; these vectors are
introduced in the BSD algorithm. The method used
to solve it is the Lagrange theorem. The simulation
results show the successful resulting trajectory.
a) b) c) d)
Figure 3: Simulation application - A robot follows a straight line avoiding the mobile obstacles using the BSD method.
REAL-TIME TRAJECTORY MODIFICATION BASED ON BÉZIER SHAPE DEFORMATION
247

Future work lines are: the problem definition can
add as many constraints as necessary. The matrix is
defined with blocks, and it implies only to change or
to include a new block in the matrix. It is important
to work with the curvature or the total length of the
path because in a vehicle robot there is a maximum
curvature that the vehicle can follow and the path
length affects the total travel time. Both functions
could be including in the definition problem as a
cost function or as a constraint.
Finally, another future research is how to extend
it to 3D space. In this way, the trajectory of an UAV
or a robot arm could be simulated.
ACKNOWLEDGEMENTS
This research work is financially supported by the
project GV/2010/054 of the Generalitat Valenciana.
REFERENCES
Aleotti, J., Caselli, S., 2005. Trajectory Clustering and
Stochastic Approximation for Robot Programming by
Demonstration. In IROS 2005, IEEE Int. Conf. On
Intelligent Robots and Systems, pp. 1029 - 1034.
Aleotti, J., Caselli, S., 2005. Trajectory Reconstruction with
NURBS Curves for Robot Programming by
Demostration. In CIRA 2005, IEEE Int. Symp. on
Computational Intelligence in Robotics and
Automation, pp. 73-78.
Choi, J., Elkaim, G. 2008. Bézier Curves for Trajectory
Guidance. In WCECS 2008, World Congress on
Engineering and Computer Science, pp. 625-630.
Choi, J., Curry, R., Elkaim, G., 2008. Path Planning based
on Bézier Curve for Autonomous Ground Vehicles. In
WCECS 2008, World Congress on Engineering and
Computer Science, pp. 158 - 166
Choi, J., Curry, R., Elkaim, G. 2009. Smooth Path
Generation Based on Bézier Curves for Autonomous
Vehicles. In WCECS 2009, World Congress on
Engineering & Computer Science Vol II, pp.668-673.
Connors, J., Elkaim, G. 2007. Analysis of a Spline Based,
Obstacle Avoiding Path Planning Algorithm. In
VTC2007, IEEE Vehicle Technology Conference, pp.
2565-2569
Fowler, B., Bartels, R., 1993. Constrained-based curve
manipulation. IEEE Computer Graphics and
Applications 13, 5, pp. 43-49.
Hwang, J. H., Arkin, R. C., Kwon, D. S., 2003. Mobile
Robots at your fingertip: Bézier curve on-line trajectory
generation for supervisory control. In IROS 2003, Int.
Conf. on Int. Robots and Systems, pp.1444-1449.
Khatib, O., 1986. Real-time obstacle avoidance for
manipulators and mobile robots. In The International
Journal of Robotics Research, 5, 1, pp. 90-98.
Lizarraga, M., Elklaim, G., 2008. Spatially Deconflicted
Path Generation for Multiple UAVs in a Bounded
Airspace. In PLANS 2008, ION/IEEE Position,
Location and Navigation Symposium, pp. 1213 - 1218.
Meek, D. S., Ong, B. H., Walton, D. J., 2003. Constrained
interpolation with rational cubics. In Computer Aided
Geometric Design 20, pp. 253-275.
Montés, N., Sánchez, F., Hilario, L., Falcó, A. 2008. Flow
Numerical Computation through Bézier Shape
Deformation for LCM process simulation methods. In
Int. Journal of Material Forming, 1, pp. 919-922.
Montés, N., Herráez, A., Armesto, L., Tornero, J., 2008.
Real-time clothoid approximation by Rational Bézier
curves. In ICRA 2008, IEEE Int. Conf. on Robotics
and Automation, pp.2246 – 2251.
Mora, M. C., Pizá, R., Tornero, J., 2007. Multirate obstacle
tracking and path planning for intelligent vehicles. In
IV’07, IEEE Int.Vehicles Symposium, pp. 172-177.
Mora, M. C., Tornero, J., 2007. Planificación de
movimientos mediante la propagación de campos
potenciales artificiales. In CIBIM8, 8º Congreso
Iberoamericano de Ingeniería Mecánica, e-book.
Nagatani, K., Iwai, Y., Tanaka, Y., 2001. Sensor Based
Navigation for car-like mobile robots using Generalized
Voronoi Graph. In IROS 2001, Int. Conf. on Intelligent
Robots and Systems, pp. 1017-1022.
Pizá, R., 2003. Modelado del entorno y localización de
robots móviles autónomos mediante técnicas de
muestreo no convencional, PhD Thesis, Universidad
Politécnica de Valencia, Valencia.
Wu, Q. B., Xia, F. H., 2005. Shape modification of Bézier
curves by constrained optimization. In Journal of
Zhejiang University-Science A, pp 124-127.
Skrjanc, I., Klancar, G., 2007. Cooperative Collision
Avoidance between Multiple Robots Based on Bézier
Curves.In ITI 2007, 29
th
Int. Conf. on Information
Technology Interfaces, pp. 451-456.
Tornero, J., Salt, J., Albertos, P., 1999. LQ Optimal
Control for Multirate Sampled Data Systems. In 14
th
IFAC World Congress, pp. 211-216.
Xu, L., Chen, Y. J., Hu, N., 2002. Shape modification of
Bézier curves by constrined optimization. In Journal
of software (china), 13, 6, pp. 1069-1074.
ICEC 2010 - International Conference on Evolutionary Computation
248