
A GENETIC ALGORITHM WITH A MULTI-LAYERED
GENOTYPE-PHENOTYPE MAPPING
Seamus Hill and Colm O’Riordan
Computational Intelligence Research Group, National University of Ireland, Galway, Ireland
Keywords:
Genetic algorithms, Genotype, Phenotype, Deception.
Abstract:
In this paper we investigate the introduction of a multiple-layer genotype-phenotype mapping to a Genetic
Algorithm (GA) which attempts to mimic more closely, the effects of nature. The motivation for introducing
multiple-layers into the genotype-phenotype mapping is to create a many-to-one genotype-phenotype mapping.
The paper compares a traditional GA with a GA containing a multi-layered genotype-phenotype mapping using
a number of well understood problems in an attempt to illustrate the potential benefits of including the multi-
layered mapping. Initial findings suggest that the multi-layered mapping between the genotype-phenotype
used in conjunction with a binary representation outperforms existing traditional GA approaches on well
known problems, while still allowing the use well understood genetic operators.
1 INTRODUCTION
Genetic Algorithms (GAs) (Holland, 1975) are search
algorithms based on the mechanics of natural selec-
tion and natural genetics and are a often used to solve
complex optimisation problems. However in nature
there exists a intermediate layer between the genotype
and the phenotype, which differs from the mapping
found in a traditional GA. By introducing multiple-
layers, which attempts to mimic more closely the ef-
fects of nature, into the genotype-phenotype mapping
we aim to and to maintain diversity in the popula-
tion and introduce a many-to-one genotype-phenotype
mapping. The paper compares a GA with a multi-
layered genotype-phenotype mapping to a traditional
GA using a number of well understood problems us-
ing different levels of deception in an attempt to create
a proof of concept. The paper is organised as follows:
section 2, a review of a selection of previous work.
Section 3 outlines the multiple mapping GA proposed
by the authors. Section 4 describes the experiments
conduced, while section 5 discusses the findings. Fi-
nally, section 6 concludes and outlines future work.
2 BACKGROUND
The motivation for attempting to create a GA which
includes a number of biologically plausible concepts
and yet provides a framework based on a binary
string, stems from the desire to allow a GA to provide
a many-to-one representation and to test how tradi-
tional GA operators operate within this environment.
Another motivation is that for a simple GA, solving
deceptive problems can be difficult because of pre-
mature convergence. By using intermediate layers in
the genotype space, it is hoped to is to overcome this
failing while still using a binary representation.
3 MULTI-LAYERED MAPPING
GENETIC ALGORITHM
(MMGA)
The mmGA operates using a binary representation
which allows the use or standard genetic operators
such as crossover and mutation. The difference be-
tween the multi-layered mapping GA (mmGA) and
the standard representation found in a GA lies in the
fact that it contains multiple layers of mappings be-
tween the genotype to the phenotype. To discuss the
mapping, consider the collections of genes 11100001,
11101100, 10110001 and 11000110. The mmGA
randomly creates the genome string and the strings
are converted to a DNA template using the follow-
ing mapping 00 → A; 01 → C; 10 → G and 11 → T.
This maps the strings 11100001 → TGAC; 11101100
→ TGTA; 10110001 → GTAC and 11000110 → TACG.
The next step in the mmGA mapping is a conversion
369
Hill S. and O’Riordan C..
A GENETIC ALGORITHM WITH A MULTI-LAYERED GENOTYPE-PHENOTYPE MAPPING.
DOI: 10.5220/0003086203690372
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 369-372
ISBN: 978-989-8425-31-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

from the template to DNA coding using the mapping
G → C; A → T ; T → A and C → G. The templates
TGAC becomes ACTG, TGTA becomes ACAT, GTAC be-
comes CATG and TACG maps to ATGC.
The final stage of transcription are now carried
out and the DNA coding strings are now converted
into RNA where the only change maps T → U . The
final stage of transcription are now carried out and
the DNA coding strings are now converted into RNA.
The strings ACTG, ACAT, CATG and ATGC now become
the proteins ACUG, ACAU, CAUG and AUGC respectively.
These proteins are in turn then converted into traits
i.e. 0 or 1 based upon the mapping generated by the
mmGA, which are then combined to create the pheno-
type. The mappings created by the mmGA allow for
a many-to-one relationship between the genotype and
the phenotype. The mapping can be summarised as
follows; 11100001 → T GAC → ACT G → ACUG →
0; 11101100 → T GTA → ACAT → ACAU → 1;
10110001 → GTAC → CAT G → CAU G → 0 and
11000110 → TACG → ATGC → AU GC → 1. The
pseudocode for the process is outlined in Algorithm
1.
Algorithm 1: Pseudecode - multi-layered map-
ping Genetic Algorithm.
initialize mmGA;
r=1; (Number of runs);
for Number of runs do
Initialise Individual Genomes P(g);
Transcribe Genome to Amino Acids P(g);
Translate Amino Acids to Phenotype P(g);
Evaluate P(g); (Phenotype fitness);
for Number of Generations do
g=0; (generations);
for All members of P do
Select P(g) from P(g-1);
Crossover P(g); genotype level;
Mutation P(g); genotype level;
Transcribe Genome to Amino
Acids P(g);
Translate Amino Acids to
Phenotype P(g);
Evaluate P(g); (phenotype fitness);
end
g+=1;
end
r+=1;
end
end mmGA;
4 EXPERIMENTS
In this paper the authors choose four types of problem
to examine the effects of extending the representation;
a two-bit minimal deceptive problem, a three-bit fully
deceptive problem, a 100-bit One Max problem and a
fully deceptive 30 bit problem.
4.1 Minimal Deceptive Problem (MDP)
A problem which causes a GA to diverge from the
global optimum. can be viewed as a deceptive prob-
lem. By using short low-order building block to lead
the search away from the global optimal to a sub-
optimal point in the search space we are deceiving
the GA. The MDF exhibits the characteristics of a
epistatic problem and as it can be shown that one-bit
problems cannot be deceptive the MDP is the smallest
deceptive problem possible and by using a MDP one
can carry out analysis into the workings of GAs.
4.2 Three Bit Fully Deceptive Problem
A fully deceptive problem of order-N can be viewed
as being deceptive when all of the lower-order hyper-
planes lead away from the global optimum and to-
wards a deceptive attractor (Whitley, 1991). We use a
fully deceptive order-3 problem as outlined by (Gold-
berg et al., 1990) in this paper.
4.3 One-max Problem
The One-Max problem (Ackley, 1987) can
be described formally as having a string
¯x = {x
1
, x
2
, . . . , x
N
}, with x
i
∈ {0, 1}, which at-
tempts to maximise the following:
f (¯x) =
N
∑
i=1
x
i
In this paper the authors have defined N = 100.
4.4 Thirty-bit Fully Deceptive Problem
One failing of the 3-bit fully deceptive problem is that
it is too small to really demonstrate a search strategy.
The thirty-bit problem as outlined in (Goldberg et al.,
1990) expands the three-bit problem into ten three-bit
deceptive order-three subfunctions. To increase the
level of difficulty we include a loose ordering, which
makes the problem fully deceptive. This is achieved
by increasing the defining length to twenty, where the
defining length is the maximum distance between two
defining symbols in a schema.
ICEC 2010 - International Conference on Evolutionary Computation
370
5 FINDINGS
We compare both the traditional GA and the mmGA
over a suite of problems containing a two-bit minimal
deceptive problem, a three-bit fully deceptive prob-
lem, a one hundred-bit One-Max problem and a fully
deceptive thirty-bit problem. For the first three prob-
lems, each set of experiments has a population size of
one hundred and is executed for two hundred genera-
tions. For the final problem, the thirty-bit fully decep-
tive the population size was increased to two hundred
and the algorithm run for three thousand generations.
Each experiment is executed over one hundred runs.
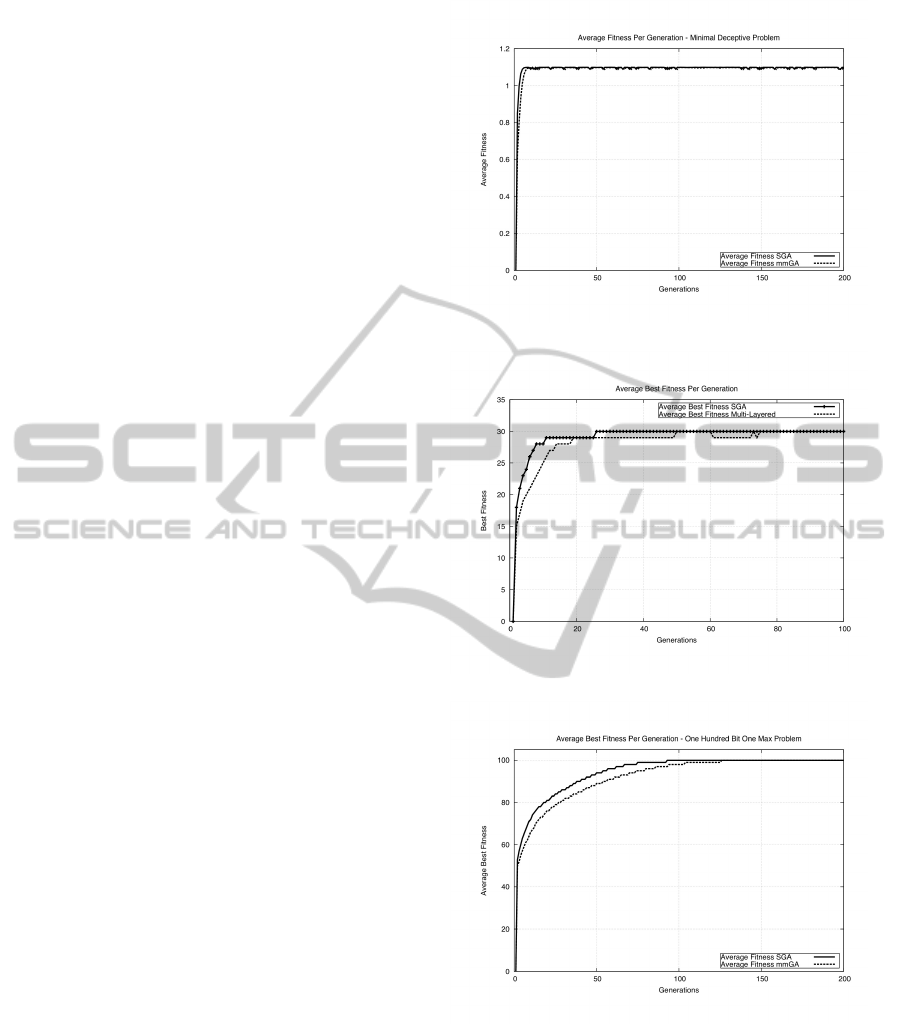
Figure 1 illustrates that the performance of the
mmGA compares with that of a traditional GA., pos-
sibly because the MDP problem is easy for both forms
of a GA to solve. Which may indicate that there is lit-
tle to be gained by adopting the more complex multi-
layered GA on easy problems. Figure 2 shows the
performance of both GAs on a three-bit fully decep-
tive problem, which is considered GA hard. Although
both GAs are successful in locating the global opti-
mum, the GA using a traditional representation con-
verges on the global optimum, while the mmGA con-
verges for a number of generations but due to the
multi-layered representation and many-to-one repre-
sentation continues to explore the search space.
When comparing the results in Figure 2 to those of
Figure 1, we see that although both forms of GA con-
verge on the global optimum, it appears that the more
difficult landscapes offer the GAs a more challenging
task and that there may be an advantage in using a
multi-layered mapping particularly on difficult prob-
lems. In Figure 3 we see the performance of both
GAs on the One-Max problem. However, the One-
Max problem can be viewed as a landscape that is rel-
atively easy for a GA to search. The results indicate
that both forms of a GA were successful at converg-
ing on the global optimum. The standard GA appears
to have located the global optimum in a shorter time
frame than the mmGA. The authors believe that the
reason for this is due to the difference in the genotype-
phenotype mapping and that the extra time take for
the mmGA relates to the increased search space. This
we believe should not be viewed negatively as it re-
duces the prospect of premature convergence for the
mmGA.
The thirty-bit fully deceptive problem makes the
problem far more difficult to solve particularly as the
defining length has increased. Figure 4 show that the
average fitness level per generation for the traditional
GA is higher than that of the mmGA, as the tradi-
tional GA has converged prematurely on the decep-
tive attractor. However, figure 5 shows the average
Figure 1: Two-bit minimal deceptive problem - Average fit-
ness per generation.
Figure 2: Fully deceptive problem - Average best fitness per
generation.
Figure 3: One hundred bit one max problem - Average best
fitness per generation.
best fitness per generation and results show that the
SGA failed to locate the global optimum as it con-
verged on the deceptive attractor. The mmGA how-
ever, did manage to locate the optimum. This ap-
pears to indicate that the genotype-phenotype map-
ping contained in the mmGA exhibits the ability to
avoid premature convergence and continue the search
to locate the global optimum. Figure 6 allows us to
see the number of subfunctions discovered per gen-
A GENETIC ALGORITHM WITH A MULTI-LAYERED GENOTYPE-PHENOTYPE MAPPING
371

Figure 4: Thirty-bit fully deceptive problem - Average fit-
ness per generation.
eration. We can see from the plot that mmGA out-
performs the traditional GA in locating the ten fully
deceptive subfunctions.
Figure 5: Thirty-bit fully deceptive problem - Average best
fitness generation.
Figure 6: Thirty-bit fully deceptive problem - Sub functions
discovered 3000 generations.
6 CONCLUSIONS
Initial results indicate that the mmGA has the abil-
ity to solve a number of problems over varying fit-
ness landscapes. By introducing a multi-layered re-
lationship between the genotype and the phenotype,
the mmGA offers the ability to introduce a many-to-
one genotype-phenotype mapping. This implies that
identical phenotypes may be created from different
genomes. From the results outlined above, it appears
that the extended genotype-phenotype representation
exhibits the ability to avoid premature convergence,
particularly on more difficult problems.
REFERENCES
Ackley, D. H. (1987). A connectionist machine for genetic
hillclimbing. Kluwer Academic Publishers, Norwell,
MA, USA.
Goldberg, D. E., Korb, B., and Deb, K. (1990). Messy
genetic algorithms: Motivation, analysis, and first re-
sults. Complex Systems, 3(5):493–530.
Holland, J. H. (1975). Adaptation in natural artificial sys-
tems. University of Michigan Press, Ann Arbor.
Whitley, L. D. (1991). Fundamental principles of deception
in genetic search. In Rawlins, G. J., editor, Founda-
tions of genetic algorithms, pages 221–241. Morgan
Kaufmann, San Mateo, CA.
ICEC 2010 - International Conference on Evolutionary Computation
372
