PROTEIN SECONDARY STRUCTURE PREDICTION USING

KNOWLEDGE-BASED POTENTIALS

Saras Saraswathi, Robert L. Jernigan, Andrzej Kloczkowski

Department of Biochemistry, Biophysics and Molecular Biology

L.H. Baker Center for Bioinformatics and Biological Statistics

112 Office and Laboratory Building, Ames, IA, 50011, U.S.A.

Andrzej Kolinski

Laboratory of Theory of Biopolymers, Faculty of Chemistry, Warsaw University, Pasteura 1, 02-093 Warsaw, Poland

Keywords: Protein secondary structure prediction, Neural networks, Extreme learning machine, Particle swarm

optimization.

Abstract: A novel method is proposed for predicting protein secondary structure using data derived from knowledge

based potentials and Neural Networks. Potential energies for amino acid sequences in proteins are

calculated using protein structures. An Extreme Learning Machine classifier (ELM-PSO) is used to model

and predict protein secondary structures. Classifier performance is maximized using the Particle Swarm

Optimization algorithm. Preliminary results show improved results.

1 INTRODUCTION

Large scale advances in genome sequencing and

resultant availability of large numbers of proteins

sequences has given protein secondary structure

prediction increasing importance in computational

biology. Improvements in secondary structure

prediction can lead to progress in protein

engineering and drug design. Existing

crystallographic techniques are too expensive and

time consuming for large-scale determination of

protein three-dimensional structures. Prediction of

secondary structures might be a useful intermediate

step to speed up structure prediction (Lomize,

Pogozheva and Mosberg, 1999 and Ortiz, Kolinski,

Rotkiewicz, Ilkowski and J. Skolnick, 1999).

Secondary structure prediction can assist in gene

function and sequence annotation, as well as

identification and classification of structures and

functional motifs and in identifying malfunctioning

structures which cause human diseases.

Several computational methods have been

successfully used in secondary structure prediction,

of which empirical and machine learning methods

have proved to be the most successful. Chou and

Fasman (1974), Qian and Sejnowski (1988), Ward,

McGuffin, Buxton, and Jones (2003) were followed

by numerous others. The GOR method based on

information theory was used by Garnier,

Osguthorpe, and B. Robson, (1978) and later by

Garnier, Gibrat, and Robson (1996). Kloczkowski,

K.L. Ting, R.L. Jernigan, and J. Garnier (2002) used

evolutionary information in GOR V for improved

structure prediction. PredictProtein server (Rost, G.

Yachdav, and J. Liu, 2004) uses multiple sequence

alignment based neural networks. The PSIPRED

algorithm developed by Jones (1999) uses PSI-

BLAST (Altschul, T.L. Madden, A.A. Schäffer, J.

Zhang, Z. Zhang, W. Miller, and D.J. Lipman, 1997)

and neural networks. The Jpred prediction server

(Cole, Barber, and Barton, 2008), runs on the Jnet

algorithm (Cuff and Barton, 2000). Montgomerie,

Sundaraj, Gallin, and Wishart (2006) and Pollastri,

Martin, Mooney and Vullo, (2007) developed large

scale secondary structure prediction methods using

existing structural information and computational

methods to claim an accuracy of 90% for sequences

with over 30% sequence homology. Kihara (2005)

suggested that long-range interactions are an

important factor to be considered in order to achieve

higher classification accuracy.

370

Saraswathi S., Jernigan R., Kloczkowski A. and Kolinski A..

PROTEIN SECONDARY STRUCTURE PREDICTION USING KNOWLEDGE-BASED POTENTIALS.

DOI: 10.5220/0003086903700375

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages

370-375

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

We propose a novel strategy for secondary

structure prediction using knowledge based potential

profiles. A two stage Extreme Learning Machine

(ELM) (Huang, Q.Y. Zhu, and C.K. Siew, 2006)

classifier called the ELM-PSO is used for

classification of secondary structures. Performance

is improved using Particle Swarm Optimization

(PSO) (Clerc, J. kennedy, 2002).

This paper is organized as follows: Section 2

gives a brief description of the data. Section 3

describes the two-stage ELM-PSO classification

technique. Section 4 discusses the results and gives a

comparative study followed by conclusions in

Section 5.

2 DATA GENERATION USING

POTENTIAL ENERGY

The dictionary of secondary structure assignment

Database of Secondary Structure in Proteins (DSSP)

(Kabsch and Sander, 1983) has 8 classes of protein

secondary structures. We use only a reduced set of

three secondary structures, namely, alpha-helix (H),

beta-strand (E) and coil (C). Data is derived based

on CABS force-fields (Kolinski, 2004 – algorithm

for data generation has been submitted for

publication), which includes information pertaining

to long and short range interactions between amino

acids in proteins. A profile matrix was created using

the 513 non-homologous (target) protein sequences

from the CB513 data set (Cuff and Barton, 2000),

where the sequence homology is less than 30%.

3 METHODS

AND OPTIMIZATION

In a neural net framework, the input consists of a set

of patterns (residues), each having a set of 27

features (profile values), which are normalized to

values between 0 and 1. The output consists of three

units which correspond to one of three secondary

structure elements, represented as a 1 for the class of

interest and a -1 for the other two classes. A given

input is combined with a bias and a set of weights

and is processed through an activation function at

the hidden layer level. The output of the hidden

layer is combined with another set of weights to

yield three outputs. The predicted class is considered

as the output which has the maximum value, which

corresponds to choosing the output with the smallest

mean-squared error.

An Extreme Learning Machine (ELM) (

Huang,

Zhu, and Siew, 2006) classifier, which is a form of a

Neural Network, is used for classification. PSO

used to tune the parameters of the ELM. The data

was also evaluated using Support Vector Machine

(SVM) and Naïve Bayes (NB) algorithms using the

WEKA (

Witten and Frank,2005) software tool for

classification.

The profile data consists of 27 features for each

of N amino acids, where N is the number of residues

in a single protein. Of the 27 features, the first 9

features are the energy potentials related to alpha-

helices (H), the next 9 features are related to beta-

strands (E) and the last 9 features are related to coils

advantage in getting better classification accuracy,

since this information can be used during the

training phase (although this information will not be

available on a blind set or a new set of proteins).

Based on this prior knowledge, class specific

features of the target class can be given extra

weights (importance) compared to the rest of the

features that belong to the negative classes. Hence

the class specific features of each class (9 columns

per class) were scaled (values boosted) according to

a predetermined factor prior to building a training

model. These factors (not unique) were obtained by

brute force trial and error method, where selection

was based on getting better classification results. It

is noteworthy that the classification accuracy after

this scaling depends on the scaling factors used, and

ranges from 60% (for non-scaled data or data scaled

with sub-optimal boosting values), to over 95%,

when the optimal scaling factors are used. The first 9

features of all samples belonging to the H class,

were scaled by a factor of 5, while the second set of

9 features were scaled by a factor of 3 and the last

set of 9 features were scaled by a factor of 8. The

scaling of data improves the classification accuracy

considerably during the training phase. Samples

which were scaled according to their classes were

used for the 10-fold cross-validation in WEKA

(

Witten and Frank, 2005), which gave very high results for

SVM and Naïve Bayes algorithms. Since it is not

possible to perform class-specific feature scaling

during testing (blind) phase for the ELM method,

three sets of test samples were generated for each

sample in the test set. The first set had the first 9

features boosted in the same ratio as for the H class

for all samples. The second set of test samples had

the next set of 9 features boosted according to the

factor used for the E class for all samples and the

third set of test samples had the last set of 9 features

scaled according to the factor used for the C class

PROTEIN SECONDARY STRUCTURE PREDICTION USING KNOWLEDGE-BASED POTENTIALS

371

for all samples. Each test set was sent in turn and the

votes were collected for the classification. For

robustness, ten sets of training models were used to

get the classification results for the same test set.

Each training model yielded a set of three votes for

each sample. These votes were all gathered to

determine the class which receives the maximum

number of votes. The results for the classification

accuracies with and without feature scaling (value

boosting) are given in the results section. Blind

testing with voting was not done for SVM and Naïve

Bayes algorithms since it would require

modification of WEKA code.

Figure 1: Visualization of data without feature scaling.

Energy potentials are represented along the x-axis, the first

nine features belong to helix (H), the next 9 features are

for strand (E) and the last set of features 19 - 27 for coil

(C). The color intensity indicates the value of the potential

energy, with a dark blue for a low value and a red

indicates a high value. The residues (total: 4282) along the

y-axis have been sorted according to the three classes,

where residues 1 - 1487 belong to class H, 1488 - 2541

belong to class E and 2542 - 4282 belong to class C. Note:

there is not much horizontal differentiation among the

three classes which becomes evident in Fig. 2, after data is

subjected to feature specific scaling. Results for

classification of this unscaled data is given in Table 1.

3.1 Two Stage Extreme Learning

Machine

The ELM-PSO consists of the Extreme Learning

Machine (ELM) classifier as the main algorithm,

which uses a set of training samples to build a

model. During the training phase, PSO is called

upon to optimize the parameters, such as weights,

number of hidden neurons and bias of the ELM,

which results in improved classification accuracy.

These parameters are stored and used during the

testing phase. ELM is an improved version of a

feed-forward neural network consisting of a single

hidden layer. The initial set of input weights are

chosen randomly, but they are tuned later by the

PSO. The output weights from the hidden layer to

the output layer are analytically calculated, using a

pseudo inverse. A sigmoidal activation function is

used for the hidden layer and a linear activation

function is used for the output neurons. Huang,

Zhu

and Siew

(2006) give a comprehensive discussion of

ELM. The ELM algorithm consists of the following

steps:

1. Select the number of hidden neurons (H) and a

suitable activation function for a given problem.

2. Randomly choose the input weight (W) and bias

(b).

3. Analytically calculate the output weight using a

pseudo inverse which speeds up the traditional

neural network algorithm tremendously.

Store the calculated weights (W, b) and hidden

neurons (H) which yield the best training results.

Use these stored values for estimating the class

label during testing phase.

The estimated class label Ci is calculated using

equation (1) where

is the neural network output

for each class k, for sample i.

,..,2,1

maxarg



(1)

An improved version of the ELM algorithm

proposed by Saraswathi and Suresh et al., (2010),

shows that a random selection of initial parameters

(W, b, H) affects the performance of the ELM

classifier significantly. Tuning of input parameters

using PSO, improves classifier performance

considerably, by minimizing the error (Eq. 2), which

is the distance between the neural network output

(Y) and the target classes (T).







TYminargb,W,H

b,V,H

***



(2)

3.2 Particle Swarm Optimization

A stochastic optimization technique called Particle

Swarm Optimization (PSO) was developed by

Clerc

and Kennedy (2002).

This method mimics the

intelligent social behavior of flocks of birds or

schools of fish, represented as particles in a

population. These particles work together to find a

simple and optimal solution to a problem in the

shortest possible time. The PSO algorithm is

initialized with a set of random solutions called

particles. The algorithm iteratively searches a multi-

ICFC 2010 - International Conference on Fuzzy Computation

372

dimensional space for the best possible solution,

determined by a fitness criterion. PSO will find the

best combination of hidden neurons, input weights,

and bias values and return the (training) validation

efficiency obtained by the ELM algorithm along

with the best ELM parameters to obtain better

generalization performance. The best parameters

are stored and used during the testing phase.

4 RESULTS AND DISCUSSION

Several training models were built using ELM and

two other algorithms, namely SVM and Naïve Bayes

(NB) from the WEKA (

Witten and E. Frank, 2005) suit

of software for data classification. A 10-fold cross

validation was performed for SVM and NB, where

90% of the proteins were used to build the training

model while the remaining 10% were retained for

testing the model, but all input information was

scaled according to previously described values. A

blind test was conducted using ELM with 4797

proteins for training and 4835 for testing. These

residues were selected from a random selection of

30 proteins for the training set out of 400 proteins,

while the test samples came from a separate set of

41 proteins retained for testing. Preliminary studies

for the ELM-PSO classifier, SVM and NB show

high accuracies of around 99% for the scaled

training as seen in Table 2, while the results for the

unscaled version of the data, as seen in Table 1, is

much lower at only ~60% or less. The unscaled

version of the data uses only row specific feature

information while the scaled data also uses column

specific class information which increases the

accuracy considerably.

The lower testing accuracy of 94.4 % for the

ELM (blind) tested

4835 samples might be due to

the smaller number of residues tested as compared to

the other two models built from SVM and NB with

the full data set. The ELM classifier trains on sets of

2000 to 3000 samples at a time and builds several of

these models by selecting samples at random from

the pool of available training samples (from the 400

training proteins), a very computationally intensive

process. The parameters for every ELM model are

optimized by calling PSO and a single pattern from

the test set is repeatedly tested by each model,

giving a consensus classification for the type of the

test sample. The class that occurs with the highest

frequency in these classifications is taken to be the

predicted class for this test sample. Preliminary

results for a set of 4835 test samples are given in

Table1 and Table 2 for scaled and unscaled data.

On the other hand the high accuracies for SVM

and NB can be attributed to the technique of cross

validation where the input data is uniformly scaled

according to previous criteria, using feature specific

class information, which results in higher accuracy.

There is no blind test of data. So, unless the

algorithm can discern this feature specific pattern

automatically without involving the computationally

intensive ELM-PSO method that was used here, it is

not very practical. Future work will aim to improve

the ELM-PSO algorithm to learn this information

automatically.

Table 3 shows that the ELM-PSO methods

perform very well compared to other studies in the

literature for scaled data. The accuracy on the

unscaled data is lower for all models and is

comparatively low for the blind test, indicating that

the learning algorithm needs further tuning to

discern the column-wise information during (blind)

testing phase. The column-wise class information is

a unique feature of our data that separates the three

classes linearly and hence gives high results. Table1

and Table 2 also give the F-measure and area under

the curve (AUC) values for SVM and Naïve Bayes

classifications. These terms help us to gauge the

quality of the predictions.

Figure 2: Visualization of the same sample data shown in

Figure 1, given here with feature scaling. Descriptions of

the X,Y axes and colors are the same as given in Figure 1.

Compared to Figure 1, it can be seen that class-specific

feature scaling provides for a distinct separation of the

classes, which results in higher accuracy during

classification, using ELM, SVM-SMO and Naïve Bayes

algorithms, with results shown in Table 2.

The performance of classifications can be

evaluated in terms of the true positives (TP-correct)

and false positive (FP-error) terms. Similar

definition holds for true negatives (TN) and false

negatives (FN). The output of a classification might

provide estimated probabilities which determine the

predicted class according to a pre-set threshold. TP

rate and FP rate can be graphed as coordinate pairs

PROTEIN SECONDARY STRUCTURE PREDICTION USING KNOWLEDGE-BASED POTENTIALS

373

which form the receiver operating characteristic

curve (ROC curve).

The area under this ROC curve (AUC or

AUROC) helps to aggregate the performance of all

the testing results, where a higher value closer to

1.00 denotes perfect performance. F-measure gives

the test’s accuracy. It uses precision p and recall r of

the test, where p is the ratio of correct results divided

by all returned results (TP/(TP+FP)) and r is the

number of correct results divided by the number of

expected results (TP/(TP+FN)). F-measure is

calculated as given in equation (3), where the best

score for F-measure can be as high as 1 and the

worst score can be as low as 0.

recallprecision

)recall*precision(*2

measure_F





(3)

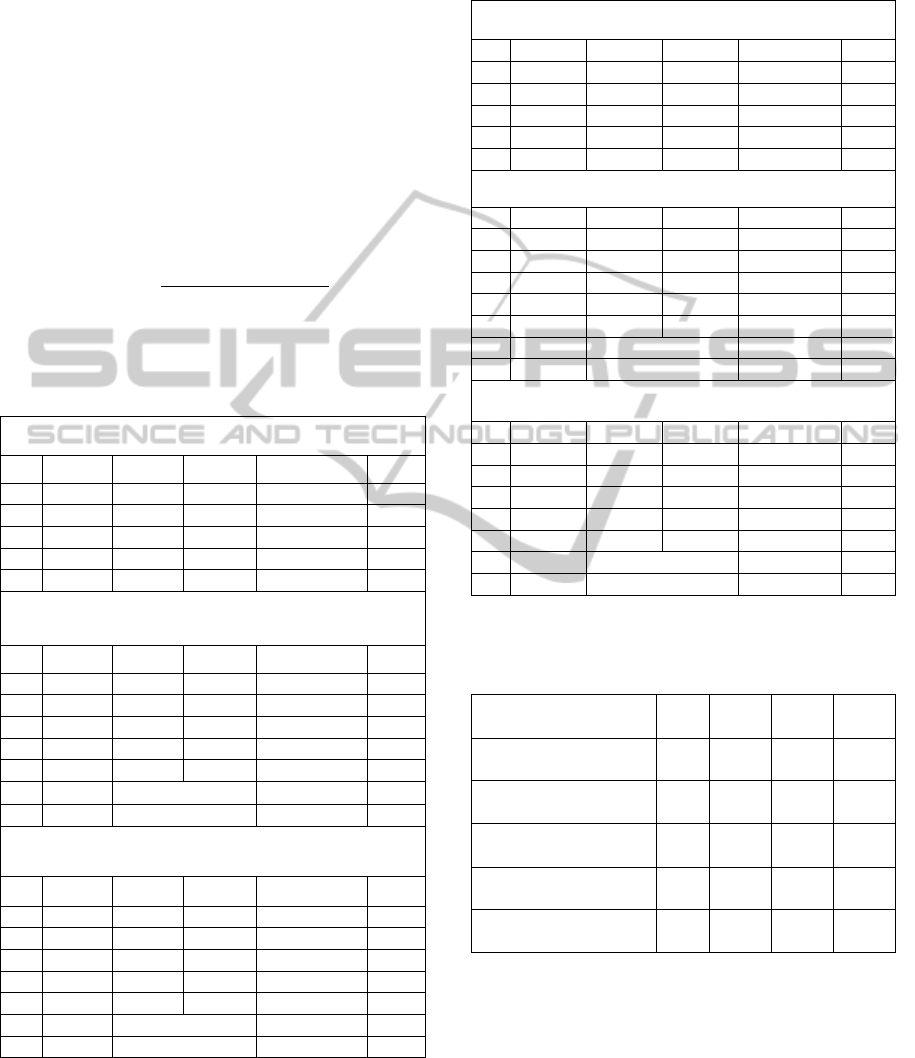
Table 1: Confusion matrix and accuracies for the three

classes of secondary structures, for data without feature

scaling, using ELM-PSO, SVM and Naïve Bayes.

Confusion Matrix – ELM-PSO – without feature scaling

H E C % correct

H 1147 116 457 66.7 QH

E 300 329 474 27.1 QE

C 604 175 1195 30.6 QC

Total 4797

55.7 Q3

Confusion Matrix – SVM – without feature scaling

H E C % correct

H 3153 533 1672 58.8 QH

E 817 1353 1411 22.8 QE

C 1446 595 5083 20.5 QC

Total 16063

59.7 Q3

F-Measure

58.5

AUC

70.0

Confusion Matrix – Naïve Bayes – No feature scaling

H E C % correct

H 3244 1217 897 60 QH

E 705 2168 708 60 QE

C 2028 2168 708 47.6 QC

Total 16063

54.8 Q3

F-Measure 55.1

AUC 73.5

Table 2: Confusion matrix for the three classes of

secondary structures, for data with feature scaling, using

ELM-PSO, SVM and Naïve Bayes.

Confusion Matrix – ELM-PSO – with feature scaling

H E C % correct

H 1814 0 0 100 QH

E 56 942 94.3 QE

C 224 0 1799 89.9 QC

Total 4835

94.4 Q3

Confusion Matrix – SVM - with feature scaling

H E C % correct

H 24854 67 8 99.7 QH

E 0 16879 4 100 QE

C 0 0 31096 100 QC

Total 72908

99.9 Q3

F- Measure 99.8

AUC 99.9

Confusion Matrix – Naïve Bayes - with feature scaling

H E C % correct

H 24896 33 0 99.9 QH

E 256 16627 0 98.5 QE

C 0 19 31077 99.9 QC

Total 72908

99.6 Q3

F- Measure 99.6

AUC 100

Table 3: Comparison of results for secondary structure

prediction using ELM-PSO - feature scaled data, with

other studies in literature.

Method

( %)

(%)

PHD (Rost and

Sander, 1999)

70.8 72.2 66.0 72.0

JNet server (Cuff and

Barton, 2000)

76.4 78.4 63.9 80.6

SVMpsi (Kim and

Park, 2003)

76.6 78.1 65.6 81.1

SPINE server (Dor

and Zhou, 2007)

80.0 84.44 72.23 80.46

ELM-PSO with

feature scaling

94.4

100 94.3 89.9

5 CONCLUSIONS

A two stage approach for secondary structure

prediction was presented where an Extreme

Learning Machine (neural network) was used along

with Particle Swarm Optimization (ELM-PSO) for

classifying a reduced set of three secondary

ICFC 2010 - International Conference on Fuzzy Computation

374

structures, namely, alpha-helix, beta-strand and coil.

The data was generated using CABS potential

energy. ELM-PSO needs improvement to achieve

better accuracies on blind tests so that comparative

results can be achieved on new proteins.

ACKNOWLEDGEMENTS

We thank Pawel Gniewk, a student at ‘Theory of

Biopolymers, Faculty of Chemistry, Warsaw

University’, whose original idea and algorithm was

used to generate the potentials data that was used for

the secondary structure predictions. We

acknowledge the support of National Institutes of

Health through grants R01GM081680,

R01GM072014, and R01GM073095 and the support

of the NSF grant through IGERT-0504304.

REFERENCES

Altschul, S., Madden, T., and Schaffer, A., 1997. Gapped

BLAST and PSI-BLAST: a new generation of protein

database search programs. Nucl Acids Res, 25, 3389 –

3402.

Clerc, M. K. and Kennedy, J., 2002. The particle swarm -

explosion, stability, and convergence in a

multidimensional complex space. IEEE Trans

olutionary Comput, 6 (1) 58-73.

Chou, P. Y. and Fasman, G. D., 1974. Prediction of protein

conformation. Biochemistry, 13(2), 222-245.

Cole, C., Barber, J. D., and Barton , G. J., 2008. The Jpred

3 secondary structure prediction server. Nucleic Acids

Research, 36 (Web Server issue): W197–W201.

Cuff, J. A. and Barton, G. J., 2000. Application of multiple

sequence alignment profiles to improve protein

secondary structure prediction. Proteins, 40(3), 502-

511.

Dor, O. and Zhou, Y., 2007. Achieving 80% Ten-fold

Cross-validated Accuracy for Secondary Structure

Prediction by Large-scale Training. PROTEINS:

Structure, Function, and Bioinformatics, 66, 838-845.

Garnier, J., Osguthorpe, D. J. and Robson, B., 1978.

Analysis of the accuracy and implications of simple

methods for predicting the secondary structure of

globular proteins. J Mol Biol, 1, 97-120.

Garnier, J., Gibrat, J. F., and Robson, B., 1996. GOR

secondary structure prediction method version IV.

Methods Enzymol, 226, 540-553.

Huang, G. B., Zhu, Q. Y., and Siew, C. K., 2006. Extreme

learning machine: Theory and applications.

Neurocomputing, 70(1-3), 489-501.

Jones, D., 1999. Protein secondary structure prediction

based on position-specific scoring matrices. J Mol

Biol, 292, 195 – 202.

Kabsch, W. and Sander, C., 1983. Dictionary of protein

secondary structure: pattern recognition of hydrogen-

bonded and geometrical features. Biopolymers, 22(12),

2577-2637.

Kihara, D., 2005. The effect of long-range interactions on

the secondary structure formation of proteins. Prot

Sci., 14( 8), 1955–1963.

Kim, H. and Park, H., 2003. Protein Secondary Structure

Prediction Based on an Improved Support Vector

Machines Approach. Protein Eng, 16, 553-560.

Kloczkowski, A., Ting, K. L., Jernigan, R. L., and Garnier,

J., 2002. Combining the GOR V algorithm with

evolutionary information for protein secondary

structure prediction from amino acid sequence.

Proteins, 49, 154-166.

Kolinski A., 2004. Protein modeling and structure

prediction with a reduced representation. Acta Biochim

Pol, 51, 349-371.

Lomize, A. L., Pogozheva, I. D. and Mosberg, H. I., 1999.

Prediction of protein structure : The problem of fold

multiplicity. Proteins, 37, 199-203.

Montgomerie, S., Sundaraj, S., Gallin W., and Wishart, D.,

2006. Improving the Accuracy of Protein Secondary

Structure Prediction Using Structural Alignment. BMC

Bioinformatics, 7, 301.

Ortiz,

A. R., Kolinski, A., Rotkiewicz, P., Ilkowski, B. and

Skolnick, J., 1999. Ab initio folding of proteins using

restraints derived from evolutionary information.

Proteins Suppl 3 (CASP3 Proceedings), 177-185.

Pollastri, G., Martin, A., Mooney, C. and Vullo, A., 2007.

Accurate prediction of protein secondary structure and

solvent accessibility by consensus combiners of

sequence and structure information. BMC

Bioinformatics, 8(1), 201.

Qian, N. and Sejnowski, T. J., 1988. Predicting the

secondary structure of globular proteins using neural

network models. J Mol Biol, 202, 865-884.

Rost, B. and Sander, C., 1993. Prediction of protein

secondary structure at better than 70% accuracy. J.

Mol. Biol., 232, 584–599.

Rost, B., 2001. Review: Protein Secondary Structure

Prediction Continues to Rise. J Struct Bio, 134, (2-3),

204-218.

Rost, B., Yachdav, G. and Liu, J., 2004. The PredictProtein

Server, Nucl Acids Res, 32, Web Server issue, W321-

W326.

Saraswathi, S., Suresh, S., Sundararajan, N., Zimmerman,

M. and Nilsen-Hamilton, M., 2010. ICGA-PSO-ELM

approach for Accurate Cancer Classification Resulting

in Reduced Gene Sets Involved in Cellular Interface

with the Microenvironment. IEEE Transactions in

Bioinformatics and Computational Biology,

http://www.computer.org/portal/web/csdl/doi/10.1109/

TCBB.2010.13.

Ward, J. J., McGuffin, L. J., Buxton, B. F. and Jones, D.

T., 2003. Secondary structure prediction with support

vector machines. Bioinformatics, 19(13), 1650-1655.

Witten, I. H. and Frank, E., 2005. Data Mining: Practical

machine learning tools and techniques, (2nd ed.) San

Francisco: Morgan Kaufmann.

PROTEIN SECONDARY STRUCTURE PREDICTION USING KNOWLEDGE-BASED POTENTIALS

375