INVESTIGATING REPLACEMENT STRATEGIES FOR THE

ADAPTIVE DISSORTATIVE MATING GENETIC ALGORITHM

Carlos M. Fernandes, Juan Julián Merelo

Department of Computers’ Architecture, University of Granada, Granada, Spain

Agostinho C. Rosa

Department of Electrotechnics, Technical University of Lisbon, Lisbon, Portugal

Keywords: Genetic algorithms, Dissortative mating, Dynamic optimization problems.

Abstract: This paper investigates the effects of modifying the Adaptive Dissortative Mating Genetic Algorithm

(ADMGA) replacement strategy on the performance of the algorithm in dynamic problems. ADMGA is a

variation of the standard GA with a mating restriction based on the genotypic similarity of the individuals.

Dissimilar individuals mate more often than expected by chance and, as a result, genetic diversity

throughout the run is maintained at a higher level. ADMGA was previously tested in dynamic optimization

problems with promising results: the algorithm shows to outperform standard GAs and state-of-the-art

approaches on several problems and dynamics. However, the performance of the algorithm degrades when

the frequency of changes increases. Due to the premises under which ADMGA was tested, it has been

argued that the replacement strategy that emerges from the algorithm’s dissortative mating strategy may be

harming the performance in such situations. This study proposes alternative replacement schemes with the

objective of improving ADMGA’s performance on fast changing environments (without damaging the

performance on slower ones). The strategies maintain the simplicity of the algorithm, i.e., the parameter set

is not increased. The replacement schemes were tested in dynamic environments based on stationary

functions with different characteristics, showing to improve standard ADMGA’s performance in fast

dynamic problems.

1 INTRODUCTION

In the last two decades, Evolutionary Algorithms

have been successfully applied in industrial

problems, especially those with non-linearities and

multiple objectives. However, real-world problems

often have dynamic components that lead to

(predictable or unpredictable) variations of the

fitness function, i.e., the problem is defined by a

time-varying fitness function.

A problem is said to be dynamic when there is a

change in the fitness function, problem instance or

restrictions, thus making the optimum change as

well. In each period of optimization, the fitness

function is deterministic, but when changes occur,

solutions already found may be no longer valid and

the process must engage in a new search effort.

Evolutionary Algorithms’ (EAs) self-adaptive

characteristics make them promising candidates to

solve this type of problems.

Nowadays, these research efforts on evolutionary

dynamic optimization are being mainly directed

towards diversity maintenance techniques and

memory schemes. There are other possible

approaches, like reacting to changes (Cobb, 1990)

when they occur, or using multi-populations (Branke

et al., 2000), or even tackle the change with a new

randomly generated population, but the performance

of such kind of approaches is strongly dependent on

the intensity of the changes — they perform better

when changes affect a small percentage of the

genotype’s variables — and, usually, require that the

changes are easy to detect. Moreover, even if the

change is easy to detect, it is hard to decide whether

it is better to restart the population or continue the

search with the same population after a shift in the

environment. Thus, it is sometimes better to have an

algorithm that is capable of continuously adapting

104

Fernandes C., Merelo J. and Rosa A..

INVESTIGATING REPLACEMENT STRATEGIES FOR THE ADAPTIVE DISSORTATIVE MATING GENETIC ALGORITHM.

DOI: 10.5220/0003087001040113

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 104-113

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

the solution to a changing environment — for

instance, by reusing the information gained in the

past via a memory. For a description of a possible

set of categories to classify evolutionary approaches

to dynamic problems, please refer to (Branke, 2001).

Memory schemes (Goldberg & Smith, 1987;

Ramsey & Grefenstette, 1998) may be very effective

in some situations, and overcome some of the

aforementioned difficulties but their utility is

believed to be restricted to a certain type of

dynamics — in general, memory is particularly

useful when the dynamics of change is circular, i.e.,

the shape of the fitness landscape repeats from time

to time. In addition, they require a considerable

tuning effort and some parts of their design and

implementation may be not trivial (Branke, 1999).

Diversity maintenance techniques (Grefenstette,

1992; Yang, 2008; Tinós & Yang, 2007; Fernandes

et al., 2008c) usually slow down the convergence of

the algorithm during the stationary periods, a

characteristic that may harm the performance when

the changes in the fitness function are separated by

short periods of time (high frequency of changes).

However, these approaches do not require, in

general, any knowledge about the problem and

neither its dynamics nor its performance is reported

to be highly dependent on a specific configuration of

the problem.

A possible approach for designing diversity

maintenance EAs for dynamic optimization is using

mating restrictions based on the genotypes.

Dissortative mating, for instance, which refers to

mating strategies in which dissimilar individuals

mate more often than expected by chance, may be

inserted into to an EA and slow down the diversity

loss. There are several EAs in the literature with

such type of mating strategies. One of them is the

Adaptive Dissortative Mating Genetic Algorithm

(ADMGA), proposed by Fernandes and Rosa

(2008a) and applied to dynamic optimization with

promising results in (Fernandes & Rosa, 2008b;

Fernandes, 2009). However, it has been observed

that its performance degrades when the frequency of

changes increases. One of the possible explanations

for this behavior resides in the replacement strategy

and the premises under which it is tested: since

changes are assumed to be hard to detect, the

algorithm reevaluates every solution that remains in

the population after one generation (Please note that

this is the worst case scenario; in many applications

the changes may be detected with less computational

effort).

This problem arises because ADMGA’s

population replacement procedure is a population-

wide elitist strategy (Thierens, 1999): parents and

children compete and live in the same population. It

has been shown (Fernandes, 2009) that if every old

solution is reevaluated, then the average ratio

between ADMGA’s new individuals and function

evaluations, in each generation, is approximately ½.

In addition, since the replacement strategy is elitist,

it tends to reduce diversity. This may be slowing

down ADMGA and the effect is much more

pronounced with high frequency of changes because

there are fewer evaluations them.

This paper addresses this issue by proposing

alternative replacement strategies that introduce

diversity in the ADMGA’s parents’ subpopulation.

Three different schemes are proposed: one in which

the parents that remain in the population are first

mutated and then reevaluated: Replacement Strategy

2 (RS 2); another one that replaces the parents by

mutated copies of the best individuals (RS 3);

finally, a third scheme that is inspired by the

Random Immigrants Genetic Algorithm (RIGA)

(Grefenstette, 1992) and replaces the parents that

remain in the population by randomly generated

solutions (RS 4). The three strategies are tested in

several dynamic problems designed with a dynamic

problem generator (Yang, 2003). The results are

compared to those attained by the standard

ADMGA, here also described as Replacement

Strategy 1 (RS 1). Then, the best strategy is

compared with a standard Generational Genetic

Algorithm (GGA) and with a recently proposed

evolutionary approach for dynamic optimization,

called Elitism-based Immigrants Genetic Algorithm

(EIGA) (Yang, 2008). The results demonstrate that

the best strategy (RS 2) is clearly capable of

outperforming standard ADMGA on fast

environments, without degrading its performance

when the frequency is lower. The new algorithm

increases the frequency value below which ADMGA

is better than or equivalent to GGA and EIGA.

Statistical tests are provided.

The paper is structured as follows. The following

section briefly describes the most relevant

dissortative mating strategies found in literature.

Section 3 describes ADMGA and introduces the new

replacement strategies. Section 4 describes the

experimental setup and Section 5 presents and

discusses the results. Finally, Section 6 concludes

the paper and outlines future lines of research.

2 PREVIOUS WORK

By considering merely the quality of the solutions

INVESTIGATING REPLACEMENT STRATEGIES FOR THE ADAPTIVE DISSORTATIVE MATING GENETIC

ALGORITHM

105

represented by the chromosomes when selecting

individuals for mating purposes, the traditional GAs

emulate what, in nature, is called random mating

(Russel, 1998), i.e., mating chance is independent of

genotypic or phenotypic distance between

individuals. However, random mating is not the sole

mechanism of sexual reproduction observed in

nature. Outbreeding, assortative mating and

dissortative mating (Russel, 1998) are all non-

random strategies frequently found in the behavior

of natural species. These schemes have different

effects on the genetic diversity of the population.

Take for instance dissortative mating, which is

known to increase the diversity of a population

(Russel, 1998). Assortative mating, on the other

hand, restricts mating between dissimilar individuals

and leads to diversity loss.

Therefore, dissortartive mating naturally came

out in EAs’ research field as an inspiration for

dealing with the problem of genetic diversity and

premature convergence. A well-known GA with a

dissortative mating strategy is the CHC (Eschelman,

1991). CHC uses no mutation in the classical sense

of the concept, but instead it increases the mutation

probability when the best fitness does not change

after a certain number of generations. A

reproduction restriction assures that selected pairs of

chromosomes will reproduce unless their Hamming

Distance is above a certain threshold, that is, the

algorithm restricts crossover between similar

individuals. Another possible way of inserting

assortative or dissortative mating into a GA is

described in (Fernandes & Rosa, 2001). The

negative Assortative Mating GA (nAMGA) selects,

in each recombination event, one parent, by any

method. Then, it selects a pool of  individuals —

the size of the pool controls the intensity of mating

restriction — and computes the Hamming distance

between those chromosomes and the first parent.

The individual less similar to the first parent is

selected for recombination. Although nAMGA’s

results are interesting, the size of the pool is critical

to its performance and hard to tune.

Ochoa et al. (2005) carried out an idea related

with nAMGA in a dynamic optimization framework.

Assortative and dissortative GAs are used to solve a

dynamic knapsack problem. The results show that

dissortative mating is more able to track solutions,

while a standard GA often fails to track them. The

assortative GA is the worst algorithm in the test set.

The authors also discuss the optimal mutation

probability for different strategies, concluding that

the optimal value increases when the strategy goes

from dissortative to assortative. In this line of work,

there is also a study by Ochoa et al. (2006) on the

error threshold of replication in GAs with different

mating strategies that aims at shedding some light

into the relationship between mutation probabilities

and mating strategies in EAs. The report reinforces

the idea that any experimental study on non-random

mating strategies for EAs must take into account

several mutation probability values; otherwise, the

results are probably biased towards a specific

strategy.

Besides the above-referred techniques, a large

number of other GAs with non-random mating are

found in the literature. Due to their characteristics,

these GAs are worthwhile exploring as diversity

maintenance schemes for dynamic optimization.

3 ADMGA AND REPLACEMENT

STRATEGIES

There are many possible replacement strategies

for

GAs but, in general, they may be classified into two

categories: generational and elitist. Generational

GAs replace the entire parents’ population by the

children; in elitist strategies, offspring has to

compete with their parents. ADMGA, due to its

specific design, is a population-wide elitist strategy

(Thierens, 1999). This means that some individuals

may remain in the population for more than one

generation. Since changes in non-stationary

functions are not always easy to detect, the most

reliable way to guarantee that a fitness value does

not become outdated by a change in the environment

is to reevaluate all the chromosomes that remain in

the population after reproduction. Assuming this

worst case scenario does not affect generational

GAs, because the entire population is replaced by

the offspring in each generation, and  fitness values

must be always computed — where  is the

population size —, independently of the premises.

As for an elitist GA, assuming that changes are

very hard to detect means that old individuals must

be reevaluated and that the average ratio between

new solutions and function evaluations, in each

generation, is below 1. In the particular case of

ADMGA, it has been shown (Fernandes, 2009) for

several problems that this ratio is approximately ½,

meaning that, ADMGA generates only half of the

solutions that a standard generational GA is able to

We call replacement strategy to the procedure that, from the

population of parents P(t) and the population of offspring P’(t),

selects the individuals that form the population P(t+1) and then

replace population P(t).

ICEC 2010 - International Conference on Evolutionary Computation

106

generate in the same period of time. This may be

particularly penalizing when the frequency of

changes is high, and, in fact, ADMGA’s

performance has been shown to degrade in those

situations. The question is: is it possible to improve

ADMGA’s performance in fast dynamic problems

by changing the replacement strategy in a way that

those reevaluations are accompanied by the

introduction of new genetic material in the

population? To assess this hypothesis, we test three

alternative replacement strategies. Before discussing

them, let us describe the main algorithm.

ADMGA is a self-regulated dissortative mating

EA, which incorporates an adaptive Hamming

distance mating restriction that tends to relax as the

search process advances. After two parents are

selected, crossover only occurs if the Hamming

distance between them is found to be above a

threshold value. If not, the recombination event is

classified as failed and another pair of individuals is

selected until 2

⁄

pair have tried to recombine ( is

the population size).

ADMGA

initialize population P(t) with size N

evaluate population P(t)

set initial threshold ts(0)

while (not termination condition)

create new individuals P’(t)

evaluate new individuals P’ (t)

create new population // see figure 2

end while

Procedure: create new individuals

matingEvents ← /2;

successfulMating ← 0;

failedMating ← 0

while (successfulMatings < 1) do

for (i ← 1 to matingEvents) do

select two chromosomes (c

, c

)

compute Hamming distance H(c

, c

)

if (H(c

, c

) >= ts(t))

crossover and mutate

successfulMating ← successfulMating+1

end if

if (H(c

, c

) < ts(t)) failedMating

←failedlMating+1

end for

if (failedMating > successfulMating) ts(t+1)← ts(t)-

else ts(t+1) ← ts(t)+1

end while

Figure 1: ADMGA’s pseudo-code.

After the reproduction cycle is completed, a new

population is created by selecting the  members

amongst the parents and newly generated offspring.

Then, the threshold is incremented when the number

of successful matings is greater or equal than the

number of failed matings, and it is decremented

otherwise (see pseudo-code in figure 1). This way,

the genetic diversity indirectly controls the threshold

value. When diversity is decreased, threshold tends

to be decremented because the frequency of

unsuccessful mating will necessarily increase.

However, mutation introduces variability in the

population, resulting in occasional increments of the

threshold that moves it away from 0. The only

parameters that need to be tuned in ADMGA is

population size  and mutation probability 



Crossover probability is not used (in a way, 



somewhat adaptive, because selected individuals

recombine or not depending on their Hamming

distance and the threshold value). As for the

threshold, ADMGA has shown to be capable of self-

adapting its value in the first generation, and

therefore threshold may be set to its highest possible

value (1, where  is the chromosome length) in

the beginning of the run. However, in order to avoid

initial generations in which the ratio between new

individuals and function evaluations is very low, an

initial threshold value of 4

⁄

is used when

optimizing non-stationary functions.

RS 1

insert best ’ individuals from P(t) into P’(t)

P(t+1) ← P’(t)´

//  is the size o P(t) and ’ is the size of P’(t)

RS 2

insert mutated best ’ individuals from P(t) into

P’(t)

P(t+1) ← P’(t)

RS 3

insert ’ copies of mutated best from P(t) into

P’(t)

P(t+1) ← P’(t)

RS 4

insert ’ random solutions into P’(t)

P(t+1) ← P’(t)

Figure 2: ADMGA’s create new population procedure:

replacement strategies (RS).

DMGA was tested in dynamic optimization

problems and it showed to outperform a standard

generationl GA, a standard population-wide elitist

GA, RIGA, EIGA and the Self-Organized Criticality

RIGA (SORIGA) (Tinós & Yang, 2007) on several

problems and dynamics (Fernandes, 2009).

However, when the frequency of changes is high,

ADGMA’s performance when compared to the other

INVESTIGATING REPLACEMENT STRATEGIES FOR THE ADAPTIVE DISSORTATIVE MATING GENETIC

ALGORITHM

107

algorithms diminishes. In order to overcome this

difficulty, three different replacement strategies are

introduced. Figure 2 describes these replacement

strategies, as well as the original scheme used for

dynamic optimization (RS 1). Please note that every

strategy inserts the offspring into the new

population. The differences reside in the way in

which the remaining slots are occupied — that is,

 slots, where  is the population size and ’ is

the offspring population size.

Replacement strategy 1 (RS 1) — original

ADMGA’s strategy — inserts the  best

individuals from the parents’ population into the

new population. Replacement strategy 2 (RS 2) fills

up the remaining slots with mutated copies of the

’ best individuals in parents’ population (with

mutation probability 



). Replacement strategy 3

(RS 3) inserts ’ mutated copies of the best

solution. Finally, strategy 4 (RS 4) inserts random

immigrants — i.e., randomly generated genotypes

— into the vacant slots. The following section

describes the problems used to test the efficiency of

the algorithms.

4 EXPERIMENTAL SETUP

The experiments were conducted with dynamic

versions of an order-3 trap function, an onemax

problem and the 01 knapsack problem. This way

we have, in the test set, a simple linear function

(onemax), a quasi-deceptive trap function (order-3

trap) and a combinatorial problem (knapsack). The

stationary functions were then used to construct

dynamic versions via the dynamic problem

generator proposed in (Yang, 2003) This section

describes the stationary functions, the dynamic

problem generator, and the methodology followed

during the experiments.

The knapsack version used in these experiments

is described in (Yang & Yao, 2005). The function

has a global optimum with fitness 1853 (since the

weights are non-negative integers the global

optimum can be obtained with dynamic

programming). A trap function is a piecewise-linear

function defined on unitation (the number of ones in

a binary string) that has two distinct regions in the

search space, one leading to a global optimum and

the other leading to the local optimum. Depending

on its parameters, trap functions may be deceptive or

not. The traps in this study are defined by:













, 











1









,

(1)

where u() is the unitation function and  is the

problem size (and also the fitness of the global

optimum). With this equation, order-

traps are in

the region between deceptive and non-deceptive. For

this study, a 30 bit problem was constructed by

concatenating 10 order-3 subproblems. The fitness

of the global optimum is 30. Finally, the onemax is a

simple linear problem that consists in maximising

the number of ones in a binary string. For the

experiments, we used a 100-bit problem.

The test environment proposed in (Yang, 2003)

was then used to create a dynamic experimental

setup based on the functions described above. This

problem generator has two parameters that control

the severity of the changes and their frequency:  is

a value between 0 and 1.0 which controls the

severity of change and  defines number of

generations between changes. By changing  and 

it is possible to control two of the most important

features when testing algorithms on dynamic

optimization problems: severity () and period (

— i.e., 1

⁄

is the frequency — between changes

(Angeline, 1997). In order to evaluate an algorithm’s

configuration when solving a specific problem, the

offline performance (Tinós & Yang, 2007) — i.e.,

the best-of-generation fitness values averaged over

the total number of runs and over the data gathering

period — is first examined:



























(2)

where  is the number of generations,  is the

number of runs (30 in all the experiments) and 





is the best-of-generation fitness of generation of

run of an algorithm on a specific problem. This

value gives information on how close the GAs are

able to track the moving solution.

Problem generator’s parameter  defines the

number of generations between each change.

Because this value, if provided without the

population size , does give us enough information

on the real period between changes, in this paper we

use the number of evaluations between each change

. This does not affect the generator because if

every individual in population (with size ) is

evaluated in each generation , then  /.

For each one of the stationary problems, five

different dynamic scenarios were constructed by

setting  to 600, 1200, 2400, 4800, 9600, 19200 and

38400. As for the severity () value, it is randomly

generated in each time the function changes. The

scope of this investigation is the performance

according to the frequency of changes, and therefore

ICEC 2010 - International Conference on Evolutionary Computation

108

setting  to random values simplifies the analysis.

Every run covered 50 periods of change, i.e., 50

evaluations, with changes every  evaluations.

A GA has several parameters that model their

general behavior. We are particularly interested in

GAs’ performance when varying the mutation

probability, because evolutionary approaches that

work by maintaining population diversity at a higher

level during the search may be shifting the optimal

mutation probability to different values. For

instance, and as stated above, it has been

demonstrated that dissortative and assortative mating

increase and decrease, respectively, the optimal

mutation probability of a GA. Therefore, it is of

extreme importance to test the GAs under a

reasonable range of 



values, otherwise the results

may become biased toward some of the approaches.

Probability values 



were set to 1/2, 1/, 2/

and 4/.

The population size  also affects the

performance of the GAs, not only on static

problems, but also in dynamic environments.

Knowing the optimal size is important for

determining with accuracy the scalability of a GA

and to avoid superfluous computation effort due to a

population larger than the optimal. Although this

investigation does not aim at studying scalability or

finding the optimal population size for each

problem, a proper research method must test

different  values, otherwise there is a risk of

comparing suboptimal parameter settings and,

consequently, getting invalid conclusions. In this

study, all the algorithms were tested with 8,

16, 30, 60 and 120.

As for crossover, uniform crossover was chosen

in order to avoid taking advantage of the trap

function building blocks tight linkage, which

happens when using other traditional operators such

as one- or two-point crossover. Every algorithm in

the test set uses binary tournament (tournament size

2 is in general a fairly good selective pressure for

most problem (Thierens, 1999)).

The ADMGA versions were compared with

GGA and EIGA. EIGA is a very simple scheme that

in each generation replaces a fraction 



of the

population by mutated copies of the best solution of

the previous generation (with mutation

probability





). The author shows that the algorithm

is more effective when the changes are not too

severe. Due to its simplicity and the interesting

results reported in (Yang, 2008), EIGA was selected

as the main peer-algorithm for this study. In

addition, EIGA has some similarities with one of the

replacement strategies proposed in this paper to

improve ADMGA’s performance, which makes in a

suitable candidate for being included in the test set.

EIGA and ADMGA’s RS 4 are inspired by the

Random Immigrants GA (RIGA) (Grefenstette,

1992), which maintains diversity by introducing 



random solutions in the population in each

generation, thus guarantying that brand new genetic

material enters the population in every time step.

Although RIGA is a kind of standard GA for

evolutionary dynamic optimization experiments, the

results in (Fernandes & Rosa, 2008b) and (Yang,

2008) show that ADMGA and EIGA are able to

clearly outperform RIGA in most of the dynamic

scenarios. Therefore, we chose to remove the

algorithm from the test set in order to simplify the

study and the report. Moreover, RS 4 was found to

be the worst replacement strategy in the test set,

being unable to deal with the proposed dynamic

problems. RS 4 is not a proper strategy for ADMGA

and therefore, in order to simplify the graphics, it

was removed from analysis and discussion in section

GGA was tested with crossover probability set to

0.7 and 1.0. A 2-elitist GGA was also tested. The

best results were attained with 



1.0 and 2-

elitism. Like the other algorithms, EIGA was also

tested with several 



values; 



is set to 0.6 (as

suggested in (Yang, 2008)), 0.7 and 1.0; 



is set 0.2

(also, as suggested in (Yang, 2008)). Please note that

due to its design, EIGA population size 



must set

so that



1









, where  is the population

size of a standard GA that would perform the same

number of function evaluations in each generation.

EIGA was tested with different 



values and the

results discussed in the following section refer

always to the best configurations. Please refer to

(Yang, 2008) for details on this particular issue and

on the algorithm’s implementation and parameter

tuning.

Figure 3: Experimental results with order-3 trap function.

Standard ADMGA compared with GGA and EIGA.

Population size 30; 



1

⁄

(GGA) and 





2 

⁄

(EIGA and ADMGA); 



1.0; GGA with 2-

elitism.

ε=1200 ε=2400 ε=4800 ε=9600 ε=19200

averagedoffline

performance

order‐3trap

ADMGA

GGA

EIGA

INVESTIGATING REPLACEMENT STRATEGIES FOR THE ADAPTIVE DISSORTATIVE MATING GENETIC

ALGORITHM

109

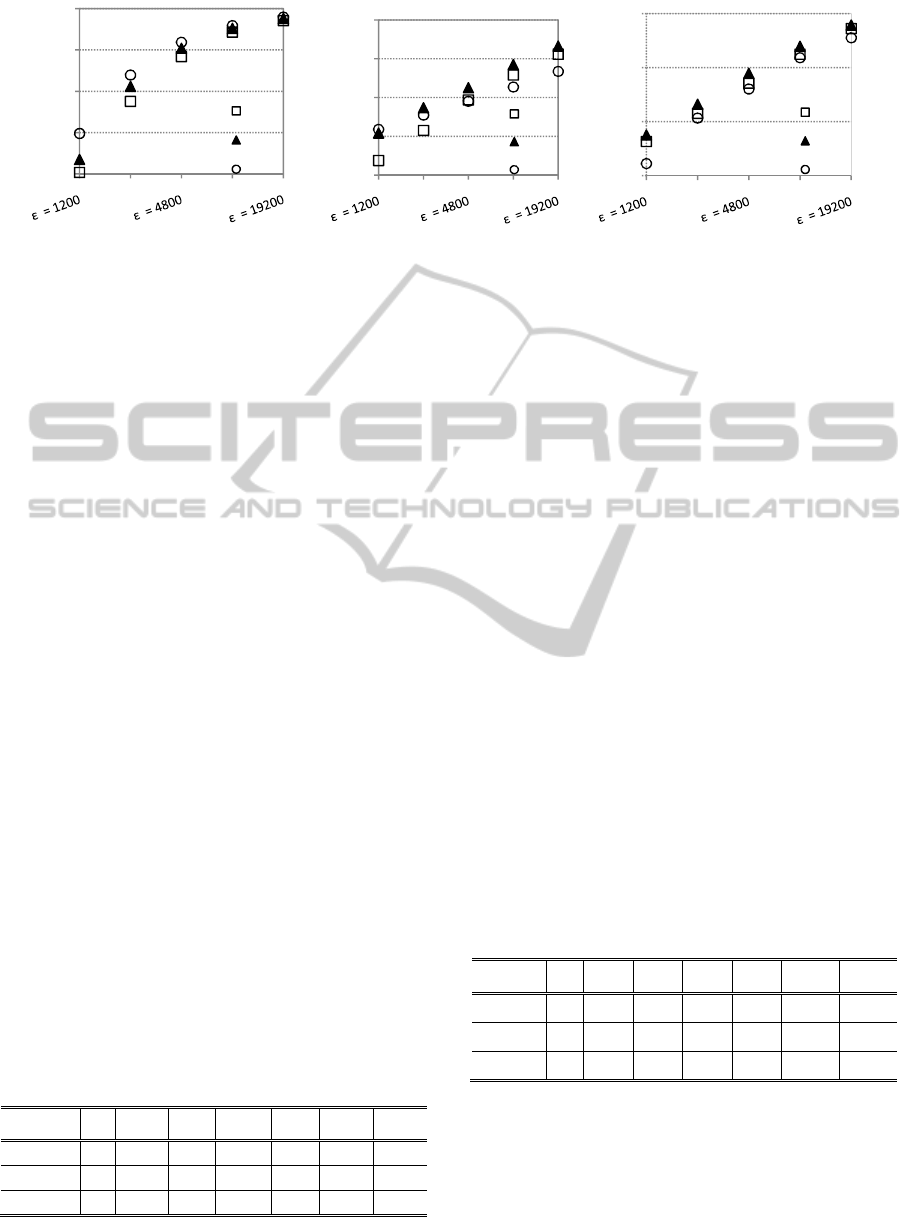
Figure 4: ADMGA replacement strategies in onemax, order-3 trap and knapsack dynamic problems. Population size:

16 (onemax) and 30 (trap and knapsack); 2/ (RS 1) and 1/ (RS 2 and RS 3). RS 2 with 2-

elitism.

5 RESULTS AND DISCUSSION

Figure 3 illustrates the issue addressed by this study.

ADMGA only outperforms the other GAs when  is

above a specific value. In the order-3 dynamic

problem, ADMGA is clearly outperformed by the

other algorithms when 4800 — an assumption

confirmed by statistical tests. The main objective is

to find a replacement strategy for ADMGA that

reduces this value. Figure 4 summarizes the results

attained by the different versions of ADMGA by

showing the configurations with  and 



values that

maximize the performance of each replacement

strategy.

The graphics show that RS 2 is capable of

outperforming standard ADMGA (RS 1) in the high

frequency scenarios. Replacement strategy 3, which

introduces mutated copies of the best individual in

the population, works well in the onemax problem,

but it is outperformed by the other strategies in most

of the dynamic scenarios based on the other two

functions. (RS 2 is 2-elitist, because this improves

its performance. Please note that RS 2 is quite

disruptive. This the payoff for having diversity

maintenance mechanisms, but the elitism guarantees

that the best solutions are not lost.)

Table 1: Kolmogorov-Smirnov tests (RS 2 vs RS1).

Results are shown as + signs when ADMGA with RS 2 is

significantly better than the ADMGA with RS 1, − when

RS 2 is significantly worst, and ≈ when the differences are

not statistically significant. Parameters as in fig. 4.

ε→ 600 1200 2400 4800 9600 19200 38400

onemax

+ + + +

≈ ≈ ≈

trap

+ + + + + + +

knapsack

+ + + + + + +

Table 1 summarizes the statistical tests conducted

on these results. RS 2 is compared with RS 1 using

Kolmogorov-Smirnov tests with 0.05 level of

significance. The tests show that RS 2 clearly

outperforms standard ADMGA (RS 1) in most of the

problems. The first objective of this study has been

accomplished: one of the schemes is able to improve

ADMGA’s performance in fast dynamic problems.

Let us now compare RS 2 with the other GAs.

Figure 5 compares ADMGA (RS 2) with GGA and

EIGA. As already stated, GGA and EIGA were

thoroughly tested in order to avoid unfair

comparisons. GGA works better with 



1.0 and

2-elitism. Best population size is 16 for

onemax, and 30 for order-3 trap and knapsack

(same values were found for the remaining

algorithms). In general,GGA’s performance is

optimized by





1

⁄

except with knapsack, where

the best is





2

⁄

Table 2: Kolmogorov-Smirnov tests (RS 2 vs GGA). The

results are shown as + signs when ADMGA with RS 2 is

significantly better than GGA, − when RS 2 is

significantly worst, and ≈ when the differences are not

statistically significant. Parameters as in figure 5.

ε→

600

1200 2400 4800 9600 19200

38400

onemax

− − ≈ ≈ ≈ ≈ ≈

trap

≈ ≈

+ + + + +

napsack

− − ≈ ≈ ≈ + +

Figure 5 and table 2 shows that for 2400,

ADMGA is never outperformed by GGA. In

particular, the  value above which ADMGA is at

least equivalent to GGA decreases from 4800 to 600

in order-3 trap (compare figures 3 and 5). Table 3

compares ADMGA with the standard strategy (RS

100

averagedofflineperformance

onemax

RS1

RS2

RS3

averagedofflineperformance

order‐3trap

RS1

RS2

RS3

1770

1790

1810

1830

averagedofflineperformance

knapsack

RS1

RS2

RS3

ICEC 2010 - International Conference on Evolutionary Computation

110

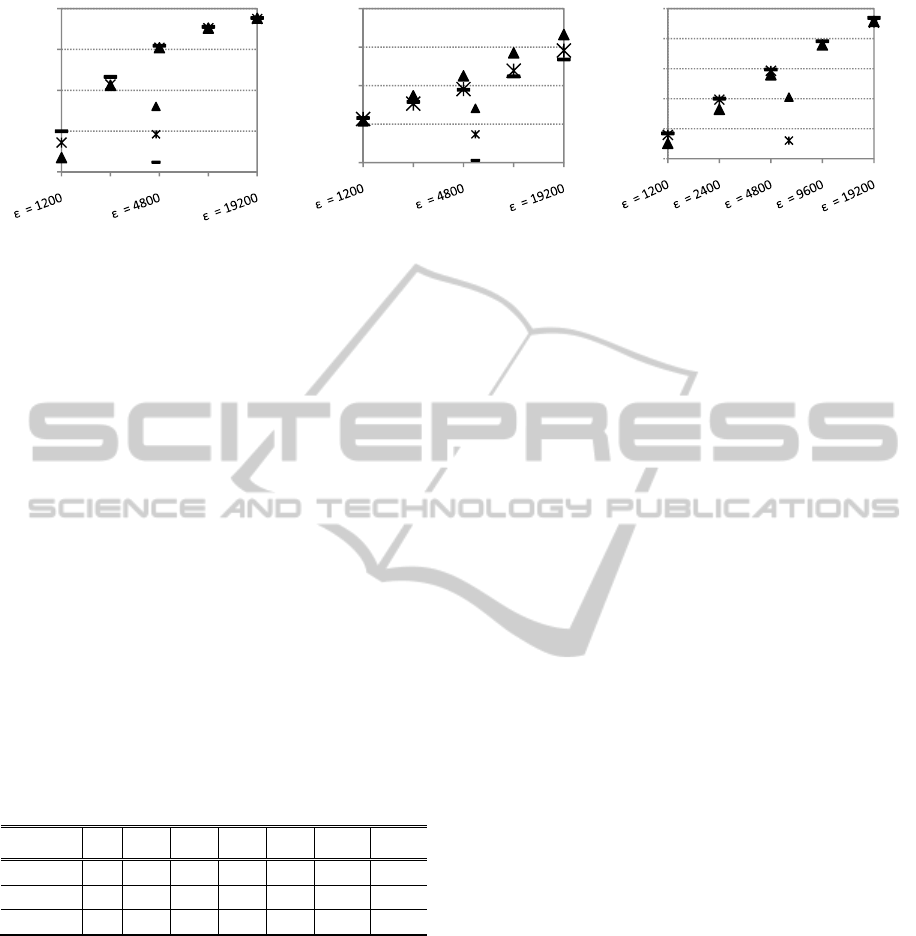
Figure 5: ADMGA (RS 2), GGA and EIGA. Parameters as in fig. 3 and 4. Population size n = 16 (onemax) and n = 30

(order-3 and knapsack). GGA with 



1

⁄

(onemax and trap) and 



2

⁄

(knapsack). EIGA with 



2

⁄

and





0.2.

1) and GGA. By comparing tables 2 and 3, it is

noticeable that RS 2 reduces the  above which

ADMGA is significantly better or at least

statistically equivalent to GGA in the dynamic

scenarios of the three base functions.

If we compare ADMGA’s replacement strategy 2

with EIGA the conclusions are similar: see figure 5

and table 4. EIGA performs better than ADMGA in

fast onemax problem and knapsack problems. On

the other hand, EIGA is outperformed by ADMGA

in almost every order-3 trap dynamic problem.

(Please note that in (Yang, 2008), EIGA is tested

with 1200 and 6000, a range that is

covered by the experiments conducted for this

paper).

Table 3: Kolmogorov-Smirnov tests (RS 1 vs GGA). The

results are shown as + signs when ADMGA with RS 1 is

significantly better than GGA, − when RS 1 is

significantly worst, and ≈ when the differences are not

statistically significant. Parameters as in figures 4 and 5.

ε→ 600 1200 2400 4800 9600 19200 38400

onemax

− − − − ≈ ≈ ≈

trap

− − − ≈

+ + +

knapsack

− − − − − ≈ +

As stated above, the comparisons in this study

were made considering the worst-case scenario, i.e.,

changes are hard to detect and a reliable detection

requires the reavaluation of the chromosomes that

are copied from previous generations. However, we

may consider a different assumption: changes are

easy to detect and all that is required is to evaluate

every old chromosomes after a change is detected.

Under these conditions, the results are different. The

summarized outcome of EIGA and ADMGA is

shown in Table 5: ADMGA clearly outperforms

EIGA in almost every dynamic problem. However,

at this point we cannot exclude the possibility of

population-wide elitism may now be biasing the

results towards ADMGA; therefore, other

experiments must be devised in order to properly

compare the GAs.

Figure 6 compares the genetic diversity, as

defined in (Fernandes, 2009), of the different

strategies. RS 2 is able to maintain diversity at a

higher level during the different periods. On the

other hand, the highly elitist strategy 3, as expected,

decreases the diversity when compared to the

standard strategy. These results may explain the

general behavior of the replacement strategies. Since

RS 2 is able to reduce diversity loss, it attains better

results throughout the test set.

6 CONCLUSIONS

This paper proposes new replacement schemes for

Adaptive Dissortative Mating Genetic Algorithm

(ADMGA). The main objective is to improve

standard ADMGA’s performance in dynamic

problems with high frequency of changes. One of

the proposed strategies outperforms the standard

strategy in most of the dynamic scenarios designed

to test the algorithms. This new strategy (RS 2)

simply mutates the chromosomes that remain in the

population after the recombination stage — the best

’ solutions in the parents’ population, where 

is the population size and ’ is the offspring

population size — before reevaluating them.

The results show that ADMGA is capable of

outperforming not only a standard GA, but also the

Elitism-based Immigrants GA (EIGA) in some

classes of problems and dynamics: 1) when the

frequency of changes is lower, ADMGA is never

outperformed by the other GAs; 2) as for higher

frequencies, ADMGA is never outperformed by

100

averagedofflineperformance

onemax

ADMGA(RS2)

GGA

EIGA

order‐3trap

ADMGA(RS2)

GGA

EIGA

1780

1790

1800

1810

1820

1830

knapsack

ADMGA(RS

GGA

INVESTIGATING REPLACEMENT STRATEGIES FOR THE ADAPTIVE DISSORTATIVE MATING GENETIC

ALGORITHM

111

GGA and EIGA in order-3 trap functions. Finally,

preliminary tests with non-stationary environments

in which the changes are easy to detect show that

ADMGA is able to outperform EIGA in every

(except one) scenario.

Table 4: Kolmogorov-Smirnov tests (RS 2 vs EIGA). The

results of the test are shown as + signs when ADMGA

with RS 2 is significantly better than EIGA, − when RS 2

is significantly worst, and ≈ when the differences are not

statistically significant. Parameters as in figure 5.

ε→

600

1200 2400 4800 9600 19200

38400

onemax

− − − ≈ ≈ ≈ ≈

trap

≈ ≈

+ + + + +

knapsack

− − ≈ ≈ ≈ ≈ ≈

One of ADMGA’s advantages over other GAs is

that it only requires two parameters that need to be

tuned ( and 



), while EIGA, for instance, requires

the setting of four parameters (, 



, 



and ).

Since EIGA has been recently proposed as a GA

specifically conceived for dynamic optimization,

and since the report in (Yang, 2008) claims that the

algorithm performs well on dynamic, we may state

that ADMGA is a viable strategy for tackling

dynamic optimization problems.

Figure 6: RS 1, 2 and 3 genetic diversity. Dynamic order-3

trap function with 2400. Parameters as in figure 4.

Table 5: Kolmogorov-Smirnov tests (RS 2 vs EIGA). The

results of the test are shown as + signs when ADMGA

with RS 2 is significantly better than EIGA, − when RS 2

is significantly worst, and ≈ when the differences are not

statistically significant. Parameters as in figure 5.

ε→

600

1200 2400 4800 9600 19200

38400

onemax

+ + + + + +

≈

trap

+ + + + + + +

knapsack

+ + + + + + +

ACKNOWLEDGEMENTS

The first author wishes to thank FCT, Ministério da

Ciência e Tecnologia, his Research Fellowship

SFRH / BPD / 66876 / 2009, also supported by FCT

(ISR/IST plurianual funding) through the

POS_Conhecimento Program. This paper has also

been funded in part by the Spanish MICYT projects

NoHNES (TIN2007-68083) and TIN2008-06491-

C04-01 and the Junta de Andalucía P06-TIC-02025

and P07-TIC-03044.

REFERENCES

Angeline, P., 1997. Tracking Extrema in Dynamic

Environments. In Proc. of the 6

International Conf.

on Evolutionary Programming, Springer, 335-345.

Branke, J., 1999. Memory enhanced evolutionary

algorithms for changing optimization problems. In

Proc. of the 1999 IEEE Congress on Evolutionary

Computation, IEEE Press, 1875-1882.

Branke, J., Kaußler, T., Schmidt, C., Schmeck, H., 2000.

A multi-population approach to dynamic optimization

problems. In Proc. of the Adaptive Computing in

Design and Manufacturing (ACDM’2000), I.C.

Parmee, Ed., London, UK: Springer-Verlag, 299-308.

Branke, J., 2001. Evolutionary optimization in dynamic

environments. Norwel, MA: Kluwer.

Cobb, H. G., 1990. An investigation into the use of

hypermutation as an adaptive operator in GAs having

continuous, time-dependent nonstationary

environments. Technical Report AIC-90-001, Naval

Research Laboratory, Washington, USA.

Eschelman, L. J., Schaffer, J. D., 1991. Preventing

premature convergence in genetic algorithms by

preventing incest. In Proc. of the 4

International

Conference on Genetic Algorithms, Morgan

Kauffman, San Francisco, 115-122.

Fernandes, C. M., Rosa, A. C., 2001. A Study on Non-

Random Mating in Evolutionary Algorithms Using a

Royal Road Function. In Proc. of the 2001 Congress

on Evolutionary Computation, IEEE Press, 60-66.

Fernandes, C. M., Rosa, A. C., 2008. Self-adjusting the

intensity of dissortative mating of genetic algorithms.

Journal of Soft Computing, vol. 12, 955-979.

Fernandes, C. M., Rosa, A. C., 2008. Evolutionary

Algorithms with Dissortative Mating on Static and

Dynamic Environments. Advances in Evolutionary

Algorithms, W. Kosinski Ed., In-Tech, 181-206.

Fernandes, C. M., Merelo, J. J., Ramos, V., Rosa, A. C.,

2008. A Self-Organized Criticality Mutation Operator

for Dynamic Optimization Problems. In Proc. of the

2008 Genetic and Evolutionary Computation

Conference, ACM Press, pp. 937-944.

Fernandes, C. M., 2009. Diversity-enhanced Genetic

Algorithms for dynamic optimization. Ph.D Thesis,

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0 4800 9600 14400 19200 24000

geneticdiversity

functionevaluations

order‐3trap

RS1

RS2

RS3

ICEC 2010 - International Conference on Evolutionary Computation

112

Tec. Univ. of Lisbon, (http://geneura.ugr.es/pub/

tesis/PhD-CFernandes.pdf)

Goldberg, D. E., Smith, R. E., 1987. Nonstationary

function optimization using genetic algorithms with

dominance and diploidy. In Proc. of the 2nd

International Conference on Genetic Algorithms, New

Jersey, 1987, 59-68.

Grefenstette, J. J., 1992. Genetic algorithms for changing

environments. In Parallel Problem Solving from

Nature II, R. Manner and B. Manderick, Eds., North-

Holland, Amsterdam, 137-144.

Ochoa, G., Madler-Kron, C., Rodriguez, R., Jaffe, K.,

2005. Assortative mating in genetic algorithms for

dynamic problems. In Proc. of the 2005

EvoWorkshops, LNCS 3449, Springer, pp. 617-622.

Ochoa, G., 2006, Error Thresholds in Genetic Algorithms.

Evolutionary Computation, 14(2), 157-182.

Ramsey, C. L., Grefenstette, J. J., 1993. Case-based

initialization of genetic algorithms. In Proc. of the 5

International Conference Genetic Algorithms, Morgan

Kaufmann, 84–91.

P. J. Russel, Genetics. Benjamin/Cummings, 1998.

Thierens, D., 1999. Scalability problems of simple GAs.

Evolutionary Computation 7(4), 331-352.

Tinós, R., Yang, S., 2007. A self-organizing random

immigrants GA for dynamic optimization problems.

Genetic Programming and Evolvable Machines 8(3),

255-286.

Yang, S., 2003. Non-stationary problem optimization

using the primal-dual genetic algorithm. In Proc. of

the 2003 IEEE Congress on Evolutionary

Computation, Vol. 3, 2246-2253.

Yang, S. Yao, X., 2005. Experimental study on PBIL

algorithms for dynamic optimization problems. Soft

Computing 9(11),815-834.

Yang, S., 2008. Genetic Algorithms with Memory- and

Elitism-Based Immigrants in Dynamic Environments.

Evolutionary Computation 16(3), 385-416.

INVESTIGATING REPLACEMENT STRATEGIES FOR THE ADAPTIVE DISSORTATIVE MATING GENETIC

ALGORITHM

113