KEYWORDS EXTRACTION

Selecting Keywords in Natural Language Texts with Markov Chains

and Neural Networks

Bła

zej Zyglarski and Piotr Bała

Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina St. 13/18, Torun, Poland

Keywords:

Keywords extraction, Text mining, Neural networks, Kohonen, Markov chains.

Abstract:

In this paper we show our approach to keywords extraction by natural language processing. We present revised

and extended version of previously shown document analysis method, based on Khonen Neural Networks with

Reinforcement, which uses data from the large document repository to check and improve results. We describe

new improvements, which we’ve achieved with preprocessing set of words and creating initial ranking using

Markov Chains. Our method shows, that keywords can be selected from the text with great accuracy. In this

paper we present evaluation and comparison of both methods and example results of keywords selection upon

random documents.

1 INTRODUCTION

Large increase of available data can be noticed nowa-

days. Modern search engines use simple language

querying and return results containing query words.

Most of the results are unfortunatelyinadequate to the

question. It shows that very important modern com-

puter science problems is automatic analysis of data,

which is able to pinpoint most important parts of data.

Problem is easier, if the data is structurised and the

structure is known (e.g. speciﬁc databases). Chal-

lenge is to ﬁnd the structure in "free language". We

have developed algorithms, which can analyse text

with use of structual distance between words and Ko-

honen Neural Networks with Reinforcement based on

previously computed distances between documents in

the large repository (see (Zyglarski and Bała, 2009)).

It means that effective keywords selection needs a

large knowledge about background information such

as other documents. This approach is similar to hu-

man learning, which can be more effective, if a per-

son knows more. In this article we introduce extended

version of this algorithm, imporooved by text prepro-

cessing and computing initial words weights (instead

of using 1 as startup weights) with use of Markov

Chains built on idea of PageRank.

2 NEURAL NETWORKS

CATEGORIZATION

ALGORITHM

Our idea of keywords selection used a distance be-

tween words deﬁneded as:

Lets

T( f) be a text extracted from a docu-

ment f and

(i) be a word placed at the position i

in this text. Lets denote the distance between words A

and B within the text

as δ

(A,B).

(A,B) = (1)

= min

i, j∈{1,..,n}

{ki− jk;A =

(i) ∧B =

( j)} (2)

By the position i we need to understand a number of

additional characters (such as space, dots and com-

mas) read so far during reading text. Every sentence

delimiter is treated like a certain amount W of white

characters in order to avoid combining words from

separate sequences. After tests we choose differend

W for different additional characters, as is shown in

table 1

The knowledge of distances between words in

document was used to categorize them with use of the

self-organizing Kohonen Neural Network (ﬁgure 1)

(Kohonen, 1998).

The categorization procedure consisted of 5 steps:

1. Create rectangular m ×m network, where m =

⌊

√

n⌋, where n is number of all words Presented

315

Zyglarski B. and Bała P..

KEYWORDS EXTRACTION - Selecting Keywords in Natural Language Texts with Markov Chains and Neural Networks.

DOI: 10.5220/0003088003150321

In Proceedings of the International Conference on Knowledge Management and Information Sharing (KMIS-2010), pages 315-321

ISBN: 978-989-8425-30-0

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Weights of additional characters.

Character Weight Reason

":", 2 weak relation

";" 10 very weak relation

".!?" 30 no relation

" " and others 1 strong relation

Figure 1: The scheme of the neural network for words cat-

egorization with selected element and its neighbors.

algorithm can distinguish maximally m

cate-

gories. Every node (denoted as ω

x,y

) is con-

nected with four neighbors and contains a proto-

type word (denoted as

(x,y)) and a set (denoted

as β

(x,y)) of locally close words.

2. For each node choose random prototype of the

category p ∈ {1,2,...,n}.

3. For each word k ∈ {1,2,..., n} choose closest

prototype

(x,y) in network and add it to list

(x,y).

4. For each network node ω

x,y

compute a general-

ized median for words from β

(x,y) and neigh-

bors lists (denoted as β). A generalized median is

deﬁned as an element A which minimizes a func-

tion:

B∈β

(A,B) (3)

Set

(x,y) = A

5. Update word weights, by checking if other docu-

ments containing actually best (highest positions

in result list) words are in fact related to analysed

one:

For random number of actually best words:

• check random number of documentscontaining

this word,

• if more than 66% is close enough to analyzed

one, increase weight of tested keyword,

• if less than 33% is close enough to analyzed

one, decrease weight of tested keyword;

6. Repeat, until the network is stable. Stability of the

network is achieved, when in two following itera-

tions all word lists are unchanged (without paying

attention to iternal lists sturcture and their position

in nodes).

Such algorithm divided the set of all words found in

document into separate subsets, which contained only

locally close words. In other words it groupped words

into related sets. During it’s workﬂow weight of each

keyword candidate was updated, by checking if this

word can be found in similar documents. Similarity

of documents was checked with use of three kinds of

distances:

Let’s S

∑

i=1..n

a S

∑

i=1..n

. Let’s de-

ﬁne distance between documents P

,...,x

) and

,...,y

) as

((x

,...,x

),(y

,...,y

)) = (4)

−

|+ |

−

|+ ... + |

−

| (5)

where x

, y

mean number of occurences of word i id

document P

and P

Let’s deﬁne distance between documents

,...,x

) i P

,...,y

) as

((x

,...,x

),(y

,...,y

)) = (6)

−y

|+ |x

−y

|+ ... + |x

−y

| (7)

where x

, y

mean number of occurences of n-gram i

ind document P

and P

Let’s deﬁne Kolmogorov distance between docu-

ments P

i P

) = (8)



K(P

∗) −K(P

∗)

K(P

)



(9)

where K(−|−) is Conditional Kolmogorov Complex-

ity.

Document X is close to document Y if X is close

to Y in the meaning of d

, d

and d

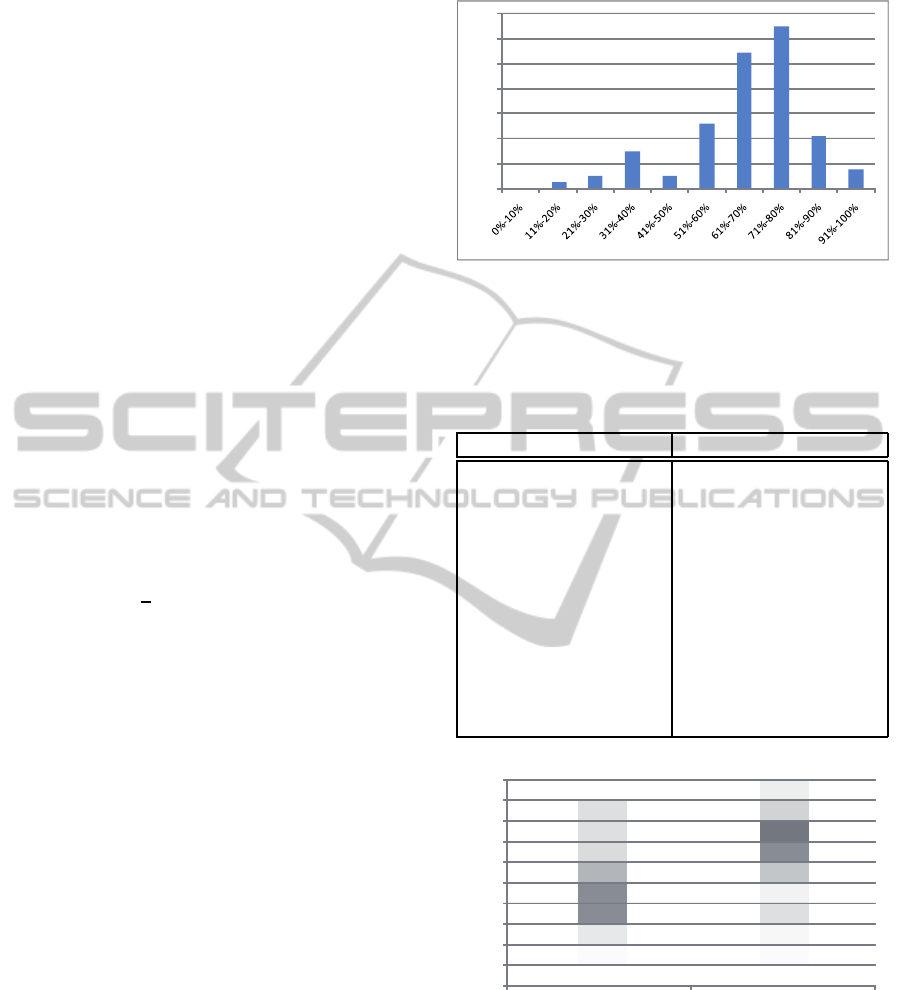
Effectivenes of this method was quite good. Tests

show that in some examples correctness of results can

achieve even 90%, but in the most cases it is about

50%-70%. Results are shown on ﬁgure 2.

3 WEIGHTS PREPROCESSING

One of the assumption of this algorithm was equal

startup weights (= 1) of all words. We show, that

preprocessing this weight can signiﬁtiantly improove

this results. This task can be performed with use of

Google PageRank idea ( (Avrachenkov and Litvak,

2004)).

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

316

10%

15%

20%

25%

30%

35%

40%

45%

Figure 2: Effects of neural network method with reinforce-

ment. X axis shows effectiveness, Y axis shows number of

documents with processed with this effectiveness.

(a) (b)

(d)

(c)

Figure 3: Example PageRank computation.

3.1 PageRank

As states in (Avrachenkov and Litvak, 2004) PageR-

ank bases on knowledge about connections between

websites. Simply the site is as important, as impor-

tant are sites linking to it.

PageRank for every site depends on number of hy-

perlinks from other sites to considered one. Any hy-

perlink is interpreted as a vote.

Assuming that {X

,...,X

} contain hyperlinks

pointing on page A, and kX

k means number of all

hyperlinks on page X

, kX

means number of hyper-

links pointing from X

to page A and PR

is PageR-

ank of X

page, and N is number of all websites in the

internet, then

1−d

+ d(PR

+ ... + PR

)

PageRank algorithm constructs matrix P =

]

i, j∈N

, where p

is a probability of moving from

page i to page j. Probability p

equals quotient of

number of hyperlinks on page i pointing on page j

and number of all hyperlinks on page i, or 0 if there

are no hyperlinks from i and j. Then transition matrix

′

= cP + (1 −c)(1/n)E is deﬁned, where E has all

elements equal to 1, and c is probability of concious

click on speciﬁc hyperlink. 1−c means random enter

to some page.

Algorithm assumes, that P(X

= s

) = p

(0) =

dla i = 1,..., n.

distribution is computed with:

(k−1), p

(k−1),..., p

(k−1)]







′

... p

′

... p

′

... p

′







= [p

(k), p

(k),..., p

(k)]

Sequence X

,...,X

,... fulﬁll assumption for being

Markov Chain and P

′

is a transition matrix and (X

)

converges to stationary distribution π.

π(P

′

) = π

π1 = 1

3.2 Markov Chains

As states in (Bremaud, 2001) and (Haggstrom, 2002):

• a sequence of random variables (X

)

n=0,...

with

values in countable set S (state space) is called

Markov Chain when ∀

n∈N

and every sequence

,...,s

∈ S

P(X

= s

n−1

= s

n−1

,...,X

= s

) = (10)

P(X

= s

n−1

= s

n−1

) (11)

if only P(X

n−1

= s

n−1

,...,X

= s

) > 0, it means

that state of chaing in time n (X

) depends only on

state in time n−1 (X

n−1

• Markov property: Matrix P = [p

]

i, j∈S

is called

transition matrix on S, if all it’s elements are pos-

itive, and sum of elements in every row equals 1.

≥ 0,

∑

k∈S

= 1 (12)

• Random variable X

is called initial state and it’s

probability distribution v(i) = P(X

= i), is called

initial distribution.

• Distribution of the Markov Chain depends on ini-

tial distribution and transition matrix.

We’ve decided to use these Markov Chains to cre-

ate a startup ranking of words inside each document.

This ranking is used as input data for main Koho-

nen Neural Network algorithm. We’ve called it Wor-

dRank.

KEYWORDS EXTRACTION - Selecting Keywords in Natural Language Texts with Markov Chains and Neural Networks

317

Table 2: Example keywords.

Example words connections

an ontology, ontology driven, driven similar-

ity, similarity algorithm, algorithm tech, tech

report, report kmi, kmi maria, maria var-

gas, vargas vera, vera and, and enrico, enrico

motta, motta an, an ontology, ontology driven,

driven similarity, driven similarity, similarity al-

gorithm, knowledge media, media institute, insti-

tute kmi, kmi the, the open, open university, uni-

versity walton, walton hall, hall milton, milton

keynes,keynes mk, mk aa, aa united, aa united,

united kingdom, kingdom m, m.vargas, vargas

vera , vera open, open.ac, ac.uk, uk abstract, ab-

stract.this, this paper, paper presents, presents our,

our similarity, similarity algorithm, algorithm be-

tween, between relations, relations in, in a, a user,

user query, query written, written in, in fol, fol

ﬁrst, ﬁrst order, order logic, logic and, and onto-

logical, ontological relations, relations.our, our

similarity, similarity algorithm, algorithm takes,

takes two, two graphs, graphs and, and produces,

produces a, a mapping, mapping between, be-

tween elements, elements of, of the, the two, two

graphs, graphs i.e, i.e.graphs, graphs associated,

graphs associated, associated to, to the, the query,

query a, a subsection, subsection of, of ontology,

ontology relevant

3.3 WordRank

While parsing simple text document, one have to ﬁnd

relations between words. Our idea of Word Rank as-

sumes using of simple natural connections between

words, based on their position upon the text. Sim-

ply we can consider two words as connected, if they

are neighbours. Additionally, according to assump-

tions presented in previous papers, initial statistical

analysis of the texts in repository was performed and

unimportant words were chosen

. They should not be

considered during connections analysis and selection

connected words. Example set of connected words is

presented in table 2. All words, which are not om-

mited, are potential keywords.

Our procedure takes following steps, shown also

on ﬁgure 4.

1. Mark all punctuation marks and all unimportant

words as division elements. Mark all other words

as potential keywords. Lets V be a set of all po-

tential keywords.

Word is unimportant if it is appearing often in all ana-

lyzed documents.

Figure 4: Example graph of connected words

2. Set as connected every two neighbor words,

which are not marked as division elements. Con-

sider each connection as bidirectional.

3. Build directed graph G = (V,E).

4. Label every connection with weight from domain

[0,1]. (E = VxVx[0,1]) Let’s x and y be two

connected words. According to carried out tests,

weight of connection between word and its suc-

cessor should equal 1 and weight of connection

between word and its predecessor should equal

0.3.

E = E ∪{(x,y,1)}∪{(y,x,0.3)} (13)

5. For each word in graph compute it’s ranking ω() :

V → [0,2].

Now main algorithm of categorization presented

in (Zyglarski and Bała, 2009) can categorize those

words and prepare ﬁnal keywords lists.

3.4 Main Part of the Algorithm

Last step of algorithm (For each word in graph com-

pute it’s ranking ω() : V → [0,2].) is the most im-

portant. It is based on the idea of Google PageR-

ank ((Page et al., 1999)), where importance of each

website depends on the number of hyperlinks, linking

to this website. Similarly in our algorithm, weight

of each word depends on weight and number of it’s

neighbors. By the word we need to understand ab-

stract class of the word (not connected with its posi-

tion in the text).

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

318

Figure 5: Example workﬂow for preprocessing weights.

Weight ω(y) of word y in time t is calculated with

∀

(y) =

+ (1− p)

∑

v∈V

ω(v,y) ∗ω

t−1

(v)

(14)

where n is number of words in the document, ω(v,w)

is the weight of the edge from v to w, and n

is a sum

of weights of all edges starting in v, and ω

(v) = 1.

p is a probability of fact, that analysed word is

keyword, while p −1 means that being keyword de-

pends on neighbor words.

While t → ∞, ω

(y) → ω(t). While repeating iter-

atively above equation, we can evaluate ω(t).

3.5 Theoretical Basis

This idea uses Markov Chains for creating Wor-

dRank.

Every step of above iteration can be represented in

matrix form.

Let’s P ∈M(n×n) = [p

]

i, j=1,...,n

be a square ma-

trix, and n means number of words in the document.

Let’s p

ω(i, j)

∑

k=1..n

ω(i,k)

, assuming, that p

= 0 if word

i wasnt neighbor of j, and vice versa. Let’s W

be a

vector of weights of all words in text in time i. Let’s

Now we can deﬁne transition matrix P

′

= [p

′

] ∈

M(n×n)

′

= p













+ (1− p)P

′

fullﬁll conditions of Markov property.

∑

j=1..n

∑

j=1..n

ω(i, j)

∑

k=1..n

ω(i,k)

(15)

∑

j=1..n

ω(i, j)

∑

k=1..n

ω(i,k)

= 1 (16)

∑

j=1..n

′

∑

j=1..n

+ (1− p)p

(17)

∑

j=1..n

∑

j=1..n

(1− p)

ω(i, j)

∑

k=1..n

ω(i,k)

(18)

= p

∑

j=1..n

+ (1− p)

∑

j=1..n

ω(i, j)

∑

k=1..n

ω(i,k)

(19)

= p + (1 − p)

∑

j=1..n

= p + 1 − p = 1 (20)

Let’s W

= P

′

i=1

. Let’s f : R

×M

n×n

(R) → R

Let’s (Z

) = P

′

∀

k∈N

and W

= E. Then chain W

i+1

f(W

i+1

) deﬁnes a Markov chain.

Proof is obvious.

Initial state of the chain is:













Then, each step of the algorithm is described by:

= P

′

i−1

and each state:







)







converges to stationary distribution W

′

, which

fullﬁlls following:

′

= P

′

Proof of Convergence. We need to show, that W

′

exists and

′

= lim

n=0..∞

This proof needs a fundamental theorem of

Markov chains, prooved in (Grinstead and Snell,

1997).

Markov chain is called regular if all elements of

some power of transition matrix are ≥ 0.

KEYWORDS EXTRACTION - Selecting Keywords in Natural Language Texts with Markov Chains and Neural Networks

319

Theorem. Let’s P be the transition matrix of reg-

ular Markov chain. Sequence of P

converges with

i → ∞ to matrix M, which all rows are equal (den-

oded as m). Additionally m is a probability vector,

which means that it’s elements are ≥ 0 and their sum

equals 1.

Matrix P

′

deﬁnes regular Markov chain.

= P

′

i−1

= P

′i

Chain W

fullﬁlls assumption of deﬁnition. Addi-

tioinally P

′n

converges to M. Any row m from matrix

M fullﬁls m = P

′

m. Let’s denote W

′

= m.

Theorem. Let’s P be the transition matrix of areg-

ular Markov chain and W = lim

n→∞

. Let’s w be a

row from W and c be a colum equal to

1. Then

1. wP = w, and every vector v such as vP = v equals

w multiplied by a scalar,

2. Pc = c and every column x such as Px = x is a

column c multiplied by a scalar.

First proof of this theorem was described by Doe-

blin in (Doeblin, 1933).

This theorem proofs, that P

′n

→W

′

with n →

∞.

Convergence speed of P

′n

→W

′

is geomethri-

cal, so we can assume that W

′

equals W

for such k,

that |W

−W

k−1

| < ε for some small ε > 0

it means

−W

k−1

| =







|ω

) −ω

k−1

|ω

) −ω

k−1

|ω

) −ω

k−1







and

∀

s=1..n

|ω

) −ω

k−1

)| < ε

4 RESULTS DISCUSSION

Usage of this preprocessing of words weights signi-

ﬁciantly improoves efﬁciency of categorization algo-

rithm.

Table 3 shows example of keywords generated for

random document with and without usage of prepro-

cessing. Comparison of both methods tested on the

set of 1000 documents is presented on ﬁgure 7.

All results were checked empirically by reading

tested documents.

As it is shown on illustration 7 new algorithm can

produce more accurate results than the previous one.

In particular cases correctness of of keywords chose

can achieve even 100%, in most cases results are 80%

correct, which is great result.

10%

15%

20%

25%

30%

35%

Figure 6: Effects of neural network method with reinforce-

ment and preprocessing of the weights. X axis shows ef-

fectiveness, Y axis shows number of documents with pro-

cessed with this effectiveness.

Table 3: Example of keywords selection with and without

preprocessing.

without preprocessing with preprocessing

component , analyses,

deep , conﬁguration ,

interface , described, ne

, generated , qa , lin-

guistic , names , stan-

dard , item , xsl , items

, extraction , grammar

, hpsg , np , id , named

, efﬁciency , evaluation

, lexical , attributes ,

semantics , elements ,

german , inﬂ , main

parsing, german,

sentence, annotation,

id, architecture, xsl,

grammar, parser,

rmrs, linguistic, com-

ponent, pos, shallow,

nlp, whiteboard, deep,

string, hybrid, en,

structures, thesis

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

KNN with Reinforcement Preprocessed Word Rank

Figure 7: Results of both algorithms.

5 FURTHER RESEARCH

Further research should touch the problem of more

accurate words distance measure. It should be con-

sidered to use some grammar relations and more so-

phisticated way to chose initial distances of words in

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

320

graph. Other area of interests is building semantics

((Shadbolt et al., 2006)) with use of generated infor-

mation.

REFERENCES

Avrachenkov, K. and Litvak, N. (2004). Decomposition of

the Google PageRank and Optimal Linking Strategy.

Research Report RR-5101, INRIA.

Avrachenkov, K. and Litvak, N. (2004). Decomposition of

the google pagerank and optimal linking strategy.

Bremaud, P. (2001). Markov Chains: Gibbs Fields, Monte

Carlo Simulation, and Queues. Springer-Verlag New

York Inc., corrected edition.

Doeblin, W. (1933). Exposé de la théorie des chains simples

constantes de markov a un nombre ﬁni d’états. Rev

Math Union Interbalkanique, 2:77–105.

Grinstead, C. M. and Snell, J. L. (1997). Introduction to

Probability. American Mathematical Society, 2 re-

vised edition.

Haggstrom, O. (2002). Finite markov chains and algorith-

mic applications.

Kohonen, T. (1998). The self-organizing map. Neurocom-

puting, 21(1-3):1–6.

Page, L., Brin, S., Motwani, R., and Winograd, T. (1999).

The pagerank citation ranking: Bringing order to the

web. Technical Report 1999-66, Stanford InfoLab.

Previous number = SIDL-WP-1999-0120.

Shadbolt, N., Berners-Lee, T., and Hall, W. (2006). The

semantic web revisited. IEEE Intelligent Systems,

21(3):96–101.

Zyglarski, B. and Bała, P. (2009). Scientiﬁc documents

management system. applikaction of kohonen neural

networks with reinforcement in keywords extraction.

In In Proceedings of IC3K 2009, pages 55–62. IN-

STICC.

KEYWORDS EXTRACTION - Selecting Keywords in Natural Language Texts with Markov Chains and Neural Networks

321