
A TRADEOFF BALANCING ALGORITHM FOR HIDING
SENSITIVE FREQUENT ITEMSETS
Harun G¨okc¸e and Osman Abul
TOBB University of Economics and Technology, S¨o˘g¨ut¨oz¨u, Ankara, Turkey
Keywords:
Data mining, Frequent itemset mining, Privacy, Sensitive knowledge hiding.
Abstract:
Sensitive frequent itemset hiding problem is typically solved by applying a sanitization process which trans-
forms the source database into a release version. The main challenge in the process is to preserve the database
utility while ensuring no sensitive knowledge is disclosed, directly or indirectly. Several algorithmic solutions
based on different approaches are proposed to solve the problem. We observe that the available algorithms are
like seesaws as far as both effectiveness and efficiency performances are considered. However, most practical
domains demand for solutions with satisfactory effectiveness/efficiency performances, i.e., solutions balanc-
ing the tradeoff between the two. Motivated from this observation, in this paper, we present yet a simple and
practical frequent itemset hiding algorithm targeting the balanced solutions. Experimental evaluation, on two
datasets, shows that the algorithm indeed achieves a good balance between the two performance criteria.
1 INTRODUCTION
Privacy preserving data mining has been an active re-
search area since O’Leary (O’Leary, 1991) has shown
that data mining is indeed a threat to database security.
The threat is due to the fact that advances in data min-
ing have resulted in tangible tools that can easily sur-
face private and sensitive knowledge. This prompts
database publishing to be done carefully. Consider
a database publishing scenario where a data owner
is enthusiastic about sharing his database with pub-
lic, and at the same time reluctant of doing so as
the database may contain sensitive knowledge that
must be kept private. Then, a safe publishing is to
remove (or conceal) those sensitive knowledge prior
to the publishing by applying a sanitization process.
This problem is known as sensitive knowledge hiding.
When the knowledge to be hidden is of the form fre-
quent itemsets, then the respective knowledge hiding
problem is called frequent itemset hiding.
Disclosure of a sensitive frequent itemset (knowl-
edge) is a violation of its privacy. To this end, a sensi-
tive itemset needs not necessarily to refer to persons.
For instance, it can simply be a surprising set of su-
permarket items frequently bought together by many
customers. Data owner can tag this itemset as sensi-
tive due to the commercial value of the knowledge.
So, mining the knowledge that ’the itemset is fre-
quent’ must be impossible from the released database.
Clearly, this requires that the original database must
be sanitized, and technically speaking, the task is ac-
complished by reducing its support.
Atallah et al. (Atallah et al., 1999) formalized
the problem of sensitive frequent itemset hiding, and
proved NP-Hardness of finding an optimal solution.
Therefore, researchers in the community have been
working on developing effective/efficient database
sanitization techniques and heuristics. Many algo-
rithms differing from each other in complexity, effi-
ciency, and effectiveness were proposed as a result of
these efforts. In this study, we show that the efficiency
gap, between quite sophisticated algorithms and very
straightforward ones, is remarkable compared to that
of effectiveness. Hence, we develop a practical al-
gorithm aimed at balancing the tradeoff. Our exper-
imental evaluation results suggest that the algorithm
achieves a good balance.
The paper is organized as follows. We first pro-
vide our motivation in the next subsection, before pre-
senting the sensitive frequent itemset hiding problem
200
Gökçe H. and Abul O..
A TRADEOFF BALANCING ALGORITHM FOR HIDING SENSITIVE FREQUENT ITEMSETS.
DOI: 10.5220/0003088302000205
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 200-205
ISBN: 978-989-8425-28-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

in Section 2. Next, Section 3 introduces our algo-
rithm, and then Section 4 gives the results of our ex-
perimental evaluation. Finally, Section 5 concludes.
1.1 Motivation
The work presented in (Abul et al., 2009) im-
plemented several sensitive frequent itemset hid-
ing algorithms from the literature. The work also
extensively compared a few algorithms on select
datasets empirically, and concluded that (i) perfor-
mance suffers on difficult problem instances as far
as effectiveness/efficiency tradeoff is concerned, and
(ii) new algorithms capable of tuning the effective-
ness/efficiency tradeoff are in demand. It also has
revealed that quite sophisticated algorithms achieve,
over relatively naive ones, a marginal gain (up to two
fold) in effectiveness at the cost of sizable (up to three
order of magnitude) loss in efficiency. Clearly, this
suggest that such algorithms may not be useful in
some practical domains such as online database pub-
lishing. Moreover, sophisticated algorithms are quite
complex and require extensive engineering for effi-
cient implementation. These observations motivated
us to developa newfrequent itemset hiding algorithm,
called BalancedHider, withs the following properties.
• simple, practical, efficient, and relatively effective
These requirements together means that Bal-
ancedHider must target a good balance between the
efficiency and effectiveness tradeoff. It achieves so by
favoring for efficiency as the gap there is remarkably
higher compared to the effectiveness gap. To illus-
trate, let our sophisticated algorithm be BorderBased-
Hider (BBHider for short) (Sun and Yu, 2005) and the
naive algorithm be CyclicHider (Atallah et al., 1999);
the details of which are reviewed in Section 2.2. We
conducted an experimental evaluation on a real world
market basket database,
Retail
(Brijs et al., 1999),
by randomly selecting 20 frequent itemsets as sensi-
tive. The itemsets are restricted to have length two or
three, and their mean support is 977.95. We evaluated
the performances at disclosure thresholds of 400, 300,
200, and 100. The efficiency and effectiveness results
at the respective disclosure thresholds are provided in
Table 1 and Table 2, respectively. The efficiency and
effectiveness results measure the runtime in seconds
and frequent itemsets lost due to the sanitization.
We see from Table 1 that CyclicHider runs re-
markably fast (up to three-four order of magnitude)
compared to BBHider. Another notable result is about
the growth rates of runtime with decreasing disclo-
sure thresholds. Note that the growth rate of BBHider
is exponential whereas that of CyclicHider is poly-
nomial. On the other hand, Table 2 clearly shows
Table 1: Efficiency (runtime in seconds) of BBHider and
CyclicHider on
Retail
.
Disc. thr.
Algorithm 400 300 200 100
BBHider
2221.6 3599.6 6704.2 20785.4
CyclicHider
1.716 1.856 1.935 2.231
Table 2: Effectiveness (the number of frequent itemsets
lost) of BBHider and CyclicHider on
Retail
.
Disc. thr.
Algorithm 400 300 200 100
BBHider
80 141 262 977
CyclicHider
140 257 466 1515
nonsens. freq. itemsets # 609 1158 2242 6645
that BBHider performs better (up to two-fold) at all
threshold levels, although the performance gap is not
as large as presented for the efficiency.
2 FREQUENT ITEMSET HIDING
Let I = {i
1
, i
2
, . . . , i
n
} be a set of items. A transac-
tion T is any non-empty subset of I and a database
D is a collection of transactions, D = {t
1
,t
2
, . . . , t
m
}.
The support set of itemset X in database D, denoted
S
D
(X), is the set of all transactions including X as
a subset. Formally, S
D
(X) = {T : X ⊆ T ∧ T ∈ D }.
The support of X in D, denoted sup
D
(X), is simply
the cardinality of S
D
(X).
Definition 1. (Frequent Itemset Mining (Agrawal
et al., 1993)) Let σ be user-defined positive inte-
ger, termed as support threshold (or simply thresh-
old). For a fixed D, any itemset having support
not less than σ is called a frequent itemset. The
set of all frequent itemsets is defined as: F
(D,σ)
=
{X : X ⊆ I, X 6=
/
0, sup
D
(X) ≥ σ}. Frequent itemset
mining is the problem of finding F
(D,σ)
.
A sample database from (Sun and Yu, 2005) is
given in Fig. 1(a). Letting the support threshold
σ = 3, the set of frequent itemsets (with respective
supports) is computed as shown in Fig. 1(b).
Since any itemset in the set of frequent itemsets
is a piece of knowledge, it can bear sensitivity that
the data owner is never willing to share it with others,
neither directly or indirectly.
Definition 2. (Frequent Itemset Hiding) Let P
h
=
X
i
| X
i
∈ 2
I
∧ i = 1, 2, . . . , n
be the set of n sensi-
tive itemsets. Given a disclosure threshold ψ, fre-
quent itemset hiding is the problem of transforming
database D to database D
′
such that:
• ∀X
i
∈ P
h
: sup
D
′
(X) < ψ.
A TRADEOFF BALANCING ALGORITHM FOR HIDING SENSITIVE FREQUENT ITEMSETS
201

Tid Items
1 abcde
2 acd
3 abdfg
4 bcde
5 abd
6 bcdfh
7 abcg
8 acde
9 acdh
(a) Sample database
a :7, b :6, c :7, d :8, e :3
ab :4, ac :5, ad :6, bc :4, bd :5, cd :6, ce :3, de :3
abd :3, acd :4, bcd :3, cde :3
(b) Frequent itemsets
Figure 1: A sample database [left], and the frequent item-
sets (σ = 3) along with their supports [right].
•
∑
X∈2
I
\P
h
| sup
D
(X) − sup
D
′
(X) | is minimized.
The transformation is called sanitization, and the
sanitized database D
′
is the released version of D .
In the definition, the first requirement (sensitivity)
asks decreasing support of all sensitive itemsets be-
low the given threshold so that none of them appears
in F
(D
′
,ψ)
. The objective with the second requirement
(distortion) is to keep D
′
as close as to D , i.e., to
maintain utility of D.
A sample frequent itemset hiding problem is illus-
trated in Fig. 2, where there are three itemsets (Fig.
2(a)) to hide from the sample database introduced in
Fig. 1(a). The database given in Fig. 2(b) is a sani-
tized database (with ψ = 3). Since all sensitive item-
sets have support less than 3, it can be safely pub-
lished as no data mining algorithm can discover any
of them as frequent at σ = 3.
acd, ad, bcd
(a) Sensitive itemsets
Tid Items
1 abce
2 cd
3 abdfg
4 bcde
5 ab
6 bcdfh
7 abcg
8 ace
9 acdh
(b) Sanitized database
Figure 2: Sensitive itemsets to be hidden from the sample
database [left], and a sanitized version (with ψ = 3) [right].
2.1 Related Work
Atallah et al. (Atallah et al., 1999) was the first work
formally defining the knowledge hiding problem in
the context of the frequent itemset hiding. An im-
portant contribution of that work is proving the NP-
Hardness of the problem. The authors also proposed
a simple reference algorithm to solve the problem. We
call their reference algorithm CyclicHider.
In (Sun and Yu, 2005), a border-based approach is
presented. The idea is to preserve the shape of posi-
tive border (of frequent itemsets) during sanitization
process as much as possible. We call their algorithm
BBHider, and present its details in Section 2.2. In
(Moustakides and Verykios, 2006), another border-
based algorithm is presented. A linear time (w.r.t.
|D|) sanitization algorithm employing sliding win-
dow approach is presented in (Oliveira and Za¨ıane,
2003). Other proposals include FHSFI (Weng et al.,
2007) and matrix-based approach (Lee et al., 2004).
Knowledge hiding in other contexts, e.g., association
rules (Verykios et al., 2004), sequential patterns (Abul
et al., 2007b), and spatio-temporal trajectories (Abul
et al., 2007a) has also been studied.
2.2 CyclicHider and BBHider
Cyclic hiding algorithm is a very simple algorithm
presented as a reference in (Atallah et al., 1999). It
hides each sensitive frequent itemset in turn and finds
its next supportingtransaction to removethe next item
in it to reduce the support by one.
A border-based approach is presented in (Sun and
Yu, 2005). The idea is to preserve the shape of posi-
tive border during the sanitization process as much as
possible. The algorithm is sketched in Algorithm 1.
The algorithm first computes the positive border,
Bd
+
, of frequent itemsets (line 1), and lower border of
sensitive itemsets (line 2). The lower border computa-
tion simply removes those itemsets from P
h
that have
proper subsets in P
h
. The itemsets in P
h
are sorted
based on descending order of size and ascending or-
der of support (line 3). The outer loop handles sen-
sitive itemsets in one-by-one fashion. For the itemset
X, the algorithm decreases its support by one at each
iteration of the inner loop. Any transaction-item pair
(T, i), where i ∈ X ⊆ T, is a hiding candidate and the
function HidingCandidates returns the hiding candi-
dates list C. Clearly, removing any candidate c fromC
reduces X’s support by one but relative costs may dif-
fer greatly. The objective with SelectCandidate is to
choose a candidate among all such that the cost w.r.t.
the positive border shape distortion is minimum. To
do so for every c ∈ C, SelectCandidate computes re-
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
202

Algorithm 1: BBHider.
Input: D, P
h
, ψ, λ
Output: D
′
1: Bd
+
← PositiveBorder(F
(D,ψ)
)
2: P
h
← LowerBorder(P
h
)
3: Sort P
h
(desc. order of size and asc. order of support)
4: for all X ∈ P
h
do
5: V ←
/
0
6: C ← HidingCandidates(X, D, Bd
+
)
7: while sup
D
(X) ≥ ψ do
8: c ← SelectCandidate(C, X, D , Bd
+
, ψ, λ)
9: C ← C \ c
10: V ← V
S
c
11: end while
12: D ← U pdate(D ,V)
13: end for
14: D
′
← D
spective impact value and picks c with the minimum
value. The selected candidates are accumulated in V
(line 10) and U pdate operation actually removes the
candidates from the database.
The algorithm is a sophisticated one as it mini-
mizes the sanitization effect on positive border and
hence retains many non-sensitive frequent itemsets in
the data mining output. However, the algorithm is not
scalable to large and dense databases, especially when
the size of positive border grows large well beyond
the size of the database. A slight improvement for
candidate selection has been provided in (Sun and Yu,
2005), but the complexity remained the same.
3 BALANCEDHIDER
This section covers our proposed algorithm,
BalancedHider, aimed at balancing the effi-
ciency/effectiveness tradeoff discussed before.
The skeleton of the algorithm is given in Algorithm
2. It is simply an enhanced version of CyclicHider,
and a simplified version of BBHider.
The algorithm first sorts the database in ascending
order of transaction size to prefer short transactions
first. This is exploited in sequential scan of support-
ing transactions (line 5). The outer loop iterates over
all sensitive itemsets and reduces support in each it-
eration of the inner loop. Note that, at each iteration
of the inner loop, the support of the active sensitive
itemset X is reduced by one by deleting an item in it
from the next supporting transaction. However, the
victim selection heuristic (lines 6-8) selects a victim
item that is shared by most of the sensitive itemsets.
Clearly, the heuristic serves to decrement the support
Algorithm 2: The Tradeoff Balancing Hiding Algo-
rithm (BalancedHider).
Input: D, P
h
, ψ
Output: D
′
1: Sort D (in asc. order of transaction length)
2: for all X ∈ P
h
do
3: Sup
X
← sup
D
(X)
4: while Sup
X
> ψ do
5: Find next T ∈ D supporting X
6: SS
P
h
(T) ← {Y :Y ∈ P
h
∧Y ⊆ T}
7: victim ← highest freq. item o f X in SS
P
h
(T)
8: Remove victim item from T
9: Sup
X
← Sup
X
− 1
10: end while
11: end for
11: D
′
← D
of as many as other sensitive itemsets with a single
item removal. In fact, the victim selection heuristic
(the efficiency bottleneck) is a simplification of can-
didate selection heuristic of BBHider.
An example operation of BalancedHider is illus-
trated in Fig. 3. The inputs are as follows: (i) D is
the dataset given in Fig. 1(a), (ii) P
h
is the sensitive
itemsets given in Fig. 2(a), and (iii) ψ = 3. Fig. 3(a)
shows the sensitive itemset and values for the other
variables at each iteration of the inner loop. Fig. 3(b),
on the other hand, shows the step-by-step evolution of
D from its initial value to the released database D
′
.
i X Sup
X
SS
P
h
(T) T victim
1 acd 4 {acd, ad} acd a
2 acd 3 {acd, ad} acde a
3 ad 4 {ad} abd a
4 ad 3 {a} acdh a
5 bcd 3 {bcd} bcde b
(a) Variables at each iteration
D After ith deletion D
′
i=1 i=2 i=3 i=4 i=5
abd abd abd bd bd bd
acd cd cd cd cd cd
abcg abcg abcg abcg abcg abcg
acde acde cde cde cde cde
acdh acdh acdh acdh cdh cdh
bcde bcde bcde bcde bcde cde
abcde abcde abcde abcde abcde abcde
abdfg abdfg abdfg abdfg abdfg abdfg
bcdfh bcdfh bcdfh bcdfh bcdfh bcdfh
(b) Step-by-step sanitization
Figure 3: The operation of BalancedHider for sanitizing the
sensitive itemsets (Fig. 2(a)) from the sample database (ψ =
3). (a) value of variables at each iteration (i) of the inner
loop, (b) step-by-step sanitization.
A TRADEOFF BALANCING ALGORITHM FOR HIDING SENSITIVE FREQUENT ITEMSETS
203
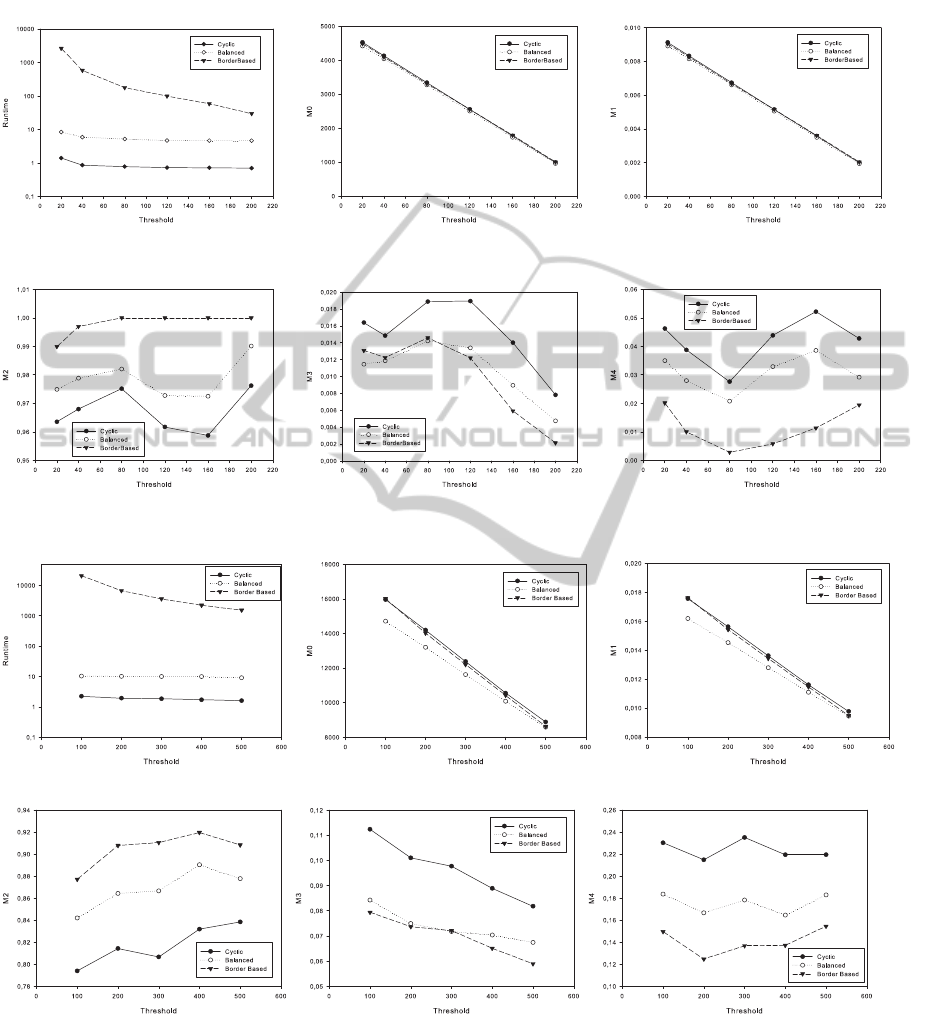
(a) Runtime (b) M0 (c) M1
(d) M2 (e) M3 (f) M4
(g) Runtime (h) M0 (i) M1
(j) M2 (k) M3 (l) M4
Figure 4: Sanitization results: [a-f] for
T10.I4.50K
, and [g-l] for
Retail
.
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
204

4 PERFORMANCE EVALUATION
In this section, we present the performance of Bal-
ancedHider and compare it to that of CyclicHider
and BBHider. The test computer used was equipped
with Intel Core2Duo 3.0Ghz processor, 2GB of main
memory and running Windows XP64 operating sys-
tem. For performance evaluation, a synthetic dataset
was generated using IBM synthetic dataset generator,
namely
T10.I4.50K
. We also used a real world mar-
ket basket database
Retail
(Brijs et al., 1999) from
FIMI repository.
Retail
contains 88163 transactions,
16470 different items, and 13 items per transaction on
average. For each of the two databases, 20 sensitive
frequent itemsets were selected somewhat arbitrarily,
and each sensitive itemset contains either two or three
items. Average support of sensitive itemsets are 249.8
for
T10.I4.50K
, 977.95 for
Retail
.
We always use runtime as the only efficiency met-
ric and use five different (M0 through M4) effec-
tiveness metrics to measure the distortion as follows.
Note that all the metrics except M2 have the ’the
smaller is the better’ property, and vice versa for M2.
• Runtime (in seconds): It equals to the completion
time.
• Data Dist. (M0): It equals to
∑
T∈D
|T| −
∑
T∈D
′ |T|.
• Information Loss (M1) (Oliveira and Za¨ıane,
2003) : It equals to
∑
i∈I
sup
D
({i})−sup
D
′
({i})
∑
i∈I
sup
D
({i})
.
• Quality (M2): It equals to
F
(
D
′
,ψ
)
|
F
(D,ψ)
−P
h
|
.
• Freq. Support Dist. (M3) (Abul et al., 2007b): It
equals to
1
F
(
D
′
,ψ
)
∑
X∈F
(
D
′
,ψ
)
sup
D
(X)−sup
D
′
(X)
sup
D
(X)
.
• Freq. Pattern Dist. (M4) (Abul et al., 2007b): It
equals to
|
F
(D,ψ)
|
−
F
(
D
′
,ψ
)
|
F
(D,ψ)
|
.
The results are plotted in Fig. 4. The results,
in summary, show that the effectiveness performance
of BalancedHider ranges between that of CyclicHider
and BBHider and efficiency performance is close to
that of CyclicHider.
5 CONCLUSIONS
In this work, we introduced a new algorithm for
sensitive frequent itemset hiding problem, which
aimed at finding solutions balancing the effi-
ciency/effectiveness tradeoff. The motivation was
built on our analysis that there is a big efficiency gap
between simple and sophisticated algorithms while
that of the effectiveness gap is relatively small. The
experimental results on two datasets confirm that the
algorithm indeed achieved its design criteria.
Our algorithm is very practical, making it useful
in many domains like online database publishing. Our
future work will include extension of the algorithm to
other knowledge formats.
ACKNOWLEDGEMENTS
The work is supported by TUBITAK under the grant
number 108E016.
REFERENCES
Abul, O., Atzori, M., Bonchi, F., and Giannotti, F. (2007a).
Hiding sensitive trajectory patterns. In 6th Int. Work-
shop on Privacy Aspects of Data Mining (PADM’07).
Abul, O., Atzori, M., Bonchi, F., and Giannotti, F. (2007b).
Hiding sequences. In Third ICDE Int. Workshop on
Privacy Data Management (PDM’07).
Abul, O., G¨okc¸e, H., and S¸engez, Y. (2009). Frequent item-
sets hiding: A performance evaluation framework. In
ISCIS’09.
Agrawal, R., Imielienski, T., and Swami, A. (1993). Min-
ing association rules between sets of items in large
databases. In SIGMOD ’93, pages 207–216.
Atallah, M., Bertino, E., Elmagarmid, A., Ibrahim, M., and
Verykios, V. S. (1999). Disclosure limitation of sensi-
tive rules. In KDEX’99, pages 45–52.
Brijs, T., Swinnen, G., Vanhoof, K., and Wets, G. (1999).
Using association rules for product assortment deci-
sions: A case study. In Knowledge Discovery and
Data Mining, pages 254–260.
Lee, G., Chang, C.-Y., and Chen, A. L. P. (2004). Hid-
ing sensitive patterns in association rules mining. In
COMPSAC’04.
Moustakides, G. V. and Verykios, V. S. (2006). A max-min
approach for hiding frequent itemsets. In ICDM’06.
O’Leary, D. E. (1991). Knowledge discovery as a threat
to database security. In Piatetsky-Shapiro, G. and
Frawley, W. J., editors, Knowledge Discovery in
Databases, pages 507–516. AAAI/MIT Press.
Oliveira, S. R. M. and Za¨ıane, O. R. (2003). Protecting sen-
sitive knowledge by data sanitization. In ICDM’03.
Sun, X. and Yu, P. S. (2005). A border-based approach for
hiding sensitive frequent itemsets. In ICDM’05.
Verykios, V. S., Elmagarmid, A. K., Bertino, E., Saygin, Y.,
and Dasseni, E. (2004). Association rule hiding. IEEE
TKDE, 16/4:434–447.
Weng, C.-C., Chen, S.-T., and Chang, Y.-C. (2007). A novel
algorithm for hiding sensitive frequent itemsets. In
ISIS’07.
A TRADEOFF BALANCING ALGORITHM FOR HIDING SENSITIVE FREQUENT ITEMSETS
205
