MODELING EDUCATIONAL KNOWLEDGE

Supporting the Collaboration of Computer Science Teachers

Peter Hubwieser and Marcus Bitzl

Fakultät für Informatik, Technische Universität München, Garching, Germany

Keywords: Ontology, Design of Lessons, Computer Science Education.

Abstract: The planning of lessons and courses is a very complicated work. Unfortunately many teachers tend to pre-

pare their lessons without profiting from the experiences of their colleagues. In this paper we show how the

collaboration of teachers could be supported by a community software that supports the collaboration focus-

ing on the knowledge elements that form the topic of the lesson that is to prepare. Starting from the didac-

tical model of Heimann, Otto and Schulz, we have designed an ontology that comprises most of the infor-

mation that is necessary to design a lesson in computer science.

1 INTRODUCTION

Every teaching person has to realize that the concep-

tual design of courses and lessons is a very compli-

cated and difficult task. There is a large variety of

influencing factors that have to be considered and

many decisions have to be made. It is nearly imposs-

ible to keep all these circumstances in mind while

designing a course of lessons. Thus teachers tend to

make many of these decisions more from the heart

than based on rational deliberations.

On the other hand it would be very helpful for a

teacher if she/he could share the experiences that

other colleagues have made with similar topics. To

this purpose the teachers would have to describe all

the circumstances of these experiences very closely,

which might be quite annoying. In order to enhance

the exchange of experiences between teachers, the

information from other colleagues would have to be

presented “just in time”, exactly at the point of a

specific lesson planning process where it is needed

and only in the case that most of the circumstances

are similar. This requires a theoretical framework

that offers suitable structures and categories on the

one hand as well as properly defined terms, concepts

and notions on the other, allowing to describe a

specific teaching situation as precisely as possible.

After many years of deliberations about semantic

systems that might support the collaboration of

teachers (Hubwieser and Schlichter, 1998), based on

the experiences we have made during the design and

implementation of a new mandatory subject of in-

formatics in Bavarian secondary schools (Hubwies-

er, 2006) and stimulated by the rapid evolution of

the semantic web, we have developed an ontology

that is based on the Berlin Model, which was one of

the first rational decision-making models that was

suitable for everyday teaching (Uljens, 1997). Addi-

tionally we integrated three different (so far quite

separate) theories, as described already by Staller

(2006): (1) Prerequisite analysis of Instructional

design following Smith and Ragan (2005), (2) two

taxonomies of learning objectives (Anderson and

Krathwohl, 2001, Fuller et al., 2007), and (3) the

ACM Computing ontology (Cassel et al., 2007).

The final goal of our research process is to de-

velop a software system (called PrepSpace) that

supports teachers in the collaborative design of

courses and lessons. Besides that, there are many

other application areas of our ontology as well, e.g.

the retrieval of teaching materials, the design and

automatic evaluation of student assessments, the

comparison of courses of lessons.

Meanwhile our ontology has become quite stable

and PrepSpace has reached the first prototype state,

thus we decided to publish the state of our work

right now in order to put it up for discussion.

229

Hubwieser P. and Bitzl M..

MODELING EDUCATIONAL KNOWLEDGE - Supporting the Collaboration of Computer Science Teachers.

DOI: 10.5220/0003088602290234

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 229-234

ISBN: 978-989-8425-29-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

2 THEORETICAL

BACKGROUND

2.1 The Berlin Model

The Berlin Model was developed by Heimann, Otto

and Schulz, see Uljens (1997). We have chosen this

model as the theoretical framework for the teacher

education courses in informatics at the Technische

Universität München (Brinda and Hubwieser, 2009).

Following the Berlin model the design of educa-

tional lessons has to start with the consideration of

the preconditions in two different areas: firstly the

socio-cultural preconditions, which comprise e.g.

the legal requirements for school education, didactic

approaches as well as IT infrastructures in schools.

Secondly, the anthropogenic preconditions describe

the attributes of the students like age, gender, prere-

quisite knowledge or social status.

In a second step the teacher has to make his/her

decisions about the four main aspects of a lesson:

intentions, content, methods and media.

Finally the consequences of the course or the les-

son have to be considered, regarding the (anthropo-

genic) learning progress of the students as well as

more global (socio-cultural) consequences like the

improvement of the educational level of a region or

of the whole country.

Our system is designed to support this strategy of

planning by a maximum of information that is of-

fered to the teacher exactly at the right time he/she

needs it during the design process.

2.2 Learning Objectives

We will refer to the definition of (Smith and Ragan,

2005, p. 96): “A learning objective is a statement

that tells what learners should be able to do when

they have completed a segment of instruction.”

Concerning the granularity of the objectives,

(Anderson and Krathwohl, 2001, p. 15f) suggest

three categories:

− Global Objectives: “Complex, multifaceted learn-

ing outcomes that require substantial time and in-

struction to accomplish;”

− Educational Objectives: derived from global

objectives by breaking “them down into a more

focused, delimited form;”

− Instructional Objectives, with the purpose “to

focus teaching and testing on narrow, day-to-day

slices of learning in fairly specific content areas.”

2.3 Taxonomies

Our starting point was the the taxonomy of Ander-

son and Krathwohl (2001), shortly called AK from

now on. Following AK, we regard learning objec-

tives as a combination of a certain type of knowledge

and an observable behavior specification (called

cognitive process) concerning this type of know-

ledge, together forming the two dimensions of the

AK-Taxonomy:

(1) The knowledge dimension is partitioned into A.

factual, B. conceptual, C. procedural, and D. meta-

cognitive knowledge,

(2) the cognitive process dimension contains the

following levels of behavior: 1. remember, 2. under-

stand, 3. apply, 4. analyze, 5. evaluate, and 6.

create.

A certain cell of the AK-taxonomy is specified by a

combination of a letter (for the knowledge dimen-

sion) and a digit (for the cognitive process dimen-

sion), e.g.: A1, B3, D6 (see figure 1).

Recently a working group of the ACM Special

Interest Group on Computer Science Education

(SIGCSE) elaborated a specific taxonomy for com-

puter science (Fuller et al., 2007), which splits the

cognitive process dimension of the AK-taxonomy

into the two subdimensions producing and interpret-

ing. The producing subdimension represents the

more active part of the learning process and contains

the steps none, apply, and create. The remaining

activities of the cognitive process dimension are

arranged on the interpreting subdimension: remem-

ber, understand, analyze, evaluate. This results (in

combination with the knowledge dimension) in a

three-dimensional taxonomy, which we will shortly

call SIGCSE-taxonomy.

2.4 Learning Objective Analysis

In order to illustrate our theoretical considerations

through this paper, we present an exemplary learn-

ing process P1, specified by a “final examination”

task T1. Once the students have finished P1, they

should be able to solve the following task T1:

Write a method of a suitable Java class that calcu-

lates and prints (on screen) the values of a square

function f(x) = ax

+ bx + c for a given set of equi-

distant arguments {x

, ..., x

}. The following parame-

ters should be set by the user of the program:

− a, b, c: double (parameters of the function f),

− x_min, x_max: double (borders of the x values),

− n: int (number of arguments x

to calculate f(x

)).

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

230

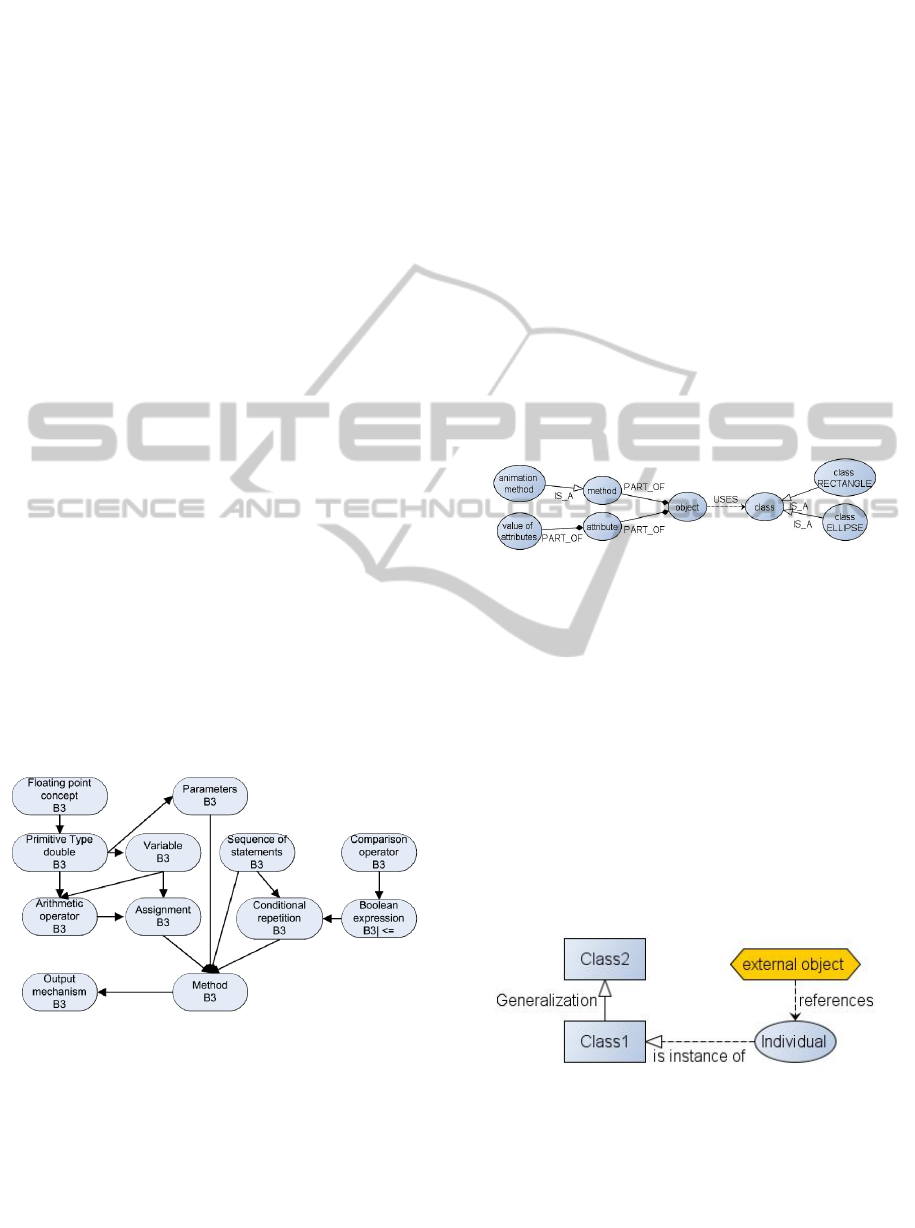
The students have to learn certain knowledge ele-

ments in order to solve this task. Some of them are

shown in the graph of the learning objectives in

figure 1, represented by the denominators of the

learning objectives, e.g. “conditional repetition”).

Additionally the corresponding cell of the AK-

taxonomy is indicated at the lower end of the nodes.

2.5 Prerequisite Relations

The prerequisite analysis of learning steps is a very

important part of the instructional design process, as

described by Smith and Ragan (2005). Although the

prerequisite concept is not suitable to enhance con-

structivistic learning, obviously many situations in

educational work and research require such an anal-

ysis.

We transfer the concept of prerequisite analysis

to sets of learning objectives in order to find prere-

quisite relations. We regard a prerequisite relation P

as a set of pairs of learning objectives:

P = {(O1, O2)| O1 is prerequisite of O2}. Instead of

(O1, O2) ∈ P, we shortly write P: O1 → O2.

As pointed out in (Hubwieser, 2008), we suggest

two different types (PH, PS) of prerequisite relations

that might connect learning objectives in pairs O1,

O2:

The hard prerequisite relation (PH) is forced by a

substantial or logical dependency, e.g.: concept2

contained in objective O2 is logically based on con-

cept1 contained in objective O1. This means that it

is not possible to understand concept2 without hav-

ing understood concept1.

Figure 1: Prerequisite structure of task T1.

The soft prerequisite relation (PS) is suggested by

didactical deliberations: It is not necessary, but ad-

visable to reach objective O1 in order to ease or to

improve the learning process towards O2, e.g. to

apply teaching or working methods that support

didactical principles.

Whereas PH often can be derived from logical rela-

tions, PS needs empirical research. Using learning

objectives as nodes and prerequisite relations as

edges, we can draw prerequisite graphs representing

PH or PS or a combination of both. In this paper we

will restrict our deliberations to PH. Applied to our

example of the task T1, this leads to the prerequisite

graph that is shown in figure 1.

2.6 Subject Domain Knowledge

The most important aspect of the design of courses

is the description of the knowledge that the students

should gain during the lessons. We decided to

represent it in the form of knowledge elements

(shortly KE), similar to the proposal of Pedroni and

Meyer (2010). The granularity of these KEs should

be approximately about the learning content of one

single lesson.

Figure 2: Knowledge elements in grade 6.

The knowledge elements are connected by associa-

tions that are induced by the logical structure of the

subject domain. The ACM Computing Ontology

(Cassel et al., 2007) proposed the following associa-

tions: is_a (generalization), part_of (aggregation)

and uses (unspecified relationship). Figure 2 shows

(partly) the result of a curriculum analysis of grade 6

of the subject of informatics in Bavaria, using these

associations.

3 THE ONTOLOGY

Figure 3: Notation of the following figures.

The following figures 4 and 5, that show parts of the

ontology, are drawn manually (using the graphic

editor yEd) in order to produce more readable fig-

ures compared with Protege plugins like Jambalaya.

MODELING EDUCATIONAL KNOWLEDGE - Supporting the Collaboration of Computer Science Teachers

231

Additionally we have simplified the graph in some

parts by restricting ourselves to some exemplary

individuals and properties.

The core part of the ontology of PrepSpace is

dedicated to the concepts that are the most important

for the design of courses and lessons (see figure 4):



learning objectives, connected by prerequisite

relations,



subject domain knowledge elements, con-

nected by the associations is_a, part_of, uses

(especially implements).

Figure 4: The central area of the ontology.

The lesson to be planned is represented by an exter-

nal object (outside of the ontology), called learning

unit (LU). A second type of external objects is used

to represent the tasks that are designed to test the

intended learning objectives.

We represent our ontology using the Web Ontol-

ogy Language OWL 2.0. In order to operate on the

prerequisite graphs automatically, we have to per-

form logical reasoning on it, e.g. chaining a se-

quence of transitive relations or applying predicate

calculus. Thus we want our ontology to be decida-

ble, therefore we use OWL DL (Description Logics).

The external elements for tasks and learning

units are connected by the association has_context

with the application context of the course which

represents the most important preconditions follow-

ing the Berlin Model, e.g. grade, school type, sub-

ject, state or direction of study.

The cognitive process dimension of the AK-

taxonomy is implemented by a subclass hierarchy

following AK p. 67f (see figure 5). The extended

SIGCSE taxonomy is integrated in our system a

similar way. The implementation of the knowledge

dimension offers the docking slot for the subject

domain ontology, e.g. the ACM Computing Ontology

(Cassel et al., 2007). Similarly to the cognitive

process dimension, we constructed a hierarchy of

subclasses with the root class Knowledge that fol-

lows the major types and subtypes of the AK-

taxonomy (p. 46), see figure 5.

The remaining decision fields methods and me-

dia following the Berlin Model are covered by the

classes and individuals of the two areas Methodolo-

gy and Media in the ontology, which are connected

to the learning units by suitable properties (e.g.

has_media). These areas offer specific didactical

knowledge, e.g. proposals for teaching strategies like

team work or partner work or schemata for time

planning.

Figure 5: The knowledge dimension of the ontology.

Let us assume that a certain teacher aims to enable

her/his students to solve the task T1 that is described

above (see 2.4). She/he might specify the following

learning objective for the lesson: “apply the method

concept in an object oriented programming lan-

guage”. We regard this as an instructional objective,

belonging to the cell B3 following AK. In the case

that our ontology contains the information shown in

figure 1, the reasoner (we use HermiT, see Motik,

Shearer, Horrocks (2009)) will produce a tree of

prerequisite objectives that might look as (partly)

shown in figure 6.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

232

To describe these general dependencies between

knowledge elements we define an object property

has_dependency with is_a, has_part (inverse of

part_of), uses and implements as its subproperties.

Figure 6: Part of the prerequisite tree.

As we are interested in dependencies between learn-

ing objectives, we can define the PH

has_direct_prerequisite as follows:

SubObjectPropertyOf(

ObjectPropertyChain(

:has_knowledge :has_direct_dependecy

:has_objective)

:has_direct_prerequisite)

Often one is interested in the overall dependen-

cies of a learning object (e.g. what has a student

learned if he has reached this learning object?). This

is a more general case than direct dependencies:

SubObjectPropertyOf(

:has_direct_prerequisite

:has_prerequisite

)

Further, general dependencies without restric-

tions to the next dependent learning objective are

transitive:

TransitiveObjectProperty(

:has_prerequisite ).

4 USE CASE

Let us assume that a teacher wants to prepare her/his

lesson following the Berlin Model. Thus, the prepa-

ration will start with the consideration of the pre-

condition areas. We will support some of them by

offering a specific part of the ontology for the con-

text of a lesson: grade, school type, teaching subject,

state/country and direction of study.

Now the decisions concerning the four areas in-

tentions, content, methods and media have to be

made. All these decisions are connected to the (ex-

ternal) LU-object by references to the corresponding

objects of the ontology, e.g. to learning objectives.

Regarding the content decision, the teachers will

start to use our system by picking certain knowledge

elements (KE) that represent the central topics of the

lesson. PrepSpace will be able to present a certain

part of the graph of the subject domain knowledge

that surrounds the picked KE, showing all the other

KEs that are linked to the concerned one by one of

the properties is_a, part_of or uses. By this way the

teacher is able to inspect the knowledge area that is

relevant to the intended learning process.

The next step might be to specify the intention of

the lesson by fixing the learning objects the students

should achieve by adding a cognitive process opera-

tor to the KE, e.g. explain. PrepSpace will present a

prerequisite graph of learning objectives, enabling

the teacher to assess quite precisely, which objec-

tives the students have to achieve before the in-

tended learning step might take place.

After exploring the knowledge and objectives of

the intended lesson, the teacher starts to think about

the teaching methods, strategies and media she/he

wants to apply in the lesson. As much didactical

knowledge about these areas is represented in Prep-

Space, the teacher can get many hints and proposals

directly from the system. This is the point where the

user will profit mainly from the collaboration with

other teachers that is mediated by PrepSpace. The

teacher might look in the (web based) system after

the methods or media that other teachers have used

(and assessed) in lessons to the same KE or similar

learning objectives.

5 RELATED WORK

In their prophetic paper Mizoguchi and Bourdeau

(2000) proposed a framework for ontology-based

intelligent systems and elaborated a roadmap to this

goal. This proposal triggered a lively discussion

about educational ontologies and intelligent systems

that were built upon these, which was particularly

productive at the workshops of the SW-EL (Applica-

tions of Semantic Web technologies for E-Learning)

series.

The heavy-weight OMNIBUS ontology (Mizo-

guchi, Hayashi, Bourdeau, 2007) is built to support

all the concepts necessary for understanding learn-

ing, instruction and instructional design. For our

purpose it is too general on the one hand, but misses

the close description of the subject domain know-

ledge structure and of the learning objectives on the

other hand. Dicheva, Sosnovsky, Gavrilova, Brusi-

MODELING EDUCATIONAL KNOWLEDGE - Supporting the Collaboration of Computer Science Teachers

233

lovsky (2005) produced an ontological overview of

the Ontologies for Education field and offer an on-

tology-driven web portal in order to compare and

combine different proposals for educational ontolo-

gies.

Pedroni and Meyer (2010) have developed the

concept of trucs (testable, reusable units of cogni-

tion) to describe knowledge elements and their de-

pendencies.

Kasai and Yamaguchi (2005) presented a Seman-

tic Web System for helping teachers plan lessons

that is based on some specific ontologies, particu-

larly on a goal ontology.

Recently an ACM SIGCSE working group (Cas-

sel et al., 2007) continued the ongoing work on the

ACM Ontology of Computing and proposed a new

ontology that served as a starting point of our con-

siderations concerning the subject domain area of

learning processes.

6 FUTURE WORK

Currently we are preparing a close empirical survey

on how teachers prepare their lessons. After devel-

oping a questionnaire based on expert interviews, we

will perform a survey using this questionnaire,

searching for different types of preparation strate-

gies. Finally we will adopt our tool to the results of

this study, before we will roll it out for public usage.

Further we prepare to use the ontology as well to

manage research results that concern learning paths,

learning difficulties or the comparison of different

teaching approaches for the same knowledge ele-

ment.

REFERENCES

Anderson, L. W., & Krathwohl, D. R. (2001). A taxonomy

for learning, teaching, and assessing: A revision of

Bloom's taxonomy of educational objectives. New

York: Longman.

Brinda, T., & Hubwieser, P. (2010). How to teach didac-

tics of informatics to informatics student teachers. In

IFIP (Ed.), New developments in ICT and Informatics

education. To appear.

Cassel, L. N., Davies, G., Fone, W., Hacquebard, A.,

Impagliazzo, J., LeBlanc, R., … (2007). The compu-

ting ontology: application in education. In ITiCSE-

WGR ‘07: Working group reports on ITiCSE on Inno-

vation and technology in computer science education

(pp. 171-183). New York, NY: ACM.

Dicheva, D., Sosnovsky, S., Gavrilova, T., & Brusilovsky,

P. (2005). Ontological Web Portal for Educational On-

tologies. In L. Aroyo & D. Dicheva (Eds.), SW-

EL’05: Applications of Semantic Web Technologies

for E-Learning. (pp. 19–28). Amsterdam.

Fuller, U., Johnson, C. G., Ahoniemi, T., Cukierman, D.,

Hernán-Losada, I., Jackova, J., (2007). Developing a

computer science-specific learning taxonomy. SIGCSE

Bull., 39(4), 152-170.

Hubwieser, P. (2006). Functions, Objects and States:

Teaching Informatics in Secondary Schools: Invited

talk. In R. Mittermeir (Ed.): Informatics Education -

The Bridge between Using and Understanding Com-

puters (pp. 104-116). Berlin: Springer.

Hubwieser, P. (2008). Analysis of Learning Objectives in

Object Oriented Programming. In R. T. Mittermeir &

M. M. Syslo (Eds.): Informatics Education - Support-

ing Computational Thinking (pp. 142–150). Berlin:

Springer.

Hubwieser, P., & Schlichter, J. (1998). HyperCons: Inte-

grating and structuring school relevant information on

the internet. In C. L. Fulmer, B.-Z. Barta, & P. Nolan

(Eds.), The Integration of Information for Educational

Management. Whitefield, MN: Felicity Press.

Kasai, T., & Yamaguchi, H. (2005). A Semantic Web

System for Helping Teachers Plan Lessons Using On-

tology Alignment. In L. Aroyo & D. Dicheva (Eds.),

SW-EL’05: Applications of Semantic Web Technolo-

gies for E-Learning. (pp. 9–17). Amsterdam.

Mizoguchi, R., & Bourdeau, J. (2000). Using Ontological

Engineering to Overcome Common AI-ED Problems.

International Journal of Artificial Intelligence in Edu-

cation, 11(2), 107–121.

Mizoguchi, R., Hayashi, Y., & Bourdeau, J. (2007). Inside

Theory-Aware and Standards-Compliant Authoring

System. In D. Dicheva, R. Mizoguchi, N. Capuano, &

A. Harrer (Eds.), SWEL’07: Ontologies and Semantic

Web Services for Intelligent Distributed Educational

Systems. (pp. 1–18). Marina del Rey, CA.

Motik, B., Shearer, R., & Horrocks, I. (2009). Hypertab-

leau Reasoning for Description Logics. Journal of Ar-

tificial Intelligence Research, 36, 165–228.

Pedroni, M., & Meyer, B. (2010). Object-Oriented Model-

ing of Object-Oriented Concepts. In J. Hromkovic, R.

Královic, & J. Vahrenhold (Eds.): Teaching funda-

mental concepts of informatics. (pp. 155–169). Berlin:

Springer.

Smith, P. L., & Ragan, T. J. (2005). Instructional design

(3. ed.). Hoboken, NJ: Wiley.

Uljens, M. (1997). School didactics and learning: A school

didactic model framing an analysis of pedagogical im-

plications of learning theory. Hove: Psychology Press.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

234