PURE CO-EVOLUTION FOR SHAPE NESTING

Jeffrey Horn

Mathematics and Computer Science, Northern Michigan University

1401 Presque Isle Avenue, Marquette, Michigan, U.S.A.

Keywords: Shape nesting, Coevolution, Co-evolution, Cooperation, Cooperative Co-evolution, Fitness sharing,

Resource-defined fitness sharing, Speciation, Niching, Selection, Infinite population.

Abstract: We test the effectiveness of an evolutionary algorithm that relies completely on species selection for

evolution and on interactions among species to determine fitness. Under Resource-defined Fitness Sharing

(RFS), all individuals have the same objective fitness, but they act to reduce their shared fitness through

competition for resources. In previous studies, RFS has been used to evolve populations of mutually non-

competing (i.e., non-overlapping) shapes on shape nesting problems. In this paper we test the effectiveness

of a modified version of RFS, which we call PCSN, against three commercial software packages for shape

nesting. PCSN uses species proportions to represent a population, thereby simulating an infinitely large

population. With no discovery operators, such as mutation or recombination, evolution consists of

selection only, with all species present in the initial population. We show that on some shape nesting

problems this approach can outperform some commercial packages. In particular, PCSN nests more circles

on a fixed, polygonal substrate than do most of the commercial packages. This might be considered a

surprising result, since the algorithm is radically different from any shape nesting algorithms deployed to

date. While conventional methods place one shape at a time, the co-evolution approach attempts to place

all shapes simultaneously.

1 INTRODUCTION

Recent work (Horn, 2002, 2005) on a co-

evolutionary approach to the shape nesting problem

has yielded intriguing results on various types of

shapes. The nestings “look good”. But to date the

resource-defined fitness sharing

(RFS) method has

not been directly compared to other algorithms. In

this paper we document the first such experiments,

in which a modified version of RFS is directly

compared to existing algorithms in the form of

commercial software packages. The results indicate

that this new approach is competitive with all three

packages, even outperforming two of them.

Our modifications to RFS attempt to bring out

the essential co-evolutionary aspects of the

algorithm, which we believe perform subset

selection on the set of species (i.e., unique

individuals) present in the initial population, seeking

the “optimal” subset. To focus on these aspects of

co-evolution, we remove all discovery operators

US Patent No. 7181702.

(e.g., mutation and recombination), relying solely on

selection. We remove individuals from the

population representation, and replace them with

species proportions, implying an infinitely large

population. We call this Pure Co-evolutionary

Shape Nesting, or PCSN.

2 BACKGROUND

We discuss the shape nesting problem domain and

the application of the RFS approach to it.

2.1 The Shape Nesting Problem

The general problem at hand involves “nesting”

(that is, placing) shaped pieces on a finite substrate

so as to maximize the number of such pieces on the

substrate. The objective is often stated, equivalently,

as the minimization of “trim” (i.e., unused substrate)

(Dighe and Jakiela, 1996; Kendall, 2000). No

overlaps among the placed pieces are allowed, and

all such pieces must be placed so as to be completely

255

Horn J..

PURE CO-EVOLUTION FOR SHAPE NESTING.

DOI: 10.5220/0003089402550260

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 255-260

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

within the boundaries of the substrate. Figure 1

depicts a nesting of polygons within a polygon.

Shape nesting problems arise in a number of

industries, such as automotive manufacturing, in

which various shaped parts must be stamped from

sheet metal substrate, and the garment industry,

where component apparel pieces must be cut from

bolts of cloth (Kendall, 2000).

Here we assume a finite, two-dimensional

problem: a flat substrate of fixed size, and flat pieces

to be nested. We assume identical shape: there is

only one shape we are nesting. We limit ourselves to

arbitrary, (possibly non-convex) polygons for the

substrate and to identical circles for the shaped

pieces to be nested. These limitations help to reduce

the number of parameters to vary in each algorithm

when we run comparison tests, which is the main

focus of this paper.

2.2 Previous Work

Horn (2002) applied RFS to one and two-

dimensional shape nesting problems but limited his

tests to axis-aligned squares for the shaped pieces.

Horn (2005) extended the 2002 results by applying

RFS to arbitrarily shaped polygons, for both the

substrate and for the pieces to be nested. Figure 1

shows one of the nesting problems, along with one

nesting found by RFS, from the 2005 paper. More

recent work on RFS is of a theoretical nature (Horn,

2008).

Figure 1: General polygon nesting (Horn, 2005).

2.3 The RFS Algorithm

The implementation of resource-defined

fitnesssharing on which we base PCSN is the same

as used by Horn (2002, 2005).

2.3.1 Encoding the Decision Variables

For the two dimensional shape nesting problem, the

placement of a piece is made by specifying the

piece’s location and its orientation (rotation).

Because we are nesting circles in the current paper,

we only have to specify location, which will be an

(x,y) coordinate in the Cartesian plane.

2.3.2 RFS Selection

Every individual of the current population is

evaluated and assigned a fitness. As with Horn

(2002, 2005), chromosomes that specify a placement

of a piece that extends beyond the boundaries of the

substrate are assigned a fitness of 0. All “feasible”

individuals (i.e., chromosomes specifying piece

placements entirely on the substrate), receive fitness

greater than 0.

For each of the feasible individuals we compute

a shared fitness (Goldberg and Richardson, 1987)

for use in a standard selection method. In RFS, the

shared fitness for each individual is a function of the

area of the individual piece, its placement on the

substrate, and the extent to which the placed piece

overlaps with other placed pieces.

To describe the selection mechanism more

specifically, we need to define terms. Figure 2

illustrates the terms for two overlapping shaped

pieces a and b. The area of the shaped piece, which

is identical for all individuals in the population, is

used as the objective fitness of each individual: f

= f

for all shaped pieces i. The area of

overlap between pieces a and b is defined as f

, so

that 0 ≤ f

≤ f

. Overlap is symmetric: f

Figure 2: RFS terms with non-convex polygons.

Next we define what we mean by species and

how they relate to individuals. In (Horn, 2002,

2005) the population consists of individuals. An

individual is simply a member of the population.

Two individuals from the current population may

have the exact same alleles on their chromosomes,

( = f

)

ICEC 2010 - International Conference on Evolutionary Computation

256

yet they occupy different “slots” in the population

(e.g., different elements of the data structure holding

the population) and so represent distinct individuals.

A species is considered to be a set of identical

individuals (i.e., with identical placements). Thus

unique chromosomes (x,y) map one-to-one with

unique species. There is complete overlap between,

and only between, any two members of the same

species.

Now we can give the specific form of the RFS

shared fitness f

Sh,k

calculation:







species Y

Sh,X

Sh,i

XYY

The upper and lower equations above are

equivalent. Both have an objective fitness in the

numerator, and a niche count, calculated over the

entire current population, in the denominator. In

Equation 1a, the summation in the niche count is

taken over the population of individuals (using the

variable h). In Equation 1b, the population is divided

into species Y. Each species consists of the set of all

individuals with the same chromosomes (from the

current population). Thus the shared fitness for any

member of a species X is equal to the objective

fitness of that species divided by the niche count for

that species, which is computed as the sum over all

species of the interaction term (f

) multiplied by the

number of members in that species, n

. For example,

the RFS shared fitness calculation for the two

species A, B in Figure 2 (corresponding to the two

individuals a and b respectively) would be

AB B

AB A

fnfn

Sh,B

Sh,A









(2)

3 THE PCSN ALGORITHM

In this paper we choose to implement the RFS

approach a bit differently to take advantage of what

we perceive as the true strengths of this type of co-

evolution.

The previous section describes a more traditional

implementation in which a population of individuals

undergoes selection, mutation, and recombination.

But as noted there and in (Horn, 2008), it seems that

the RFS type of co-evolutionary selection operates

on species, as defined above. Furthermore, it seems

to be able to handle very large numbers of

individuals and species, so that we might be able to

rely on a large initial population for diversity, rather

than on discovery operators such as mutation and

crossover.

Therefore in the approach taken here, which we

call pure co-evolutionary shape nesting (PCSN), we

will (1) implement the infinite population model

(usually used for theoretical studies of an

evolutionary algorithm), dealing only with species,

not individuals, and (2) use selection only, omitting

all forms of mutation and recombination.

We maintain a population of species. For each

species we keep track of the proportion of the

population claimed by the species at a particular

generation. (Note that each species corresponds to a

unique piece placement, in this case an x,y

coordinate for a circle, as describe in the previous

section.) We apply proportionate selection to obtain

the expected proportion of the population for each

species in the following generation. Thus we model

an infinite population, at least to the extent of the

precision in our computer representation of a species

proportion.

Specifically, let p

(t) be the proportion of species

x at time (generation) t. Then under proportionate

selection, the expected proportion of x at time t+1 is

given by:

(3)

where f

sh,x

(t) is the shared fitness of species x at time

t, as described in the previous section. For PCSN,

we use this equation to compute the next generation.

(In generation 0, we initialize the population of

species to equal proportions).

4 EXPERIMENTS

We compare PCSN with existing implementations

of “mature” shape nesting algorithms, to get some

idea if this new approach has potential for practical

application. First we discuss the problem at hand.

(1a)

(1b)

PURE CO-EVOLUTION FOR SHAPE NESTING

257

4.1 A Nesting Problem

We consider non-convex polygon P1 defined in

Table 1. (Note that depictions of P1 in this paper

assume the origin is in the upper left corner, so that

the y-axis values increase down the page, while x-

axis values increase to the right.) The shape to be

nested is a circle of radius 72.

Table 1: Polygon P1.

(x,y) coordinates for fourteen vertices

in clockwise order of visitation

(0,56), (110,0), (254,0), (356,175), (476,142), (644,98),

(770,128), (770,196), (742,309), (619,406), (500,363),

(363,421), (350,509), (309,645), (127,673), (55,533),

(56,372).

We compare three commercial software

packages with each other and with RFS-based Pure

Co-evolutionary Shape Nesting (PCSN) on P1.

4.2 Three Software Packages

We apply the demonstration/trial versions of three

commercially available software packages that

include a shape nesting tool. All three, as well as the

PCSN program, are run on the same machine, a

Lenovo R61 laptop with a dual-core 1.8 GHz

processor and 2 GB of main memory. The three

packages are listed in Table 2.

Table 2: Commercial shape nesting software used.

Package

Name

Version Company Web Site

ArtCAM

Insignia

3.000k Delcam Plc www.artcam.com/

ProNest

8.2.1.1

MTC

Software

www.mtc-

software.com

OptiNest

2.3.1

Boole &

Partners

www.boole.eu

4.3 PCSN Setup

All runs of the PCSN algorithm use a diversity

setting of 6000 species. The species are generated at

random by drawing a minimum size bounding

rectangle around P1 and then generating integer

coordinates x and y independently and uniformly at

random within the bounding rectangle, discarding

duplicates and infeasibles (those coordinates which

would center a circle outside of P1 or intersecting a

side of P1), until 6000 unique and feasible

coordinates are found. Selection is then iterated once

per generation. Each generation we examine the set

of species whose proportion in the current

population exceeds 1/6000. When this set consists

entirely of non-overlapping circles, we stop the

algorithm and display that set of species.

4.4 Results

In this section we present separately the results of

running each of the shape nesting approaches:

PCSN and the three commercial packages, each

nesting the same shape, a circle of diameter 72 units,

in the same polygon (P1).

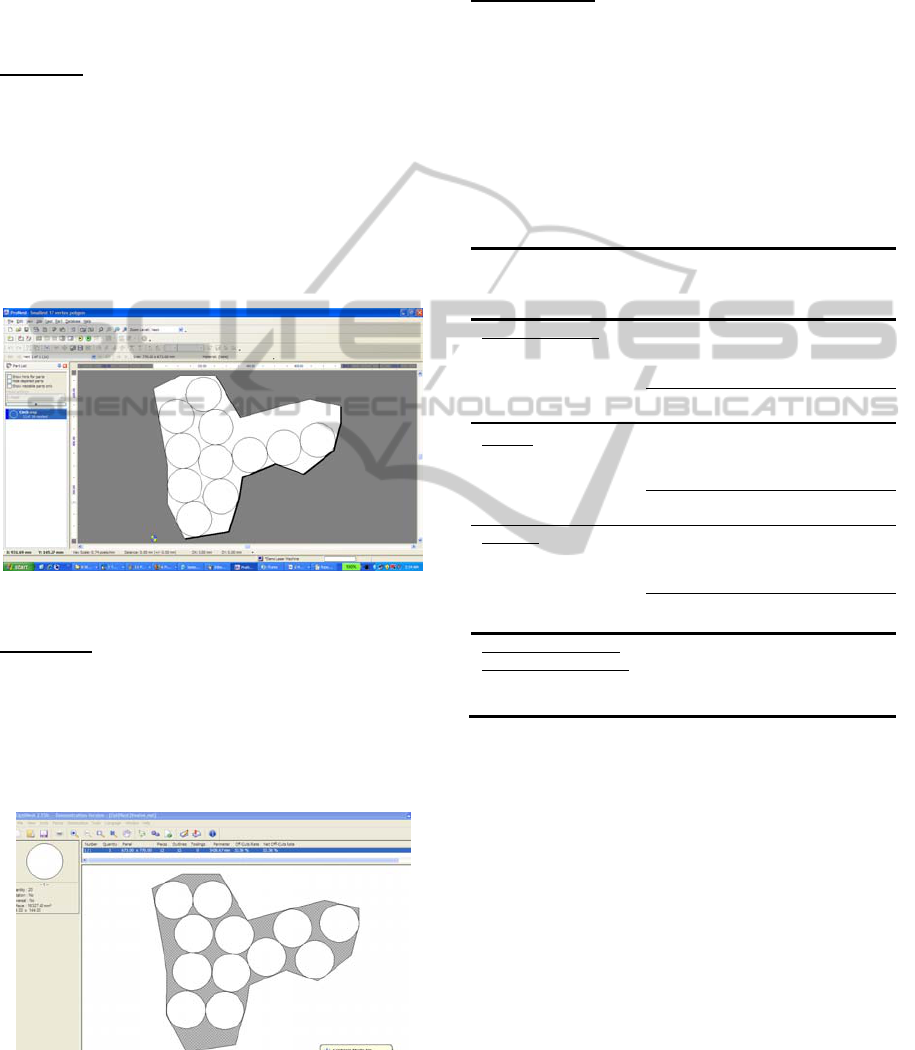
PSCN: Figure 3 shows that PCSN can nest 12

circles in P1.

Figure 3: PCSN fits 12 circles into P1.

Figure 4: ArtCAM nests 11 circles in P1.

ArtCAM: In Figure 4 we see the results of one run

of ArtCAM Insignia with a nesting of 11 circles.

ArtCAM’s nesting parameters require that the user

specifies which of four corners to use as the start of

nesting: upper left, upper right, lower left, and lower

ICEC 2010 - International Conference on Evolutionary Computation

258

right. A second, independent nesting parameter

specifies the direction of nesting (implying a

sequential algorithm): the x-direction or the y-

direction. This yields eight possible settings of

ArtCAM’s nesting parameters. We tried all eight,

and all eight yielded an eleven circle nesting.

ProNest: Unlike ArtCAM, ProNest has many

different nesting parameters with many possible

settings. We first tried ProNest on P1 using the

initial setting of parameters as they are found when

the program is started. This resulted in a nesting of

ten circles (not shown).

We next explored the range of possible nesting

parameter settings and settled on what appeared to

be an optimal setting, resulting in the eleven circle

nesting shown in Figure 5.

Figure 5: ProNest with optimized settings fits 11.

OptiNest: With OptiNest, there are also a large

number of nesting parameters to “tune”, some of

which are continuous-valued, resulting in an infinite

number of possible parameter combinations. So we

first tried a nesting using what OptiNest names the

“default settings”. The result was an eleven circle

nesting (not shown).

Figure 6: OptiNest with optimized settings fits 12.

By spending about thirty minutes exploring the

effects of various nesting parameters (e.g.,

“subgroup size”), we settled on what appears to be

the optimal performance for OptiNest on P1. Figure

6 shows the twelve circle nesting.

SUMMARY: Table 3 summarizes these results.

The numbers in bold are the best-seen-so-far, which

is twelve circles for P1, obtained by both the PCSN

and OptiNest with optimal parameter settings. Note

that the run times are approximate, and simply show

that all four approaches are similar in execution

time. In much of the literature on shape nesting

applications, a run time of several minutes or less is

considered acceptable.

Table 3: Results on Polygon P1.

Method or Package No. of circles

nested in P1

Approximate

Run Time

(seconds)

ArtCAM Insignia

(with initial settings)

(best of all runs)

11 60

ProNest

(with initial settings)

(best of all settings)

11 5

OptiNest

(with default settings)

(with optimized settings)

11 2

12 140

Pure Co-evolutionary

Shape Nesting (PCSN)

(with diversity 10000)

5 DISCUSSION

The modified version of RFS that we introduce as

PCSN (Pure Co-evolutionary Shape Nesting)

represents a population distribution as a vector of

species proportions, thus allowing the use of a

simple replicator equation to implement evolution.

The PCSN approach has a number of possible

advantages and disadvantages but this study is

meant only to introduce the approach.

The above results on polygon P1 provide

evidence that the co-evolutionary approach to shape

nesting can sometimes perform as well as, or better

than, existing, deployed algorithms (as sampled in

the current commercial software tested here). But

the application of the commercial software packages

PURE CO-EVOLUTION FOR SHAPE NESTING

259

was not performed by someone trained in the use of

such packages. For ProNest and OptiNest in

particular, the number of parameters to tune is quite

a high. A more rigorous study is in order, in which

parameter settings are explored in a systematic

manner. (On the other hand, the fact that commercial

packages require such parameter tuning, while

PCSN does not, can be considered a strength of

PCSN in particular, and of co-evolutionary

approaches in general.)

And yet PCSN does have one critical parameter:

its diversity setting. This corresponds to the “species

population size”, that is, the number of species

represented. How high should this be set for a

particular problem? Without discovery operators

such as mutation and crossover, even if PCSN can

scale to larger (i.e., more species) populations, it is

not clear that enough diversity can be generated this

way.

And larger, more challenging problems are out

there. Nesting circles, even inside of arbitrary

polygons, is not as impressive as nesting more

complex shapes, especially shapes that are not

rotationally symmetric. Also, the numbers of circles

nested in P1 are relatively small. Typical problems

in industry involve nesting dozens or even hundreds

of shapes on one substrate. Still, the fact that PCSN

is able to select subsets of a dozen or so shapes from

a set of thousands (e.g., 6000) indicates some ability

to scale with problem size.

Clearly the use of selection alone, relying solely

on the initial population for genetic diversity, is a

radical step for a practical algorithm, but we hope

that it points out an important challenge and strength

of all cooperative co-evolution algorithms: the need

to perform subset selection from a large set. Even

with all the components of a good solution present

in the initial population, it is not an easy task to

select those components. Their quality is based

solely on their relationships with each other.

We hope also that we have shown that the

infinite population model, traditionally used in

theoretical models of evolutionary algorithms, can

be used in the algorithms themselves, in practical

implementations. Such a representation of an

evolving population could prove to be extremely

efficient, in terms of computational space and/or

time requirements, for co-evolutionary algorithms.

A final note on future work: there are many more

commercial packages. In addition, there are many

published, academic algorithms for shape nesting,

which have the advantage (over commercial

implementations) of being fully specified in

publications. This comparison study is just the

beginning.

REFERENCES

Dighe, R., Jakiela, M. J., 1996. Solving Pattern Nesting

Problems with Genetic Algorithms: Employing Task

Decomposition and Contact Detection Between

Adjacent Pieces. Evolutionary Computation, 3, 239-

266.

Goldberg, D. E., Richardson, J., 1987. Genetic algorithms

with sharing for multi-modal function optimization. In

Grefenstette, J. (Ed.), Proceedings of the Second

International Conference on Genetic Algorithms pages

(pp. 41-49). Hillsdale, NJ: L. Erlbaum Associates.

Horn, J., 2002. Resource-based fitness sharing. In

Guervós, J. J. M., Adamidis, P., Beyer, H.-G., Martín,

J. L. F.-V., and Schwefel, H.-P. (Ed.s), Parallel

Problem Solving From Nature (PPSN VII, Lecture

Notes in Computer Science, Vol. 2439, pp. 381-390).

Berlin/Heidelberg: Springer.

Horn, J., 2005. Coevolving species for shape nesting. In

Schaeffer, J. D. (Ed.), The 2005 IEEE Congress on

Evolutionary Computation (IEEE CEC 2005, pp.

1800-1807). Piscataway, NJ: IEEE Press.

Horn, J., 2008. Optimal nesting of species for exact cover

of resources: many against many. In Rudolph, G.,

Jansen, T., Lucas, S., Poloni, C. and Beume, N. (Ed.s),

Parallel Problem Solving From Nature X (PPSN X,

Lecture Notes in Computer, Vol. 5199, pp. 438-448).

Berlin/Heidelberg: Springer.

Kendall, G., 2000. Applying Meta-Heuristic Algorithms to

the Nesting Problem Utilising the No Fit Polygon.

Ph.D. thesis, University of Nottingham.

ICEC 2010 - International Conference on Evolutionary Computation

260