AN ALGORITHM FOR DECISION RULES AGGREGATION

Adam Gudys and Marek Sikora

Institute of Computer Science, Silesian University of Technology, Akademicka 16, 44-100 Gliwice, Poland

Keywords: Decision rules, Decision rules aggregation, Knowledge discovery, Convex hull, Classification.

Abstract: Decision trees and decision rules are usually applied for the classification problems in which legibility and

possibility of interpretation of the obtained data model is important as well as good classification abilities.

Beside trees, rules are the most frequently used knowledge representation applied by knowledge discovery

algorithms. Rules generated by traditional algorithms use conjunction of simple conditions, each dividing

input space by a hyperplane parallel to one of the hyperplanes of the coordinate system. There are problems

for which such an approach results in a huge set of rules that poorly models real dependencies in data, is

susceptible for overtfitting and hard to understand by human. Generating decision rules containing more

complicated conditions may improve quality and interpretability of a rule set. In this paper an algorithm

taking a set of traditional rules and aggregating them in order to obtain a smaller set of more complex rules

has been presented. As procedure uses convex hulls, it has been called Convex Hull-Based Iterative

Aggregation Algorithm.

1 INTRODUCTION

Rules-based data models can be applied for the

classification (Furnkranz, 1999), description (Fayad

et al., 1996), or both the aims simultaneously. In the

case of description or both description and

classification, the possibility of interpretation of

created rules-based data descriptions, thus the ability

to understand and to use dependencies represented

by rules, is their significant feature. Due to the

specificity of the language of classification rules,

defining simple rules-based descriptions is

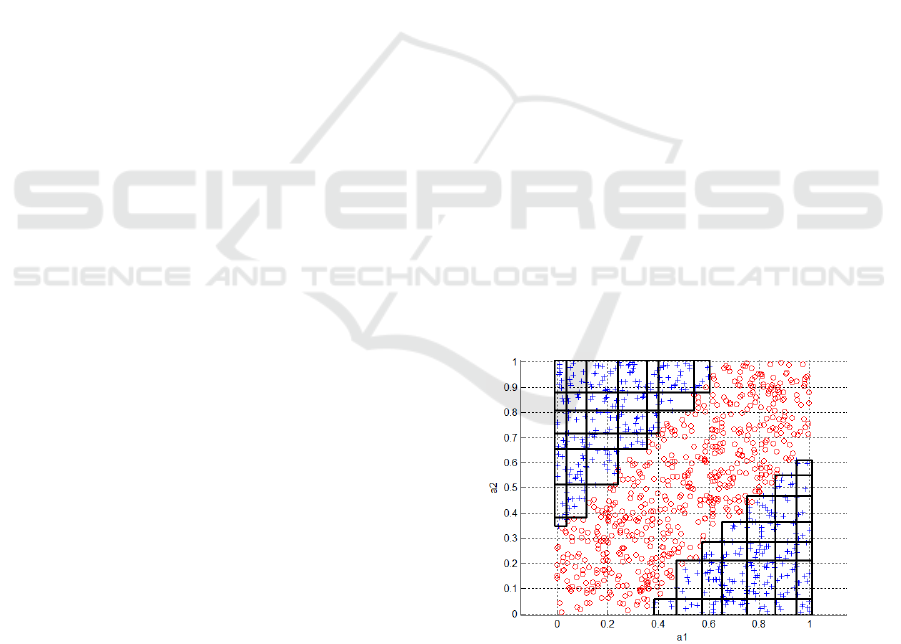
impossible for many problems (Fig. 1). It turned out

that if the language of rules representation is slightly

more complicated, simple and still intuitive

descriptions can be found for many of the problems

(Fig. 2). Therefore a lot of methods search for rules

which premises contain linear combinations of

conditional attributes. This enables to get so-called

oblique descriptors. The majority of the methods

make a decision trees induction (oblique decision

trees) (Murthy et al., 1994), (Bennett, Blue, 1997),

and then transform determined trees into rule sets.

The algorithm ARED (Seunghyun, Ras, 2008)

makes the rules induction with oblique descriptors.

However the efficiency of the algorithm was not

verified on a bigger number of datasets.

Figure 1: Example classification problem. Rules covering

decision regions have been induced using JRip which is an

implementation of the RIPPER algorithm (Cohen, 1995)

contained in Weka software (Hall et al., 2009). One can

see that the simple decision rule language is insufficient to

model the data properly.

Recently, an increasing number of hybrid rules

induction methods has been observed. Joining rules

induction algorithms with support vector machines

(SVM) is the most popular approach (Barakat,

Bradley, 2006), (Martens et al., 2009), (Nunez et al.,

2008). In the papers, SVM are usually used to

concentrate training examples on boundaries of

decision regions or to separate coherent regions in

the features space, and then describe them by rules

216

Gudys A. and Sikora M..

AN ALGORITHM FOR DECISION RULES AGGREGATION.

DOI: 10.5220/0003089702160225

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 216-225

ISBN: 978-989-8425-28-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

with higher dimensional curves (e.g. ellipsoids) in

their premises.

Figure 2: Using a more complicated description language

allows to model classification problem nicely.

Each of the mentioned methods has advantages

as well as disadvantages. The fact that diagonal or

nonlinear descriptors occurring in rules apply all

conditional attributes without offering any pruning

strategies is the disadvantage in the majority of the

methods. The pruning is meant as simplifying multi-

dimensional expressions by eliminating conditional

attributes forming them. Possibility of interpretation

of unpruned rules is then strongly limited.

In the paper, a method of aggregating traditional

classification rules obtained by any standard rule

induction algorithm is presented. The procedure tries

to join rules sequentially, by twos, finding a set of

hyperplanes which bound a region covered by rules

being joined.

The presented method is a generalization of rules

joining algorithms which merge rules without

changing their representation language (Sikora,

2005), (Latkowski, Mikołajczyk, 2004) or operate

on a very specific representation (Pindur et al.,

2004).

In the next part of the paper, an algorithm for

rules aggregation and rules postprocessing, as well

as the results of experiments are presented. The last

chapter includes the summary of obtained results

and directions of further works.

2 BASIC NOTIONS

Some basic notions used later in the paper have been

introduced here.

Let's assume we have a set of objects O which

can be divided into c disjoint classes labelled by

elements of a set 1,2,…,. Information about

assignment of a given object o∈O to a decision class

is included in a value of a decision variable y:

:  



1, 2,… , 



(1)

Let's additionally define a d-element set of attributes

 







,



,…,





. To each object

 we

can assign a d-dimensional vector











,



 containing values of

these attributes. One can see, that it has been

assumed that all the attributes from A are

continuous. This simplification is because the

current version of the algorithm ignores categorical

features in the aggregation process. However, a

generalization for categorical attributes is possible

and has been described later on.

A training set can be defined as follows:

  ,   .

(2)

A classification task consists in finding a function ϕ

which approximates the function y on the basis of a

training set T (which is equivalent to generalising a

knowledge represented by a training dataset).

Rules-based classifiers can be distinguished by

classification strategies they exploit. Described

algorithm is based on a rules hierarchy. This is

because RIPPER algorithm (Cohen, 1995) which

served to generate input rules uses this scheme as

well. The idea is that rules are ordered. During the

classification process the first rule covering an

object being currently checked is picked. Hence,

reordering rules affects classification performance

(which is not the case in different aggregation

strategies like voting rules).

A decision rule can be defined as follows:

:  ,

(3)

where  is a premise consisting of a conjunction of

conditions (descriptors), and  is a conclusion (a

class label). Majority of decision rules induction

algorithms generates simple descriptors like 







or 







. Such conditions divide an input space

into two parts by a hyperplane parallel to one of

hyperplanes of the coordinate system. Aggregation

algorithm covered in this paper generates oblique

descriptors, which are linear combinations of

attributes:

























0.

(4)

Such descriptor divides a feature space by some

hyperplane, not necessarily parallel to coordinate

system hyperplanes. It is assumed, that inequalities

in all descriptors have the same direction (one can

always multiply expression by -1 to obtain this).

AN ALGORITHM FOR DECISION RULES AGGREGATION

217

Several measures that reflect a quality of

decision rules of the form (3) can be computed

(Furnkranz, Flach, 2005), (Guillet, Hamilton, 2007),

(Sikora, 2010). If the rule r is denoted as

→

, then

ϕψ

ϕ¬ψ

=|O

| is the number of objects that

recognize the rule; n

¬ϕ

= n

¬ϕψ

¬ϕ¬ψ

=|O

¬ϕ

| is the

number of objects that do not recognize the rule; n

ϕψ

+ n

¬ϕψ

=|O

| is the number of objects that belong

to the decision class described by the rule; n

¬ψ

ϕ¬ψ

+ n

¬ϕ¬ψ

=|O

¬ψ

| is the number of objects that do

not belong to the decision class described by the

rule; n

ϕψ

=|O

∩O

| is the number of objects that

support the rule. Values n

ϕ¬ψ

, n

¬ϕψ

, n

¬ϕ¬ψ

are

calculated similarly as n

ϕψ

. It can be noticed that for

any rule

→

the inequalities 1

≤

ϕψ

≤|O

0≤n

ϕ¬ψ

≤|O

¬ψ

| hold. Hence, a quality measure is a

function of two variables n

ϕψ

and n

ϕ¬ψ

, and can be

defined as follows (Sikora, 2006):



→

:1,..,|

|

0,..,|

¬ψ

|→.

(5)

Two basic quality measures are accuracy and

coverage:

acc(

→

) = n

(6)

cov(

→

) = n

(7)

The accuracy measure and two other measures are

used for evaluation of joined rules in the aggregation

algorithm. The first measure called RSS is empirical

and enables to evaluate the accuracy and coverage of

a rule simultaneously, taking into consideration

examples distribution among the decision class

indicated by the rule and the other decision classes.

)(

ψϕ

→

Rss

1−

¬¬¬

¬¬

ψϕψϕ

ψϕ

ϕψ

(8)

Making an analysis of the formula (8) it can be

noticed that the measure proposes the method of rule

evaluation analogous to the method of classifiers

sensitivity (first component of the sum) and

specificity (second component of the sum)

evaluation. The measure takes values from the

interval [-1,1] and values equal to zero are achieved

when a rule has the same accuracy as it implies from

the positive and negative examples distribution in a

training set.

The other measure used in a rule evaluation

process is Laplace estimate (9).

)(

ψϕ

→

Laplace

cnn

ψϕϕψ

ϕψ

(9)

The basic idea of the Laplace estimate is to assume

that each rule covers a certain number of examples a

priori. The estimate computes the accuracy, but

starts to count covered positive or negative examples

at a number greater than 0. The positive coverage of

a rule is initialized with 1, while the negative

coverage of a rule is initialized with a number of

decision classes c.

3 CONVEX HULL-BASED

ITERATIVE AGGREAGTION

ALGORITHM

In the following paragraph an algorithm for

aggregation decision rules has been presented. It has

been called Convex Hull-Based Iterative

Aggregation Algorithm. Iterative, because it

sequentially tries to merge decision rules in order to

model the problem more properly than the input rule

set. Convex Hull-Based, because a procedure of

aggregating two particular decision rules uses

convex hulls. On the Fig. 3 one can see a full

flowchart of the algorithm. In the sections below all

steps of the procedure are covered in details.

Example dataset from the Fig. 1 has been used as an

illustration. One must keep in mind that it is

assumed, that input rule set R contains rules

corresponding to a single decision class.

3.1 Hyperrectangular Rules

The idea of the aggregation procedure is based on

the assumption that a decision rule can be

considered as some convex area in a feature space.

The algorithm tries to merge these areas into larger

ones. However, rules generated by traditional

induction algorithms rarely determine convex areas -

to obtain this, a rule should by bounded from both

sides in each dimension forming a hyperrectangle:













,





…











,





.

(10)

This is why the first step of the algorithm consists in

bringing an input rules into a hyperrectangular form.

This can be done by adding missing descriptors with

coordinates of the extreme points from a training set.

It will not affect classification results of unseen data

because these synthetically added descriptors will be

removed after aggregation procedure has finished. In

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

218

addition, hyperrectangular rules have a very nice

feature - one can easily find vertices of the

corresponding hyperrectangles. This is a crucial

issue because in the following steps algorithm uses

these vertices in the merging procedure. The

implication of the proposed approach is that a rule r

can be represented in a dual way:

• as a set of hyperplanes ,

• as a set of vertices .

Keeping integrity between the hyperplane

representation used directly for classification and the

vertex representation which takes part in the

aggregation procedure is a very important task the

algorithm must handle.

3.2 Aggregation Loop

As our aim is to reduce a number of rules in the

entire rule set meeting some classification accuracy

conditions, it must be decided which rules in which

order should be picked for the aggregation

procedure. The simplest approach is to use an

exhaustive paradigm to check all possible rule

permutations and pick the best one. However, the

brute-force method is computationally too expensive

to be used in practice. This is why some greedy

heuristics for searching aggregation candidates has

been proposed.

At the beginning we take the first rule as the

current one and try to merge it with following rules

(let's call those rules aggregation partners) creating a

candidates for new rules. Method of joining two

particular decision rules has been explained in the

following section. For each candidate we check if it

meets quality criterions.

Quality control consists of two elements. At first

algorithm checks how quality of the rule candidate is

related to the better rule from the pair being

aggregated. If it is below some threshold, the

candidate is rejected. Parameter indicating

maximum drop of the quality is called

ruleQualityDrop and is expressed in percentages.

However, checking only this condition may result in

an accumulation of the quality drops and big

classification error of the final rule set. This is why

an additional criterion has been introduced.

Algorithm checks how aggregation of two particular

rules affects classification accuracy obtained by the

entire rule set. If an accuracy decrease exceeds

rulesetAccuracyDrop parameter (which is given in

percentages as well), the candidate is rejected. One

must remember, that these two parameters are

evaluated on a training set. Adjusting them gives full

control on how the algorithm works. For example,

Figure 3: Flowchart of the Convex Hull-Based Iterative

Aggregation Algorithm.

one can force the algorithm to operate in the way

that classification accuracy obtained by a final rule

set does not decrease (on a training set).

If quality criterions are fulfilled, a rule candidate is

accepted. We replace the current rule with the new

one, and remove the partner from the rule set. The

algorithm also checks if the new rule covers some

other rules which follow the partner and removes

them if possible. There is no need to check rules

preceding the partner because they are the ones that

hasn't been aggregated with the current rule (so there

is no possibility that they are covered by the new

rule). After all partners have been checked, we

AN ALGORITHM FOR DECISION RULES AGGREGATION

219

change a current rule for the next one. Procedure

stops when the current rule is the last one from the

rule set.

3.3 Merging Two Decision Rules

This section covers in details how the algorithm

merges two particular decision rules. Let's assume

there are two rules 



and 



we would like to

aggregate. Below steps of the basic aggregation

procedure have been described. The modified

version with some improvements has been

introduced later.

1. Create a new rule r such that 

















.

2. Calculate a d-dimensional convex hull of

points belonging to the 







using Qhull

algorithm (Barber et al., 1996). This

algorithm returns a set 







describing all

the facets of a convex hull. Each facet is

represented by a set of d indices pointing

some vertices from 







3. For each face from 







calculate a

corresponding hyperplane equation.As we

know vertices belonging to each face, this

can be done easily by solving a system of

linear equations. Obtained hyperplanes are

stored in 







set.

Important advantage of the method is that it can be

generalized for categorical attributes easily. Merging

descriptors 



 and 



 simply produces





. Another feature of the procedure is that

it is based only on rule vertices and does not use a

training set.

However, the approach described above has its

disadvantages. Most important one is that a number

of vertices representing a rule grows exponentially

with a number of dimensions. As hyperrectangular

rules use all attributes in their premises, handling

high dimensional feature spaces is computationally

very expensive. This is why, a hull should be

calculated only with respect to dimensions which are

really used in aggregated rules. Therefore, for each

input rule r, before bringing it to a hyperrectangular

form, we store attributes present in a premise in a set

. Additional improvement is to limit maximum

number of dimensions that can appear in a rule being

created. There is an algorithm parameter called

maxDim. If number of attributes in a rule candidate

exceeds this parameter, a rule is not created. This

allows user to control the complexity of obtained

(a)

(b)

Figure 4: Two hyperrectangular rules separately (a) and

after aggregation (b).

descriptors (for example, he can limit number of

dimensions to 3 in order to visualise hyperplanes) or

to speed-up the algorithm. The modified aggregation

procedure of rules 



and 



is as follows:

1. Create a new rule r such that 

















 and 























,







|

. If , reject r

immediately and skip the following steps.

2. Calculate a k-dimensional convex hull of

points from 







with respect to the

attributes belonging to 







. Following

actions are the same as in the previous

description.

The result of aggregation of two example rules has

been presented on the Fig. 4.

3.4 Rule Tuning

One can see on the flowchart that just after creation

of a new rule candidate there is a step called rule

tuning. It comes out that sometimes a rule candidate

may be further improved. This is very important

from the point of view of the algorithm because

quality influences if an aggregated rule is accepted.

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

220

Hence, each candidate is tuned to obtain as good

result as possible.

Rule tuning procedure has two phases. The first

stage of tuning consists in joining coplanar facets

and removing duplicated hyperplanes. As we

mentioned before, in k-dimensional space each facet

of a convex hull calculated by Qhull has k vertices.

This means that, for example, in 3-dimensional

space, we obtain triangular facets. Such approach

may result in coplanar facets. For example cube

contains 6 square facets but Qhull returns 12 triangle

ones. In fact, as our input rules have a

hyperrectangular form, this situation will happen

very often. More the dimensions, more coplanar

facets appear. This is why the algorithm must merge

coplanar facets and remove duplicated hyperplane

equations.

The second stage of tuning consists in adjusting

hyperplanes equations to get the maximum quality

of an aggregated rule. One can see on the Fig. 4 that

the oblique line is not optimally situated (if we

move it slightly upwards it will cover same number

of positive examples and less negative examples).

Hence, we introduce a technique of hyperplane

adjusting. For simplicity it is assumed that only

hyperplane translations are possible (no rotations are

performed). Below we described adjustment steps

for a rule r created as the result of aggregation of

rules 



and 



1. Find a hyperplane to adjust  such

that 



  



 (there is no

need to improve a boundary hyperplane or a

hyperplane that could have already been

improved in one of previous iterations).

2. Find a face f corresponding to the

hyperplane h and all vertices from 

adjacent to the face f. A vertex is adjacent

to the face f if it belongs to some face g

adjacent to f and it does not belong to f .

3. Calculate equations of hyperplanes parallel

to h going through vertices adjacent to f and

choose the one closest to h (let's call it

closest

). Original hyperplane h and the

closest one determine bounds of the

searching area. This is to assure that no face

vanishes in the adjustment procedure.

4. Use Fibonacci search technique (Ferguson,

1960) to find an optimal hyperplane h'

parallel to h lying in the area bounded by h

and h

closest

(as these hyperplanes are

parallel, Fibonacci is used to find an

optimal value of a free term). Assumed

quality measure is used as a criterion

function in searching.

5. Replace h with h' in , calculate new

positions of vertices forming face f using h'

equation and equations of adjacent faces.

This can be easily done by solving a system

of linear equations.

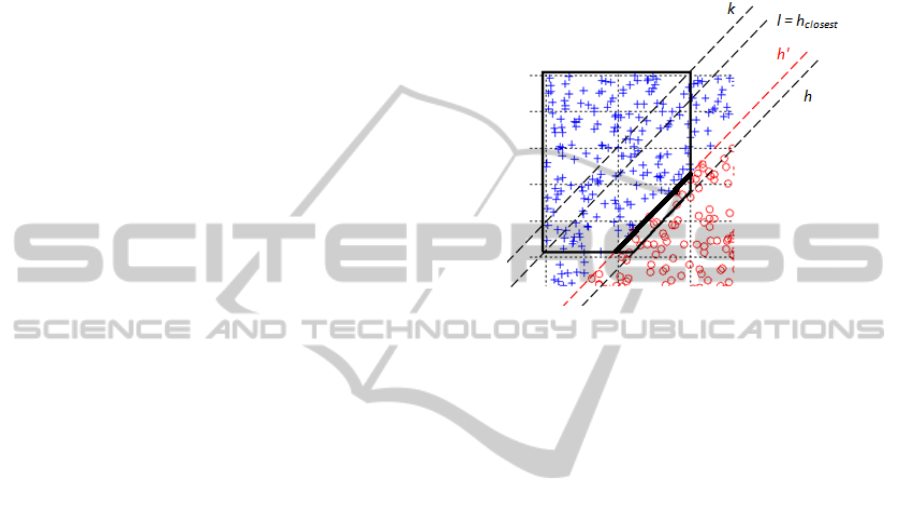
An example of the adjustment procedure has been

shown on the Fig. 5.

Figure 5: Tuning of a rule from the Fig. 4b. Hyperplane h

is the one being adjusted. Hyperplanes h and h

closest

indicate boundaries of the searching area. Hyperplane h' is

an optimal hyperplane found with Fibonacci method.

Adjusted face has been marked with a thick line.

3.5 Rule Set Pruning

Rule set pruning is done at the very end of the whole

procedure after the aggregation loop has finished.

This phase consists of actions that either decrease

rules quality (and should not be done in a tuning

phase preventing from a premature rejection of

candidates) or remove some data from a rule

description so further aggregations become

impossible.

There are two stages of pruning, both are

repeated for all rules in a rule set. First one consists

in eliminating hyperplanes that correspond to the

boundaries of the domain. As it has been said before,

the first step of the Iterative Aggregation Algorithm

is transforming input rules to the hyperrectangular

form. This means that some hyperplanes had to be

synthetically added. After the entire aggregation

procedure has finished, we can remove them.

The second stage of pruning consists in

removing other hyperplanes that have no significant

influence on classification results. Algorithm just

iterates through all the hyperplanes and checks how

deleting affects classifier performance. If a

classification accuracy decrease evaluated on a

training set does not exceed pruningAccuracyDrop

parameter (given in percentages), a hyperplane is

AN ALGORITHM FOR DECISION RULES AGGREGATION

221

removed. Below one can see a comparison between

some rule before and after pruning procedure.

Before pruning:

(-a1+0.602 >= 0) and

(-a1+0.432*a2+0.196 >= 0) and

(-a1+0.63*a2+0.022 >= 0) and

(-0.975*a1+a2-0.277 >= 0) and

(-0.491*a1+a2-0.329 >= 0) and

(-0.991*a2+1 >= 0) and

(+a2-0.348 >= 0) and

(+a1+0.01 >= 0) => class = positive

After pruning:

(-0.975*a1+a2-0.277 >= 0) =>

class = positive

As one can see, the reduction of descriptors number

is significant.

Actions described here cannot be done in the rule

tuning phase. This is because the hyperplane

adjustment procedure uses equations of adjacent

hyperplanes to calculate new positions of face

vertices. If one removed some hyperplanes from









, it would become impossible.

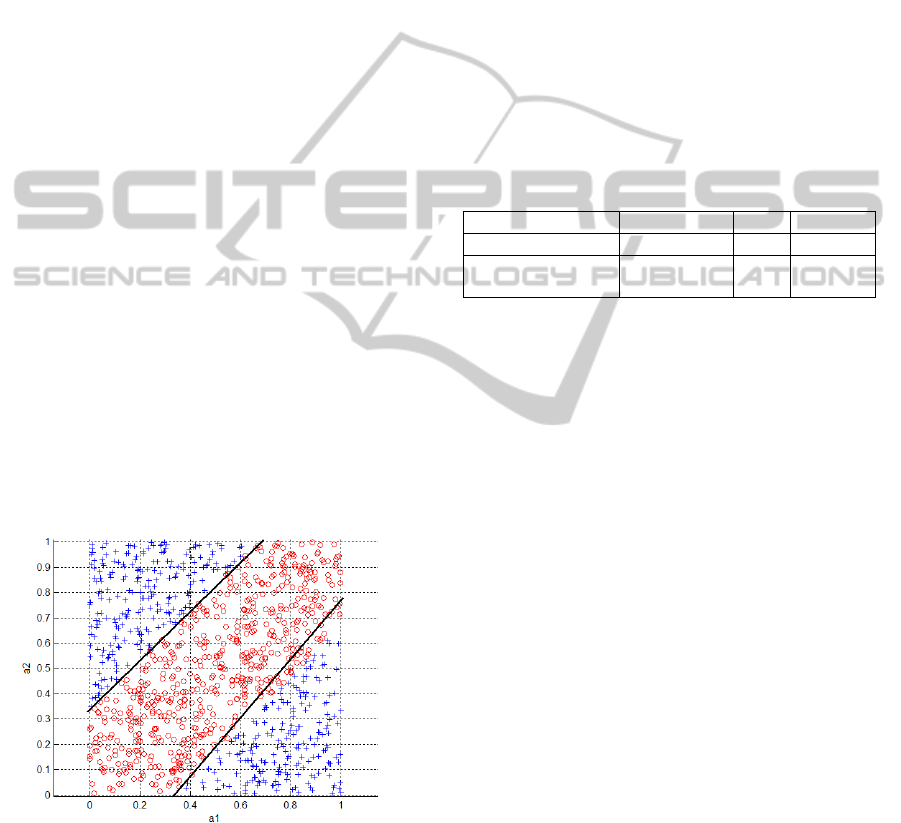
Final results of the algorithm for the example

input rule set has been shown on the Fig 6.

4 EXPERIMENTS

In order to evaluate results of the algorithm some

experiments have been performed. Benchmark

datasets have been chosen mainly from the UCI

Machine Learning Repository. The only exceptions

Figure 6: Final results of the Convex Hull-Based Iterative

Aggregation Algorithm performed on the rule set

presented on the Fig 1.

are synth2D (Fig. 1.) and synth3D datasets, which

have been synthetically generated and sc503 which

is the real dataset containing a microseismic hazard

assessment in a coal mine. Input rules have been

generated using JRip (Hall et al., 2009). Majority of

the experiments have been run in 10-fold cross

validation (only segment dataset has been tested in

the train and test mode). Tests have been performed

with four sets of parameters (from a very

conservative to a very aggressive aggregation

strategies) for the accuracy, RSS and Laplace quality

measures. In each experiment it has been checked

which measure leads to the best accuracy of an

obtained rule set and the best reduction of a number

of rules. Results are presented in the Table 1. One

can see that accuracy is the best quality measure if

we aim in the highest classification accuracy. If one

would like to reduce a number of rules, he should

pick RSS instead.

Table 1: Percentages indicate how often given quality

measure leads to highest accuracy and highest rule

reduction rate.

accuracy RSS Laplace

Highest accuracy 41% 29% 30%

Highest reduction

rate

24% 50% 26%

From all tested parameter sets we have chosen two

which haves been called safe and aggressive

aggregation strategies (see Table 2 for more detailed

description).

Tables 2a and 2b present results of

classification for these parameter sets for accuracy

and RSS quality measures respectively. This is due

to fact that these measures gave the best results from

the point of view of a classifier performance and a

rule set reduction. Results for Laplace have been

omitted, because they are located between accuracy

and RSS. One can see that results for the safe

strategy are similar for both quality measures.

However, in the aggressive strategy RSS leads to

lower accuracy and higher reduction of rule sets.

Below one can see a comparison between input

and output rules for “R” decision class for the

balance-scale data set. Aggressive parameter set has

been used with hyperplane dimensionality limitation

equal to 3. RSS has been set as a rule quality

measure.

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

222

Table 2: Results of classification for the example datasets. Input rule set, and rule sets obtained by the safe and aggressive

aggregation strategies has been evaluated. Corresponding algorithm parameters are 20%-2%-1% and 20%-8%-2%

(ruleQualityDrop-rulsetAccuracyDrop-pruningAccuracyDrop). To speed up the calculations maximum number of

hyperplanes has been limited to 5. Accuracy (table a) and RSS (table b) have been used as quality measures.

(a)

Dataset

Input rule set Safe strategy Aggressive strategy

accuracy

[%]

rules

count

desc.

count

Δ(acc)

[%]

Δ(rc)

[%]

Δ(dc)

[%]

Δ(acc)

[%]

Δ(rc)

[%]

Δ(dc)

[%]

vehicle

67 16,7 42,1 2,3 -7,8 -32,5 0,6 -9 -37,5

wine

90,6 3,7 4,5 1,3 0 -2,22 1,3 0 -8,89

glass

65,4 7,2 14 1,3 -2,8 -7,86 1,5 -4,2 -12,1

iris

92,7 3,7 3,7 0,7 -5,4 -21,6 0,7 -5,4 -21,6

australian

84,1 4,7 8,7 1 -4,3 -14,9 1 -36 -67,8

pima

73,9 3,7 6,3 -0,4 -8,1 -19 -2 -19 -33,3

balance-scale

77,4 11,9 32,6 4,7 -81 -76,1 4,6 -81 -78,2

ionosphere

89,8 4,8 5,2 1 -10 -15,4 -1 -17 -25

heart-statlog

74,4 4 6,1 3 -40 -37,7 3 -43 -42,6

pendigits

86,7 30,8 75,1 -2 -12 -16,6 -4 -14 -18,6

ecoli

83 9,5 16,7 0,7 -6,3 -17,4 0,4 -7,4 -24,6

yeast

57,8 16,7 39,3 1,5 -14 -36,9 -0 -22 -47,8

segment

94,4 13 26 -0,5 -7,7 -15,4 -2 -7,7 -15,4

synth2D

95 10,9 19,8 2,3 -72 -86,4 1,7 -72 -87,9

synth3D

95,8 7,8 19,6 -1 -51 -61,2 -3 -60 -73,5

sc503

90,2 4,1 6,2 0,6 -22 -30,6 -1 -27 -40,3

Average 1,0 -21,5 -30,7 0,1 -26,5 -39,7

(b)

Dataset

Input rule set Safe strategy Aggressive strategy

accuracy

[%]

rules

count

desc.

count

Δ(acc)

[%]

Δ(rc)

[%]

Δ(dc)

[%]

Δ(acc)

[%]

Δ(rc)

[%]

Δ(dc)

[%]

vehicle

67 16,7 42,1 2,6 -16 -37,3 -3 -23 -48,5

wine

90,6 3,7 4,5 1,3 0 -2,22 1,3 0 -8,89

glass

65,4 7,2 14 0,6 -4,2 -9,29 -4 -11 -20

iris

92,7 3,7 3,7 0,7 -5,4 -21,6 0,7 -5,4 -21,6

australian

84,1 4,7 8,7 1 -6,4 -18,4 1 -36 -67,8

pima

73,9 3,7 6,3 -0,9 -11 -23,8 -2 -32 -50,8

balance-scale

77,4 11,9 32,6 6,5 -82 -76,7 5,6 -83 -79,1

ionosphere

89,8 4,8 5,2 0 -4,2 -7,69 -2 -19 -26,9

heart-statlog

74,4 4 6,1 3 -40 -37,7 3 -43 -42,6

pendigits

86,7 30,8 75,1 -2 -15 -16,5 -8 -23 -23,6

ecoli

83 9,5 16,7 0,7 -11 -20,4 -2 -17 -32,3

yeast

57,8 16,7 39,3 1,2 -28 -43,5 -1 -38 -60,1

segment

94,4 13 26 -0,5 -7,7 -15,4 -5 -23 -42,3

synth2D

95 10,9 19,8 2,2 -72 -86,9 2,1 -72 -87,9

synth3D

95,8 7,8 19,6 -1 -51 -57,7 -6 -71 -76,5

sc503

90,2 4,1 6,2 0 -27 -33,9 -1 -27 -38,7

Average 1,0 -23,8 -31,8 -1,3 -32,7 -45,5

AN ALGORITHM FOR DECISION RULES AGGREGATION

223

Input rule set:

(right-weight >= 3) and (right-distance

>= 3) and (left-weight <= 2) =>

class=R

(left-distance <= 2) and (right-weight

>= 3) and (right-distance >= 3) =>

class=R

(left-weight <= 3) and (left-distance

<= 2) and (right-weight >= 2) and

(right-distance >= 2) => class=R

(left-weight <= 1) and (left-distance

<= 3) and (right-distance >= 3) =>

class=R

(left-distance <= 1) and (right-weight

>= 3) and (left-weight <= 4) =>

class=R

(left-weight <= 1) and (right-distance

>= 2) and (right-weight >= 2) =>

class=R

(right-distance >= 4) and (right-weight

>= 4) and (left-weight <= 3) =>

class=R

(right-weight >= 5) and (right-distance

>= 4) and (left-weight <= 4) =>

class=R

(left-distance <= 3) and (right-weight

>= 3) and (right-distance >= 4) =>

class=R

(left-distance <= 3) and (right-weight

>= 4) and (right-distance >= 2)

and (left-weight <= 3) => class=R

(left-distance <= 1) and (right-weight

>= 2) and (right-distance >= 2) =>

class=R

(left-weight <= 3) and (left-distance

<= 1) and (right-distance >= 4) =>

class=R

Output rule set:

(-0.5*left-distance+1 >= 0) and

(+0.5*right-weight-1 >= 0) =>

class=R

(-0.5*left-weight+0.75*right-distance-

1 >= 0) and (+0.5*right-weight-1

>= 0) => class=R

(-0.333*left-distance+0.666*right-

weight-1 >= 0) and (+0.5*right-

distance-1 >= 0) => class=R

(-0.333*left-distance+1 >= 0) and

(+0.5*right-distance-1 >= 0) and

(+0.25*right-weight-1 >= 0) =>

class=R

(-left-distance+1 >= 0) => class=R

(-0.25*left-weight-0.25*left-

distance+1 >= 0) => class=R

One can see that rule reduction rate is significant.

The appearance of oblique descriptors allowed to

decrease the number of rules describing the training

data set and to reflect better dependences occurring

in the “R” decision class. Determined rules are

consistent with the balance scale dataset specificity.

In the case of the 2D synthetic dataset rules such

as in Fig. 6 were managed to obtain. It clearly shows

that the almost perfect description of the dataset has

been obtained. Obtaining the perfect one (as in the

Fig. 2) would be possible in the case of rotation of

one oblique descriptor by a certain angle. Such

tuning procedure will be the subject of further works

with the purpose of improving the algorithm.

5 CONCLUSIONS

The proposition of an algorithm for classification

rules aggregation that enables to introduce oblique

descriptors in rules premises is presented in the

paper. The aim of the algorithm is rules aggregation

in order to obtain less number of rules describing

decision classes. At the same time, the decrease of a

rules number should not influence negatively the

generalization abilities of the rules-based classifier.

Research results presented in tables 2a and 2b

show that the algorithm operates according to the

assumptions. Reduction of a number of rules and

descriptors occurring in their premises is the result

of the algorithm. The decrease of descriptors number

is obviously caused, among others, by the fact that

descriptors of aggregated rules can be linear

combinations of several attributes, so they are more

complicated than input ones. However, as the

example of the synthetic dataset presented in the

previous section shows, the change of descriptors

representation can be helpful in better understanding

dependencies in data.

The procedure tries to join rules sequentially, by

twos, finding a set of hyperplanes which limit a

region covered by rules being joined. Boundary

conditions added synthetically to premises of

aggregated rules are used in the hyperplanes

searching only.

The algorithm can be parameterized by using

various rule quality measures and various threshold

values connected with a quality of joined rules and

their classification abilities. As tables 2a and 2b

show, values of parameters are important for the

efficiency of the algorithm.

Further works on improving the algorithm

performance will concern developing more

advanced tuning strategy of joined rules. Beside the

method of a hyperplane translation, a strategy of its

rotation around a given point by a given angle will

be worked out. Probably, authors will take

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

224

advantage of experiences described by Murthy et al.

(1994).

The algorithm sources (written entirely in

MATLAB) can be provided after sending a request

to one of the authors.

ACKNOWLEDGEMENTS

This work was supported by the European

Community from the European Social Fund.

REFERENCES

Barakat, N., Bradley, A. B., 2006. Rule Extraction from

Support Victor Machines: Measuring the Explanation

Capability Using the Area under the ROC Curve. In

18th International Conference on Pattern Recognition.

Hong Kong, 2006.

Barber, C. B., Dobkin, D. P., Huh, H., 1996. The

Quickhull algorithm for convex hulls. ACM

Transactions on Mathematical Software, pp.469-83.

Bennett, K. P., Blue, J. A., 1997. A support vector

machine approach to decision trees. Department of

Mathematical Sciences Math Report No. 97-100.

Cohen, W. W., 1995. Fast effective rule induction. In

International Conference on Machine Learning.

Tahoe City, 1995. Morgan Kaufmann.

Fayad, U. M., Piatetsky-Shapiro, G., Smyth, P.,

Uthurusamy, R., 1996. From data mining to

knowledge discovery. In Advances in knowledge

discovery and data mining. Cambridge, 1996.

AAAI/MIT-Press.

Ferguson, D. E., 1960. Fibonaccian searching.

Communications of the ACM, December. p.648.

Furnkranz, J., 1999. Separate-and-conquer rule learning.

Artificial Intelligence Review, pp.3-54.

Furnkranz, J., Flach, P. A., 2005. ROC ‘n’ Rule Learning

– Towards a Better Understanding of Covering

Algorithms. Machine Learning, pp.39-77.

Guillet, F., Hamilton, H. J., 2007. Quality measures in

data mining. New York: Springer-Verlag.

Hall, M., Eibe, F., Holmes, G., Pfahringer, B., Reutemann,

P., Witte, I. H., 2009. The WEKA Data Mining

Software: An Update. SIGKDD Explorations.

Latkowski, R., Mikołajczyk, M., 2004. Data

Decomposition and Decision Rule Joining for

Classification of Data with Missing Values.

Transactions on Rough Sets I, pp.299-320.

Martens, D., Baesens, B., Gestel, T. V., 2009.

Decompositional Rule Extraction form Support Vector

Machines by Active Learning. IEEE Transaction on

Knowledge and Data Engineering, pp.178-91.

Murthy, S. K., Kasif, S., Salzberg, S., 1994. A system for

induction oblique decision trees. Journal of Artificial

Intelligence Research, pp.1-31.

Murthy, S. K., Kasif, S., Salzberg, S., 1994. A system for

induction oblique decision trees. Journal of Artificial

Intelligence Research 2, pp.1-31.

Nunez, H., Angulo, C., Catalia, A., 2008. Rule extraction

on support and prototype vectors. In J. Diederich, ed.

Rule extraction form SVM. Springer. pp.109-33.

Pindur, R., Susmaga, R., Stefanowski, J., 2004.

Hyperplane aggregation of dominance decision rules.

Fundamenta Informaticae, pp.117-37.

Seunghyun, I., Ras, Z. W., 2008. Action Rule Extraction

from a Decision Table: ARED. In ISMIS. Toronto,

2008. Lecture Notes in Computer Science.

Sikora, M., 2005. An algorithm for generalization of

decision rules by joining. Foundation on Computing

and Decision Sciences, Vol. 30, No. 3, pp.227-39.

Sikora, M., 2006. Rule Quality Measures in Creation and

Reduction of Data Rule Models. In Lecture Notes in

Artificial Intelligence Vol. 4259. Berlin Heidelberg:

Springer-Verlag. pp.716-25.

Sikora, M., 2010. Decision rules based data models using

TRS and NetTRS – method and algorithms.

Transactions on Rough Sets XI. Lecture Notes on

Computer Sciences Vol.5946, pp.130-60.

AN ALGORITHM FOR DECISION RULES AGGREGATION

225