INTERLEAVING FORWARD BACKWARD FEATURE SELECTION

Michael Siebers and Ute Schmid

Cognitive Systems Group, Otto-Friedrich-University, Feldkirchenstr. 21, 96052 Bamberg, Germany

Keywords:

Feature selection, Forward selection, Backward elimination.

Abstract:

Selecting appropriate features has become a key task when dealing with high-dimensional data. We present a

new algorithm designed to ﬁnd an optimal solution for classiﬁcation tasks. Our approach combines forward

selection, backward elimination and exhaustive search. We demonstrate its capabilities and limits using artiﬁ-

cial and real world data sets. Regarding artiﬁcial data sets interleaving forward backward selection performs

similar as other well known feature selection methods.

1 INTRODUCTION

The selection of relevant features is crucial for

successful concept formation and classiﬁer learning

(Blum and Langley, 1997; Liu and Motoda, 1998).

Especially for data with very high dimensionality,

many standard machine learning algorithms cannot

be applied directly—as ﬁrst step, the number of fea-

tures needs to be reduced to a subset of promising

candidates. Less features imply concept or classiﬁer

learning is faster, produces easier comprehensible and

maybe more effective and efﬁcient results.

In general, the feature selection problem can be

characterized as the task of “choosing a small subset

of features that ideally is necessary and sufﬁcient to

describe the target concept” (Kira and Rendell, 1992,

p.129).

2 REQUIREMENTS

This study is conducted within a project comparing

different classiﬁers on a single task. The number of

features will be around 60,000. Consequently exhaus-

tive feature subset generation is not recommended,

rather a heuristic guided approach is chosen.

As we want to compare different learning algo-

rithms it is necessary that the feature selection al-

gorithm doesn’t advantage one speciﬁc classiﬁcation

method. Choosing features using a classiﬁcation al-

gorithm as performance evaluator biases the selected

features towards that classiﬁer. Therefore we choose

the inconsistency rate as evaluation function. It mod-

els the rate of instances that is necessarily misclassi-

ﬁed if the instances are fully split according to all se-

lected features. It is monotonic regarding the subset

relation, i.e. removing attributes from a feature sub-

set cannot decrease the inconsistency rate.

Liu and

Motoda (1998, p. 76) deﬁned it as follows:

The inconsistency rate is calculated as follows:

(1) two instances are considered inconsistent if they

are the same except for their class labels (we call

these instances as matching instances), ... (2) the

inconsistency count is the number of all the match-

ing instances minus the largest number of instances

of different class labels, ... and (3) the inconsis-

tency rate is the sum of all the inconsistency counts

divided by the total number of instances (N).

The algorithm should run until an optimal

set is

found. But as ﬁnding an optimal feature subset might

be infeasible depending on the data the algorithm was

designed as anytime algorithm (Zilberstein, 1996).

3 ALGORITHMS

In this section we will present our solution for the

task given in the previous section. First we will give

some preliminaries and notation details, then we will

present our algorithm.

3.1 Preliminaries

Let F = {F

, . . . , F

} denote the set of all features. A

set of features F is called valid iff its inconsistency

A prove outline for the monotonicity of the inconsis-

tency rate is given by Liu, Motoda and Dash (1998).

For a deﬁnition of optimality see section 3.1.

454

Siebers M. and Schmid U..

INTERLEAVING FORWARD BACKWARD FEATURE SELECTION.

DOI: 10.5220/0003093204540457

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 454-457

ISBN: 978-989-8425-28-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Properties of the used artiﬁcial data sets.

Data Set Features Instances Class Type Feature Type Noise Known Relevant Features

Monk1 6 124 binary nominal no A1,A2,A5

Monk2 6 169 binary nominal no A1,A2,A3, A4, A5,A6

Monk3 6 122 binary nominal yes,5% A2, A4, A5

Parity5+5 10 100 binary binary no B2, B3,B4,B6, B8

rate doesn’t exceed a certain threshold t.

Assume two valid feature subsets F

and F

. Set

is said to be better than F

iff F

has less features

or has an equal number of features but a lower incon-

sistency rate.

A feature subset F is now called optimal iff there

exists no other set F

′

that is better than F .

3.2 IFBS

The Interleaving Forward Backward Selection algo-

rithm (IFBS) consists of four phases (Alg. 1). In the

ﬁrst phase the algorithm adds features to an initially

empty set until its inconsistency rate falls below a cer-

tain threshold t. This is done in a greedy way.

During the second phase as much features as pos-

sible are removed while the inconsistency rate of the

feature set doesn’texceed the thresholdt. During both

phases the algorithm keeps track of evaluated subsets.

Subsets are evaluated once, subsets of known invalid

subsets are not evaluated.

In the third phase the algorithm starts with the full

feature set. In each round all subsets having one ele-

ment less are tested. The subsets of the ﬁrst one being

invalid are excluded from further consideration. Be-

fore each round the effort to search this round and the

savings if an invalid subset is found in this round are

guessed. The phase ﬁnishes—without excluding any

features—if the search effort so far plus the estimated

effort for this round exceeds the potential savings.

Finally in phase IV the remaining possible fea-

ture subsets are searched. Let the feature set found

in phase II (the best set known so far) have l features.

In the ﬁrst round feature subsets having l elements

are checked. As soon as a subset better than the best

known set is found the algorithm preceeds to the next

round using l = l − 1.

The algorithm continues until

l = 0 or no more valid subset is found.

If the best known set has minimal inconsistency rate,

i.e. 0.0 or the inconsistency rate of the full set, no better set

having the same number of features can be found. Conse-

quently the algorithm preceeds with one (additional) feature

less. This also holds for the ﬁrst round.

4 EVALUATION

For evaluating our approache we implemented it as a

RapidMiner operator. RapidMiner is an open source

data mining and machine learning tool freely avail-

able at http://rapid-i.com.

We compared the performance of our approach

with related work. First we compared it on artiﬁcial

data sets publically available. Afterwards we used

real life data from a feature selection challenge.

4.1 Artiﬁcial Data Sets

As ﬁrst experiments we decided to run our algorithms

on artiﬁcial data sets. For these data sets the rele-

vant features were known a priori. So we were able to

judge the outcome of IFBS objectively.

For each data set IFBS was run using thresholds

of 0.10, 0.05, 0.01 and 0.00. Each combination was

executed 10 times to show effects of random steps in

IFBS and to estimate runtimes better.

We will now ﬁrst describe the artiﬁcial data sets

used, then we will line out the results.

4.1.1 Data Sets

We decided on the Monk’s problems (Thrun et al.,

1991) and Parity5+5 (John et al., 1994) as artiﬁcial

data sets. These data sets have already received atten-

tion in literature and results from different feature se-

lection algorithms are available (Koller and Sahami,

1996; Liu and Motoda, 1998). The data sets are all

available from the UCI Machine Learning Reposi-

tory

or from sgi

4.1.2 Results

In general the results are satisfying. IFBS returned ad-

equate feature sets in apparently no time. The results

for the respective data sets can be seen in Table 3. For

The UCI Machine Learning Repository can be found

online at http://archive.ics.uci.edu/ml/.

Some data sets which were previously available at the

UCI Machine Learning Repository are still available online

at http://www.sgi.com/tech/mlc/db/.

INTERLEAVING FORWARD BACKWARD FEATURE SELECTION

455

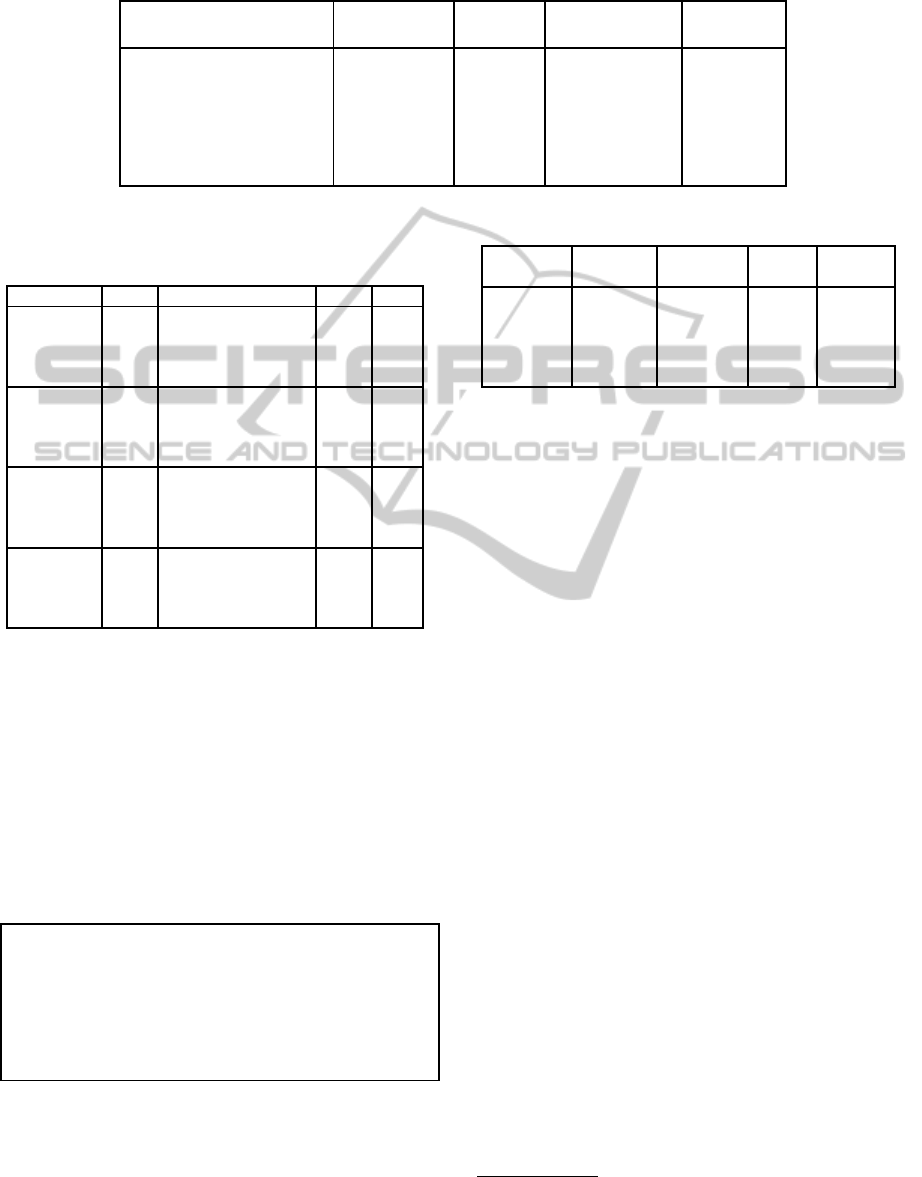
Table 2: Selected features for artiﬁcial data sets. Results not presented in this work are taken from literature (Liu and Motoda,

1998, p.119).

Method Monk1 Monk2 Monk3 Parity5+5

(A1, A2, A5) (A1–A6) (A2,A4, A5) (2–4,6,8)

Branch & Bound A1, A2, A5 A1–A6 A1, A2, A4, A5 2–4,6,8

Quick Branch & Bound A1, A2, A5 A1–A6 A1, A2, A4, A5 2–4,6,8

Focus A1, A2, A5 A1–A6 A1, A2, A4, A5 2–4,6,8

LVF A1, A2, A5 A1–A6 A1, A2, A4, A5 2–4,6,8

IFBS (t = 0.05) A1, A2, A5 A1–A6 A2, A4, A5 2–4,6, 8

IFBS (t = 0.00) A1, A2, A5 A1–A6 A1, A2, A4, A5 2–4,6,8

Table 3: Results for the different artiﬁcial data sets. t de-

notes the threshold, G the selected feature set, i the incon-

sistency rate of G and r the average runtime in ms.

t G i r

Monk1 0.10 A1, A2,A5 0.00 199

0.05 A1,A2, A5 0.00 200

0.01 A1,A2, A5 0.00 203

0.00 A1,A2, A5 0.00 207

Monk2 0.10 A2–A6 0.09 222

0.05 A1–A6 0.00 231

0.01 A1–A6 0.00 227

0.00 A1–A6 0.00 226

Monk3 0.10 A2,A5 0.07 239

0.05 A2,A4, A5 0.05 239

0.01 A1, A2,A4, A5 0.00 245

0.00 A1, A2,A4, A5 0.00 239

Parity5+5 0.10 B2,B3, B4,B6,B8 0.00 342

0.05 B2, B3,B4, B6, B8 0.00 358

0.01 B2, B3,B4, B6, B8 0.00 348

0.00 B2, B3,B4, B6, B8 0.00 372

Monk1 and Parity5+5 the ideal feature subset com-

bination is found regardless of the threshold chosen.

For Monk2 and a threshold of 0.10 the known rele-

vant feature A1 is not part of the result. For Monk3

and a threshold lower than the innate noise (5% of the

instances are misclassiﬁed) results in selection of the

known not relevant feature A1. The algorithm seems

to be prone to overﬁtting.

In Table 2 the results of IFBS are contrasted with

results from other feature selection methods. Our new

approache is not worse than the other approaches.

Input: features F , threshold t

G ← SelectFeatures(F , t) (PhaseI)

G ← EliminateFeatures(G , t) (PhaseII)

inv ← InvalidSubset(F , t) (PhaseIII)

G ← SearchFinalLevels(F , G , inv, t) (PhaseIV)

return G

Algorithm 1: IFBS.

Table 4: Properties of real world data sets.

Data Set Features Instances Class Feature

Type Type

Arcene 10,000 100 binary integer

Gisette 5,000 6,000 binary integer

Dexter 20,000 300 binary integer

Dorothea 100,000 800 binary binary

Madelon 500 2,000 binary integer

4.2 Real World Data Sets

After evaluating IFBS and IFBSc on artiﬁcial data

sets we used real life data, too. For having compa-

rable results at hand we decided to use the data sets

from 2003’s feature selection challenge organized by

the Feature Extraction Workshop at the Neural Infor-

mation Processing Systems Conference (NIPS)

Evaluation on the real world data sets is a two

step process. First we conducted the feature selection

and reduced the data sets accordingly,then we learned

classiﬁers using a decision tree approach and applied

those to the unlabeled challenge data sets. The ﬁnal

results were submitted to the challenge’s homepage

using the name IFBS-DT. After describing the data

sets we will give both types of results: the selected

features and achieved classiﬁcation quality.

4.2.1 Data Sets

The ﬁve data sets provided for this challenge are ob-

fuscated versions of real world data sets with added

random attributes. All data sets were split into train-

ing, test, and validation set by the callenge organizers.

Test and validation sets were unlabeled. All data sets

are available at the challenge’s homepage. Table 4

summarizes the used data sets.

To run IFBS on the data sets having integer-valued

features these features were discretized based on en-

tropy (Fayyad and Irani, 1993). For all data sets fea-

tures having only one value were excluded.

http://www.nipsfsc.ecs.soton.ac.uk

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

456

Table 5: Selected features for NIPS data sets. Used is the number of features after discretizing and eliminating single-values

features, Probes the number of false positives among selected features

Data Set Features Probes BER

Initial Used Selected # % Training Validation Test

Arcene 10,000 758 6 2 33.33 0.000 0.387 0.369

Gisette 5,000 1,396 23 0 0.00 0.035 0.073 0.064

Dexter 20,000 45 20 0 0.00 0.073 0.143 0.145

Dorothea 100,000 88,120 11 3 27.27 0.078 0.238 0.187

Madelon 500 13 13 0 0.00 0.081 0.210 0.192

4.2.2 Results

Selected Features. Selection of Madelon features

run in a few seconds. The other selection experi-

ments were stopped after several days. Selection for

Dorothea stopped in phase II others in phase III or IV.

Table 5 shows the decrease of feature count during

the selection process. For all data sets the percentage

of features selected was less than 3%. For Gisette,

Dexter and Madelon no irrelevant features were se-

lected. For Arcene and Dorothea high percentages of

false positives were scored. Nevertheless the absolute

number is small (2 and 3, respectively). This is even

more promising as most runs hadn’t ﬁnished.

Classiﬁcation Accuracy. The classiﬁcation accu-

racy is measured as balanced error rate (BER) which

is the average of the errors for each class. BERs for

the data sets are shown in Table 5. For Arcene there

seems to be some overﬁtting as a full discriminating

feature set (no inconsistency) isn’t sufﬁcient for pre-

dicting unseen instances. For all data sets IFBS plus

a decision tree learner was ranked in the third quar-

tile of the challenge’s submissions. A more elaborate

classiﬁcation schema might produce better results.

5 CONCLUSIONS

IFBS has substantial skills to select features for a clas-

siﬁcation task. Results are not worse, but also not

better than other feature selection methods. Further

evaluation is needed. Also new ﬁndings in current re-

search should be taken into account.

The results for the NIPS classiﬁcation task showed

that IFBS can be applied in a practical setting. The

quality of the classiﬁcation could clearly be improved

using a more sophisticated learning procedure.

It could not be shown that IFBS is applicable

for high-dimensional data sets. Further work should

tackle this issue ﬁrst.

REFERENCES

Blum, A. L. and Langley, P. (1997). Selection of relevant

features and examples in machine learning. Artiﬁcial

Intelligence, 97(2):245–271.

Fayyad, U. M. and Irani, K. B. (1993). Multi-Interval Dis-

cretization of Continuous-Valued Attributes for Clas-

siﬁcation Learning. In Bajcsy, R., editor, IJCAI 1993,

pages 1022–1029, San Mateo, Calif. Morgan Kauf-

mann.

John, G. H., Kohavi, R., and Pﬂeger, K. (1994). Irrelevant

Features and the Subset Selection Problem. In Cohen,

W. W. and Hirsh, H., editors, ICML 1994, pages 121–

129. Morgan Kaufmann.

Kira, K. and Rendell, L. A. (1992). The Feature Selection

Problem: Traditional Methods and a New Algorithm.

In Swartout, W. R., editor, AAAI Conference on Arti-

ﬁcial Intelligence 1992, pages 129–134, Menlo Park.

AAAI Press [u.a.].

Koller, D. and Sahami, M. (1996). Toward Optimal Fea-

ture Selection. In Saitta, L., editor, ICML 1996, pages

284–292, San Francisco, Calif. Morgan Kaufmann;

Kaufmann.

Liu, H. and Motoda, H. (1998). Feature selection for

knowledge discovery and data mining, volume 454 of

Kluwer international series in engineering and com-

puter science. Kluwer Academic Publ., Boston.

Liu, H., Motoda, H., and Dash, M. (1998). A Monotonic

Measure for Optimal Feature Selection. In Nedellec,

C. and Rouveirol, C., editors, ECML 98, volume 1398

of Lecture Notes in Computer Science, pages 101–

106. Springer.

Thrun et al., S. (1991). The Monk’s problems: A perfor-

mance comparison of different learning algorithms.

Zilberstein, S. (1996). Using Anytime Algorithms in Intel-

ligent Systems. AI Magazine, 17(3):73–83.

INTERLEAVING FORWARD BACKWARD FEATURE SELECTION

457