KERNEL OVERLAPPING K-MEANS FOR CLUSTERING IN
FEATURE SPACE
Chiheb-Eddine Ben N’Cir, Nadia Essoussi
LARODEC, University of Tunis, Tunis, Tunisia
Patrice Bertrand
Ceremade, Universit
´
e Paris-Dauphine, Paris, France
Keywords:
Overlapping clustering, Overlapping K-Means, Kernel Methods, Gram matrix, Kernel induced distance mea-
sure.
Abstract:
Producing overlapping schemes is a major issue in clustering. Recent overlapping methods rely on the search
of optimal clusters and are based on different metrics, such as Euclidean distance and I-Divergence, used to
measure closeness between observations. In this paper, we propose the use of kernel methods to look for
separation between clusters in a high feature space. For detecting non linearly separable clusters, we propose
a Kernel Overlapping K-Means algorithm (KOKM) that is based on a kernel induced distance measure. The
number of overlapping clusters is estimated using the Gram matrix. Experiments on different datasets show the
correctness of the estimation of number of clusters and show that KOKM gives better results when compared
to overlapping k-means.
1 INTRODUCTION
Overlapping between clusters is a major issue in clus-
tering. In this cluster configuration, an object can be-
long to one or many clusters without any membership
coefficient. Based on the assumption that an object
really belongs to many clusters, overlapping cluster-
ing is different from both crisp and fuzzy clustering.
A number of real problems require to find overlap-
ping clusters in order to fit the data set structure. For
example, in social network analysis, community ex-
traction algorithms should be able to detect overlap-
ping clusters because an actor can belong to multiple
communities (Banerjee et al, 2005); in video classifi-
cation, overlapping clustering is a necessary require-
ment while video can potentially have multiple gen-
res.
Several overlapping clustering models based on
stratified and partitioning approaches were proposed
in the literature. Examples of stratified models are
pyramids (Diday, 1984), which are structures less
restrictive than the trees, and k-weak hierarchies
(Bertrand and Janowitz, 2003), which are a general-
ization of the pyramids. Since these models include
specific constraints on clusters, they suffer from the
major drawback that the number of feasible object as-
signments is reduced.
Overlapping methods based on some partitioning
approach extend primarily methods of strict or fuzzy
classification to produce overlapping clusters. Sev-
eral clustering methods have been used such as soft k-
means and Threshold Meta-clustering Algorithm (De-
odhar and Ghosh, 2006). The main issue in these
methods is the prior threshold which is difficult to
learn. In addition, the criteria optimized successively
by these partitioning methods look for an optimal par-
tition without introducing the overlap between data in
an optimization step (Cleuziou, 2009).
More recent models for overlapping clustering
solve these problems and look for optimal clusters.
Banerjee et al. proposed the Model based Overlap-
ping Clustering (MOC) which is considered as the
first algorithm looking for optimal clusters (Banerjee
et al, 2005). This algorithm is inspired from biology
and is based on the Probabilistic Relational Model
(PRM). Cleuziou proposed the Overlapping K-Means
algorithm (OKM) which is considered as a general-
ization of k-means to detect overlap between clusters
(Cleuziou, 2007). These methods cannot detect non-
linearly separable clusters, thus fail to produce clus-
250
Ben N’Cir C., Essoussi N. and Bertrand P..
KERNEL OVERLAPPING K-MEANS FOR CLUSTERING IN FEATURE SPACE.
DOI: 10.5220/0003095102500256
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 250-256
ISBN: 978-989-8425-28-7
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

ters with complex boundaries. Moreover, it assumes
that the number of clusters is known.
We propose, in this paper, a kernel overlapping
clustering algorithm called Kernel Overlapping k-
Means (KOKM) to produce cluster in a high, possi-
bly infinite, feature space. A non linear mapping of
original data to a higher feature space is implicitly re-
alized using Mercer kernels. The clusters prototypes
and objects images are computed in input space and
only distance between objects are computed in feature
space. The proposed KOKM algorithm combines ad-
vantages of kernel k-means algorithm which allows
detection of non linearly separable clusters and ad-
vantages of OKM algorithm which produces overlap-
ping clusters. In addition, to deal with the number of
overlapping clusters that is prior fixed in OKM, we
estimate this number using the Gram matrix.
This paper is organized as follows: Section 2
describes kernel k-means algorithm and OKM algo-
rithm. Section 3 presents the approximate method
used to estimate the number of overlapping clusters
and describes the proposed KOKM algorithm. After
that, Section 4 describes experiments and show results
on Iris, EachMovie, and Ionosphere datasets. Finally,
Section 5 presents conclusion and future works.
2 BACKROUND
2.1 OKM: Overlapping K-Means
The algorithm OKM is an extension of the algorithm
k-means to produce overlapping clusters (Cleuziou,
2008). The minimization of the objective function
is performed by itering two steps: 1) computation of
clusters prototypes and 2) multiassignment of objects
to one or several clusters. Given a set of data vectors
X = {x
i
}
N
i=1
with x
i
∈ R
d
, the aim of OKM is to find
a set π = {π
c
}
k
c=1
of k overlapping clusters such that
the following objective function is minimized:
J(π) =
∑
x
i
∈X
kx
i
− im(x
i
)k
2
. (1)
This objective function minimizes the sum of squared
Euclidean distances between object x
i
and its image
im(x
i
) for all x
i
∈ X. Image im(x
i
) is defined as the
gravity center of clusters prototypes to which object
x
i
belongs as shown by eq. (2).
im(x
i
) =
∑
c∈A
i
m
c
/|A
i
|, (2)
where A
i
is the set of clusters to which x
i
belongs and
m
c
is the prototype of cluster c.Algorithm OKM uses
a function PROT OTY PE to update the cluster proto-
types after each assignment stage. This function takes
into account objects that are assigned to several clus-
ters. It guarantees the minimization of the objective
function J and then the convergence of the algorithm
using the following general criterion:
m
h
=
1
∑
x
i
∈π
h
α
i
∑
x
i
∈π
h
α
i
.m
h
i
, (3)
where m
h
i
and α
i
are defined respectively by:
m
i
h
= |A
i
|x
i
−
∑
m
c
∈A
i
\{m
h
}
m
c
, (4)
α
i
= 1/|A
i
|. (5)
For the multiple assignment step, the OKM algorithm
uses the function ASSIGN which enables that objects
are assigned to one or more clusters. This function is
based on a heuristic to minimize the space of possible
assignments. The heuristic consisted in sorting clus-
ters from closest to the farthest then assigning the ob-
jects in the order defined while assignment minimizes
the distance between the object and its image.
The stopping rule of OKM algorithm is character-
ized by two criteria as in k-means. The criteria are:
the maximum number of iterations and the minimum
improvement of the objective function between two
iterations.
This algorithm is not appropriate for clusters that
are non linearly separable. Like k-means, this method
fails when clusters have a complex boundary or when
they are concentric. To deal with this problem in k-
means, many solutions are proposed based on kernel
methods like the method kernel k-means. These solu-
tions map data to a higher feature space and look for
separation in this space.
2.2 Kernel k-means
Kernel k-means (Scholkopf et al, 1998) is an exten-
sion of the standard algorithm k-means to solve the
problem of non-linearly separable clusters. By an
implicit mapping of the data from an input space to
a higher, possibly infinite, feature space, kernel k-
means looks for separation in feature space and solves
the problem of clustering non spherical data that k-
means suffers from. For a finite data sample X, the
kernel function yields a symmetric N × N positive
definite matrix K, where each K
i j
entry is the dot
product between the representations in feature space
φ(x
i
) and φ(x
j
) of objects x
i
and x
j
as measured
by the kernel function (Camastra and Verri, 2005):
K
i j
= K(x
i
,x
j
) = hφ(x
i
),φ(x
j
)i.
KERNEL OVERLAPPING K-MEANS FOR CLUSTERING IN FEATURE SPACE
251

Kernel k-means aims at minimizing the sum of
squared Euclidean errors in feature space as shown
by eq. (6):
J(π) =
N
∑
i=1
k
∑
c=1
P
ic
kφ(x
i
) − m
c
k
2
, (6)
where P
ic
is a binary variable indicating membership
of object x
i
to cluster c. In feature space, the prototype
can’t be computed because the mapping function φ
is generally unknown. However, the clustering error
k φ(x
i
) − m
c
k can be computed using kernel function.
This error measure is defined as follows:
kφ(x
i
) − m
c
k
2
= kφ(x
i
) −
1
N
c
N
c
∑
l=1
φ(x
l
)k
2
,
which can be expressed as:
= K
ii
−
2
N
c
N
c
∑
l=1
K
il
+
1
N
2
c
N
c
∑
p=1
N
c
∑
l =1
K
pl
, (7)
where N
c
is the number of objects that belong to clus-
ter c. To minimize this clustering error function, ker-
nel k-means performs two principal steps: the deter-
mination of the nearest cluster from each object in
feature space and the update of membership matrix of
each object. The stopping rule is defined by the max-
imal number of iterations and the minimal improve-
ment of the objective function between two iterations.
3 KERNEL OVERLAPPING
K-MEANS
Our motivation in this paper is to improve overlapping
clustering quality using advantages of kernel meth-
ods. Firstly, we use the Gram matrix to estimate the
number of clusters. Secondly, we use Mercer kernel
as an implicit non linear mapping of data to a higher
feature space where we look for separation between
overlapping clusters.
3.1 Estimating the Number of Clusters
For overlapping schemes, the overlap between clus-
ters is an important characteristic that affects the de-
termination of the appropriate number of clusters.
However, it’s difficult in real application to make
a good choice between schemes with some clusters
with strong overlap and schemes with many clusters
with small overlap. But, if the overlap is important be-
tween two clusters, it’s more suitable to create a third
cluster to minimize overlapping objects. Following
this approach, the overlap between data is minimized
and the number of clusters is approximately equal to
the number of groups in data.
Based on this assumption that the number of over-
lapping clusters is roughly equal to the number of
clusters, and by taking advantage of the kernel trick,
we can estimate an approximate number of clusters
using the Gram matrix. The kernel matrix (Gram ma-
trix) is the square matrix K ∈ R
N×N
such that K
i j
is
equal to hφ(x
i
),φ(x
j
)i for all x
1
,...,x
N
∈ X.
The Gram matrix can be used to determine the
number of clusters in data. As each element of the
kernel matrix is a dot-product value in the feature
space, the matrix will have a block diagonal struc-
ture when there are well-separated clusters within the
data sets. This diagonal structure block can be used
to determine the number of clusters (Girolami, 2002).
This method was first used in the c-means clustering
(fuzzy clustering), and it’s still interesting for over-
lapping clustering. Thus, through counting the num-
ber of significant eigenvalues of the kernel matrix, we
can obtain the number of clusters (Zhang and Chen,
2002).
3.2 KOKM Algorithm
Mercer kernel functions map data from input space
to high, possibly infinite, dimensional feature space
without computing the non linear mapping function
φ. In Feature space, the distance measure between
any two patterns is given by:
d(φ(x
i
),φ(x
j
)) = kφ(x
i
) − φ(x
j
)k
2
= (φ(x
i
) − φ(x
j
))
T
(φ(x
i
) − φ(x
j
))
= hφ(x
i
),φ(x
i
)i + hφ(x
j
),φ(x
j
)i
−2hφ(x
i
),φ(x
j
)i
= K
ii
+ K
j j
− 2K
i j
. (8)
Since φ is non-linear, d(φ(x
i
),φ(x
j
)) is a class of ker-
nel induced non-Euclidean distance measures (Ben-
Hur et al, 2000). If the kernel used is an RBF kernel,
eq. (8) is reduced to:
kφ(x
i
) − φ(x
j
)k
2
= 2 − 2 exp{
−kx
i
− x
j
k
2
σ
2
}. (9)
In the context of proposing a kernel version for over-
lapping k-means to deal with non spherical clusters,
we propose the KOKM algorithm based on kernel in-
duced distance measure as shown by eq. (8). In this
algorithm we map initial data to a higher feature space
where the objective function J is optimized in this
space. The objective function in KOKM is adapted
to minimize the distance between each object and its
corresponding image in feature space as shown by eq.
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
252

(10). We adopt a new kernel induced distance mea-
sure to replace the original Euclidean norm metric
in OKM. The images of objects are computed in the
original data space so that the clustering results can
be interpreted in the original space.
J(π) =
∑
x
i
∈X
kφ(x
i
) − φ(im(x
i
))k
2
=
∑
x
i
∈X
K
ii
+
∑
x
i
∈X
K
im(x
i
)im(x
i
)
−2
∑
x
i
∈X
K
im(x
i
)i
(10)
In addition to the objective function, we modified
also the function ”ASSIGN” used in OKM to affect
objects to their nearest clusters. The choice of the
nearest center of cluster from any object is performed
in feature space using eq. (11).
m
?
i
= argmin
m
c
kφ(x
i
) − φ(m
c
)k
2
, (11)
in other words, m
?
i
is the nearest cluster proto-
type from object x
i
. We propose a new function
called ”K ASSIGN” where objects are affected to one
or several clusters in feature space. The function
”K ASSIGN” can be described as follows:
Algorithm 1: K
−
ASSIGN(x
i
,{m
1
,...m
k
},A
old
i
) → A
i
.
INPUT x
i
: Vector in R
d
.
{m
1
,...m
k
}: Set of center of k clusters.
A
old
i
: Old affectation of object i.
OUTPUT A
i
: New affectation of x
i
.
1: Compute A
i
using eq. (11) and compute im(x
i
)
with affectations A
i
.
2: Looking for the nearest cluster which is not in-
cluded in A
i
using eq. (11) and compute im’(x
i
)
with affectations A
i
∪ {m
?
}
3: if kφ(x
i
) − φ(im
0
(x
i
))k
2
< kφ(x
i
) − φ(im(x
i
))k
2
then
4: A
i
← A
i
∪ {m
?
}, im(x
i
) = im’(x
i
) and we go to
step 2.
5: else
6: compute im
old
with affectation A
old
i
.
7: if kφ(x
i
) − φ(im(x
i
))k
2
≤ kφ(x
i
) −
φ(im
old
(x
i
))k
2
then
8: return A
i
.
9: else
10: return A
old
i
.
11: end if
12: end if
The prototypes are computed in input space like in
OKM algorithm using the function ”PROT OTY PE”
(Cleuziou, 2008). The distances between objects, and
the distances between objects and prototypes are com-
puted only in feature space. Based on the above func-
tions, to implement kernel overlapping k-means, we
derive the following KOKM algorithm:
Algorithm 2: KOKM(X,t
max
,ε,k) → {π
c
}
k
c=1
.
INPUT X: set of vector in R
d
.
t
max
: maximum number of iterations.
ε: minimal improvement in objective function.
k: number of clusters.
OUTPUT π: set of k clusters.
1: Choose the kernel function and its corresponding
parameters.
2: Initialize centers of clusters with random clusters
prototypes, initialize clusters memberships using
”K
−
ASSIGN” and derive value of the objective
function J
t=0
(π) in iteration 0 using eq. (10).
3: Compute clusters prototypes using function
”PROT OTY PE”.
4: Assign objects to one or several clusters using
”K
−
ASSIGN”.
5: Compute objective function J
t
(π) using eq. (10).
6: if (t < t
max
and J
t
(π) − J
t−1
(π) > ε) then
7: go to step 4.
8: else
9: return the distribution of clusters memberships.
10: end if
4 EXPERIMENTS
Experiments are performed on datasets including ei-
ther overlapping or non overlapping clusters. We used
a computer with 4-GB RAM and 2.1-GHz Intel Core
2 Duo processor and the code was implemented in C.
The construction of Gram matrices and extraction of
eigenvalues was realized in Matlab.
In all the experiments, the best parameter of kernel
function is empirically determined. Since the appro-
priate kernel parameter selection is out of the scope of
this work, we only give the best kernel parameter.
Numerical results obtained by OKM using Eu-
clidean distance are compared to those obtained by
KOKM using Polynomial kernel and RBF kernel. Re-
sults are compared according to three validation mea-
sures: precision, recall and F-measure. These vali-
dation measures attempt to estimate whether the pre-
diction of categories was correct with respect to the
underlying true categories in the data.
Precision is calculated as the fraction of objects
correctly labeled as belonging to the positive class di-
vided by the total number of objects labeled as be-
longing to the positive class. Recall is the fraction of
KERNEL OVERLAPPING K-MEANS FOR CLUSTERING IN FEATURE SPACE
253

objects correctly labeled as belonging to the positive
class divided by the total number of elements that ac-
tually belong to the positive class. The F-measure is
the harmonic mean of precision and recall.
Precision = NCLO/T NLO
Recall = NCLO/T NAC
F-measure =
2 × Precision × Recall/Precision + Recall
where NCLO, T NLO and T NAC are respectively the
number of correctly labled objects, the total number
of labled objects and the total number of objects that
actually belong to the positive class.
4.1 Non Overlapping Datasets
Experiments are performed on two artificial non over-
lapping datasets which are Iris
1
dataset and Iono-
sphere
2
dataset. Iris dataset is traditionally used as
a base’s test for evaluation. It is composed of 150
data in R
4
tagged according to three non-overlapping
clusters (50 objects per class). One of these clusters
”setosa” is known to be clearly separated from the two
others.
Figure 1 shows the most significant eigenvalues of
the Gram matrix. The kernel used is an RBF kernel
with σ
2
= 150. There are at least two clusters, another
clusters looks less important. If we choose to add this
cluster then we obtain less overlap between data. So,
known that Iris doesn’t contain overlaps between data,
it’s more suitable to add this third cluster. The optimal
choice is then three clusters.
Figure 1: Most significant Eigenvalues on Iris dataset.
Then using OKM with Euclidean distance,
KOKM with both RBF and Polynomial kernel and
estimating the number of clusters as k = 3, we run
each algorithm twenty times (with similar initializa-
tions). The mean of results obtained are reported in
Table 1. We note that KOKM with both Polynomial
and RBF kernel gives better classification results than
OKM. The improvement is achieved both in terms of
precision and in terms of recall.
1
cf. http://archive.ics.uci.edu/ml/datasets/Iris.
2
cf. http://archive.ics.uci.edu/ml/datasets/ Ionosphere.
The second artificial dataset is Ionosphere which
is built by a radar system in Goose Bay Labrador. This
radar system has 16 antennas with a total transmitted
power of 6.4 kilowatts. This system analyzes the elec-
trons in the ionosphere. Some electrons show a cer-
tain type of structure in ionosphere. These electrons
determine the first class in the dataset that is the class
”good”. Other electrons show no structure in iono-
sphere. They define the second class in the dataset
that is the class ”bad”.
Table 1: Comparison between OKM and KOKM on Iris
dataset.
Method Precesion Recall F-measure
OKM based
Euclidean distance 0.707 0.900 0.815
KOKM with
RBF kernel 0.771 0.906 0.834
KOKM with
Polynomial kernel 0.808 0.993 0.892
Table 2: Comparison between OKM and KOKM on Iono-
sphere dataset.
Method Precesion Recall F-measure
OKM based
Euclidean distance 0.532 0.689 0.597
KOKM with
RBF kernel 0.560 0.737 0.636
KOKM with
Polynomial kernel 0.580 0.721 0.644
Electrons are transmitted via a signal from the an-
tennas. This signal is described by 34 attributes that
will constitute the size of the database Ionosphere.
The total number of signal in the database is 351 sig-
nals. The characteristic of this dataset is that the two
classes have a concentric shape that will be difficult to
separate by some linear clustering algorithm as shown
in Figure 2.
When we map this data to higher dimensional
space using RBF kernel, it will be easier to find sep-
aration between good and bad electrons. The two
classes lose their concentric shape and become lin-
early separable. Figure 3 shows the most significant
eigenvalues on Ionosphere dataset. There are two im-
portant eigenvalues that we consider as the number
of clusters. Then, we run OKM and KOKM twenty
times (with similar initializations) with k = 2. The
mean of results obtained are presented in Table 2.
Similarly to experiments on Iris data set, this table
shows the usefulness of KOKM with both Polyno-
mial and RBF kernel where improvement is achieved
in terms of both precision and recall.
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
254

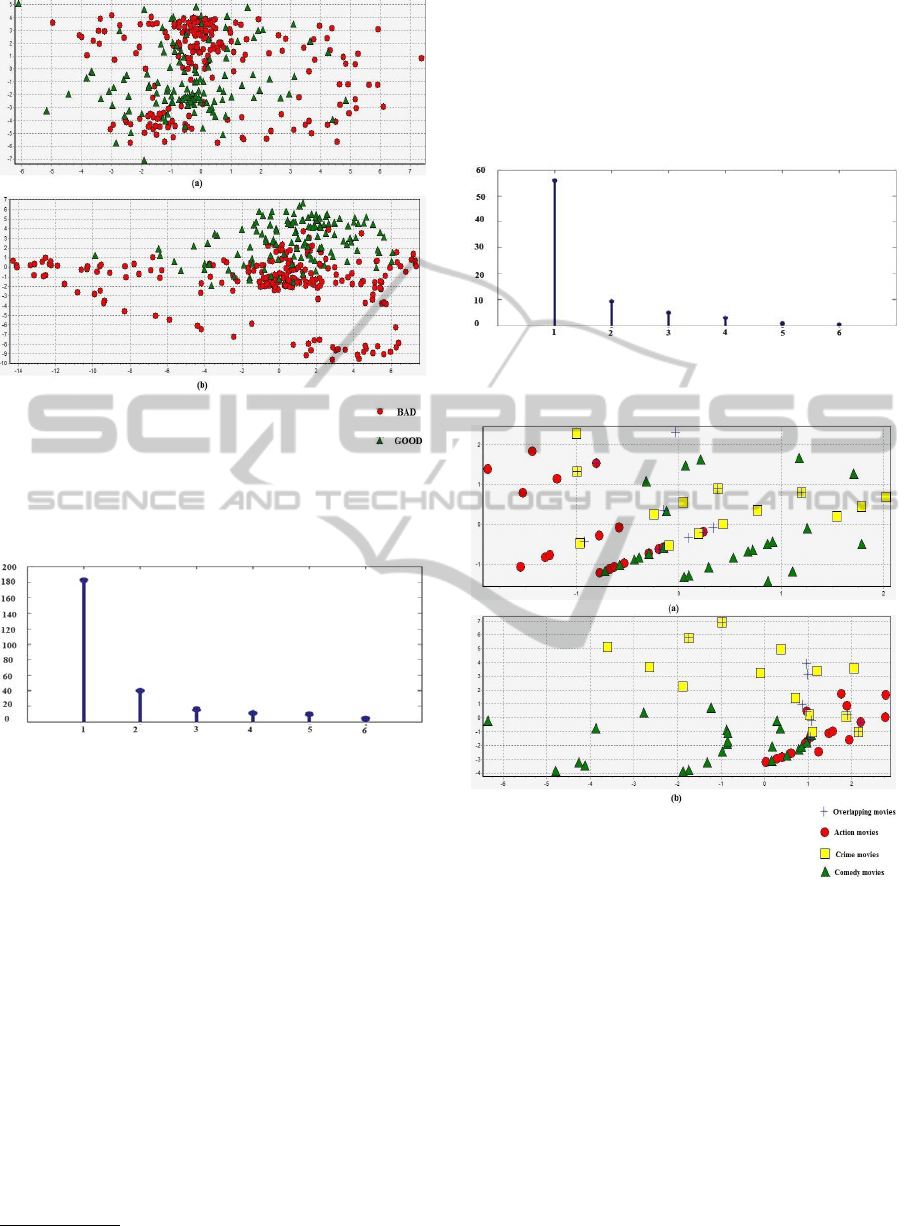
Figure 2: 2D plot of Ionosphere dataset using the first and
second principal axis obtained with PCA: (a) data in input
space (b) data in feature space.
Figure 3: Most significant Eigenvalues on Ionosphere
dataset.
We note that Polynomial kernel give better re-
sults than RBF kernel on both IRIS and Ionosphere
datasets.
4.2 Overlapping Datasets
The EachMovie
3
dataset contains user ratings for
each movie in the collection. Users give ratings on
a scale of 1-5, with 1 indicating extreme dislike and
5 indicating strong approval. There are 74, 424 users
in this dataset, but the mean and the median number
of users voting on any movie are 1732 and 379 re-
spectively. As a result, if each movie in this dataset
is represented as a vector of ratings over all the users,
the vector is high-dimensional but typically very spars
(Banerjee and al, 2005). For every movie in this
dataset, the corresponding genre information is ex-
3
cf. http://www.grouplens.org/node/76.
tracted from the Internet Movie Database (IMDB)
collection. If each genre is considered as a sepa-
rate category or cluster, then this dataset has naturally
overlapping clusters since many movies are annotated
in IMDB as belonging to multiple genres. For ex-
ample, Aliens movie belongs to three genres: action,
horror and science fiction.
Figure 4: Most significant Eigenvalues on EachMovie
dataset.
Figure 5: 2D plot of EachMovie dataset using the first and
second principal axis obtained with PCA: (a) data in input
space (b) data in feature space.
We extracted a subset from the EachMovie
dataset: 75 movies scattered on three overlapping
clusters as follows: action=21 movies; comedy=26
movies; crime=17 movies; action+crime=11 movies;
and based on age, sex and rate of users we try to find
a category of video. Figure 5 shows the initial dis-
tribution of these movies where overlapping movies
belong to both action and crime genres. When we
map the same movies in a higher feature space, we
don’t perceive a good improvement on movies dis-
tribution because the selected attributes (age, sex and
user rate) can’t easily predict the genre of movie. But,
KERNEL OVERLAPPING K-MEANS FOR CLUSTERING IN FEATURE SPACE
255

we remark that overlapping movies are more easily
detected in feature space and it lays in the surface be-
tween action and crime movies.
To estimate the number of clusters, we built
a Gram matrix using an RBF kernel with σ = 2.
Figure 4 shows the most significant eigenvalues of
the Gram matrix. We get between 3 and 4 signifi-
cant eigenvalues. Known that EachMovie subset is an
overlapping subset, the suitable choice is three clus-
ters.
Table 3: Comparison between OKM and KOKM on Each-
Movie dataset.
Method Precesion Recall F-measure
OKM based
Euclidean distance 0.582 0.827 0.687
KOKM with
RBF kernel 0.594 0.827 0.692
KOKM with
Polynomial kernel 0.628 0.851 0.722
Then, using OKM with Euclidean distance and
KOKM based on an RBF and on a Polynomial ker-
nel, and by fixing the number of cluster to k = 3, we
run each algorithm twenty times (with similar initial-
izations). Table 3 shows the results obtained where
KOKM algorithm with Polynomial kernel gives the
best results. These results confirm the first results ob-
tained on Iris and Ionosphere datasets. KOKM im-
proves overlapping clustering quality and Polynomial
kernel gives the best results on all tested datasets.
5 CONCLUSIONS
We have proposed in this paper the kernel overlapping
k-means clustering algorithm. This algorithm maps
data from input space to a higher dimensional feature
space through the use of a kernel Mercer function and
optimizes an objective function that looks for optimal
clusters in feature space. The main advantages of this
algorithm are its ability to identify nonlinearly sep-
arable clusters in input space and its ability to sepa-
rate clusters with complex boundary. Moreover, we
propose an estimation of the number of clusters us-
ing the Gram matrix. This estimation is based on the
assumption that we must add more clusters when the
overlap between clusters becomes larger. Empirical
results show that KOKM using both Polynomial and
RBF kernels outperforms OKM in terms of precision
recall and F-measure for overlapping clusters and for
non overlapping clusters.
As a future work, we plan to improve this kernel
overlapping k-means algorithm by proposing another
version of KOKM where prototypes and objects im-
ages are computed in feature space. In this way, ker-
nel overlapping clustering can be applied to structured
data, such as trees, strings, histograms and graphs.
REFERENCES
Banerjee, A., Krumpelman, C., Basu, S., Mooney, R., and
Ghosh, J. (2005). Model based overlapping clustering.
In International Conference on Knowledge Discovery
and Data Mining, Chicago, USA. SciTePress.
Ben-Hur, A., Horn, D., Siegelmann, H. T., and Vapnik, V.
(2000). Support vector clustering. In International
Conference on Pattern Recognition, pages 724–727,
Barcelona, Spain.
Bertrand, P. and Janowitz, M. F. (2003). The k-weak hier-
archical representations: an extension of the indexed
closed weak hierarchies. Discrete Applied Mathemat-
ics, 127(2):199–220.
Camastra, F. and Verri, A. (2005). A novel kernel method
for clustering. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 27:801–804.
Cleuziou, G. (2007). Okm : une extension des k-moyennes
pour la recherche de classes recouvrantes. Revue
des Nouvelles Technologies de l’Information, Cpadus-
Edition RNTI-E, 2:691–702.
Cleuziou, G. (2008). An extended version of the k-means
method for overlapping clustering. In International
Conference on Pattern Recognition ICPR, pages 1–4,
Florida, USA. IEEE.
Cleuziou, G. (2009). Okmed et wokm : deux variantes
de okm pour la classification recouvrante. Revue
des Nouvelles Technologies de l’Information, Cpadus-
Edition, 1:31–42.
Deodhar, M. and Ghosh, J. (2006). Consensus cluster-
ing for detection of overlapping clusters in microarray
data.workshop on data mining in bioinformatics. In
International Conference on data mining, pages 104–
108, Los Alamitos, CA, USA. IEEE Computer Soci-
ety.
Diday, E. (1984). Orders and overlapping clusters by pyra-
mids. Technical Report 730, INRIA, France.
Girolami, M. (2002). Mercer kernel-based clustering in fea-
ture space. IEEE Transactions on Neural Networks,
13(13):780–784.
Sch
¨
olkopf, B., Smola, A., and M
¨
uller, K.-R. (1998). Non-
linear component analysis as a kernel eigenvalue prob-
lem. Neural Computation, 10(5):1299–1319.
Zhang, D. and Chen, S. (2002). Fuzzy clustering using ker-
nel method. In International Conference on Control
and Automation, pages 123–127, Xiamen, China.
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
256