A SECURE AND EFFICIENT ORDER PRESERVING ENCRYPTION

SCHEME FOR RELATIONAL DATABASES

Hasan Kadhem

Department of Computer Science,Graduate School of Systems and Information Engineering

University of Tsukuba, Tsukuba, Japan

Toshiyuki Amagasa, Hiroyuki Kitagawa

Department of Computer Science,Graduate School of Systems and Information Engineering

Center for Computational Sciences, University of Tsukuba, Tsukuba, Japan

Keywords:

Order preserving encryption, Known plaintext attack, Statistical attack.

Abstract:

Encryption is a well-studied technique for protecting the conﬁdentiality of sensitive data. However, encrypting

relational databases affects the performance during query processing. Preserving the order of the encrypted

values is a useful technique to perform queries over the encrypted database with a reasonable overhead. Un-

fortunately, the existing order preserving encryption schemes are not secure against known plaintext attacks

and statistical attacks. In those attacks, it is assumed that the attacker has prior knowledge about plaintext

values or statistical information on the plaintext domain.

This paper presents a novel database encryption scheme called MV-POPES (Multivalued - Partial Order Pre-

serving Encryption Scheme), which allows privacy-preserving queries over encrypted databases with an im-

proved security level. Our idea is to divide the plaintext domain into many partitions and randomize them in

the encrypted domain. Then, one integer value is encrypted to different multiple values to prevent statistical

attacks. At the same time, MV-POPES preserves the order of the integer values within the partitions to allow

comparison operations to be directly applied on encrypted data. Our scheme is robust against known plaintext

attacks and statistical attacks. MV-POPES experiments show that security for sensitive data can be achieved

with reasonable overhead, establishing the practicability of the scheme.

1 INTRODUCTION

Encryption is a well-studied technique to protect sen-

sitive data so that when a database is compromised

by an intruder, data remains protected even when a

database is successfully attacked or stolen. Recogniz-

ing the importance of encryption techniques, several

database vendors offer an integrated solution that pro-

vides standard encryption functionality in their prod-

ucts. Even though encrypting the database provides

important protection, performing queries over the en-

crypted databases becomes more challenging. En-

crypting database using a standard block cipher such

as AES, and DES causes undesirable performance

degradation during query processing. The reason is

that the standard encryption techniques do not pre-

serve the order of integers, so an entire table scan

would be needed to perform queries such as range

query. Thus the query execution can become unac-

ceptably slow.

Preserving the order of the encrypted values is a

useful technique to perform quires over the encrypted

database with a reasonable overhead. For instance,

given three integers {a,b,c}, such that (a<b<c), then the

encrypted values are (E

(a)<E

(b)<E

(c)). Here, E

(v)

denotes ciphertext value of v with encryption key K.

The order preserving encryption scheme OPES pro-

posed ﬁrstly by (Agrawal et al., 2004). The idea of

OPES is to take as input a user-provided target dis-

tribution and transform the plaintext values in such a

way that the transformation preserves the order while

the transformed values follow the target distribution.

The strength and novelty of OPES is that comparison

operations, equality and range queries as well as ag-

gregation queries involving MIN, MAX and COUNT

can be evaluated directly on encrypted data, with-

Kadhem H., Amagasa T. and Kitagawa H..

A SECURE AND EFFICIENT ORDER PRESERVING ENCRYPTION SCHEME FOR RELATIONAL DATABASES.

DOI: 10.5220/0003095700250035

In Proceedings of the International Conference on Knowledge Management and Information Sharing (KMIS-2010), pages 25-35

ISBN: 978-989-8425-30-0

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

out decryption. Another encryption scheme proposed

by (Chung and Ozsoyoglu, 2006; Ozsoyoglu et al.,

2003), where a sequence of polynomial functions is

used to encrypt integer values while preserving the or-

der. The decryption is made by solving the inverses of

each polynomial function in the sequence in reverse

order.

Unfortunately, the previous order preserving en-

cryption (OPE) schemes are not secure against known

plaintext attacks and statistical attacks. In those at-

tacks, it is assumed that the attacker has a prior knowl-

edge about plaintext values or statistical information

on plaintext domain. The authors of the previous

OPE schemes either ignore those type of attacks oras-

sumed that the attacker does not have any information

about the plaintext domain. In reality, the attacker in

many cases may have general or advanced informa-

tion about plaintext domain. Here, the attacker who

has access to the encrypted values and has knowledge

about the plaintext can map both the plaintext and the

encrypted values and make use of them to obtain the

key. This is because the OPE schemes preserve the

order of all integers in the domain, so the order of en-

crypted values is exactly the order of plaintext values

(we called those schemes as full OPE).

This paper presents a new database encryption

scheme called MV-POPES (Multivalued - Partial Or-

der Preserving Encryption Scheme), which divide the

plaintext domain into many partitions and randomize

them in the encrypted domain. It allows one integer to

be encrypted to many values using the same encryp-

tion key while preserving the order of the integer val-

ues within the partitions. Here, still we can get ben-

eﬁt from the partial order preserving in the encrypted

data to perform queries directly at the server without

decrypting data. At the same time, it prevents attack-

ers from inferring individual information from the en-

crypted database even if they have statistical and spe-

cial knowledge about the plaintext database. The rea-

son is that the encrypted values are totally in different

order compared with the plaintext values. The results

from an implementation of MV-POPES show that se-

curity for sensitive data can be achieved with reason-

able overhead, establishing the practicability of the

scheme.

Our threat model is same as the one in the pre-

vious OPE schemes (Agrawal et al., 2004) but with

more conservative approach. We assume that the at-

tacker not only has access to the encrypted database

ﬁles but also has special knowledge about the plain-

text database. However, the attacker does not have

access to the logs and the memory of the database

software. Figure 1 shows the system model where

the client sends a rewritten query using the metadata

Encrypted Database

Decrypt

Result

Rewrite

Query

Client

Metadata

Database Software

compile query and execute over

encrypted database

Figure 1: System model.

to the database software. Then the query is executed

on the encrypted database and return the results to

the client who decrypt them using same metadata.

The metadata, query rewriting, and result decryption

could be on the database software or on client side. In

this paper we consider them to be on client side. We

make the following contributions:

• We analyze the security of previous full OPE

schemes based on an attack model we deﬁne, con-

sisting of known plaintext attack and statistical at-

tack (Section 2).

• We propose our novel database encryption

scheme (MV-POPES) and the metadata used to

support encryption, decryption and efﬁcient query

processing (Section 3).

• We explain how to translate a query condition

over a plaintext to corresponding conditions over

encrypted database (Section 4).

• We show how relational operators can be imple-

mented efﬁciently over encrypted relations (Sec-

tion 5).

• We analyze the security of our scheme based on

deﬁnitions and theorems we deﬁne in Section 2

(Section 6).

• We complement our analytical results with experi-

ments on differentdomains that measure the effect

of our encryption scheme on query processing ef-

ﬁciency, as well as the client post processing cost

(Section 7).

The related work is discussed in Section 8. We con-

clude with a summary and directions for future work

in Section 9.

2 SECURITY ISSUES

In this section we analyze the security of the full OPE

schemes based on two concepts, the mapping proba-

bility and similarity degree of statistics.

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

2.1 Mapping Probability

The mapping probability is related to the known

plaintext attack. In this attack, it is assumed that the

attacker has both the plaintext and its encrypted ver-

sion (ciphertext) and makes use of them to obtain the

key used in the encryption process.

Deﬁnition 1. (Mapping Probability (µ)) Let ε be an

encryption scheme. Let ρ be the set of plaintext values

and ς be the corresponding set of ciphertext values

using ε. Let η be the number of possible mappings

between ρ and ς. Then, the mapping probability µ is

the probability to pickup the correct mapping among

η, so µ = 1/η.

Theorem 1. (Security against Known Plaintext At-

tack) Let ε be an encryption scheme. Let µ be the

mapping probability between the set of plaintext val-

ues ρ and the corresponding set of ciphertext values

ς using ε. Then, ε is secure against known plaintext

attack when µ is signiﬁcantly small.

Note that the µ will be signiﬁcantly small if η is

exponentially large. This theorem shows that by hav-

ing large η, it will be almost impossible for the at-

tacker to infer information about encryption scheme

and the key by the advantage of knowing both plain-

text and cipher text values.

Using a full OPE scheme, we can clearly see that

there is only one possible mappings (η = 1) between

ρ and ς, then µ = 1. The reason is that both the plain-

text and ciphertext values have exactly the same order.

So any full OPE scheme is not secure against known

plaintext attack.

2.2 Similarity Degree of Statistics

The Similarity Degree of Statistics is related to the

statistical attack. In this attack, the attacker tries to

ﬁnd a match between the ciphertext values and plain-

text values based on some statistical information on

plaintext and make use of them to obtain the key.

Deﬁnition 2. (Similarity Degree of Statistics (∆)) Let

ε be an encryption scheme. Let Σ

be the statistics on

plaintext values and Σ

be the statistics on the cor-

responding ciphertext values using ε. Then, ∆ is the

percentage of similarity between both Σ

and Σ

The statistics here involvingfrequencies of values,

and aggregation functions such us MIN, MAX, SUM,

and COUNT.

Theorem 2. (Security against Statistical Attack) Let

ε be an encryption scheme. Let ∆ be the Similarity

Degree of Statistics between the statistics on plaintext

and the statistics on the corresponding ciphertext

using ε. Then, ε is secure against statistical attack

when ∆ is signiﬁcantly small.

Using a full OPE scheme, the aggregation func-

tion such as MIN, MAX, and COUNT are exactly the

same on both plaintext and ciphertext values. In addi-

tion, many previous full OPE schemes encrypt plain-

text value to another ﬁxed value, so the frequencies of

values are same before and after encryption. The re-

sult will be high similarity degree of statistics ∆ which

means that the full OPE scheme is not secure against

statistical attack.

3 RELATIONAL ENCRYPTION

This section describes our encryption scheme in de-

tail.

3.1 An Overview of MV-POPES

When encrypting plaintext values in a column hav-

ing values in the range [D

min

max

], ﬁrst, we divide the

domain into n partitions and assign for each partition

a random number from 1 to n. This number will be

the order of partitions in the encrypted domain. We

change the order of partitions to hide the original or-

der of plaintext values. Then, we generate boundaries

for all integers in all partitions using an order preserv-

ing function. We preserve the order within the parti-

tion to be able to evaluate queries efﬁciently on en-

crypted database. The generated boundaries identify

the intervals. For instance, interval I

is identiﬁed by

i+1

). We then generate the encrypted values for in-

teger i as random values from the interval I

, so one

plaintext value is encrypted to many different values.

This will change the frequencies of the plaintext val-

ues to prevent the encrypted database against statisti-

cal attack.

3.2 Partitioning and Metadata

Here, we explain the partitioning function for each at-

tribute’s domain and what is stored in the metadata

for each domain. We ﬁrst divide the plaintext domain

of values [D

min

max

] into partitions {p

,...,p

}, such that

these partitions cover the whole domain and there is

no overlap between them. Then, we assign for each

partition a unique random number in the range of [1,n].

This number is the new order of partitions in the en-

crypted domain.

As an example, Figure 2 shows the partitions

metadata for the domain [1,100]. The domain is divided

into 5 partitions: [1,20],[21,40],[41,60],[61,80],[81,100]. (F), (L)

A SECURE AND EFFICIENT ORDER PRESERVING ENCRYPTION SCHEME FOR RELATIONAL DATABASES

PID EPID PREV F L NEXT

1 3 80 1 20 81

2 1 - 21 40 61

3 5 100 41 60 101

4 2 40 61 80 1

5 4 20 81 100 41

Figure 2: Partitioning metadata.

are the ﬁrst and last number in the partition. The par-

tition identiﬁer (PID) represents the original order of

partitions in plaintext domain. The encrypted parti-

tion identiﬁer (EPID) represents the order of partition

in the encrypted domain. (PREV) and (NEXT) are the

previous and the next number in the encrypted domain

for a partition. For instance, the partition [61,80] where

PID=4, and EPID=2, the (PREV) will be the last number

for the partition with EPID=1 (which is 40), and the

(NEXT) will be the ﬁrst number for the partition with

EPID=3 (which is 1).

The metadata is used to generate bucket bound-

aries, encryption/decryption and query translation. It

contains all the secret information about partitions so

must be a well-kept secret, as well as the key.

3.3 Generation of Bucket Boundaries

Any order preserving function with suitable security

properties can be used to generate the bucket bound-

aries for all integers in the plaintext domain based on

the encrypted order of partitions. Here, we propose

an order preserving function based on secret variables

and a sequence of random numbers.

We are given a domain [D

min

max

], with (D

max

−D

min

1) integers: {D

min

min+1

,...,D

max

}. Initially, we choose

the starting (initial) point from the domain. We then

compute the boundary for the initial point using the

following function:

initial

=Enc

(initial)

where Enc is the function used to encrypt the (initial)

value using key K. Any block cipher algorithm such as

DES (DES, 1977), TDES, Blowﬁsh (Schneier, 1994),

AES (AES, 2001), RSA (Rivest et al., 1978), or a

hashing function can be used to encrypt the value.

To preserve the order of the integers, we use two

functions to generate boundaries. First, boundaries

for values greater than the initial point are gener-

ated by an increasing function. Second, a decreas-

ing function is used to generate boundaries for values

less than the initial point. The goal for the increas-

ing/decreasing function is to create encrypted inter-

val scales for all integers in the domain with differ-

ent sizes. Differences in intervals size are ensured

by predeﬁned percentage and a sequence of random

numbers.

Given the initial point (initial), the interval size IS,

100

101

100

……….. …………… ……….. ………..

………..

a) Plaintext domain.

b) Encrypted domain.

Figure 3: Plaintext domain and the boundaries in the en-

crypted domain.

and the difference percentage on the encrypted inter-

val size DP, the boundaries are derived by the follow-

ing function:

(

i+1

−Enc

(IS)(1+DP∗R

), D

min

≤i<initial

i−1

+Enc

(IS)(1+DP∗R

), initial<i≤D

max+1

where R

is a sequence of random numbers in the range

[−1,1]. There are many pseudorandom number gener-

ators with useful security properties (Blum and Mi-

cali, 1984; Menezes et al., 1996). The DP used in the

formula to control the differences between intervals

size that will be in the range [−Enc

(IS)∗DP,Enc

(IS)∗DP].

Note that B

i+1

will be the (NEXT ) when i is the last num-

ber in the partition and B

i−1

will be the (PREV) when i

is the ﬁrst number in the partition. Figure 3 shows the

plaintext domain and the boundaries generated in the

encrypted domain for the metadata shown in Figure

3.4 Encryption Function

Here we discuss how to encrypt a plaintext relation R.

For each tuple t=(A

,...,A

) in R, the encrypted rela-

tion R

stores a tuple:

(E(A

),E(A

),...,E(A

))

where E is the function used to encrypt an attribute

value of the tuple in the relation. The encryption func-

tion E(i) is applied by choosing a random number in

the interval I

, which is identiﬁed by [B

i+1

). Note

that B

i+1

will be the (NEXT) when i is the last number

in the a partition. Using the example shown in Fig-

ure 3, E(81) will be a random number in the interval

) while E(80) will be a random number in the

interval [B

3.5 Decryption Functions

Given the operator E, which encrypts a plaintext value

to many ciphertext values, we deﬁne its inverse op-

erator D, which decrypts the ciphertext value to its

corresponding plaintext value. Simply, the decryp-

tion function D in MV-POPES searches for the inter-

val where the encrypted value is located. Speciﬁcally,

to decrypt an encrypted value C, the decryption func-

tion searches for the closer boundary B

that is greater

than C, then returns the plaintext value, which is the

left boundary p−1. Details about choosing the initial

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

point for generating boundaries, the random distribu-

tions used for choosing encrypted values and decryp-

tion algorithms are given by (Kadhem et al., 2010).

4 CONDITIONS TRANSLATION

This section explains how to translate a query condi-

tion C over a plaintext database in operations (such as

selection and join) to corresponding conditions over

encrypted database C

. We consider query conditions

characterized by the following grammar rules:

• Condition  Attribute θ Value

• Condition  Attribute θ Attribute

• Condition  (Condition ∨ Condition)|(Condition ∧ Condition)

|(⇁ Condition)

where θ is a binary operation in the set {=,<,≤,>,≥}.

4.1 Partition Identiﬁcation Functions

Before we discuss the translation of conditions, let us

ﬁrst deﬁne the necessary functions on the partitions

identiﬁers. Those functions will be used to translate

conditions that contain comparison operations.

Let A be an attribute, v be a value in the domain and

i be a partition identiﬁer. Table 1 shows the partition

identiﬁcation functions. Using the running example,

PID

(50)={1,2} and PID

(50)={4,5}.

Table 1: Partition Identiﬁcation Functions.

PID

set of PID for attribute A

PID

(v) PID to which value v belongs in the

domain of A

PID

(v) set of PID for attribute A that are

less than the partition that contains

PID

(v) set of PID for attribute A that are

greater than the partition that con-

tains v

PID

set of PID for attribute A that are

less than i

PID

set of PID for attribute A that are

greater than i

4.2 Translation of (Attribute θ Value)

Conditions

Attribute = Value: such condition arises in selection

operations. The translation is deﬁned as follows:

A=v  A

BETWEEN B

and (B

v+1

−1)

The BETWEEN condition allows the retrieval of values

within a range of two values (inclusive). Since the

right boundary B

v+1

is not included in the interval (I

the second value in the BETWEEN condition will be

the right boundary minus 1 (B

v+1

−1).

Attribute < Value: such condition arises in selection

operations. Since the MV-POPES preserves the order

of the encrypted values within the partition ( v

→

)<E

), v

and v

belong to the same PID), the

translation of (A<v) is as follows:

∧ A

≥B

F(PID

(v))

)

i∈PID

(v)

≥B

F(i)

∧ A

NEXT(i)

)

where F(i) is the ﬁrst integer in the partition i, and

NEXT(i) is the next integer of the partition i. Simply,

the result contains all encrypted values that are less

than the left boundary (B

) of the interval (I

) within

the partition that contains v. In addition, all partitions

whose PID are less than the partition of v are included

in the result. For example, the translation condition

for the condition (A<55) is:

∧A

≥B

)∨(A

≥B

∧A

)∨(A

≥B

∧A

)

Attribute ≤ Value: The difference between this con-

dition and the previous one is that this condition in-

cludes all the encrypted values for v, in addition to

those values that are less than the left boundary (B

So, instead of (A

), the condition will be (A

v+1

For conditions Attribute > Value and Attribute

≥ Value, translation is the same as the translation of

A<v and A≤v, as described above but in the opposite

direction.

4.3 Translation of (Attribute θ Attribute)

Conditions

When comparing two different attribute values in

query processing, a straightforward approach is to de-

crypt the ciphertext ﬁrst, then compare the plaintext

values, which may lead to performance degradation.

Instead, we try to make it possible to compare cipher-

text without decryption.

In this work, we introduce a calculated distance

MaxDif f , which is the maximum distance (among all

intervals in the domain) between value P in the pri-

mary key table and value F in the foreign key tables.

The idea is to check if a value being compared is con-

tained within the range of [P−MaxDif f,P+MaxDif f ] (in

case of equality), instead of comparing the value with

P’s bucket boundaries. Notice that it may result in a

false positive, which should be eliminated in a post-

processing.

A SECURE AND EFFICIENT ORDER PRESERVING ENCRYPTION SCHEME FOR RELATIONAL DATABASES

MaxDiff

False positive

Figure 4: Overlap in connecting primary key with foreign

key values based on equality condition.

Given a condition (P θ F), such that P and F have

same domain, P is the primary key and F is a foreign

or primary key. The translation for this condition is

discussed next.

P = F: This condition is translated using the MaxDif f

to:

BETWEEN (P

−MaxDif f ) and (P

+MaxDif f )

Here, MaxDif f is used to ensure that all foreign key

values located in same interval are connected to the

related primary key. Intervals differ, so some foreign

key values from neighbor intervals might connect to

false primary keys (false positive). Figure 4 shows

the process for connecting equal values between a pri-

mary key and foreign key. The total number of false

positives (TFP) can be expressed as:

min

∑

i=D

max

|{ f | f ∈F∧(P

−MaxDi f f ≤ f<B

∨B

i+1

≤ f<P

+MaxDi f f )}|

P < F: The translation for this condition can be per-

formed as follow:

i∈PID



≥B

F(i)

∧P

NEXT(i)

)∧(P

)



j∈PID



≥B

F(i)

∧P

NEXT(i)

)∧(F

≥B

F( j)

∧F

NEXT( j)

)



Simply, we check for each partition (i) in the domain,

the values where P<F and include all values in the par-

titions ( j) that PID is greater than the partition (i).

P ≤ F: This condition should be translated in such a

way that all foreign key values that are greater than

or equal to the primary key can be connected to the

related primary key. The translation of this condi-

tion is same as the previous condition but we use

MaxDif f to ensure all equal values are connected to-

gether. So, instead of P

the condition will be

+MaxDif f ) ≤ F

The translation for P > F and P ≥ F is the same

as the translation of P<F and P≤F as described above,

but in the reverse direction.

4.4 Translation of Composite

Conditions

Two composite conditions are translated directly over

the encrypted domain by translating each condition

individually. The translation is given as follows:

C1 ∨ C2  C1

∨ C2

, C1 ∧ C2  C1

∧ C2

The result based on two composite conditions

might contain false positives when at least one con-

dition is from (Attribute θ Attribute). When both condi-

tions are from (Attribute θ Value) the result will be exact.

Note that the translation of comparison operators on

same attribute will be either the union (∪) between

sets of PIDs (in case of C1 ∨ C2) or the intersection (∩)

between sets of PIDs (in case of C1 ∧ C2).

Translation of (⇁Condition) depends on the condi-

tion type. When the condition is in the form of

(Attribute θ Value), the translation is straightforward:

⇁ C  ⇁C

The result based on this condition will be exact

(without any false positives). However, when C is in

the form of (Attribute θ Attribute), this condition (⇁ C) can-

not be translated directly because of the false positive

result. This paper does not discuss this translation.

Neither are conditions that involve more than one at-

tribute and operator discussed.

5 RELATIONAL OPERATORS

This section describes the process of implementing

relational operators (such as selection, projection, and

sorting) in the proposed scheme. The relational oper-

ators are implemented, as much as possible, to be ex-

ecuted over the encrypted database. However, when a

condition of the form (Attribute θ Attribute) is attached to

the operator, the returned answers might contain false

positives. These answers are then ﬁltered in client-

side after decryption to generate the exact result. Be-

yond that, some operators cannot be performed fully

on the encrypted relations. When that happens, a

post process operation is performed on the result af-

ter decryption. We attempt to minimize the amount of

work done in post process operations. Table 2 shows

the implementation of the operators over encrypted

databases. The E on the operators emphasizes the fact

that the operator is to be executed over the encrypted

database. The L

refers to the encrypted attributes.

Query Splitting. We split the computation of a query

Q across the server and the client. The client will use

the implementation of the relational operators to send

part of the query Q

to the server to be executed on

the encrypted database. The second part, which is

client query part Q

, is performed on the decrypted

data. Query splitting is as follows:

op (R)

|{z}

= op

|{z}

(op

)

| {z }

)

where op

refers to operations performed on the client

side, and op

is operations performed on encrypted

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

Table 2: Implementation of the operators over encrypted

databases.

Operator op op

Selection (σ) σ

(R) D(σ

))

Join (⊲⊳) R

⊲⊳

T σ



D(R

⊲⊳

)



Sorting (τ) τ

(R) τ



D(τ

))



Projection (π) π

(R) D(π

))

Grouping and

Aggregation (γ)

(R) γ



D(τ

))



Duplicate

Elimination (δ)

δ(R) δ



D(τ

))



Union (∪) R∪T D(R

∪

) (based on bag)



D(τ

∪

))



(set)

Difference (−) R−T D(τ

))−D(τ

))

relations R

on the server side.

6 SECURITY ANALYSIS

We can prove the security of our scheme against

known plaintext attack and statistical attack by using

the security deﬁnitions and theorems we deﬁned in

Section 2. For m distinct plaintext values and n corre-

sponding distinct ciphertext values using our encryp-

tion scheme. The number of possible mappings (η) in

an order preserving way is determined by the number

of ways of partitioning the set of plaintext values into

k non-empty partitions and the order of partitions in

the encrypted domain. This number is:

η =



n−1

m−1



∑

i=1

(



m−1

i−1



i!)

where

∑

i=1

(



m−1

i−1



i!) is the possible ways to partition-

ing the plaintext domain and the possible orders for

those partitions, and



n−1

m−1



is the possible frequencies

for the ciphertext values compared with the plaintext

values in an order preserving way. We can clearly see

that (η) is exponentially large even for small plain-

text domain, so the mapping probability (µ) is signiﬁ-

cantly small. By ignoring the number of possible par-

titions and their orders which means considering just

the new order for the plaintext values in the encrypted

domain, the number of possible mappings is:

η =



n−1

m−1



Note that the smallest number of η will be in the case

of primary key attribute where n = m. The reason is

that the possible frequencies in such case are 1. How-

ever, still η is large enough (η = m!) because still an

attacker should ﬁgure out the new order of the plain-

text in the encrypted domain. Thus, based on theorem

1, our scheme is secure against the known plaintext

attack because the mapping probability (µ) is signiﬁ-

cantly small in all cases.

In our scheme, it is clear that the frequencies of

encrypted values and plaintext values are different be-

cause one value is encrypted to many different values.

Also, the statistical functions such as MIN, MAX,

SUM are totally different on ciphertext and plaintext

values. Thereby, the statistics on plaintext values Σ

is diverse from the statistics on the corresponding ci-

phertext values Σ

using MV-POPES. Based on theo-

rem 2, MV-POPES is secure against statistical attack

because the similarity degree of statistics (∆) is sig-

niﬁcantly small. Note that the aggregation functions

(MIN, MAX, COUNT) are still evaluated directly on

the encrypted database using the metadata. For exam-

ple, MIN value for a domain will be the minimum en-

crypted value within the ﬁrst partition and MAX value

will be the maximum encrypted value within the last

partition.

7 EXPERIMENTS

This section evaluates the performance of our encryp-

tion scheme. We have conducted many experiments

to examine the validity and effectiveness of the archi-

tecture proposed in this paper. However, because of

space limitations, we will discuss just four sets of ex-

periments.

7.1 Experimental Setup

The experiments were conducted by implementing

MV-POPES on MS SQL Server 2008. The algorithms

were implemented in VB.NET as a client side appli-

cation. The experiments were run using version 3.0

of the Microsoft.Net framework and on a Microsoft

XP workstation with a 2.6 GHz Intel Core 2 pro-

cessor and 3 GB of memory. The results sketched

in this section are the average for at least 10 execu-

tions. The sets of evaluations was performed on dif-

ferent domains {10,10

,10

} and various number

of partitions (small and large number of partitions)

with difference percentage (DP=0.05). The records on

tables picked randomly from a uniform distribution

between D

min

and D

max

. We used eqi-width as parti-

tioning method.

7.2 Performance for Generating

Boundaries

The ﬁrst set of evaluations was performed to examine

the time needed to generate boundaries. The graph

in Figure 5 shows the execution time for generating

boundaries using the ﬁrst integer in the encrypted do-

main as the initial point. The results show that we have

A SECURE AND EFFICIENT ORDER PRESERVING ENCRYPTION SCHEME FOR RELATIONAL DATABASES

0.05

0.1

0.15

0.2

1 2 3 4 5 6 7 8 9 10

Time per boundary (ms)

Number of partitions

100

1000

10000

100000

0.02

0.04

0.06

0.08

0.1

0.12

0.14

100

150

200

250

300

350

400

450

500

Time per boundary (ms)

Number of partitions

10000

100000

a) Small number of partitions. b) Large number of partitions.

Figure 5: Time per boundary (in ms) required to generate

boundaries.

0.1

0.2

0.3

0.4

0.5

0.6

plaintext

AES

Time per tuple (ms)

Number of partitions

100

1000

10000

100000

0.1

0.2

0.3

0.4

0.5

0.6

100

150

200

250

300

350

400

450

500

plaintext

AES

Time per tuple (ms)

Number of partitions

10000

100000

Large

number of partitions.

Small number of partitions.

Figure 6: Time per tuple (in ms) required to insert tuples.

slightly better performance when the domain is large.

That is because the time needed to encrypt initial point

is divided by larger number in case of large domain.

Generally, the number of partitions (both small and

large) does not affect the performance of generating

the boundaries.

7.3 Performance for Encryption

The second set of evaluations studied the encryption

performance in our scheme using different domains

and various numbers of partitions. Also, we com-

pare the performance of our scheme with a database

encrypted using AES. The table holds 100,000 records

picked randomly from a uniform distribution between

min

and D

max

. Figure 6 shows the times for encryp-

tion and inserting values in the tables for different do-

mains. The results show that AES takes the longest

time to insert tuple since the encryption time is much

more than in MV-POPES. The small difference in

time shown in the ﬁgure between plaintext and our

scheme is the cost of encryption. The ﬁgure shows

that this overhead is negligible. Also, ﬁgure 6(a,b)

shows that the encryption cost of our scheme does not

change by increasing the number of partitions.

7.4 Performance for Equijoin

In the equijoin operation, we studied the percentage

of false positives returned by performing a join oper-

ation over encrypted relations. Also, we studied the

overhead on both the server and client sides. Two ta-

bles were used to perform this evaluation. The ﬁrst

1 2 3 4 5 6 7 8 9 10

False positive (%)

Number of partitions

100

1000

10000

100000

100

150

200

250

300

350

400

450

500

False positive (%)

Number of partitions

10000

100000

0.01

0.02

0.03

0.04

0.05

0.06

AES

Time (ms) per tuple

Number of partitions

100

1000

10000

100000

0.01

0.02

0.03

0.04

0.05

0.06

100

150

200

250

300

350

400

450

500

AES

Time (ms) per tuple

Number of partitions

10000

100000

0.005

0.01

0.015

0.02

0.025

AES

Time (ms) per tuple

Number of partitions

100

1000

10000

100000

0.005

0.01

0.015

0.02

0.025

100

150

200

250

300

350

400

450

500

AES

Time (ms) per tuple

Number of partitions

10000

100000

False positive percentage.

) Query execution time in server side.

) Decryption and filtering cost in client side.

Small

Number of

Partitions

Large

Number of

Partitions

Figure 7: Equijoin cost.

table is the primary key table, which contains all in-

tegers in the domain. The second table is the foreign

key table, which holds 100,000 records. The percentage

of false positives shown in Figure 7(a) increases with

the domain size. That results due to the increase in the

overlap between intervals in the encrypted scale when

performing a join operation based on MaxDif f. How-

ever, the false positive percentage is same with small

and large number of partitions. That because the over-

lap between intervals is not related to the number of

partitions. From Figure 7(b), we can easily see that

the time required to perform a join operation on the

server side in our scheme increases according to the

size of domain and its approximately same as the join

operation on the plaintext (PT) database. While the

cost of join operation using AES is much more than

our scheme. This is especially when using large do-

mains (>10

) since the index is essentially unusable

for many operations (including join) which turn into

full table scans (Hsueh, 2008). Figure 7(c) shows the

client side performance to decrypt and ﬁlter the result

returned by performing a join operation on the server

side. The ﬁgure shows that our scheme has only small

overhead on the client side. We also observe that the

time slightly increases as the domain, because of in-

creased false positives. The results show that using

small or large number of partitions does not affect the

overhead on both server and client side. On the other

hand, we can see the performance degradation when

using AES compared with our scheme.

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

0.005

0.01

0.015

0.02

1 2 3 4 5 6 7 8 9 10 PT

Time (ms) per tuple

Number of partitions

100

1000

10000

100000

0.005

0.01

0.015

0.02

100

150

200

250

300

350

400

450

500

Time (ms) per tuple

Number of partitions

10000

100000

0.005

0.01

0.015

0.02

AES

Time (ms) per tuple

Number of partitions

100

1000

10000

100000

0.005

0.01

0.015

0.02

100

150

200

250

300

350

400

450

500

AES

Time (ms) per tuple

Number of partitions

10000

100000

) Query execution time in server side.

) Decryption cost in client side.

Small

Number of

Partitions

Large

Number of

Partitions

Figure 8: Range query.

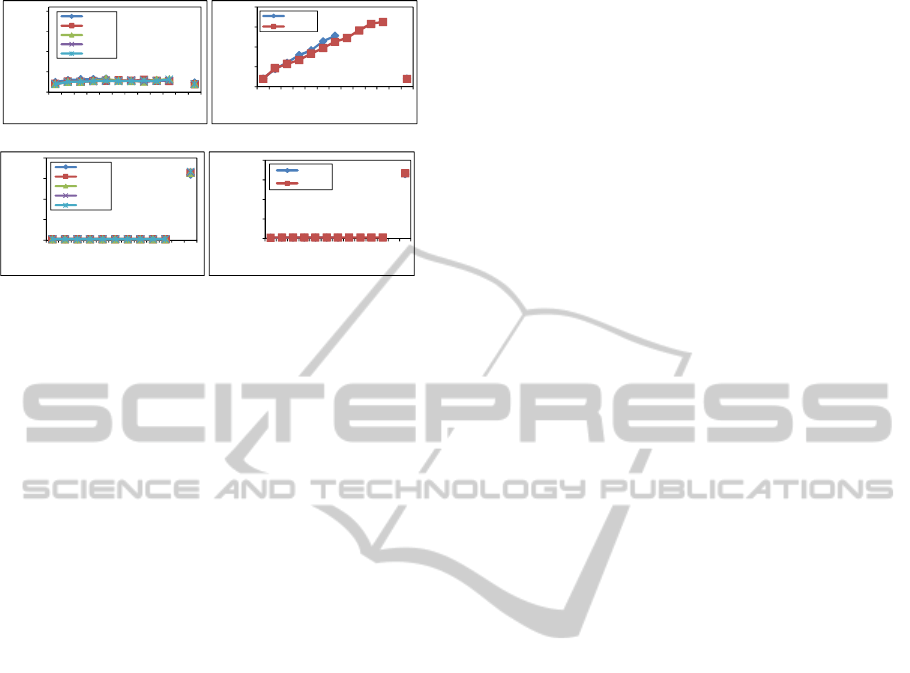
7.5 Performance for Range Query

The last sets of experiments studied the performance

of range queries on MV-POPES. The query used in

those experiments is retrieving all records that are

greater than (domain size/2). Figure 8(a) shows the range

query execution times on plaintext, MV-POPES, and

AES. The ﬁgure illustrates that query response time is

approximately the same in plaintext and our scheme

by using small number of partitions. In our scheme,

using large number of partitions will cause more over-

head on server side because the condition becomes

more complicated. However, we think that the over-

head on server side can be optimized by simplifying

the translated condition. We will investigate that in

details in future work. Figure 8(b) shows the decryp-

tion cost on client side using MV-POPES. We can

see clearly that the decryption overhead is small and

approximately ﬁxed in our scheme using small and

large number of partitions. The Figure also shows

the time required to perform same range query on the

database encrypted using AES. Here the time repre-

sents the decryption time and the time for performing

the range query on the decrypted data. That is because

the range query cannot be executed over the databases

encrypted using AES. Using AES, range query takes

much more time than our scheme on the client side

because of decryption cost.

8 RELATED WORK

Many full OPE schemes (Agrawal et al., 2004; Chung

and Ozsoyoglu, 2006; Ozsoyoglu et al., 2003; Wang

and Lakshmanan, 2006) have been proposed, but no

work discussed the security of the encryption schemes

against known plaintext attack and statistical attack.

Only (Wang and Lakshmanan, 2006) considered the

frequency-based attack which is part of statistical at-

tack in their encryption scheme. (Wang and Lak-

shmanan, 2006) proposed a new encryption scheme

(Order preserving encryption with splitting and scal-

ing (OPESS)) based on the OPES to index the en-

crypted values in the outsourced XML databases. The

idea in OPESS is to map the same plaintext values to

different ciphertext values to protect the data against

frequency-based or statistical attacks. However, this

scheme still preserve the order for all encrypted val-

ues so it is possible to estimate at least the top and

bottom parts of the plaintext domain. One of the lim-

itations of OPESS is that security achieved by scaling

encrypted data causes an increase in data size. Also,

this approach is not efﬁcient in insertions and updates

becausehe encryption method is mainly based on the

number of occurrences. OPESS proposed mainly for

XML database but it is not applicable for relational

database. The reason behind that is the different

in executing queries on the relational and the XML

databases such as the join operation between differ-

ent encrypted values.

The bucketing approach (Hore et al., 2004;

Hacig¨um¨us¸ et al., 2002) is closely related to our

scheme in sense of dividing the plaintext domain into

many partitions (buckets). The encrypted database

is augmented with additional information (the index

of attributes), thereby allowing query processing to

some extent at the server without endangering data

privacy. The encrypted database in the bucketing ap-

proach contains etuples (the encrypted tuples) and

corresponding bucket-ids (where many plaintext val-

ues are indexed to same bucket-id). In this scheme,

executing a query over the encrypted database is

based on the index of attributes. The result of this

query is a superset of records containing false positive

tuples. These false hits must be removed in a post ﬁl-

tering process after etuples returned by the query are

decrypted. Because only the bucket id is used in a join

operation, ﬁltering can be complex, especially when

random mapping is used to assign bucket ids rather

than order preserving mapping. The number of false

positive records depends on the number of buckets in-

volved. Using a small number of buckets will hide the

real values within the bucket index, but the ﬁltering

overhead can become excessive. On the other hand, a

large number of buckets will reduce the ﬁltering over-

head, but the scheme will be vulnerable to estimation

exposure. In bucketing, the projection operation is not

implemented over the encrypted database, because a

row level encryption is used. In addition, updating at-

tributes in the bucketing approach requires that two

attributes be updated, the bucket-id and the etuple.

This means that all attributes in the row must be re-

A SECURE AND EFFICIENT ORDER PRESERVING ENCRYPTION SCHEME FOR RELATIONAL DATABASES

encrypted, thereby increasing overhead for the update

query.

Many researchers have investigated the problem

of keywords searching on encrypted data using either

symmetric encryption (Song et al., 2000), asymmet-

ric encryption (Boneh et al., 2004) or a combination

of symmetric, asymmetric encryption and hash func-

tions (Dong et al., 2008). In spite of security vul-

nerabilities (like statistical attack (Song et al., 2000))

and signiﬁcant overhead (Boneh et al., 2004; Dong

et al., 2008), these encryption schemes are possibly

useful in searching for keywords in a ﬁle, document

or email. However, these solutions can not be applied

to the problem of efﬁciently querying encrypted re-

lational databases. Especially, we discuss in this pa-

per the problem of encrypting integer data, executing

range queries and implementing relational operations

over encrypted database.

9 CONCLUSIONS

We propose a novel order preserving encryption

scheme (MV-POPES) that is robust against known

plaintext attack and statistical attack. In MV-POPES,

we change the order of the plaintext values by por-

tioning the domain into many partitions and assign a

unique random number to each partition that repre-

sents the order in the encrypted domain. MV-POPES

allows one integer to be encrypted to many different

values using the same encryption key. It also pre-

serves the order of the integer values within each par-

tition to allow comparison operation to be directly

applied to the encrypted data. We have developed

techniques so that most processes in executing SQL

queries can be done on encrypted databases. In some

cases, a small amount of work to ﬁlter false positives

or perform relational operations is needed on the de-

crypted data. Experiments on MV-POPES showed

that security for sensitive data can be achieved with

reasonable overhead, conﬁrming the feasibility of the

scheme. In the future, we will investigate the opti-

mal algorithm for domain partitioning that minimize

performance overhead in query processing and ensure

high privacy. We also plan to study the encryption of

non-integer data such as strings.

ACKNOWLEDGEMENTS

This research has been supported in part by the

Graint-in-Aid for Scientiﬁc Research from MEXT

(#21013004) and Grant-in-Aid for Young Scientists

(B) (#21700093) by JSPS.

REFERENCES

AES (2001). Advanced encryption standard. National In-

stitute of Science and Technology, FIPS 197.

Agrawal, R., Kiernan, J., Srikant, R., and Xu, Y. (2004).

Order preserving encryption for numeric data. In

SIGMOD ’04: Proceedings of the 2004 ACM SIG-

MOD international conference on Management of

data, pages 563–574, New York, NY, USA. ACM.

Blum, M. and Micali, S. (1984). How to generate crypto-

graphically strong sequences of pseudo-random bits.

SIAM J. Comput., 13(4):850–864.

Boneh, D., Crescenzo, G. D., Ostrovsky, R., and Per-

siano, G. (2004). Public key encryption with key-

word search. In EUROCRYPT 2004: Proceedings

of International Conference on the Theory and Appli-

cations of Cryptographic Techniques, pages 506–522.

Springer.

Chung, S. S. and Ozsoyoglu, G. (2006). Anti-tamper

databases: Processing aggregate queries over en-

crypted databases. In ICDEW ’06: Proceedings of

International Conference on Data Engineering Work-

shops, page 98, Washington, DC, USA. IEEE Com-

puter Society.

DES (1977). Data encryption standard. Federal Information

Processing Standards Publication, FIPS PUB 46.

Dong, C., Russello, G., and Dulay, N. (2008). Shared

and searchable encrypted data for untrusted servers.

In Proceeedings of the 22nd annual IFIP working

conference on Data and Applications Security, pages

127–143, Berlin, Heidelberg. Springer-Verlag.

Hacig¨um¨us¸, H., Iyer, B., Li, C., and Mehrotra, S. (2002).

Executing SQL over encrypted data in the database-

service-provider model. In SIGMOD ’02: Proceed-

ings of the 2002 ACM SIGMOD international confer-

ence on Management of data, pages 216–227, New

York, NY, USA. ACM.

Hore, B., Mehrotra, S., and Tsudik, G. (2004). A privacy-

preserving index for range queries. In VLDB ’04: Pro-

ceedings of the 30th international conference on Very

large databases, pages 720–731. VLDB Endowment.

Hsueh, S. (February 2008). Database encryption in SQL

server 2008 enterprise edition. Microsoft White Pa-

pers, SQL Server 2008.

Kadhem, H., Amagasa, T., and Kitagawa, H. (2010).

MV-OPES: Multivalued - order preserving encryption

scheme: A novel scheme for encrypting integer value

to many different values. IEICE Transactions, 93-

D(9):accepted.

Menezes, A. J., Vanstone, S. A., and Oorschot, P. C. V.

(1996). Handbook of Applied Cryptography. CRC

Press, Inc., Boca Raton, FL, USA.

Ozsoyoglu, G., Singer, D. A., and Chung, S. S.

(2003). Anti-tamper databases: Querying encrypted

databases. In 17th Annual IFIP Working Conference

on Database and Applications Security, Estes Park,

pages 4–6.

KMIS 2010 - International Conference on Knowledge Management and Information Sharing

Rivest, R. L., Shamir, A., and Adleman, L. (1978). A

method for obtaining digital signatures and public-key

cryptosystems. Commun. ACM, 21(2):120–126.

Schneier, B. (1994). Description of a new variable-

length key, 64-bit block cipher (Blowﬁsh). In Fast

Software Encryption, Cambridge Security Workshop,

pages 191–204, London, UK. Springer-Verlag.

Song, D. X., Wagner, D., and Perrig, A. (2000). Practical

techniques for searches on encrypted data. In SP’00:

Proceedings of the 2000 IEEE Symposium on Security

and Privacy, page 44, Washington, DC, USA. IEEE

Computer Society.

Wang, H. and Lakshmanan, L. V. S. (2006). Efﬁcient se-

cure query evaluation over encrypted XML databases.

In VLDB ’06: Proceedings of the 32nd international

conference on Very large databases, pages 127–138.

A SECURE AND EFFICIENT ORDER PRESERVING ENCRYPTION SCHEME FOR RELATIONAL DATABASES