HIGHER-ORDER REPRESENTATION AND REASONING FOR

AUTOMATED ONTOLOGY EVOLUTION

Michael Chan, Jos Lehmann and Alan Bundy

School of Informatics, University of Edinburgh, 10 Crichton Street, Edinburgh, U.K.

Keywords:

Ontology, Automated ontology evolution, Ontology conﬂict detection, Higher-order logic, Ontology repair

plans, Isabelle/HOL, Development graphs, GALILEO.

Abstract:

The GALILEO system aims at realising automated ontology evolution. This is necessary to enable intelligent

agents to manipulate their own knowledge autonomously and thus reason and communicate effectively in open,

dynamic digital environments characterised by the heterogeneity of data and of representation languages. Our

approach is based on patterns of diagnosis of faults detected across multiple ontologies. Such patterns allow

to identify the type of repair required when conﬂicting ontologies yield erroneous inferences. We assume that

each ontology is locally consistent, i.e. inconsistency arises only across ontologies when they are merged

together. Local consistency avoids the derivation of uninteresting theorems, so the formula for diagnosis can

essentially be seen as an open theorem over the ontologies. The system’s application domain is physics;

we have adopted a modular formalisation of physics, structured by means of locales in Isabelle, to perform

modular higher-order reasoning, and visualised by means of development graphs.

1 INTRODUCTION

Artiﬁcial intelligence and, more generally, computer

science are presently faced with the challenge that au-

tonomous software agents must be able to manipulate

their own knowledge. Such knowledge is typically

represented in an ontology that conceptualises the en-

tities of the software’s application domain and allows

the software to reason about such entities at a higher

level of abstraction than simply the level of data or

information. Just like any abstract model, ontologies

are limited representations of the world, which is dy-

namic and inherently complex. If autonomous sys-

tems are to deal with such dynamics, they must be

able to autonomously update their own ontologies.

The process of updating an ontology in the face

of new information is often called ontology evolu-

tion. The literature on the subject mostly concentrates

on the evolution of ontologies coded in Description

Logic for Semantic Web applications (Bundy et al.,

2009). The primary accent is on deﬁning logical no-

tions and/or methods to enable a user to maintain the

consistency of an ontology either through its lifecy-

cle or in relation to other ontologies. The former

case is often related to ontology debugging and yields

notions like conservative extensions (Ghilardi et al.,

2006), belief revision (Katsuno and Mendelzon,

1991) interactive ontology evolution (Stojanovic

et al., 2002), inconsistency repair (Kalyanpur

et al., 2006; Lam et al., 2008; Ovchinnikova and

uhnberger, 2007). The case of multiple ontolo-

gies is often related to ontology alignment and yields

notions like mapping (Kalfoglou and Schorlemmer,

2003), matching (Doan et al., 2004; Giunchiglia and

Shvaiko, 2004), or contextualisation. Despite these

valuable research efforts on the dynamics of ontolo-

gies, we know of relatively few works that have

explicitly considered the problem of applying auto-

mated mechanisms to repair locally consistent but

globally inconsistent ontologies. In this type of sit-

uations belief revision may be insufﬁcient to resolve

conﬂicts between ontologies and the very signature of

their representation language may need to be evolved.

This opens up many kinds of syntactical manipula-

tions, including splitting a function into parts and

changing the arity of a function. An attempt at this

kind of automated ontology evolution is described in

(McNeill and Bundy, 2007), which investigates an en-

vironment in which agents with slightly different on-

tologies interact with each other. The main goal of the

described system, the GALILEO System, is to iden-

tify and repair ontological mismatches arising from

the heterogeneity in the underlying logical represen-

tation, e.g., arity mismatches.

Chan M., Lehmann J. and Bundy A..

HIGHER-ORDER REPRESENTATION AND REASONING FOR AUTOMATED ONTOLOGY EVOLUTION.

DOI: 10.5220/0003097800840093

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 84-93

ISBN: 978-989-8425-29-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

In our view the limited progress in automated on-

tology evolution described above depends on two cir-

cumstances. On the one hand, most of the works ad-

dress interactive ontology evolution driven by user’s

instructions. This choice is a pragmatic one, dic-

tated by the need to support ontology developers in

their work, rather than by a quest for automation. In

many cases, though, that is not enough because what

is actually required is ontology evolution at runtime

performed, for instance, by autonomous agents that

communicate with each other in heterogeneous envi-

ronments, including the Semantic Web. On the other

hand, the focus on ontologies coded in Description

Logics does not allow for a sufﬁciently generic analy-

sis and resolution of ontological inconsistencies, even

when an approach aims at automating, for instance,

the integration of changes in ontologies. As a mat-

ter of fact, the limited expressivity of ﬁrst-order or

lesser logics constitutes a limit on the possibility of

modelling the ontology evolution process in the same

language in which the ontology is coded. Being im-

possible to quantify over, and thus, to reason about,

the predicates, the relations and the functions of the

ontology, it is very problematic to formalise and im-

plement a sufﬁciently generic ontology evolution pro-

cess.

We therefore turned to study automated (as op-

posed to user-assisted) ontology evolution using

higher-order logic (HOL), which provides the ben-

eﬁt of making it possible to express sufﬁciently

generic patterns of evolution. In the framework of

the GALILEO system (Bundy and Chan, 2008; Chan

and Bundy, 2008), a number of so-called ontology

repair plans (ORPs) are being developed and imple-

mented in HOL. These mechanisms compile together

patterns for diagnosis of conﬂicts between ontologies

and transformation rules for effecting repairs. For

both development and testing, we rely on examples

of ontology evolution in physics. Many seminal ad-

vances in physics are results of ontology evolution, as

physicists revise predictive theories when confronted

with conﬂicting experimental evidence. Therefore, in

ORPs developed thus far, one of the ontologies rep-

resents a predictive theory; a second ontology repre-

sents a sensory or experimental set-up for that the-

ory. When the sensory ontology generates a theorem

that contradicts a theorem of the theoretical ontology,

an ORP is triggered and amends the two ontologies.

ORPs may act either as belief revision mechanisms or

as signature revision mechanisms or both. Working

in HOL provides the additional beneﬁt of formalising

concepts and their relationships with a highly expres-

sive representation. We believe this is desirable, be-

cause physics concepts are often naturally represented

Suppose we have an ontology O

representing the cur-

rent state of a predictive physics theory and an ontol-

ogy O

representing some sensory information arising

from an experiment. Suppose these two ontologies

disagree over the value of some function stuff when it

is applied to a vector of arguments

s of type

τ. stuff (

might, for instance, be the total energy of a ball or the

orbit of a planet.

Trigger: If stuff (

s) has two different values in O

and

then the following formula will be triggered,

identifying a potential contradiction between the-

ory and experiment.

` stuff (

s) = v

(1)

` stuff (

s) = v

(2)

` v

6= v

(3)

where O ` φ means that formula φ is a theorem of

ontology O.

Figure 1: Trigger of the “Where’s My Stuff?” ontology

repair plan.

as HOL objects, e.g., the orbit of a star, the rate of

change in a quantity, etc.

In this paper we discuss the diagnostic mech-

anism of the ORP called Where’s my stuff? (WMS)

(Bundy and Chan, 2008). WMS is triggered when the

predicted value returned by a function, which we call

stuff , conﬂicts with the observed value of the same

function. The trigger formulae of WMS are formalised

in Figure 1. The purpose of WMS is to amend the

signature of two conﬂicting ontologies by redeﬁning

the function that computes the quantity that is sub-

ject to contradiction and that instantiates the higher

order variable stuff . In practice, WMS deploys an

addition-strategy that is quite common in physics.

For instance, in order to account for unpredictable

yet observed gravitational behaviours in the orbit of

a planet or in the stellar orbital velocity in a galaxy,

astronomers often postulate the presence of an addi-

tional unobserved planet or, resp., of dark matter. Ac-

cordingly, WMS redeﬁnes the contradictory function

(in the examples, the functions orbit, resp., orbital ve-

locity) as the sum of a visible part (i.e. the amount

calculated by the original function) and an invisible

part (i.e. the amount that can only indirectly be ob-

served). For WMS’s repair operation to be triggered,

its diagnostic mechanism must have individuated the

function stuff and assessed a contradiction between

the value of stuff in the theoretical and the sensory

ontologies.

HIGHER-ORDER REPRESENTATION AND REASONING FOR AUTOMATED ONTOLOGY EVOLUTION

The workings of such diagnosis allow us to illus-

trates two points about using a higher-order approach

for ontology evolution:

1. The polymorphism of stuff , as well as of other

symbols like =, 6=, <, −, etc. permits the gen-

erality of WMS and its applicability over disparate

cases.

2. The use of a higher-order theorem prover like Is-

abelle (Paulson, 1994), allows reasoning over lo-

cally consistent but globally inconsistent ontolo-

gies that share variables.

More strongly, these two points are important re-

sults for both ontology evolution and automated theo-

rem proving, and they represent the main contribution

of this paper. They show that current interactive the-

orem proving technology is capable of inferring the

trigger formulae used in ontology repair plans, despite

their problematic features described above.

The rest of the paper is structured as follows: §2

gives an overview of two examples of ontology evolu-

tion in physics that are used in subsequent sections to

evaluate the proposed approach to the representation

and reasoning for ontology evolution; §3 describes

the structure of the ontological representation and the

speciﬁc axioms of the theoretical and sensory ontolo-

gies; and, §4 highlights the advantages of detecting

conﬂicts between ontologies using HOL. Note that

details of ontology repair procedures are not covered

in this paper; we refer interested readers to (Bundy

and Chan, 2008; Chan and Bundy, 2008) for more

complete presentations.

2 TWO EXAMPLES OF

ONTOLOGY EVOLUTION IN

PHYSICS

In this paper, we base our evaluation of the represen-

tation of knowledge and reasoning on two examples

of ontology evolution in physics: the bouncing-ball

paradox and the proposed existence of dark matter.

Both cases can be emulated by WMS.

The bouncing-ball paradox, as described in

(diSessa, 1983), involves dropping a ball from a

height above ground and calculating its total energy

as the sum of its kinetic energy, which is a function of

the ball’s velocity, and of its potential energy, which

is a function of its height on the ground. The initial

amount of total energy of the ball is greater than zero

because of its positive amount of potential energy. If

the amount of total energy is deﬁned as a summation

of kinetic and potential energies, the ﬁnal amount of

total energy of the ball will then be zero Joules be-

cause of its zero velocity and zero height at ground

level. The paradox is exactly the contradiction be-

tween the initial and ﬁnal amounts of total energy of

the ball: the law of conservation of energy requires

such amounts to be the same. WMS emulates the usual

solution to the paradox and adds to the function that

computes the total energy of the ball a third compo-

nent, for elastic energy. This is the type of energy

to which the ball’s kinetic energy is transformed at

the time of impact with the ground. This solution is

equivalent to re-idealising the ball as a spring rather

than as a particle.

In the case of the hypothetic existence of dark mat-

ter, the evidence for it comes from various sources,

for instance, from an anomaly in the orbital veloc-

ities of stars in spiral galaxies identiﬁed by Rubin

in 1975. Given the observed distribution of mass in

these galaxies, we can use Newtonian Mechanics to

predict that the orbital velocity of each star should

be inversely proportional to the square root of its

distance from the galactic centre (called its radius).

However, observation of these stars show their orbital

velocities to be roughly constant and independent of

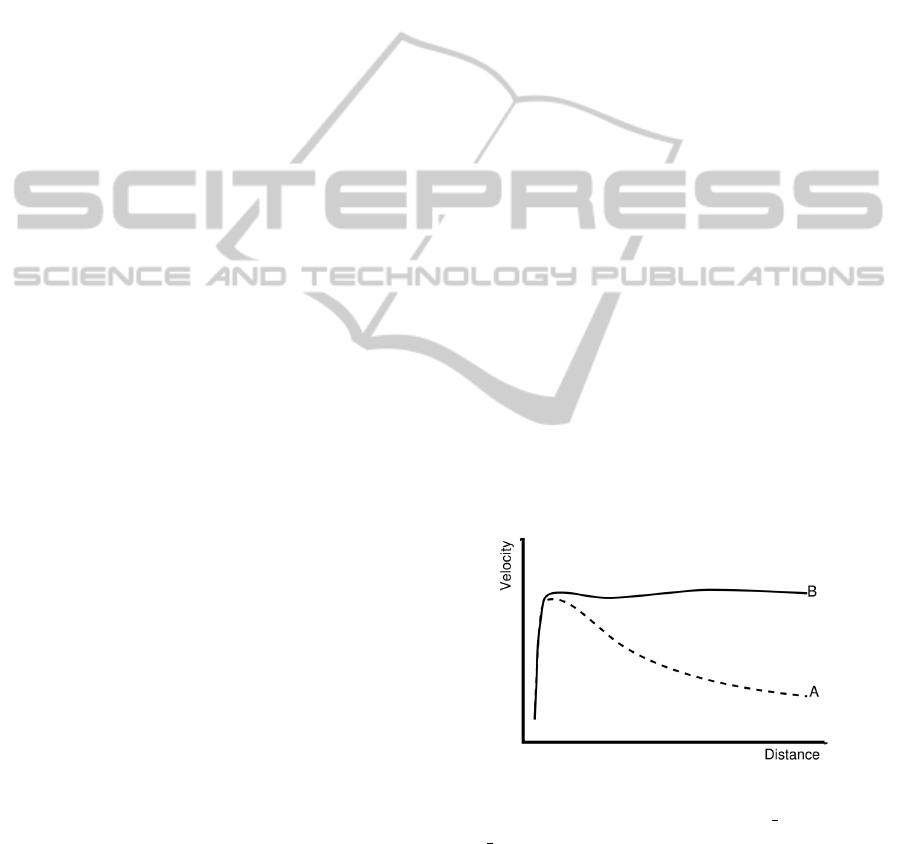
their radius. Figure 2 illustrates the predicted and ac-

tual graphs. In order to account for this discrepancy

it is hypothesed that galaxies contain an invisible halo

of, so called, dark matter which does not radiate and

can only be measured indirectly. Accordingly WMS

adds to the function that computes the stellar orbital

velocity a second component that depends on dark

matter.

This diagram is taken from

http://en.wikipedia.org/wiki/Galaxy rotation

problem. The x-axis is the radii of the stars

and the y-axis is their orbital velocities. The

dotted line (A) represents the predicted graph

and the solid line (B) is the actual graph that

is observed.

Figure 2: Predicted vs Observed Stellar Orbital Velocities.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

In the next sections we discuss how the physics

knowledge underlying these two cases can best be

represented in FOL and HOL, respectively, in order

for a HOL-theorem prover like Isabelle to diagnose

the contradiction between what is expected and what

is observed.

3 ONTOLOGICAL

REPRESENTATION OF

PHYSICS

The language physicists use for expressing relation-

ships between concepts is largely based on mathemat-

ics rather than on an expressive logic. It is one of

our contributions in this project to provide a logical

formalisation of physics formulae and historical ex-

amples of ontology evolution. As already mentioned,

the need for evolution arises when experimental ob-

servations contradict theoretical predictions; thus, to

formalise such situations, the predictive theory and

sensory data are encapsulated in separate ontologies,

which we call O

and O

respectively. Such modular

representation, though basic, provides a range of ben-

eﬁts, including better control of contradiction, more

focused effects of repair, variable certainty and in-

creased reusability. To further modularise the existing

knowledge representation, the physics and mathemat-

ical theories can be partitioned into small ontologies.

Each ontology resembles a small context, e.g., some

treatment of physics may depend on separate ontolo-

gies for a formal theory and for a naive theory of ge-

ometry, which only covers 2-D spaces. Certainty fac-

tors can be assigned to an ontology, determining the

vulnerability of the theory or experiment to repair. For

instance, the ontology of a controversial theory could

be valued at a lower conﬁdence than an established

one. The structure used for storing and managing

the ontologies should therefore be able to accommo-

date a sufﬁciently large collection of partitioned on-

tologies because even fundamental ontologies them-

selves, e.g., Newtonian Mechanics, arithmetic, etc.,

may be represented as a collection of smaller ontolo-

gies. That said, the structure should also support the

management of relations and dependencies between

ontologies and their terms.

3.1 Modular Representation as a

Development Graph

For the storage and management of the collection

of ontologies, we use a formal logical representation

called development graphs (Autexier et al., 1999), in

Figure 3: Development graph for the bouncing-ball para-

dox.

which nodes and links correspond to ontologies and

morphisms, respectively. A logical theory (in our

case, an ontology) is characterised by a node, which

can be deﬁned to import signatures and axioms from

other nodes via deﬁnitional links. As will be de-

scribed later, the ontologies are formalised as locales

(Ballarin, 2004) in Isabelle, which are mechanisms

for performing modular reasoning; each locale corre-

sponds to a node in the development graph. There are

also other types of morphisms implemented, the de-

tails of which are not covered in this paper. Develop-

ment graphs are not only useful for formalisation of

ontologies, but also for visualisation of the relations

between ontologies and the complete structure. De-

velopment graphs are already implemented in HETS

(Mossakowski et al., 2007), which is a system for the

analysis of various speciﬁcation languages.

3.1.1 Example Representation

To provide a visualisation of the structure of the on-

tologies for the model of the bouncing-ball para-

dox, Figure 3 depicts a development graph con-

taining the relevant ontologies (nodes) and deﬁni-

tional links (arcs); it is an illustration of the de-

velopment graph visualised in HETS. In this rep-

resentation, the top ontology BasicPhys contains

the fundamental concepts in physics, e.g., time and

events. It extends from OrderedReals, which is

an internal speciﬁcation of reals with ordering. The

node ClassicalEnergyConv contains types speciﬁc

to energy conversion, e.g., those for various types

of energy, including total energy, kinetic energy,

and potential energy, but not the theories describ-

HIGHER-ORDER REPRESENTATION AND REASONING FOR AUTOMATED ONTOLOGY EVOLUTION

ing the conversion between types of energy. Note

that it extends from BasicPhys, so all sorts (types)

and operations, if any, are directly imported. Fol-

lowing the path down, the node OtLaws contains

the theory of energy conversion for particles (with-

out extent) between kinetic and potential energies

for all objects and time moments, i.e. ∀o:Ob j,t :

Time. TE(o,t) = KE(o,t) + PE(o,t); that is, it pre-

dicts that potential energy can be converted to only

kinetic energy because elastic and other types of

energy are neglected. Moreover, it contains def-

initions as well, e.g., ∀o.Ob j,t.Time. KE(o,t) =

Mass(o,t).Vel(o,t)

. The theoretical ontology Ot

extends from OtLaws, which imports the same predic-

tive theory as that in OtLaws. In addition, it contains

axioms specifying that the initial velocity is zero and

the height is greater than zero. In contrast, the sen-

sory ontology Os extends from OsLaws, which itself

extends from ClassicalEnergyConv. OsLaws con-

tains similar axioms as OtLaws, but at a lower level of

generality. The axioms of OsLaws cover only the spe-

ciﬁc entities and events involved in the experiment,

e.g., T E(ball,End(drop)) = KE(ball,End(drop))+

PE(ball,End(drop)) which restricts the deﬁnition to

the particular ball being dropped and the particular

dropping event involved. Os, unlike Ot, contains ax-

ioms specifying that the ﬁnal height and velocity are

both zero.

The development graph of the dark matter exam-

ple exhibits a similar structure, so it is omitted to

avoid repetition.

3.2 Axiomatisations of Theoretical and

Sensory Ontologies

Representational choices need to be made regarding

the axiomatisations of O

and O

. The ontological

representation of the predictive theory as O

is rel-

atively straightforward as O

requires access to the

same physics laws as those needed in the case study,

which are encoded as axioms; the axioms are con-

tained in O

Law, but are exported to O

. As brieﬂy

described already, O

has access to the same axioma-

tised laws in O

, but with lesser generality; these are

contained in O

Law, but are exported to O

. Instead

of expressing the laws over the entire relevant do-

main, the domain of quantiﬁcation in O

is speciﬁc to

the entities involved in the experiment. Therefore, O

makes a lesser commitment than O

because it com-

mits itself only to the entities of the experiment. For

the bouncing-ball paradox, the axioms of the O

and

are:

Ax(O

) ::= {

∀p:Part,t

:Mom.TE(p,t

) = TE(p,t

∀p:Part,t:Mom. TE(p,t) = KE(p,t) + PE(p,t),

∀p:Part,t:Mom. KE(p,t) ::=

Mass(p,t).Vel(p,t)

∀p:Part,t:Mom. PE(p,t) ::= Mass(p,t).G.

Height(p,t)

}

Ax(O

) ::= {

TE(ball, End(drop)) = KE(ball,End(drop))+

PE(ball, End(drop)),

KE(ball, End(drop)) ::=

Mass(ball,End(drop)).

Vel(ball, End(drop))

PE(ball, End(drop)) ::= Mass(ball, End(drop)).G.

Height(ball, End(drop))

}

where TE(p,t), KE(p,t), and PE(p,t) respectively

denote the amount of total energy, kinetic energy, and

potential energy of an object p at a time moment t;

Mass(p,t) and Vel(p,t) respectively denote the mass

and velocity of p at t; G is the gravitational con-

stant; Start(drop) and End(drop) respectively denote

the start and end of the dropping of the ball.

For the dark matter case study, the axioms of O

and O

are:

Ax(O

) ::= {

∀o:Obj, g:Galaxy. AngVel(o, g) =

OrbVel(o, g)

Rad(o,g)

, (4)

∀o:Obj, g:Galaxy. Rad(o,g) > 0, (5)

∀o:Obj. GraphA(o) = (Rad(o, MWay), (6)

AngVel(o,MWay).Rad(o,MWay))

}

Ax(O

) ::= {

∀o:Obj. AngVel(o,MWay) =

OrbVel(o, MWay)

Rad(o,MWay)

(7)

∀o:Obj. Rad(o, MWay) > 0, (8)

∀o:Obj. GraphB(o) = (Rad(o, MWay), (9)

OrbVel(o, MWay))

}

where AngVel(o, g) and OrbVel(o,g) respectively de-

note the angular and orbital velocities of an object o in

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

the galaxy g; Rad(o,g) returns radius between o and

the centre of the galaxy g; and MWay is our galaxy,

Milky Way.

The representation of O

(and O

Laws) adopted

may appear ad-hoc as it requires O

to have access to

the same laws as O

but expressed at the lowest level

of generality. However, this reﬂects a situation where

the sensory data in O

is interpreted under the context

of the theory O

, so the data would be interpreted us-

ing the laws available in O

. The minimal exportation

of the theoretical laws, therefore, involves the same

laws but at the lowest level of generality. This inter-

pretation is analogous to a physicist’s making sense

of new sensory data in accordance to his/her current

physics theory and understanding of the initial exper-

iment setting. Of course, there are other alternative

representations that are worthy of further work, each

implying a different philosophy of the content of O

and of the set of deducible theorems:

(a) O

has access to the same axiomatised laws as

those imported by O

and have the same domain

of quantiﬁcation, so O

has access to the same

physics as O

. One shortcoming of this represen-

tation is the loss of distinction between predictive

theory and mere experimental evidence. Adopt-

ing such representation is equivalent to modelling

the evolution of a physicist’s ontological under-

standing of physics when confronted by two con-

ﬂicting sets of data.

(b) O

shares only the language of O

and does not

import any physics laws and deﬁnitions, so O

is a knowledgebase. In order to derive a contra-

diction between the two ontologies without los-

ing the distinction between them, the reasoning

mechanism must then be able to access both O

’s

and O

’s axioms. This is more general than those

described above because, in an environment in

which there are multiple theoretical ontologies

confronting the same O

, the deducible theorems

then depend on the axioms of the particular theo-

retical ontology.

is not committed to share the language or the

axioms of O

, so this is the most general repre-

sentation. The terms in O

and O

still need to

be related in order to perform reasoning. One

approach is to introduce metal-level relations be-

tween terms across the two ontologies, perceiving

each as a different context (McCarthy and Buvac,

1998). The reasoning mechanism needs to ac-

count for both the meta-level relations between

terms and object-level formulation, which signif-

icantly increases the complexity of the task.

Undoubtedly, representation (c) is the most interest-

ing avenue given the potentially high level of exten-

sibility and generality. It is similar to the current

representation in the way that both address the need

for interpretation of the data in O

in the context of

. However, the required axioms for contextual rea-

soning in the current representation are explicitly en-

coded in OsLaws at the object-level, which can han-

dle only O

, whereas in (c) these may be represented

at the meta-level, which can handle multiple, arbitrary

contexts. That said, we believe the representation we

have currently adopted strikes a reasonable balance

between expressivity and complexity.

4 REASONING FOR

AUTOMATED ONTOLOGY

EVOLUTION

The initial reasoning step for ontology evolution is to

determine whether a conﬂict exists between the on-

tologies and which ontology repair plan should be

triggered. Without a robust and correct reasoning

mechanism, a repair plan could be triggered to mod-

ify an already correct ontology or might not be trig-

gered when it is supposed to be: giving rise to false-

positives and false-negatives, respectively. Using the

representation described previously in §3, the diag-

nosis can take place by translating nodes into logical

theories in the logic of a particular theorem prover and

then attempting to deduce trigger formulae in those

theories.

4.1 Detection of Conﬂicts between

Ontologies

If we reason with an inconsistent ontology, then every

formula is deducible in multiple ways, leading to an

explosion of provable theorems. Therefore, when we

prove whether a trigger formula is a theorem of some

given ontologies to detect a conﬂict between them, the

ontologies cannot be ﬁrst merged.

For reasoning in both ﬁrst-order and higher-order

logics, we use the interactive theorem prover Isabelle

because its emphasis on proving higher-order theo-

rems. Isabelle, although powerful, does not offer tools

tailored for reasoning with modular ontologies. For-

tunately, there are at least two workarounds for rea-

soning modularly without reverting to merging the ax-

ioms of the ontologies and giving rise to an inconsis-

tent set of axioms. One is to specify the ontologies

as separate Isabelle theories and another is to specify

them as separate locales (Ballarin, 2004), which are

mechanisms for deﬁning local scopes in a proof. The

HIGHER-ORDER REPRESENTATION AND REASONING FOR AUTOMATED ONTOLOGY EVOLUTION

locales approach is more attractive because each of

our ontologies can be viewed as an individual context

and theorems can be proved in the context of a spec-

iﬁed locale. That said, each locale corresponds to a

node in a development graph as each node represents

an ontology, which is analogous to a context. In this

section, we present the procedure for the diagnosis

of conﬂict in the bouncing-ball and dark matter case

studies. The type of conﬂict under scrutiny is that for-

malised in the WMS ontology repair plan (Bundy and

Chan, 2008), of which the trigger is speciﬁed in Fig-

ure 1. Note that some parts of the proofs are been

omitted due to space limitations.

4.1.1 By First-order Proof Calculus

To trigger WMS in the bouncing-ball paradox pre-

sented earlier, we need to show that (1), (2), and (3)

are deducible. The trigger formulae can be instanti-

ated with the following substitution:

{TE/stuff , hball,End(drop)i/

TE(ball, Start(drop))/v

,0/v

}

With this substitution, the instantiated form of (1), (2),

and (3) is:

` TE(ball, End(drop)) = (10)

TE(ball, Start(drop))

` TE(ball, End(drop)) = 0 (11)

` TE(ball, Start(drop)) 6= 0 (12)

where, in physics terms, (12) comes from the initial

condition that the ball is suspended from a positive

height, (10) comes from the law of conservation of

energy so that the total amount of energy at the start

and at the end of the drop should be the same, and (11)

is deduced from the observation that at the end of the

drop both the velocity and the height of the ball are

zero. The representation of the paradox does not re-

quire quantiﬁcation over functions, so ﬁrst-order logic

is sufﬁcient for the representation. To prove the trig-

ger formulae in this example, HOL is therefore used

to reason over FOL, as demonstrated in the Isabelle

proof below:

typedecl Obj

typedecl Event

types Energy = real Time = real

A constant for representing the ball

consts ball :: Obj

Each of the ontologies outlined in Figure 3 is spec-

iﬁed as a locale. Locale BasicPhys corresponds to

a::τ denotes that a is of type τ.

the node BasicPhys in Figure 3, which represents an

ontology specifying the language of O

and O

locale BasicPhys =

ﬁxes Vel :: "Obj ⇒ Time ⇒ real"

and Height :: "Obj ⇒ Time ⇒ real"

and Start :: "Event ⇒ Time ⇒ real"

...

The locale ClassicalEnergyConv corresponds

to the node ClassicalEnergyConv in the devel-

opment graph, which imports the signature from

BasicPhys and extends it with a language for rep-

resenting various types of energies:

locale ClassicalEnergyConv =

ﬁxes TE :: "Obj ⇒ Time ⇒ real"

and KE :: "Obj ⇒ Time ⇒ real"

and PE :: "Event ⇒ Time ⇒ Energy"

...

Locale OtLaws corresponds to the node OtLaws

in the development graph and contains the axioms

constituting the deﬁnitions of total energy (without

elasticity), potential energy, kinetic energy, the law

of conservation of energy, and the gravitational con-

stant

locale OtLaws = BasicPhys +

assumes te: "TE p t = PE p t + KE p t"

and pe: "PE p t = Mass p×G×Height p

and ke: "KE p t = 0.5×Mass p×Vel p

t×Vel p t"

...

Locale Ot corresponds to Ot and asserts the values

of the initial velocity, initial height, and mass of the

ball:

locale Ot = OtLaws +

assumes vinit: "Vel ball (Start drop)

= 0"

and hinit: "Height ball (Start drop)

> 0"

and mass: "Mass ball > 0"

Locale OsLaws corresponds to the node OsLaws

and represents an ontology containing axioms based

on the laws over a speciﬁc domain:

locale OsLaws = BasicPhys +

assumes te: "TE p t = PE p t + KE p t"

and pe: "PE p t = Mass p×G×Height p

and ke: "KE p t = 0.5×Mass p×Vel p

t×Vel p t"

...

The locale Os corresponds to Os and asserts the

values obtained from observation, i.e. the ﬁnal values

of the velocity, height, and mass of the ball:

If F is a function, F x denotes the application of F to x.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

locale Os = OsLaws +

assumes vfin: "Vel ball (End drop) =

and hfin: "Height ball (End drop) =

and mass: "Mass ball > 0"

To prove the trigger formulae in Figure 1, we need

to be able to deduce the total amount of energy from

basic quantities, e.g., velocity, height and mass. Is-

abelle has a rich library of mathematical theorems,

which signiﬁcantly helps the rewriting of equations

and the substitution of values. Three theorems are

needed to be proven in the ontologies: one proposes

that there exists a moment when the ﬁnal amount of

total energy is equal to the initial amount of total en-

ergy, the ﬁnal amount of total energy is zero, and the

initial amount of total energy is not zero. Hence, the

ﬁrst proof goal to be discharged is (1), which can be

proved using the instantiation (10):

lemma (in Ot) lem1: "TE ball (End drop)

= TE ball (Start drop)"

using cons by auto

theorem (in Ot) OtWMS1: "EX (stuff::?’a

⇒ ?’b) s v1. stuff s = v1"

proof (intro exI) qed (rule lem1)

The second proof goal to be discharged is (2),

which can be proved using the instantiation (11):

lemma (in Os) lem2: "TE ball (End drop)

= 0"

using mass vfin hfin te ke pe g

by auto

theorem (in Os) OsWMS1: "EX

(stuff::?’a=>?’b) s v2. stuff s = v2"

proof (intro exI) qed (rule lem2)

The ﬁnal proof goal to be discharged is (3), which

can be proved using the instantiation (12):

theorem (in Ot) OtWMS2: "TE ball (Start

drop) 6= 0"

proof ... qed

4.1.2 By Higher-order Proof Calculus

The proposed existence of dark matter is a case study

which requires a higher-order representation. As de-

scribed earlier, since the two graphs in Figure 2 are

compared, function objects can be used to represent

graphs in the formulation. Formulae (1), (2), and (3)

can be instantiated with the following substitution:

{λs ∈ g. hRad(s),OrbVel(s)i/stuff ,

hMWayi/

s, Graph

, Graph

}

which gives the instantiated form of the trigger for-

mulae as follows:

` λs ∈ MWay. hRad(s), (13)

OrbVel(s)i = Graph

` λs ∈ MWay. hRad(s), (14)

OrbVel(s)i = Graph

` Graph

6= Graph

(15)

where OrbVel(s) is the orbital velocity of star s,

Rad(s) is the radius of s from the centre of the Milky

Way, and MWay is our own galaxy, represented as the

set of stars it contains. Formula (14) shows the pre-

dicted graph, Graph

: the orbital velocity decreases

roughly inversely with the square root of the radius

(see Figure 2). This graph is deduced by Newtonian

Mechanics from the observed distribution of the vis-

ible stars in the Milky Way. Formula (15) shows the

actual observed orbital velocity graph, Graph

: it is

almost a constant function over most of the values of s

(see Figure 2). Note the use of λ-abstraction to create

graph objects as unary functions. These two graphs

are unequal (15), within the range of legitimate ex-

perimental variation.

The following proof illustrates the power of using

Isabelle’s higher-order proof calculus to detect a con-

ﬂict between the two HOL ontologies, which exhibits

a similar structure to the previous proof:

typedecl Obj

types Spiral = "Obj set" Time = real

A constant for representing the Milky Way:

consts MWay :: Spiral

Locale BasicPhys corresponds to BasicPhys in

the development graph, which represents the ontology

containing only the language of locales O

and O

this particular case study:

locale BasicPhys =

ﬁxes OrbVel :: "Obj => Obj set ⇒

real"

and GrphP :: "Obj ⇒ real×real"

...

assumes cab: "∃ P. P 6= {} ∧ (∀x. x∈P

−→ CurveA x 6= CurveB x)"

and gcp: "GrphP = CurveP"

and gca: "GrphA = CurveA"

locale OtLaws = BasicPhys +

assumes radgtzero: "Rad p g > 0"

and ovabsov: "OrbVel p g = abs

(OrbVel p g)"

Locale Ot contains the deﬁntion of angular veloc-

ity in terms of orbital velocity. it also asserts that its

graph is a plot of the product of angular velocity by

radius:

HIGHER-ORDER REPRESENTATION AND REASONING FOR AUTOMATED ONTOLOGY EVOLUTION

locale Ot = OtLaws +

assumes avel: "AngVel p g = OrbVel p g

/ Rad p g"

and ga: "GrphP p = (Rad p MWay,

AngVel p MWay × Rad p MWay)"

locale OsLaws = BasicPhys +

assumes radgtzero: "∀ p. p∈MWay −→ Rad

p MWay > 0"

and ovabsov: "∀ p. p∈MWay −→ OrbVel p

MWay = abs (OrbVel p MWay)"

Locale Os explicitly asserts that its graph is a plot

of the orbital velocity of stars in the Milky Way.

locale Os = OsLaws +

assumes gb: "GrphA p = (Rad p MWay,

OrbVel p MWay)"

Similar to the previous proof, the ﬁrst proof goal

to be discharged here is (1), which can be proved us-

ing the instantiation (14):

lemma (in Ot) lem1: "(λ g s. (Rad s g,

OrbVel s g)) MWay = GrphP"

apply (simp add: expand_fun_eq)

...

theorem (in Ot) OtWMS1: "∃(stuff::?’a ⇒

?’b) s v1. stuff s = v1"

proof (intro exI) qed (rule lem1)

The second proof goal to be discharged is (2),

which can be proved using the instantiation (15):

lemma (in Os) lem2: "(λ g s. (Rad s g,

OrbVel s g)) MWay = GrphA"

using gb

by (simp add: expand_fun_eq)

theorem (in Os) OsWMS1: "∃(stuff::?’a ⇒

?’b) s v2. stuff s = v2"

proof (intro exI) qed (rule lem2)

The ﬁnal proof goal to be discharged is (3), which

can be proved using the instantiation (15):

theorem (in Ot) OtWMS2: "GrphA 6= GrphP"

using cab gca gcp by auto

5 DISCUSSION

The two case studies presented have shown the bene-

ﬁts of representing the predictive theory and the sen-

sory data as separate ontologies. By encoding each

ontology as an individual locale that is locally consis-

tent, each of the three parts of the WMS trigger formu-

lae is simply an open theorem of the relevant ontol-

ogy. If the two were merged, then there would be an

explosion of uninteresting theorems. Moreover, the

case studies have demonstrated the need for higher-

order logic and the power of using a higher-order the-

orem prover such as Isabelle for aiding automated on-

tology evolution. For example, Isabelle’s polymor-

phic meta-logic is particularly useful for the detection

of the trigger formula because stuff has a polymorphic

type a ⇒ b and, before diagnosis, how it is to be in-

stantiated is not known. An obvious advantage is that

the type of stuff is a variable, which provides a sufﬁ-

ciently high level of generality in the trigger formula.

As shown in the proof for the bouncing-ball paradox,

stuff is instantiated by TE with type Ob j ⇒ Time ⇒

real, whereas in that for the existence of dark mat-

ter, stuff is instantiated by λs t.hRadius s t,Orb s ti

with type Ob j ⇒ real × real. Moreover, the proof of

the trigger formula (2) requires the comparision using

the equality and the inequality operators, which are

polymorphic as well. For example, real numbers and

functions are compared in the bouncing-ball and the

dark matter case studies respectively, so the operators

have deﬁned meanings on reals in one scenario and

on functions in another.

On the representational aspect, if a less expressive

logic, e.g., DL or FOL, was adopted, it would be im-

possible to reason over function objects. Signiﬁcant

changes to the representation would be required in or-

der to perform the described kind of reasoning. For

example, in the dark matter case study, the represen-

tation of the function of the orbit of a star could no

longer be a functional object, but a (possibly inﬁnite)

set of positional points in a 3-D space, which we be-

lieve is unnatural.

6 CONCLUSIONS

Further progress in handling automated ontology evo-

lution is now urgent, due to the demand created by

multi-agent systems. We have outlined two main

challenges to the development of mechanisms sup-

porting automated ontology evolution, i.e. designing

a modular representation and performing reasoning

across modular ontologies. The latter imposes a rela-

tively greater challenge in our domain as it demands

an unusual use of higher-order theorem proving with

interactive provers. As described, a formal logical

structure is adopted to store and manage ontologies

and ontologies themselves are treated as expressive

logical theories. Evident by the two described exam-

ples from physics, our work is showing the advan-

tages of the unusual use of Isabelle for higher-order

reasoning with modular ontologies and the visualisa-

tion of the structure as a development graph.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

ACKNOWLEDGEMENTS

The research reported in this paper was supported by

EPSRC grant EP/E005713/1.

REFERENCES

Autexier, S., Hutter, D., Mantel, H., and Schairer, A.

(1999). Towards an Evolutionary Formal Software-

Development Using CASL. Lecture Notes In Com-

puter Science; Vol. 1827, pages 73–88.

Ballarin, C. (2004). Locales and locale expressions in

Isabelle/Isar. Lecture Notes in Computer Science,

3085:34–50.

Bundy, A. and Chan, M. (2008). Towards ontology evolu-

tion in physics. In Hodges, W., editor, Procs. Wollic

2008. LNCS, Springer-Verlag.

Bundy, A., J., L., Qi, G., and Varzinczak, I. (2009). Notes of

the ijcai-09 workshop on automated reasoning about

context and ontology evolution. AAAI Press.

Chan, M. and Bundy, A. (2008). Inconstancy: An on-

tology repair plan for adding hidden variables. In

Bringsjord, S. and Shilliday, A., editors, Symposium

on Automated Scientiﬁc Discovery, number FS-08-03

in Technical Report, pages 10–17. AAAI Press. ISBN

978-1-57735-395-9.

diSessa, A. (1983). Phenomenology and the evolution of in-

tuition. In Stevens, A. and Gentner, D., editors, Men-

tal Models, pages 15–33. Erlbaum.

Doan, A., Madhavan, J., Domingos, P., and Halevy, A.

(2004). Ontology matching: A machine learning ap-

proach. Handbook on Ontologies in Information Sys-

tems, pages 397–416.

Ghilardi, S., Lutz, C., and Wolter, F. (2006). Did I damage

my ontology? A case for conservative extensions in

description logic. Proceedings of the Tenth Interna-

tional Conference on Principles of Knowledge Repre-

sentation and Reasoning (KR-2006), pages 187–197.

Giunchiglia, F. and Shvaiko, P. (2004). Semantic matching.

The Knowledge Engineering Review, 18(03):265–

280.

Kalfoglou, Y. and Schorlemmer, M. (2003). Ontology map-

ping: the state of the art. The Knowledge Engineering

Review, 18(1):1–31.

Kalyanpur, A., Parsia, B., Sirin, E., and Grau, B. (2006).

Repairing unsatisﬁable concepts in OWL ontologies.

In ESWC, pages 170–184. Springer.

Lam, J., Sleeman, D., Pan, J., and Vasconcelos, W. (2008).

A ﬁne-grained approach to resolving unsatisﬁable

ontologies. Lecture Notes in Computer Science,

4900:62.

McCarthy, J. and Buvac, S. (1998). Formalizing con-

text (expanded notes). Computing natural language,

81:13–50.

McNeill, F. and Bundy, A. (2007). Dynamic, automatic,

ﬁrst-order ontology repair by diagnosis of failed plan

execution. International Journal On Semantic Web

and Information Systems, 3(3):1–35. Special issue on

ontology matching.

Mossakowski, T., Maeder, C., and L

uttich, K. (2007). The

Heterogeneous Tool Set. In Grumberg, O. and Huth,

M., editors, TACAS 2007, volume 4424 of Lecture

Notes in Computer Science, pages 519–522. Springer-

Verlag Heidelberg.

Ovchinnikova, E. and K

uhnberger, K. (2007). Auto-

matic Ontology Extension: Resolving Inconsisten-

cies. OTT’06, 1:93.

Paulson, L. C. (1994). Isabelle: A generic theorem prover.

Springer-Verlag.

Stojanovic, L., Maedche, A., Motik, B., and Stojanovic,

N. (2002). User-Driven Ontology Evolution Man-

agement. In Proceedings of the 13th International

Conference on Knowledge Engineering and Knowl-

edge Management. Ontologies and the Semantic Web,

pages 285–300. Springer-Verlag London, UK.

HIGHER-ORDER REPRESENTATION AND REASONING FOR AUTOMATED ONTOLOGY EVOLUTION